Relationship between Evapotranspiration and Land Surface Temperature under Energy- and Water-Limited Conditions in Dry and Cold Climates
Abstract
Remotely sensed land surface temperature- (LST-) dependent evapotranspiration (ET) models and vegetation index- (VI-) LST methods may not be suitable for ET estimation in energy-limited cold areas. In this study, the relationship of ET to LST was simulated using the process-based Simultaneous Heat and Water (SHAW) model for energy- and water-limited conditions in Mongolia, to understand the differences in ET processes under these two limiting conditions in dry and cold climates. Simulation results from the SHAW model along with ground observational data showed that ET and LST have a positive relationship when air temperature (Ta) is less than or equal to the temperature (Ttra) above which plants transpire and have a negative relationship when Ta is greater than Ttra under the energy-limited condition. However, ET and LST maintain a negative relationship with changes in Ta under the water-limited condition. The differences in the relationship between ET and LST under the energy-limited and water-limited conditions could be attributed to plant transpiration and energy storage in moist/watered soil and plants. This study suggests that different strategies should be used to estimate ET under the energy-limited condition in dry and cold climates.
1. Introduction
Terrestrial evapotranspiration (ET), defined as the loss of water from the land surface to the atmosphere, is a key process in water cycles [1, 2]. ET closely relates to greenhouse gas efflux and production [3], plant growth [4–6], and droughts [7, 8]. Therefore, it is essential to understand the ET phenomenon over wide ranges of space and time for water resources management and climate change studies.
Regional or global ET maps are often obtained through satellite remote sensing [9, 10]. Among remote sensing-based ET estimation methods, remotely sensed land surface temperature- (LST) dependent methods, such as the vegetation index (VI) and LST scattered plot (VI-LST), and models that calculate ET as a residual of the land surface energy balance equation have been widely used. The LST-dependent ET models include SEBAL (remote sensing Surface Energy Balance Algorithm for Land) [11], Sim-ReSET (Simple Remote Sensing EvapoTranspiration model) [9], SEBI (Surface Energy Balance Index) and S-SEBI (Simplified-SEBI) [12], SEBS (Surface Energy Balance System) [13], and METRIC (Mapping EvapoTranspiration at high Resolution with Internalized Calibration) [14, 15], among others. The VI-LST methods use the VI-LST triangle/trapezoidal feature space to derive an index, and this index is used to partition sensible heat and latent heat fluxes from available energy (net radiation minus soil heat flux) [16–19]. Both LST-dependent ET models and VI-LST methods assume that ET can cool land surfaces under the condition of homogeneous atmospheric forcing. In other words, land surfaces with larger ET have lower LST while air temperature (Ta), air humidity, wind speed, and solar radiation remain homogeneous over land surfaces of interest. However, this assumption may be invalid in high latitudes (>50°) and cold areas [2], where ET commonly exhibits a positive relationship with LST [2, 20]. A positive relationship between LST and VI has also been observed in Alaska tundra ecosystems [21] and in North America above 45°N [22]. These findings indicate that both LST-dependent ET models and VI-LST methods may not be suitable for ET estimation in the energy-limited cold areas. A study to estimate water deficit (defined as the ratio of actual to potential ET) using the VI-LST method in southern Spain also suggests that the VI-LST method should not be used to calculate ET under energy-limited conditions [19].
Reasons for the incompetence of LST-dependent ET models and VI-LST methods in energy-limited cold areas have been seldom investigated so far. In this study, the relationship between ET and LST was investigated using the process-based Simultaneous Heat and Water (SHAW) model for energy- and water-limited conditions in Mongolia, to understand the difference in ET processes under such limiting conditions in dry and cold climates.
2. Methodology
2.1. SHAW Model
The Simultaneous Heat and Water (SHAW) model, a one-dimensional model that simulates heat, water, and solute transfer within the atmosphere-plant-soil system, was used to simulate ET and LST in this study. The SHAW model, developed by USDA Agricultural Research Service, has a detailed solution to simulate soil freezing and thawing and a sophisticated approach to simulate transpiration from a plant canopy and evaporation from soil [23, 24]. The SHAW model has been documented that it is capable to simulate heat and water movement through plant cover, snow, residue, and soil for investigating climate and anthropogenic effects on soil freezing, snowmelt, runoff, soil temperature, water, evaporation, and transpiration [23, 24]. Therefore, the calibrated SHAW model could be competent at numerically simulating the relationship between ET and LST.
Vegetation, climate, and soil data are required to run the SHAW model. These inputs include initial conditions for snow, soil temperature, and water content profiles; daily or hourly weather data; and parameters describing the vegetative cover, snow, residue, and soil. General site information is also needed to initialize the model, including the slope, aspect, latitude, and surface roughness parameters. Detailed information on these input parameters is listed in Table 1.
| Date type | Data item | Unit | Data source |
|---|---|---|---|
| Weather data | Air temperature | °C | AMS |
| Air humidity | % | AMS | |
| Precipitation | Inch | AMS | |
| Wind speed | mph | AMS | |
| Solar radiation | W/m2 | AMS | |
| Soil data | Bulk density | kg/m3 | Soil sample |
| Organic matter | % | Soil sample | |
| Sand | % | Soil sample | |
| Silt | % | Soil sample | |
| Clay | % | Soil sample | |
| Soil temperature | °C | AMS | |
| Soil moisture | m3/m3 | AMS | |
| Vegetation data | Vegetation canopy height | m | Vegetation sample |
| Dry matter | kg/m2 | Vegetation sample | |
| Leaf area index | — | Vegetation sample | |
| Root depth | m | Vegetation sample | |
| General site information | Slope | % | Field survey |
| Aspect | Degree | Field survey | |
| Latitude | Degree | GPS | |
| Elevation | m | GPS | |
2.2. Data
Weather Data. Hourly air temperature (Ta), wind speed, air humidity, precipitation, and solar radiation data were collected from an auto-meteorological station (AMS; 47.75°N 107.33°E) located near Ulaanbaatar in Mongolia. A dry and cold climate dominates the region around the AMS, with an annual mean air temperature of −2.8°C and annual total precipitation of 260 mm. Detailed information regarding the AMS can be found in Sun et al. [25].
Soil Data. Data for organic matter content, bulk density, and soil component ratio of sand, silt, and clay were obtained from soil samples that were analyzed in the lab. Soil temperature and moisture profile data were obtained from the AMS.
Vegetation Data. Grass height, dry matter, leaf area index (LAI), and root depth data were obtained by measuring grass samples.
2.3. Strategies for ET and LST Simulations
In this study, nine scenarios of Ta and four scenarios of topsoil water content (SWC, 0–25 cm) were combined to simulate ET and LST for energy- and water-limited conditions. Ta was set at −1–15°C to match the local cold climate, and SWC was set at 0.1–0.4 to cover the soil moisture range from dry to wet. Combinations of Ta and SWC could thereby simulate a wide range of energy and water conditions under which ET and LST are simulated using the SHAW model (Figure 1). The scenario of SWC = 0.1 represents the water-limited condition where ET is mainly limited by soil water shortage. The scenario of SWC = 0.4 with low Ta values represents the energy-limited condition where ET is mainly limited by low incoming solar radiation. Since low incoming solar radiation leads to low Ta, the proxy of low Ta along with saturated soil water content could be used to define the energy-limited condition. One combination of Ta and SWC along with other inputs was used to run the model. For each model run, the SWC data were used to initialize the moisture condition for the soil layer of 0–25 cm, and Ta data along with other weather data representing typical weather conditions at the AMS site in early spring were selected from the AMS dataset. A typical record of Ta and other weather data was repeated 84 times to simulate the condition of homogeneous atmospheric forcing. Therefore, ET and LST values from each run of the SHAW model represent the water and heat conditions of land surfaces under homogeneous atmospheric forcing. Outputted ET and LST values were plotted and analyzed using the linear regression method, and the slope and coefficient of determination (R2) of the linear regression were used to understand the relationship of ET to LST under different energy and moisture conditions.
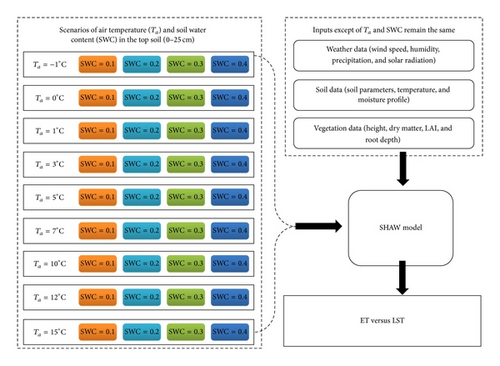
Before numerical simulations, intensive daily observational data during the period of August 2008 to August 2013 were used to calibrate the SHAW model by forcing the simulated soil temperature and water content to be consistent with observed values, respectively.
3. Results and Discussion
When the SHAW model was calibrated, simulations of nine scenarios of Ta (−1 to 15°C) and four scenarios of topsoil water content (SWC = 0.1, 0.2, 0.3, and 0.4) were conducted to estimate ET and LST. For each Ta scenario, the relationship of ET and LST for SWC = 0.2, 0.3, and 0.4 is similar, but for SWC = 0.1 the relationship is quite different. Below are detailed results and discussion regarding model calibration and the relationship of ET and LST under energy- and water-limited conditions.
3.1. Calibration Results for the SHAW Model
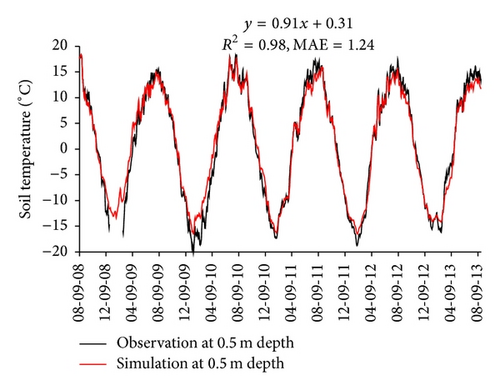
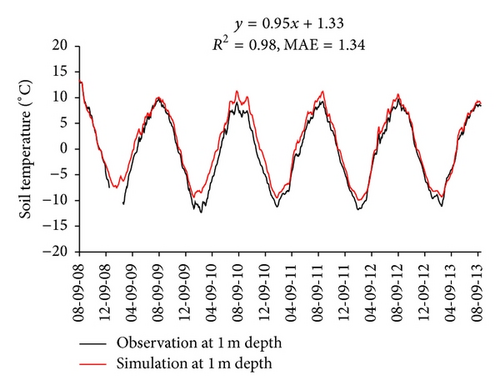
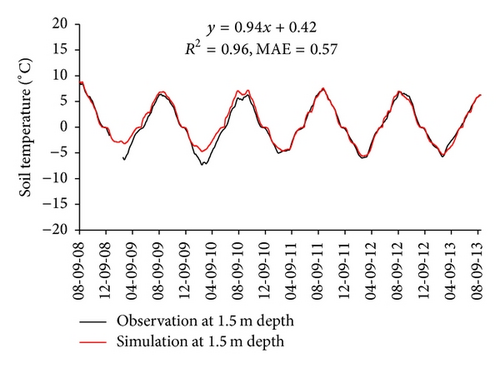
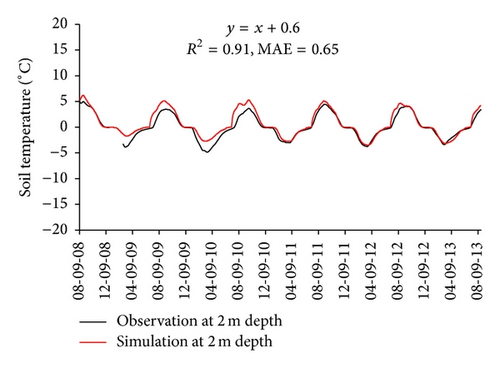
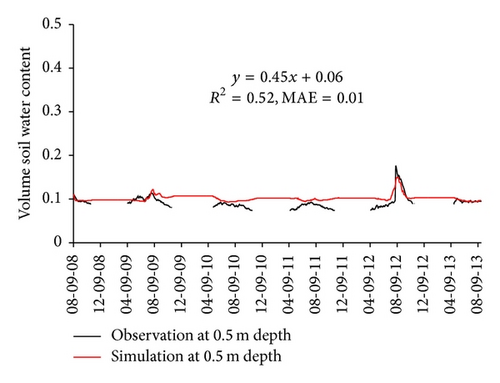
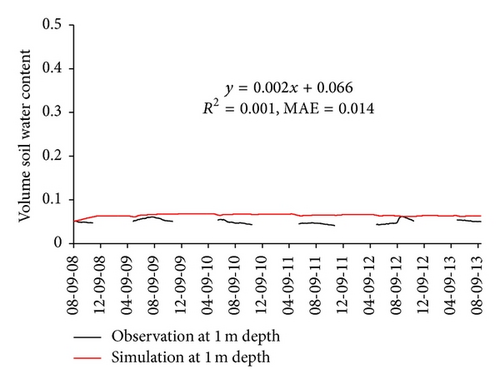
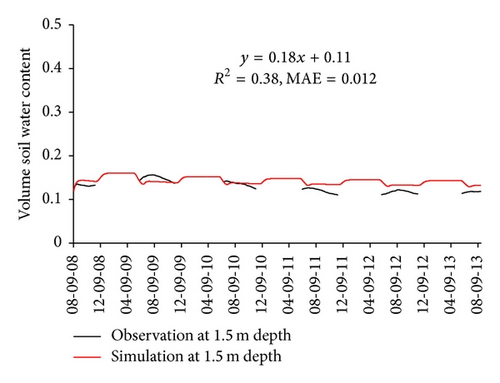
The comparison of simulated soil temperature and soil water content against observed values at four depths was used to evaluate the performance of the calibrated SHAW model. Figure 2 shows that simulated soil temperature matches observed one well in magnitude and seasonal variation. A linear analysis was conducted for each comparison. The coefficient of determination (R2) is greater than 0.9, and the mean absolute error (MAE) is less than 1.4°C at four depths. Figure 3 shows that simulated soil water content also matches observed one well in magnitude. The mean absolute error (MAE) is less than 0.015 at four depths. The simulated soil water content can capture the soil water recharge from precipitation as shown in Figure 3(a). Soil temperature and soil water content are two key variables of water and thermal processes in soil. Therefore, the consistence of soil temperature and soil water content between simulated and observed values could indicate that the calibrated SHAW model could perform well to investigate the relationship of ET and LST.
3.2. Relationship of ET and LST under the Energy-Limited Condition in a Cold and Dry Climate
The relationship of ET and LST under the soil moisture condition of SWC = 0.4 exhibited two patterns for nine simulations when Ta varied from −1 to 15°C. As shown in Figure 4, simulations with Ta from −1 to 5°C show that ET increases as LST increases, but this trend becomes progressively weaker with increases in Ta. The slope of linear regression analysis gradually decreases from 0.0059 to 0.0037, and the value of R2 also decreases from 0.8356 to 0.1153. The relationship of ET and LST abruptly changes at Ta = 7°C, and the slope of linear regression analysis becomes −0.0329 (R2 = 0.1525). This negative trend becomes stronger as Ta increases from 7°C to 15°C; the slope of linear regression analysis decreases from −0.0329 to −0.0636, and the value of R2 increases from 0.1525 to 0.2946.
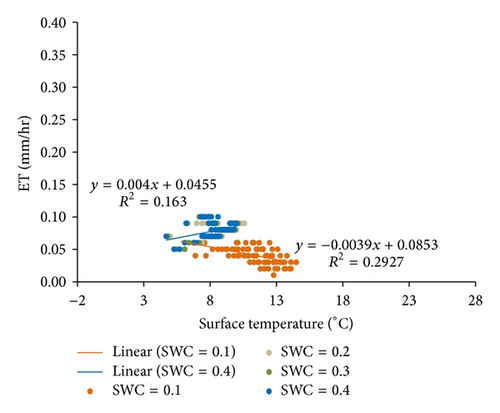
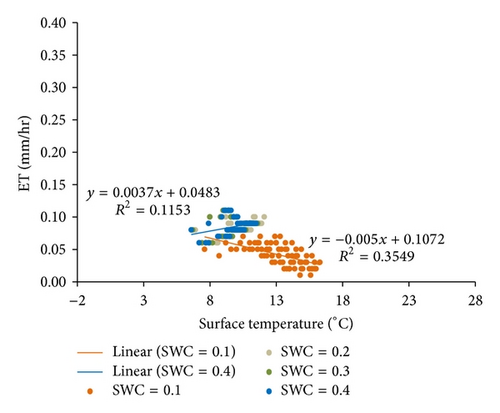
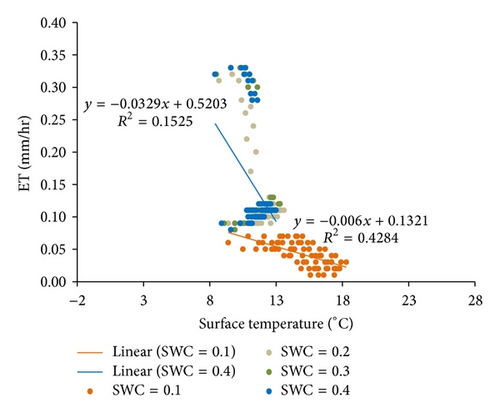
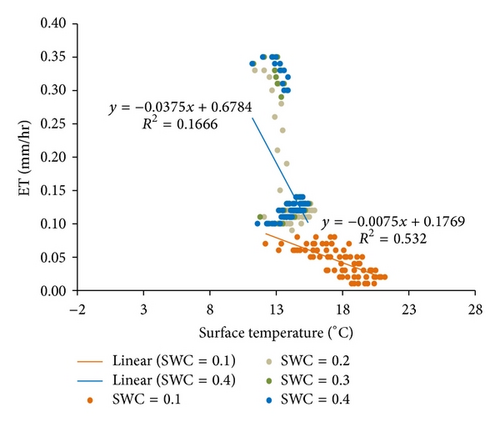
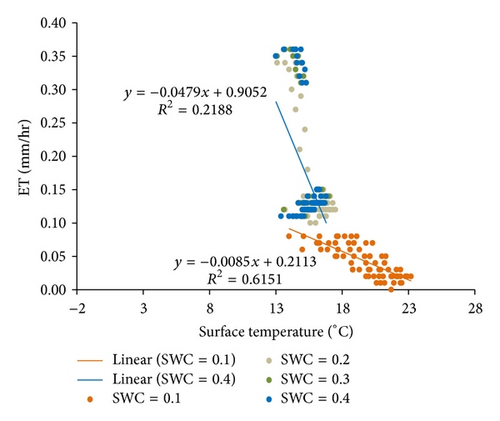
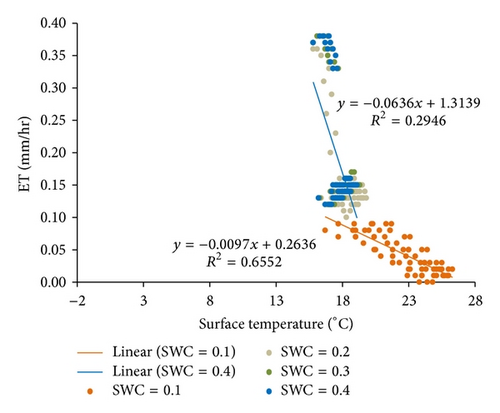
Figures 4(a)–4(e) show that higher land surface temperature enhances ET when air is cold (Ta ≤ 5°C) and soil water is not limited. These results suggest that some caution should be noted when ET is estimated from LST-dependent ET models and VI-LST methods. These methods for ET estimation assume that ET cools terrestrial surfaces through vegetation transpiration and soil (or water surface) evaporation and that moist/watered surfaces have relatively low values of LST. However, these assumptions are invalid under the energy-limited condition (Ta ≤ 5°C, SWC = 0.4).
3.3. Relationship of ET and LST under the Water-Limited Condition in a Cold and Dry Climate
Compared with the energy-limited condition, the relationship of ET and LST under the water-limited condition (SWC = 0.1) is relatively straightforward. As shown in Figure 4, the trend of decreasing ET with increasing LST becomes more distinct as Ta is increased from −1 to 15°C. The slope of linear regression analysis gradually decreases from −0.0022 to −0.0097, and the value of R2 increases from 0.1323 to 0.6552. Results from Figure 4 indicate that ET has an apparent cooling effect even when Ta is less than or equal to 5°C under the water-limited condition (SWC = 0.1). Under such a condition, the assumption of ET cooling appears to be valid, and ET can be estimated from LST-dependent ET models and VI-LST methods.
3.4. Effect of Plant Transpiration on the Relationship of ET and LST under the Energy- and Water-Limited Conditions in a Cold and Dry Climate
Plant transpiration has a clear impact on the relationship of ET and LST under the energy-limited condition. As shown in Figure 5, the relationship of ET and LST becomes negative when Ta is greater than 5°C, which for this study was set as the temperature above which plants start to transpire. It indicates that soil evaporation has no clear cooling function when Ta ≤ 5°C, whereas plant transpiration above 5°C can cool land surfaces under the energy-limited condition.
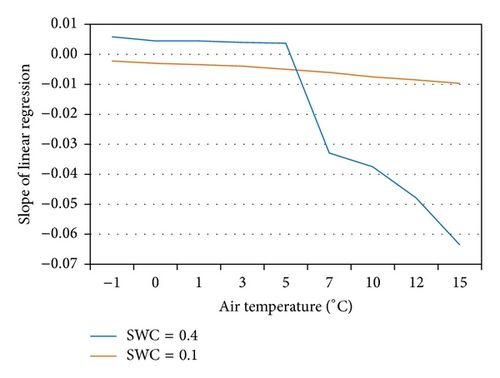
Plant transpiration has less impact on the relationship of ET and LST under the water-limited condition. As shown in Figure 5, the relationship of ET and LST remains negative under the water-limited condition, and this negative relationship becomes more pronounced when Ta > 5°C (Figure 6). This indicates that soil evaporation has a cooling function even when Ta ≤ 5°C and that plant transpiration above 5°C can enhance the cooling effect under the energy-limited condition.
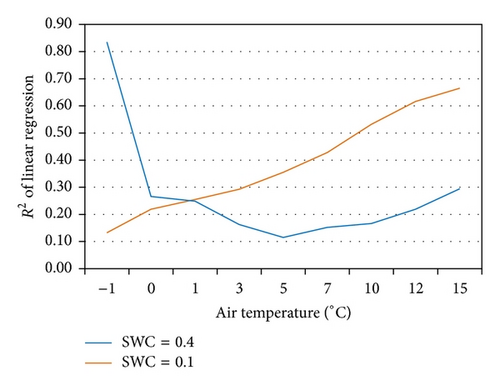
Summarizing the inferences drawn from Figures 5 and 6, plant transpiration shows a cooling effect under both energy- and water-limited conditions, while soil evaporation has a cooling effect under the water-limited condition only. These results suggest that care should be taken with ET estimation from LST-dependent ET models and VI-LST methods at temperatures below which plants do not transpire (Ta ≤ 5°C in this study).
3.5. Comparison of ET and LST Relationships between Energy- and Water-Limited Conditions
Under the water-limited condition, the relationship of ET and LST is always negative across the Ta range from −1 to 15°C. With the assumption of an ET cooling function under the dry and cold condition, therefore, LST-dependent ET models and VI-LST methods can be used for ET estimation. Under the energy-limited condition, however, the ET estimating methods mentioned above do not work and the assumption of an ET cooling function is invalid when Ta ≤ 5°C. The reason for this might be that the energy storage of moist/watered soil and plants is larger than that of dry soil and plants, and it is comparable to available energy for moist/watered soil and plants. This suggests that ET estimation methods based on the land surface energy balance equation might be useful under the energy-limited condition if the energy storage by moist/watered soil and plants is accounted for in the land surface energy balance equation.
4. Conclusions
The energy- and water-limited ET processes should be considered and included in the methods used for ET estimation in cold and dry climates. In this study, the process-based SHAW model along with ground observational data was used to simulate ET and LST in order to understand the relationship of ET and LST under energy- and water-limited conditions. Simulation results indicated that ET and LST have a positive relationship when Ta ≤ 5°C and a negative relationship when Ta > 5°C under the energy-limited condition (SWC = 0.4). However, ET and LST maintain a negative relationship under the water-limited condition (SWC = 0.1). Plant transpiration and energy storage in moist/watered soil and plants can potentially explain the differences in the relationship of ET and LST simulated under the energy-limited and water-limited conditions. Plant transpiration likely affects the relationship of ET and LST due to its relatively strong cooling effect under the energy-limited condition. The energy storage of moist/watered soil and plants, which is comparable to the available energy, has a relatively large contribution to ET when Ta ≤ 5°C. This study suggests that different strategies should be used to estimate ET under the energy-limited condition in a dry and cold climate.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Acknowledgments
This research was supported by the 100 Talents Program of the Chinese Academy of Sciences. This research was also supported by the Grant-in-Aid for Encouragement, Center for Regional Environmental Research, National Institute for Environmental Studies, Japan, and by the Environment Research and Technology Development Fund, the Ministry of Environment, Japan.




