Journal of Fluids
Volume 2016, Issue 1 1453613
Research Article
Open Access

Plane Waves and Fundamental Solutions in Heat Conducting Micropolar Fluid

Rajneesh Kumar, 

Rajneesh Kumar

Department of Mathematics, Kurukshetra University, Kurukshetra 136119, India kuk.ac.in

Search for more papers by this author
Mandeep Kaur, 

Corresponding Author

Mandeep Kaur

Department of Mathematics, Sri Guru Tegh Bahadur Khalsa College, Anandpur Sahib 140124, India sgtbkhalsadu.ac.in

Search for more papers by this author
First published: 13 July 2016
https://doi.org/10.1155/2016/1453613
Academic Editor: Ciprian Iliescu

Abstract

In the present investigation, we study the propagation of plane waves in heat conducting micropolar fluid. The phase velocity, attenuation coefficient, specific loss, and penetration depth are computed numerically and depicted graphically. In addition, the fundamental solutions of the system of differential equations in case of steady oscillations are constructed. Some basic properties of the fundamental solution and special cases are also discussed.

1. Introduction

Eringen [1] developed the theory of microfluids, in which microfluids possess three gyration vector fields in addition to its classical translatory degrees of freedom represented by velocity field. Eringen introduced the micropolar fluids [2] which are subclass of these fluids, in which the local fluid elements possess rigid rotations without stretch. Micropolar fluids can support couple stress, the body couples, and asymmetric stress tensor and possess a rotational field, which is independent of the velocity of fluid. Anisotropic fluids, liquid crystals with rigid molecules, magnetic fluids, cloud with dust, muddy fluids, biologicaltropic fluids, and dirty fluids (dusty air and snow) over airfoil can be modeled more realistically as micropolar fluids. Ariman et al. [3, 4] studied microcontinuum fluid mechanics. Říha [5] discussed the theory of heat conducting micropolar fluid with microtemperature. Eringen and Kafadar [6] developed polar field theories. Brulin [7] discussed linear micropolar media. Flow and heat transfer in a micropolar fluid past with suction and heat sources were discussed by Agarwal and Dhanapal [8]. Payne and Straughan [9] investigated critical Rayleigh numbers for oscillatory and nonlinear convection in an isotropic thermomicropolar fluid. Gorla [10] studied combined forced and free convection in the boundary layer flow of a micropolar fluid on a continuous moving vertical cylinder. Eringen [11] investigated the theory of microstretch and bubbly liquids. Aydemir and Venart [12] investigated the flow of a thermomicropolar fluid with stretch. Yerofeyev and Soldatov [13] discussed a shear surface wave at the interface of an elastic body and a micropolar liquid. The theory of elastic and viscoelastic micropolar liquids was studied by Yeremeyev and Zubov [14]. Hsia and Cheng [15] discussed longitudinal plane waves propagation in elastic micropolar porous media. Hsia et al. [16] studied propagation of transverse waves in elastic micropolar porous semispaces.

Construction of fundamental solution of systems of partial differential equations is necessary to investigate the boundary value problems of the theory of elasticity and thermoelasticity. The fundamental solutions in the classical theory of coupled thermoelasticity were firstly studied by Hetnarski [17, 18]. Hetnarski and Ignaczak [19] studied generalized thermoelasticity. Svanadze [20–25] constructed the fundamental solutions in the microcontinuum field theories. Kumar and Kansal [26] investigated the fundamental solution in the theory of thermomicrostretch elastic diffusive solids. Fundamental solution in the theory of micropolar thermoelastic diffusion with voids was studied by Kumar and Kansal [27]. Recently, Kumar and Kansal [28] discussed plane waves and fundamental solution in the generalized theories of thermoelastic diffusion. Kumar and Kansal [29] studied propagation of plane waves and fundamental solution in the theories of thermoelastic diffusive materials with voids. The information related to fundamental solutions of differential equations is contained in the books of Hörmander [30, 31].

The main objective of the present paper is to study the propagation of plane waves in heat conducting micropolar fluid. Several qualitative characterizations of the wave field, such as phase velocity, attenuation coefficient, specific loss, and penetration depth, are computed and depicted graphically for different values of frequency. The representation of fundamental solution of system of equations in the case of steady oscillations is obtained in terms of elementary functions. Some particular cases have also been deduced.

2. Basic Equations

In three-dimensional space E3, let x = (x1, x2, x3) be the points of the Euclidean space, t represents the time variable, and Dx = (∂/∂x1, ∂/∂x2, ∂/∂x3).

Following Ciarletta [32], the basic equations for homogeneous, isotropic heat conducting micropolar fluids without body forces, body couples, and heat sources are given by
()
where
()
where λ, μ, K, α, β, γ, and c0 are material constants of the fluid. v and Ψ are the velocity vector and microrotation velocity vector, ρ0 is the density, I is a scalar constant with the dimension of moment of inertia of unit mass, K∗ is the thermal conductivity, aT0 is the specific heat at constant strain, T0 is the absolute temperature, T is the temperature change, ϕ∗ is the variation in specific volume, b = (3λ + 2μ + K)αT, where αT is the coefficient of linear thermal expansion, and Δ is the Laplacian operator.
For convenience, the following nondimensional quantities are introduced:
()
where is the characteristic frequency of the medium.
Making use of (2) and (3) in basic equations (1) and after suppressing the primes, we obtain
()
()
()
()
Making use of (7) in (4), we obtain
()
where
()
For two-dimensional problem, we take
()
The relation between dimensionless velocity components v1 and v3 and nondimensional velocity potential functions ϕ and ψ is expressed as
()
Making use of (10)-(11) in (5), (6), and (8), we obtain
()
where .

3. Solution of Plane Waves

For plane harmonic waves, we assume the solution of the form
()
where ω is the circular frequency and ξ is the complex wave number. are undetermined amplitude vectors that are independent of time t and coordinates xm  (m = 1,3). l1 and l3 are the direction cosines of the wave normal onto x1x3-plane with the property .
Using (13) in (12), we obtain
()
The system of (14) will have nontrivial solution, if the determinant of the coefficients vanishes which on expansion yield
()
where
()
Solving (15), we obtain eight roots of ξ, in which four roots of ξ, that is, ξ1,  ξ2,  ξ3, and ξ4, correspond to positive x3-direction and other four roots of ξ, that is, −ξ1,   − ξ2,   − ξ3, and −ξ4, correspond to negative x3-direction. Now and after, we will restrict our work to positive x3-direction. Corresponding to roots ξ1,  ξ2,  ξ3, and ξ4 there exist four waves in descending order of their velocities, that is, two coupled longitudinal waves and two coupled transverse waves.

The expressions for phase velocity, attenuation coefficient, specific loss, and penetration depth of above waves are derived as follows.

(i) Phase Velocity. The phase velocities are given by
()
where V1,  V2,  V3,  V4 are the phase velocities of two coupled longitudinal waves and two coupled transverse waves, respectively.
(ii) Attenuation Coefficient. The attenuation coefficients are defined as
()
where Q1,  Q2,  Q3,  Q4 are the attenuation coefficients of two coupled longitudinal waves and two coupled transverse waves, respectively.
(iii) Specific Loss. The specific loss is the ratio of energy () dissipated in taking a specimen through a rate of stress cycle, to the elastic energy (W) stored in the specimen when the rate of strain is maximum. The specific loss is the most direct method of defining internal friction for a material. For a sinusoidal plane wave of small amplitude, Kolsky [33] shows that the specific loss equals 4π times the absolute value of the imaginary part of ξ to the real part of ξ; that is,
()
where S1,  S2,  S3,  S4 are the specific loss of two coupled longitudinal waves and two coupled transverse waves, respectively.
(iv) Penetration Depth. The penetration depths are defined by
()
where P1,  P2,  P3,  P4 are the penetration depths of two coupled longitudinal waves and two coupled transverse waves, respectively.

4. Steady Oscillations

Let us assume the solution of the form
()
where ω > 0 is the frequency of oscillation.
Making use of (21) into (5), (6), and (8), the system of equations of steady oscillations is obtained as
()
where μ∗ = δ9ιω − 2δ6,  δ∗ = 1 − ιδ4/ω.
The matrix differential operator is taken as
()
where
()
The above system of (22) can be represented in the following form:
()
where V = (v, Ψ, Tf) is a seven component vector function on E3.
Let us assume that
()
F is an elliptic differential operator Hörmander [30], if condition (26) is fulfilled.

Definition 1. The fundamental solution of the system of (21)-(22) (the fundamental matrix of operator F) is the matrix , satisfying condition [30]

()
Here δ is the Dirac delta, is the unit matrix, and x ∈ E3.

Now further G(x) in terms of elementary functions is constructed.

5. Fundamental Solution of System of Equation of Steady Oscillations

We consider the following system of equations:
()
()
()
where H′, H′′ are three-component vector function on E3 and L is scalar function on E3.
The system of (28)–(30) can be written as
()
where Ftr is the transpose of matrix F, Q = (H′, H′′, L), and x ∈ E3.
The following equations are obtained by applying the operator div to (28) and (29):
()
()
()
where .
Equations (32a) and (32c) can be written as
()
()
where
()
()
()
It can be seen that
()
and are the roots of the equation Γ1(−k) = 0 (with respect to k).
From (32b), it is seen that
()
where .
Applying the operators Δ + μ∗ and δ8 curl to (28) and (30), respectively, we obtain
()
()
Now
()
Using (41) and (42) in (40), we obtain
()
Applying the operator Γ1(Δ) to (43) and using (33)-(34), we obtain
()
The above equation can be rewritten as
()
where
()
()
It can be seen that
()
where are the roots of the equation Γ2(−k) = 0 (with respect to k).
Applying the operators δ2 curl and (δ1Δ + δ5ιω) to (29) and (30), respectively, we obtain
()
()
Now
()
Using (47) and (51) in (50), we obtain
()
The above equation may also be written as
()
Applying operator to (53) and using (39), we obtain
()
The above equation can also be written as
()
where
()
From (34), (45), and (55), we obtain
()
where
()
Equations (37), (47), and (56) can be rewritten in the form
()
()
()
where is the unit matrix.
In (59)–(61), we have used the following notations:
()
Now from (59)–(61), we have
()
where
()
The following relation is obtained from (31), (57), and (61):
()
The above relation implies that
()
Let us assume that
()
Let
()
where
()
Now the following lemma will be proved.

Lemma 2. The matrix Y defined above is the fundamental matrix of operator Θ(Δ); that is,

()

Proof. To prove the lemma, it is proved that

()
()
()
We find that
()
Now consider
()
In the similar way, (71b) and (71c) can be proved.

The following matrix is now introduced:

()
From (66), (70), and (74), it is obtained that
()
Hence, G(x) is a solution to (27).

Hence, the following theorem has been proved.

Theorem 3. The matrix G(x) defined by (60) is the fundamental solution of system of (22).

6. Basic Properties of the Matrix G(x)

Property 1. Each column of the matrix G(x) is the solution of the system of (22) at every point x ∈ E3 except the origin.

Property 2. The matrix G(x) can be written as

()

7. Numerical Results and Discussion

The following values of relevant parameters for numerical computations are taken.

Following Singh and Tomar [34], the values of micropolar constants are taken as
()
Thermal parameters are taken as of comparable magnitude:
()
The variations of phase velocities, attenuation coefficients, with respect to frequency have been shown in Figures 1–4 and 5–8, respectively. In Figures 1–8, solid line corresponds to heat conducting micropolar fluid for K = 0.2 (MT1) and dash line corresponds to heat conducting micropolar fluid for K = 0.4 (MT2).
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Variation of phase velocity with frequency ω.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Variation of phase velocity with frequency ω.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Variation of phase velocity with frequency ω.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Variation of phase velocity with frequency ω.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Variation of attenuation coefficient with frequency ω.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Variation of attenuation coefficient with frequency ω.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Variation of attenuation coefficient with frequency ω.
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Variation of attenuation coefficient with frequency ω.

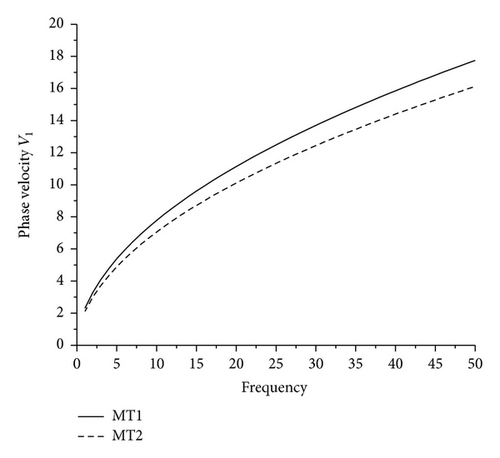
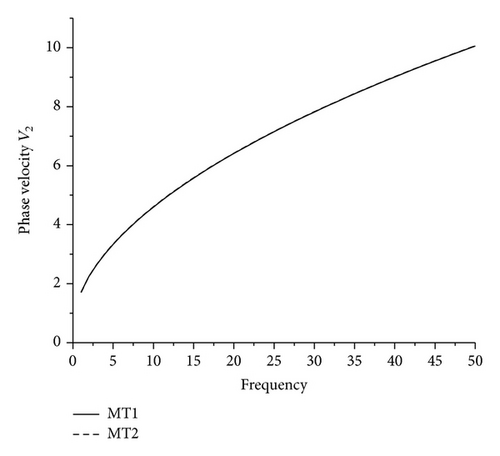
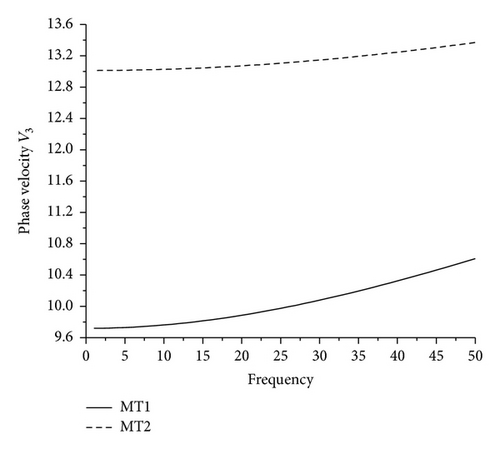
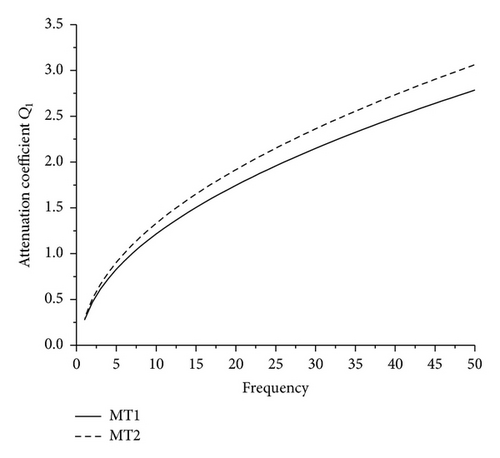
7.1. Phase Velocity

It is noticed from Figures 1–4 that the magnitudes of the phase velocities Vi,   i = 1,2, 3,4, for MT1 and MT2 increase with increase in frequency. The phase velocity V1 for MT1 is greater than the phase velocity for MT2, while for V2,  V3,  V4 the behavior is reversed. This shows that as the value of micropolar constant increases, the phase velocity V1 decreases, while other phase velocities increase. There is slight difference in the phase velocity V2 for MT1 and MT2.

7.2. Attenuation Coefficient

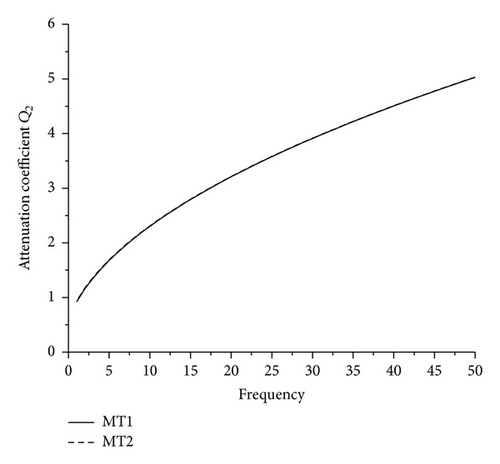
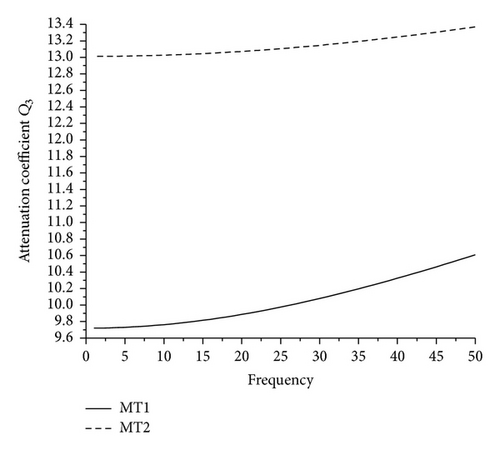
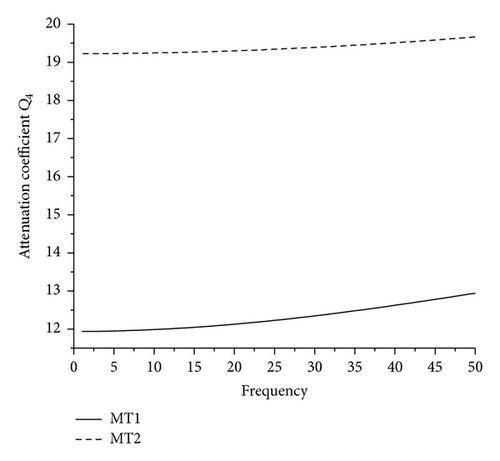
Figures 5–8 depict that the magnitudes of attenuation coefficient Qi,   i = 1,2, 3,4, get increased with increase in wave number ω. It is noticed that, with increase in the value of K, the magnitude of attenuation coefficient increases; that is, the values of attenuation coefficients for MT2 are greater than the values for MT1 that shows the effect of micropolarity.

8. Conclusion

In the present paper, we have studied the propagation of plane waves in heat conducting micropolar fluid. The magnitudes of phase velocities and attenuation coefficients are depicted numerically and presented graphically with respect to frequency. Appreciable micropolarity effect is observed on these amplitudes. It is noticed that the magnitudes of phase velocity Vi,   i = 2,3, 4, and attenuation coefficient Qi,   i = 1,2, 3,4, for K = 0.4 remain more than the magnitude for K = 0.2. This reveals that the more the value of micropolar constant, the more the magnitude of phase velocity and attenuation coefficient. The fundamental solution in heat conducting micropolar fluid in case of steady oscillations in terms of elementary functions is also constructed in the present study.

Competing Interests

The authors declare that they have no competing interests.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.