Autopilot Design Method for the Blended Missile Based on Model Predictive Control

1. Introduction

The emergence of highly maneuverable targets has brought new challenges to guidance technology. The improvement of homing guidance performance against highly maneuverable targets in the future guided missiles requires the control system to have faster response and wider operation range [1]. In the meantime, as an important property of advanced missiles, multiple actuators are often employed to enhance maneuverability as well as interception probability. For example, both aerodynamic surfaces and reaction jets are employed in the control system of PAC-3.

With a higher angle of attack, the missile dynamic model is highly nonlinear and the coupling effects [2] as well as the uncertainties in both aerodynamic parameters and reaction jet thrust are oblivious. Munson and Garbrick introduced amplification factors to describe the lateral jet interference effect [3]. Graham and Weinacht studied the interaction between the side jet and the external flow by a numerical method [4]. It is obvious that the autopilot designed using the linearized model around an operation point is usually unable to achieve satisfactory performance over a full flight envelope. Recently, many nonlinear control methods are proposed for the design of conventional aerofin autopilots. For instance, the gain-scheduled approach was proposed in [5], where linear parameter varying transformations were adopted.

On the other hand, the autopilot design for blended missile has not been much reported, which is more complicated than that of conventional aerofin autopilot due to the heterogeneous actuation [1]. Hirokawa et al. [1] designed an autopilot for the case with aerodynamic surfaces and reaction jet using the coefficient diagram method (CDM). The feasibility of the autopilot based on variable structure was discussed in [6], where a simple blending strategy is investigated: aerodynamic control is used at low angles of attack while reaction jet control is used when the missile moves beyond the stall region. Optimal control and static control allocation were combined in [7] to address the issue of dual control missile while a dynamic control allocation method was presented in [8].

In addition, for the autopilot design of blended missiles (such as PAC-3), two aspects of control input constraints should be taken into account: the saturation constraint on aerodynamic surfaces and the finite set constraint on reaction jets. However, they are not simultaneously considered in the aforementioned work. Besides, the hybrid properties of control inputs (continuous aerodynamic surfaces and on-off reaction jets) are often neglected as in [6–8]. Motivated by these facts, this paper attempts to design an autopilot using explicit hybrid MPC for blended missiles, by noting that MPC is a promising methodology for the control problem of constrained uncertain systems [9] and that the computational burden of on-line optimization is effectively reduced by using explicit MPC instead of traditional MPC [10].

The remainder of this paper is as follows. Section 2 gives a mathematical model of blended missile including the configuration of reaction jets. In Section 3, the piecewise affine model of blended missile is established, followed by an MLD model which is obtained based on the equivalence of piecewise affine model and mixed logical dynamical model. In Section 4, a hybrid MPC based method for autopilot design is proposed and an explicit control law is constructed. In Section 5, the effectiveness of the proposed method is verified by simulation cases under different conditions. Finally, several concluding remarks are given in Section 6.

2. Mathematical Model of the Missile

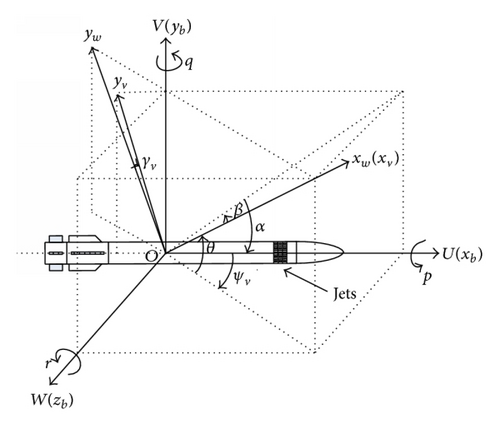
The plane reference coordinate system OUVW, the body coordinate system Ox_by_bz_b, the trajectory coordinate system Ox_wy_wz_w, and velocity coordinate system Ox_vy_vz_v are involved in this paper. Figure 1 shows a missile with some key variables and identified axes. The axes z_w, z_v are not given, whose directions can be determined by the right hand rule.

2.2. Lateral Jet Forces and Moments Model

As shown in Figure 1, the lateral jet force is generated by 180 pulse jets located in front of the center of mass of PAC-3. These jets are divided into 10 rings and arranged in staggered positions (18 pulse jets are included in each ring). In each ring, these jets are uniformly distributed and the central angle between two neighboring jets is 20 degree. Use i (i = 1,2, …, 10) and j (j = 1,2, …, 18) to denote the ring’s label and the jet’s label in each ring, respectively. The distance between ring i and the center of mass is denoted by l_i, while spacing of adjacent rings is Δl. The layout scheme of pulse jets is shown in Figures 2 and 3. Assume the force generated by each individual jet is a constant F_m. In body coordinate system, the lateral force generated by the (i, j) pulse jet is given by

$$ (4)

The corresponding moment is given by

$$ (5)

where

$$ (6)

For the situation where all pulse jets are fired at the same time, the total force and moment are given by

$$ (7)

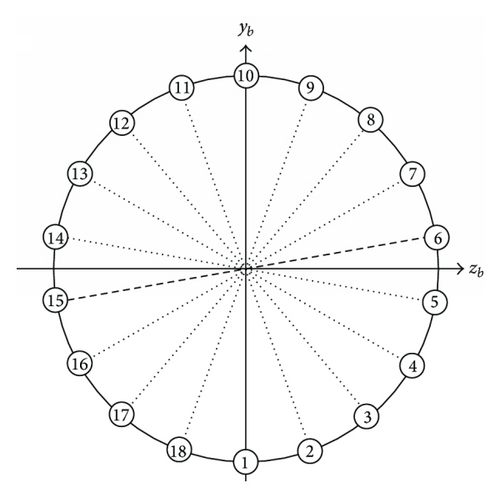
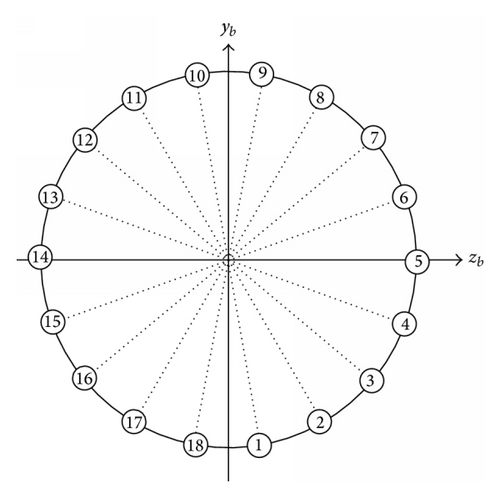
In order to avoid the coupling between the pitch moment and yaw moment, each ring is divided into four control regions: positive pitch, negative pitch, positive yaw, and negative yaw control region, as shown in Figure 4.

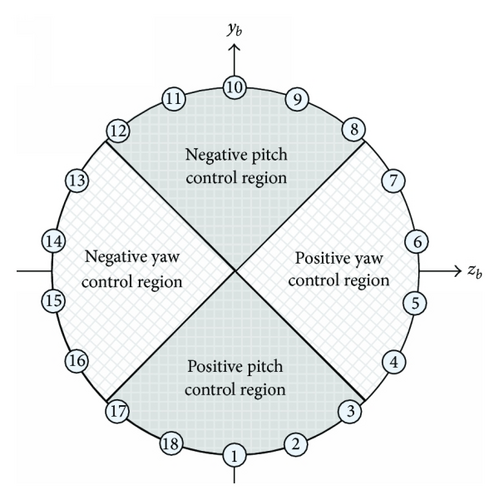
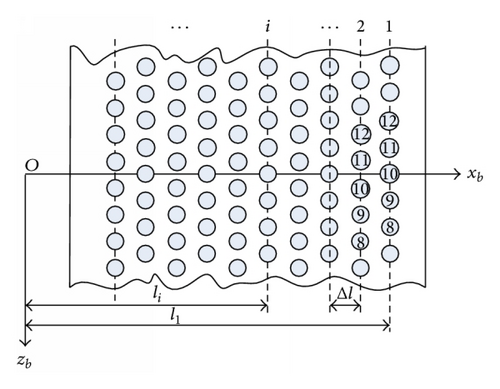
The autopilot design of PAC-3 is more complicated than that of other conventional missiles which are controlled only by aerodynamic surfaces, due to the hybrid property of control inputs and the on-off property of pulse jet (the pulse jet can be fired only one time). To deal with this problem, the work [7] proposed two-step design procedures: (1) in the first step, neglect the hybrid property (or on-off property) and design the expected force and moment signals, (2) in the other step, the fire logic is derived by solving the retaliation problem of these signals, with taking into account the hybrid property (or on-off property). Different from the above traditional procedures, a novel procedure will be presented in what follows, where only one step is included. In practical applications, only a small number of jets (in a certain of rings) are activated over a finite time interval. To make the idea of the following development clear, we here consider a simple but representative situation, where no more than two rings are allowed to be fired simultaneously and no more than two jets are activated in each fired ring. Meanwhile, it should be ensured that only odd rings or even rings are fired, and the jets are fired symmetrically about the corresponding symmetry axis of each control region.

Take the positive pitch control region as an example. The forces provided by the jets (i, 1), (i, 2), (i, 3), (i, 17), and (i, 18) in an odd ring are given by

$$ (8)

Similarly, the forces provided by the jets (i, 1), (i, 2), (i, 17), and (i, 18) in an even ring are given by

$$ (9)

where F_o and F_e denote the forces associated with an odd ring and an even ring, respectively.

Use Fⁱ to denote the lateral force generated by ring i. Clearly, Fⁱ should satisfy the condition

$$ (10)

When odd ring is fired, the lateral force and moment are given by

$$ (11)

While even ring is fired, the lateral force and moment are given by

$$ (12)

Noting Δl is quite small, we consider l₅≃l₆ = l. In order to ensure that the jets fire efficiency, the jets resulting in small moment components along z_b axis are not activated. As a result, the sets of forces and moments are, respectively, given by

$$ (13)

$$ (14)

where $$ and $$. During each control period, a control moment belonging to $$ will be used as the input.

The mutual interference between high-speed jet stream and air leads to lateral jet interference effect. In order to take into account this interference, force and moment amplification factors $$, $$, $$, and $$ are introduced as in [3, 4]. Then, the resulting lateral forces and moments are

$$ (15)

Remark 1. In fact, each pulse jet can be fired only once, so the location of the fired jet cannot provide force anymore. Based on this precondition, elements of sets $$ and $$ will be less and less over time. In this paper, quantity change of sets’ elements is not considered to simplify the problem.

3. Mixed Logical Dynamical Model of Blended Missile

3.1. Piecewise Affine Model of Blended Missile

To simplify analysis, the gravity term and the channel coupling term are ignored. With (16), the missile attitude control model of pitch channel is

$$ (17)

Choose x = [α r] ^T as system state and $$ as control input. The considered output is y = α. Then, (17) can be rewritten into the following state space form:

$$ (18)

where

$$ (19)

The missile parameters are presented in Table 1.

Table 1. Missile’s overall parameters.

Missile’s takeoff mass [kg]	255
Missile’s full-length [m]	4.86
Missile’s diameter [m]	0.317
Distance between missile head and center of mass [m]	2.569
Moment of inertia Jx, Jy, Jz [kg⋅m2]	3.03, 306.3, 306.3
Lateral force provided by individual jets [N]	2200
Distance between jet ring center and center of mass [m]	1.26
Range of angle of attack [rad]	$$
Range of pitch angular velocity [rad/s]	$$
Range of elevator deflection [rad]	$$

Generally, the aerodynamic coefficients $$, $$, $$, and $$ and the amplification factors $$, $$ are mainly affected by the flight velocity V and the angle of attack α [11, 12]. Since the terminal guidance phase is considered in this paper, the flight time is quite short and the flight velocity of the missile can be treated as a constant. Thus, the aerodynamic coefficients and the amplification factors are mainly affected by the angle of attack α. The relationships between them are shown in Figure 5.

In practical application, since α is the main factor that leads to system nonlinearities, the system model is usually linearized if α varies in small range. As seen from Figure 5, curves of the relation between aerodynamic parameters and angle of attack can be expressed by six line segments approximately. Here, we choose α = −0.37 rad, −0.153 rad, 0,0.153 rad, and 0.37 rad as the operation points and divide the whole operation region into six subregions. As a result, the original model (17) can be converted to the following piecewise affine models:

$$ (20)

$$ (21)

where

$$ (22)

where i (i = 1,2, …, 6) is the label corresponding to the ith region.

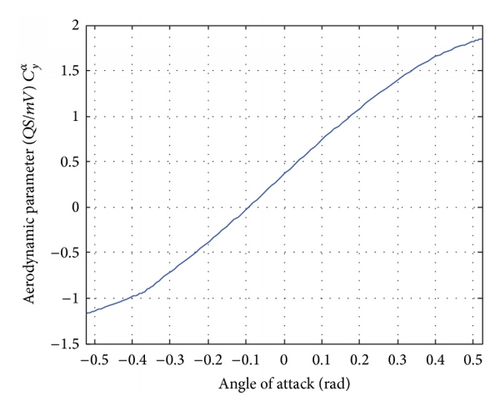
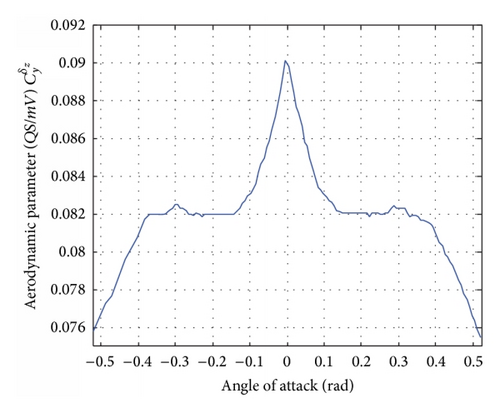
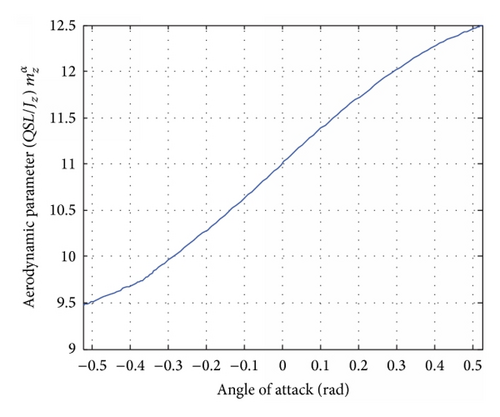
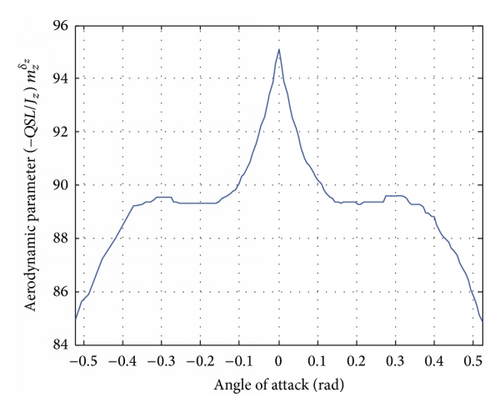
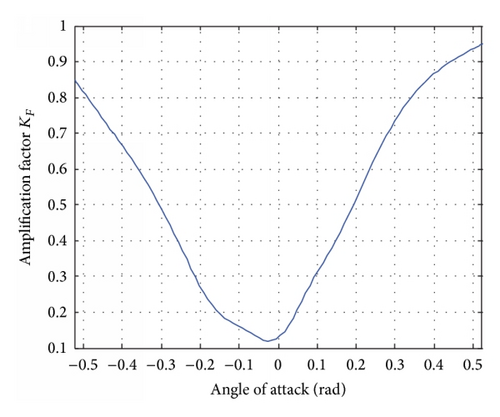
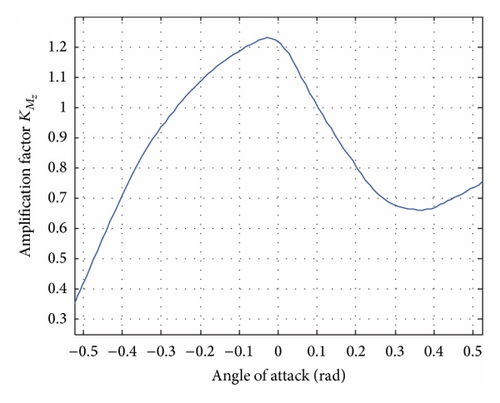
From Table 1 and Figure 5, we get the set of aerodynamic parameters at the point (H, V) = (20 km, 1000 m/s) as shown in Table 2.

Table 2. Aerodynamic parameters of pitch channel.

Aerodynamic parameter	$$	$$	$$	$$	$$
α = −0.53	− 1.175	0.076	9.47	− 0.32	− 84.89
α = −0.37	− 0.944	0.082	9.73	− 0.32	− 89.24
α = −0.153	− 0.23	0.082	10.43	− 0.32	− 89.38
α = 0	0.36	0.09	11.01	− 0.32	− 95.10
α = 0.153	0.94	0.082	11.58	− 0.32	− 89.34
α = 0.37	1.63	0.082	12.24	− 0.32	−89.18

Choose the sampling period T_s = 0.025 s. The discrete state-space expression is then given by

$$ (23)

$$ (24)

where

$$ (25)

4. Autopilot Design Using Hybrid MPC Method

Different control allocation between the dual actuators (aerodynamic control surfaces and lateral pulse jets) can be obtained by setting different Q and R. Since both logical and continuous variables are involved in (41), the above on-line optimization problem is a mixed integer quadratic programming (MIQP) problem which can be solved by using the hybrid MPC toolbox of MATLAB [14, 15].

5. Numerical Simulations

5.1. Case 1

Numerical simulations are performed to verify the feasibility of the proposed method in this section. The involved parameters are given in Table 1. The weight matrices are set as Q = 10, $$, and $$. Suppose the initial state is α₀ = 0, r₀ = 0. In order to avoid excessive computational load, we choose predictive horizon N = 2 and control horizon M = 2. The command for angle of attack is α_c = 0.2 rad.

Explicit form of the optimal controller is provided by hybrid toolbox, which is not given here for simplicity. Instead, we present the partition results associated with the controller in Figure 6, where 4190 subregions are obtained and, for each subregion, a control law of the form u = Kx + b is given. As a benefit of using explicit MPC, the controller parameters K and b for all the subregions are obtained simultaneously once the optimization problem is solved. This property is obviously different from that of gain-scheduled controller (where the controller parameters for different regions are separately determined).

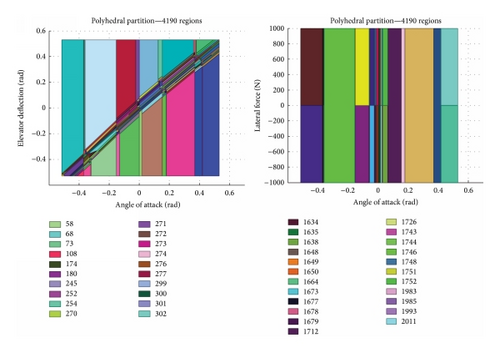
However, by a simple calculation, we conclude that these subregions do not require too much storage space (the needed storage space is approximately 14 × 8 × 4190 = 450 KB). Moreover, it should be noted that when the algorithm is implemented in practice, much more time will be needed to identify which subregion the current states enter into. This is another important factor that affects the computational cost of the proposed algorithm.

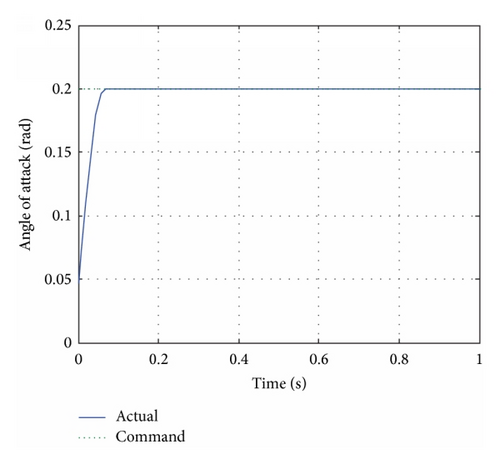
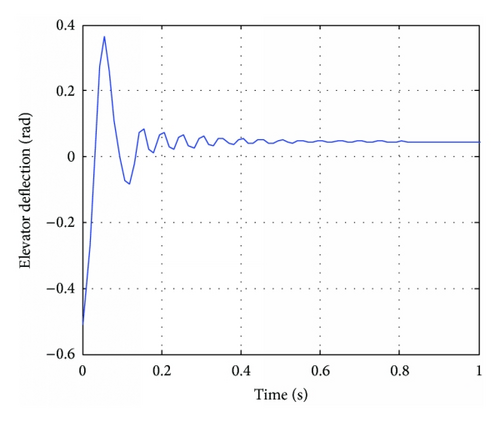
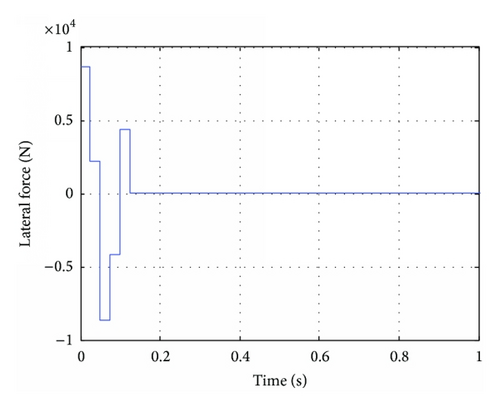
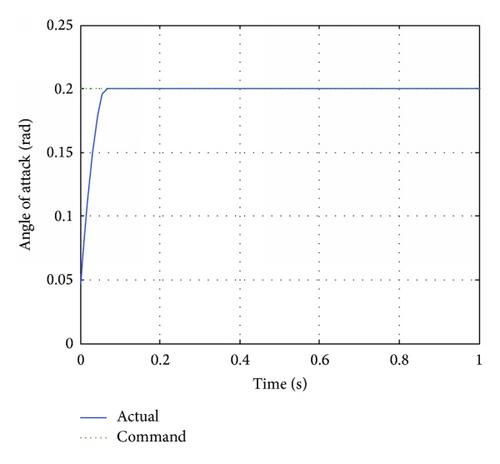
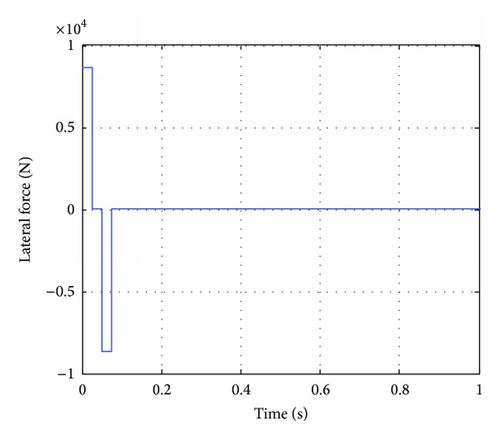
The simulation results are shown in Figures 7–9. It is seen from Figure 7 that the actual angle of attack tracks the command in less than 0.1 seconds. As shown in Figures 8 and 9, the aerodynamic force converges to a constant as time increases while the jets are only activated during the beginning period (when the tracking error is obvious).

5.2. Case 2

The results for the case with a different weight $$ are shown in Figures 10–12. It is seen that a different control allocation result is obtained.

5.3. Case 3

In this case, a different command α_c = 0.2cos⁡(0.5πt) rad is considered and the weight matrices are the same as the ones for Case 1. The simulation results are shown in Figures 13–15.

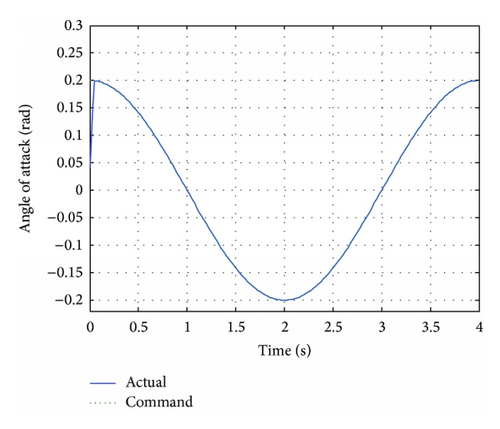
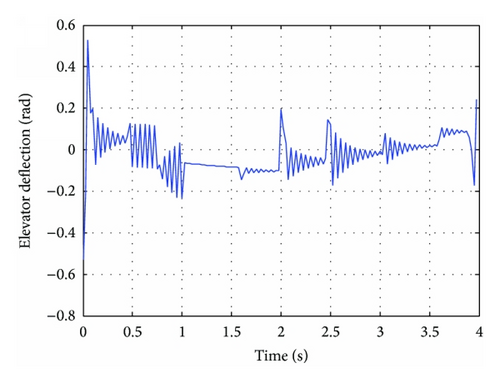
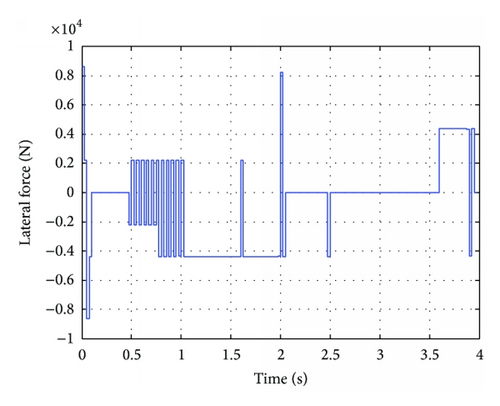
It is seen from Figure 13 that asymptotic tracking is also achieved. The method proposed in this paper can realize both fast tracking command and control allocation. It is seen from Figure 15 that the jets are activated, while the tracking error is obvious or command is varying rapidly.

6. Conclusion

An autopilot design method for a missile with aerodynamic control surfaces and lateral jets is presented in this paper. The nonlinear attitude control model is reduced to an MLD model. Meanwhile, the lateral force is described as linear combination of logical variables due to the discrete values of lateral force. Then the whole MLD model of attitude control system is derived. Autopilot design is accomplished using hybrid MPC method. By setting the related weighted coefficients in index function, the control allocation is obtained. Moreover, numerical simulations are performed under the different conditions, the performance of tracking the attitude command and control allocation is verified, and the explicit form of the control law can be obtained as well.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.