International Journal of Aerospace Engineering

Volume 2015, Issue 1 538901

Research Article

Open Access

Projection-Based Adaptive Backstepping Control of a Transport Aircraft for Heavyweight Airdrop

Ri Liu,

Ri Liu

Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China afeu.cn

Search for more papers by this author

Xiuxia Sun,

Xiuxia Sun

Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China afeu.cn

Search for more papers by this author

Wenhan Dong,

Corresponding Author

Wenhan Dong

[email protected]

Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China afeu.cn

Search for more papers by this author

Guangzhi Xu,

Guangzhi Xu

Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China afeu.cn

Search for more papers by this author

Ri Liu,

Ri Liu

Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China afeu.cn

Search for more papers by this author

Xiuxia Sun,

Xiuxia Sun

Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China afeu.cn

Search for more papers by this author

Wenhan Dong,

Corresponding Author

Wenhan Dong

[email protected]

Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China afeu.cn

Search for more papers by this author

Guangzhi Xu,

Guangzhi Xu

Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China afeu.cn

Search for more papers by this author

First published: 31 December 2015

https://doi.org/10.1155/2015/538901

Citations: 2

Academic Editor: Christopher J. Damaren

Share a link

Email
Wechat
Bluesky

Abstract

An autopilot inner loop that combines backstepping control with adaptive function approximation is developed for airdrop operations. The complex nonlinear uncertainty of the aircraft-cargo model is factorized into a known matrix and an uncertainty function, and a projection-based adaptive approach is proposed to estimate this function. Using projection in the adaptation law bounds the estimated function and guarantees the robustness of the controller against time-varying external disturbances and uncertainties. The convergence properties and robustness of the control method are proved via Lyapunov theory. Simulations are conducted under the condition that one transport aircraft performs a maximum load airdrop task at a height of 82 ft, using single row single platform mode. The results show good performance and robust operation of the controller, and the airdrop mission performance indexes are satisfied, even in the presence of ±15% uncertainty in the aerodynamic coefficients, ±0.01 rad/s pitch rate disturbance, and 20% actuators faults.

1. Introduction

Heavyweight airdrop is an essential capability of a large transport aircraft, and it is critical to the success of many military tasks, such as precision delivery of heavyweight equipment and supplies [1, 2]. To perform these tasks with accurate allocation of the payload and to also guarantee flight safety, highly stable aircraft dynamics are required. However, the continuous movement and sudden delivery of the heavy cargo can exert large disturbances on the aircraft, thus leading to considerable deviation of the aircraft dynamics from the trim position [3–5]. Therefore, the design of an aircraft controller that is compatible with heavyweight airdrop tasks is necessary, and the large and sudden disturbances, strong coupling between the cargo and aircraft dynamics, and multiple uncertainties make this a challenging task [6–11].

Over recent years, various meaningful achievements have been reported in developing advanced aircraft controllers that are compatible with airdrop tasks. Several control methods that use a linearized model at a given operating point have been proposed in the literature, including L1 adaptive control [6], robust control [7], and active disturbance rejection control [12, 13]. Although these approaches can improve various aspects of system performance, one shortcoming is that satisfactory performance and robustness are difficult to achieve in the event that the cargo becomes increasingly heavy. In such an event, the aircraft dynamics can change rapidly and deviate far from the operating point, which yields a highly nonlinear system. Many nonlinear control approaches have been developed to handle systems with strong nonlinearities. The theoretically established feedback linearization method is the one that is most widely applied [14–18].

The nonlinear system can be decoupled via exact state transformations rather than linear approximations. However, to perform perfect linearization, accurate knowledge of the plant dynamics must be available. This is not the case for airdrop flight controller design, as the complex nonlinear aerodynamic characteristics are very difficult to ascertain and model precisely [4, 6, 7, 10]. Moreover, aerodynamic data obtained from wind tunnel tests, augmented by computational fluid dynamics results, always contain a certain degree of uncertainty. The problem of model deficiencies can be dealt with by closing the control loop with robust controllers, for instance, combining feedback linearization with sliding mode control [8–10] or backstepping sliding mode control [11]. These methods devise control laws based on the knowledge of the bounds on the relevant uncertainties. However, the bounds of the complex nonlinear uncertainties, which are composed of aircraft-cargo dynamics coupled with aerodynamic perturbations, are difficult to obtain in advance. Thus, the control gains need to be set large enough to operate correctly under a variety of conditions, which is generally a very conservative strategy. This approach might also lead to severe chattering phenomena and could damage actuators and systems [19–21].

In these cases, nonlinear adaptive control methods are called for. Adaptive backstepping control [22–26], which allows uncertainties of both matched and mismatched type, has been widely applied to flight control projects [23–26]. To be able to estimate the nonlinear uncertainties of the system, it is possible to employ neural networks within the parameter update laws of the adaptive backstepping controller [22, 23]. The neural networks are used to parameterize the nonlinear uncertainties, and this allows the update laws to adapt to the network weights. In spite of their obvious conceptual appeal, the complicated computations are time-consuming and the stability analysis is tedious. These considerations might limit the application of this method in the design of airdrop flight controllers from a purely practical perspective. One interesting technique is to separate the uncertain parameters from the complex nonlinearities and use update laws to adapt the uncertain parameters directly [26]. The design procedure, as well as the performance analysis of such an approach, is relatively easy when compared with that using the neural networks method.

The main motivation for the current work is to propose a simplified controller design for the airdrop mode that can accommodate large changes in aircraft dynamics and reject uncertainties of both constant and time-varying types, as well as matched and unmatched types. The contributions of this paper are (1) a flight controller design that inherits the merits of the backstepping approach, thus solving the unmatched control problem of cargo airdrop; (2) the introduction of adaptation theories to estimate the system uncertainties, which overcomes the conservative drawbacks of [8–11] as discussed above; (3) the formation of adaptation laws using the projection operator to bound the estimated functions and theoretically guarantee the robustness of the controller against time-varying disturbances and uncertainties while avoiding singularity of the control law; and (4) a proof of the convergence properties and robustness of the control method based on Lyapunov theory.

The structure of this paper is as follows. The aircraft-cargo model with cargo extraction is presented in Section 2. The control law for the airdrop mode is derived in Section 3, along with a discussion of the stability properties. Section 4 presents simulation results that verify the correct operation of the proposed controller, and conclusions are presented in Section 5.

2. Aircraft-Cargo Model with Cargo Extraction

As stated in the previous section, this paper studies the design of a flight control law for the airdrop operations. The governing equations of motions are recalled from [10] as

(1)

(2)

(3)

(4)

where m_b is the mass of the aircraft; V is the airspeed; α is the angle of attack (AOA); γ is the climb angle and θ = γ + α with θ being the pitch angle; q is the pitch rate; I_y is the pitch moment of inertia; T, D, L, and M_y are the engine thrust, drag, lift, and pitch aerodynamic moment, respectively; and F_cx, F_cz, and M_c are the disturbance forces and moment, respectively, that the cargo imposes on the aircraft.

The pitch aerodynamic moment is obtained as

(5)

where

is the dynamic pressure; S is the wing area; δ_e is the elevator deflection; c_A is the mean aerodynamic chord; and

are the pitch moment coefficients. The drag and lift are found by

(6)

where

and

are the drag and lift coefficients, respectively. The engine thrust is

(7)

where δ_p is the throttle opening ranging from 0 to 100% and T_m is the maximal thrust.

F_cx, F_cz, and M_c are obtained as

(8)

where m_c is the mass of the cargo; F_p is the extraction force where F_p = m_cgλ with λ denoting the extraction ratio; and r_c is the position of the cargo with respect to the center of gravity (CG) of the aircraft. The cargo dynamics are found by

(9)

where μ is the friction coefficient of rolling between the cargo and the roller on the floor.

Remark 1. It is observed from (1)–(3) and (8) and (9) that the aircraft-cargo dynamics form a strongly nonlinear system subject to the coupling of the aircraft states and the cargo parameters. The system may be further complicated by various uncertainties, such as aerodynamic data perturbation and uncertain machinery faults. Readers can refer to [10] for detailed discussions about the model.

From (1)–(9), together with the consideration of uncertainties, the aircraft-cargo model can be rewritten in the following form:

(10)

where x₁ = θ, x₂ = [V, q]^T,

, B = [0,1],

, and

;

is the uncertainty function; σ(t) ∈ R is the unknown time-varying disturbance; and ω ∈ R^2×2 is the unknown input gain matrix. f_i and g_ij (i = 1,2; j = 1,2) are found by

(11)

with Λ_i (i = 1,2, 3) being defined as follows:

(12)

The uncertainty function Δf_i (i = 1,2) introduced by the aerodynamic data perturbation is obtained as

(13)

Here,

, and

are the perturbation of the lift, drag, and pitch moment coefficients, respectively. We introduce the following notations:

(14)

Then, ΔF(t) can be written as

(15)

We will use the following assumptions throughout this analysis.

Assumption 2 (uniform boundedness of σ(t) and P(t)). Here, |σ(t)| ≤ ϕ and P(t) ∈ Θ, where ϕ > 0 is a known bound of σ(t) and Θ is a known compact set.

Assumption 3 (partial knowledge of the input gain matrix). ω is a constant diagonal matrix defined as ω = diag⁡(ω₁₁, ω₂₂) with 0 < ω₁₁, ω₂₂ ≤ 1. There exists a known compact set Ω such that ω ∈ Ω ⊂ R^2×2.

Assumption 4 (uniform boundedness of the rate of variation of parameters). σ(t) and P(t) are continuously differentiable with uniformly bounded derivatives; that is, and with ‖(·)‖ denoting the 2-norm of the vector.

3. Control Law and Stability Properties

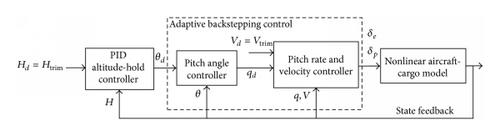
The overall control system is designed using three feedback loops, as shown in Figure 1. The third loop (outer loop) uses an altitude-hold controller designed using the regular PID control law. This loop generates a pitch angle command input θ_d for the angular control loop in the second layer. The inner loop contains two controlled variables that are [q, V] ^T. The pitch rate command q_d is generated by the angular control loop, and the velocity command V_d is the trim value.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Autopilot control architecture with three layers of feedback.

3.1. Adaptive Backstepping Control Law

The steps in the adaptive backstepping control law are described below.

Step 1. Consider the first equation in system (10):

(16)

The desired pitch angle is x_1d(t) = θ_d, and design the virtual control law of (16) as

(17)

where k₁ > 0 and

is the estimation of σ(t), which is governed by

(18)

where Γ > 0 is the adaptation gain and Proj⁡(·, ·) is the projection operator (see the appendix for details) which ensures that

Step 2. Consider the second equation in system (10):

(19)

The control law is designed as

(20)

where k₂ > 0 is a constant matrix represented by k₂ = diag⁡(k₂₁, k₂₂, k₂₃).

and

are governed by

(21)

where the projections are confined to the sets Ω and Θ, respectively; that is,

and

Remark 5. The projection-based adaptation law ensures that is nonsingular. For instance, we can set

(22)

From

, it follows that

is always nonsingular. For −2/π < α < 2/π, we have |g₁₁g₂₂| ≪ |g₁₂g₂₁| [8, 10], which, together with the condition that

is nonsingular, implies that

is nonsingular.

3.2. Stability Analysis

The proof of stability of the control law is achieved by augmenting Lyapunov functions for the state tracking errors and parameter estimation errors. We define

(23)

Taking the time derivative of

yields

(24)

and the time derivative of

(25)

Theorem 6. Given the system in (10) controlled by (20) with the adaptation laws defined via (18) and (21), the state tracking errors , i = 1,2, are uniformly bounded:

(26)

where l = (1/k_min⁡)(d_σϕ + max_P∈Θ⁡‖P‖d_P) + 2(ϕ² + max_ω∈Ω⁡tr⁡(ω^Tω) + max_P∈Θ⁡‖P‖²),

, and

Proof. Consider the Lyapunov function candidate:

(27)

First, we prove that υ(t) ≤ l/Γ. Since the aircraft should maintain a straight and level flight condition before the cargo is unlocked [6–11], we have

. Then, we can verify that

(28)

The time derivative of υ(t) along the solutions of (24) and (25) is

(29)

Substituting (18) and (21) into (29) leads to

(30)

Using Property A.2 of the projection operator (see the appendix for details), we can obtain that

(31)

which implies that

(32)

From

, and Assumption 4, we have

(33)

(34)

If there exists t^′ > 0 such that υ(t^′) > l/Γ, it then follows from (27) and (34) that

(35)

which further leads to

(36)

Thus, if υ(t^′) > l/Γ, then from (32), (33), and (36), we obtain

(37)

Since υ(0) ≤ l/Γ, υ(t) ≤ l/Γ holds for every t ≥ 0. Notice that if

, then

. This proves the bounds in (26).

Remark 7. Such a projection-based adaptation law can bound the estimated function, and this theoretically guarantees the robustness of the controller against time-varying disturbances and uncertainties. However, the stability properties of systems using conventional adaptation laws are provable only under the assumption of constant disturbances and uncertainties [23, 26].

Remark 8. It follows from (26) that one can prescribe the arbitrary desired tracking performance by increasing the adaptation gain Γ. However, a large gain requires more control power and can also lead to control signal oscillations. Thus, the adaptation gain needs to be tuned in a trial-and-error way.

4. Simulation Analysis

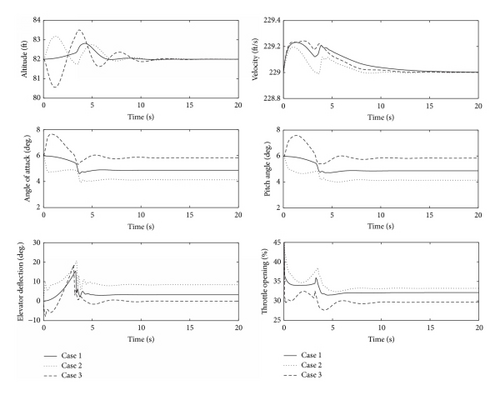
To verify the proposed controller design, a 24,955 kg transport aircraft performing an airdrop of cargo weighing 8,000 kg is simulated. The cargo is initially locked at the CG of the aircraft. The aircraft is trimmed at the following conditions: H₀ = 82 ft, V₀ = 229 ft/s, and α₀ = θ₀ = 5.9813 deg. with δ_p = 34.1%, δ_e = 0 deg., the horizontal stabilizer δ_h = −5.4093 deg., and the flap δ_f = 25 deg.

To satisfy the requirements of mission completeness and flight safety, the performance indexes for the heavyweight airdrop are given as follows [8]: (1) |ΔH| ≤ 45 ft and H_min > 20 ft; (2) |ΔV| ≤ 0.13V₀; (3) |Δθ| ≤ 5 deg. and θ > 2 deg.; and (4) α_max ≤ 0.7α_s with α_s denoting the stalling AOA.

The performance and robustness of the controller are first tested in the presence of constant disturbances, actuators faults, and uncertainties. The following three cases are simulated and compared.

Case 1. In the first case, σ = 0, , and ω = diag⁡(1,1).

Case 2. In the second case, σ(t) = 0.01 rad/s, , and ω = diag⁡(0.8,0.8).

Case 3. In the third case, σ(t) = −0.01 rad/s, , and ω = diag⁡(0.8,0.8).

The compact sets can be conservatively set to ϕ = 0.3, Θ = {b = (b_i) _7×1 ∈ R^7×1 : b_i ∈ [−2,2]}, and Ω is set as in Remark 5 (in Section 3.1). After experimental tuning, we select k₁ = 8, k₂ = diag⁡(3,5, 1), and Γ = 20. The outer-loop altitude-hold PID controller parameters are set as K_p = 0.05, K_I = 0.033, and K_D = 0.009. Figure 2 shows simulation results of the drop process for these three cases, and we can see that the criteria for a successful drop have all been met. In all three cases, the altitude increment is controlled in the range of 2 ft. After the cargo is dropped out, the altitude and the velocity are well maintained at the predefined trim position and fully stabilized within 12 seconds. Owing to the loss of heavy weight, the final AOA and pitch angle become smaller when compared to that of the trim position, especially in Case 2. The observed change in value is less than 5 deg., and the final pitch angle is greater than 2 deg., which meets the mission performance indexes. The elevator deflection and the throttle opening are within the magnitude limits, and there is no severe chattering problem. To summarize, the pitch-up motion of the aircraft by the release of the cargo is suppressed effectively through appropriately configuring the elevator and the throttle, even in the presence of ±15% aerodynamic coefficients uncertainty, ±0.01 rad/s pitch rate disturbance, and 20% actuators faults.

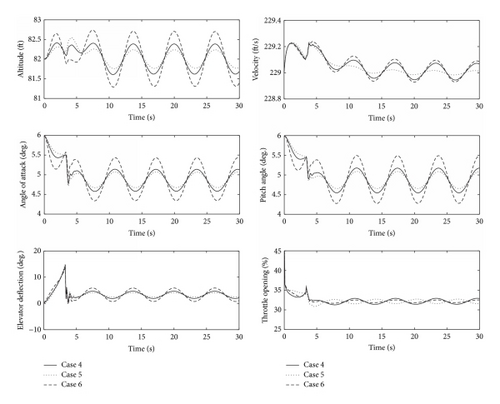
Next, we test the performance and robustness of the control system for the condition of time-varying disturbances and uncertainties, without retuning the parameters of the controller. Note that no actuators faults are considered in the following test (i.e., ω = diag⁡(1,1)). The external disturbances and uncertainty function are set as follows.

Case 4. In this case, σ(t) = 0.01sin⁡(t) rad/s, .

Case 5. In this case, σ = 0, .

Case 6. In this case, σ(t) = 0.01sin⁡(t) rad/s, .

Figure 3 shows that the flight altitude is controlled in the range of [81 ft, 83 ft], the velocity increment is less than 0.3 ft/s, and the pitch angle as well as the AOA converges to within [4 deg., 5.5 deg.]. The responses of the aircraft can meet the mission performance indexes for Cases 4–6, which verifies the robustness of the control method against time-varying disturbances and uncertainties.

5. Conclusions

This paper focused on the problem of designing an aircraft controller compatible with heavyweight airdrop operations. To achieve good stability and robust characteristics, a novel flight controller combining backstepping control with adaptive function approximation was developed for pitch attitude and velocity control. This method uses projection-based adaptation strategies to achieve robustness against uncertainties. Lyapunov-based analysis shows that the controller ensures uniformly bounded steady-state tracking errors in the presence of constant actuators faults, time-varying external disturbances, and aerodynamic uncertainties. The performance of the controller was evaluated in a maximum load airdrop mission. Simulation results verified that the controller performance satisfies the airdrop mission performance indexes in the presence of pitch rate disturbances, aerodynamic uncertainties, and actuators faults. The application of this research can be used to achieve higher levels of performance and safety in practical airdrop missions.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (Grant no. 60904038) and the Aviation Science Foundation of China (Grant no. 20141396012).

Appendix

Projection Operator

The projection operator introduced in [27] bounds the estimated parameters by definition. We recall the main definitions from [27].

Definition A.1. Consider a convex compact set with a smooth boundary given by

(A.1)

where f : Rⁿ → R is the following smooth convex function:

(A.2)

where θ_max is the norm bound imposed on the vector θ and 0 < ε_θ < 1 stands for the projection tolerance bound of our choice. For any given y ∈ Rⁿ, the projection operator is defined as

(A.3)

where ∇f(θ) is the gradient vector of f(·) evaluated at θ and

(A.4)

The properties of the projection operator are given by the following lemma.

Lemma A.2. Let

(A.5)

and let the parameter θ(t) evolve according to the following dynamics:

(A.6)

Then

(A.7)

for all t ≥ t₀, and

(A.8)

Property A.1. The projection operator Proj⁡(θ, y) does not alter y if θ belongs to the set Ω₀. In the set {0 ≤ f(θ) ≤ 1}, Proj⁡(θ, y) subtracts a vector normal to the boundary of Ω_c to obtain a smooth transformation from the original vector field y to an inward or tangent vector field for c = 1. Therefore, on the boundary of Ω_c, always points toward the inside of Ω_c and θ(t) never leaves the set Ω_c.

Property A.2. From the convexity of function f(θ), it follows that, for any θ^∗ ∈ Ω₀ and θ ∈ Ω_c, the inequality

(A.9)

holds. It then follows from Definition A.1 that

(A.10)

References

1 Desabrais K. J., Riley J., Sadeck J., and Lee C., Low-cost high-altitude low-opening cargo airdrop systems, Journal of Aircraft. (2012) 49, no. 1, 349–354, https://doi.org/10.2514/1.c031527.
10.2514/1.C031527
Web of Science® Google Scholar
2 Pang S. K. H., Ng E. Y. K., and Chiu W. S., Comparison of turbulence models in near wake of transport plane C-130H fuselage, Journal of Aircraft. (2013) 50, no. 3, 847–852, https://doi.org/10.2514/1.c032031, 2-s2.0-84880939967.
10.2514/1.C032031
Web of Science® Google Scholar
3 Zhang J. X., Xu H. J., Zhang D. C., and Liu D. L., Safety modeling and simulation of multi-factor coupling heavy-equipment airdrop, Chinese Journal of Aeronautics. (2014) 27, no. 5, 1062–1069, https://doi.org/10.1016/j.cja.2014.08.014, 2-s2.0-84922564116.
10.1016/j.cja.2014.08.014
Web of Science® Google Scholar
4 Chen J. and Shi Z. K., Aircraft modeling and simulation with cargo moving inside, Chinese Journal of Aeronautics. (2009) 22, no. 2, 191–197, https://doi.org/10.1016/s1000-9361(08)60086-2, 2-s2.0-64849087588.
10.1016/S1000-9361(08)60086-2
CAS Web of Science® Google Scholar
5 Raissi K., Mani M., Sabzehparvar M., and Ghaffari H., A single heavy load airdrop and its effect on a reversible flight control system, Aircraft Engineering and Aerospace Technology. (2008) 80, no. 4, 400–407, https://doi.org/10.1108/00022660810882764, 2-s2.0-47249125261.
10.1108/00022660810882764
Web of Science® Google Scholar
6 Liu R., Sun X. X., Dong W. H., Wang D., and Chang Y. G., Dynamics modeling and L₁ adaptive control of a transport aircraft for heavyweight airdrop, Mathematical Problems in Engineering. (2015) 2015, 15, 365130, https://doi.org/10.1155/2015/365130.
10.1155/2015/365130
Web of Science® Google Scholar
7 Feng Y. L., Shi Z. K., and Tang W., Dynamics modeling and control of large transport aircraft in heavy cargo extraction, Journal of Control Theory and Applications. (2011) 9, no. 2, 231–236, https://doi.org/10.1007/s11768-011-9099-1, MR2835115, 2-s2.0-79958236559.
10.1007/s11768-011-9099-1
Google Scholar
8 Xu G.-Z. and Sun X.-X., Heavyweight airdrop pitch flight control law design based on feedback linearization theory and variable structure control, Proceedings of the 6th IEEE Chinese Guidance, Navigation and Control Conference (CGNCC ’14), August 2014, Yantai, China, 962–967, https://doi.org/10.1109/cgncc.2014.7007339, 2-s2.0-84922553258.
10.1109/cgncc.2014.7007339
Google Scholar
9 Huiyuan Z. and Zhongke S., Variable structure control of catastrophic course in airdropping heavy cargo, Chinese Journal of Aeronautics. (2009) 22, no. 5, 520–527, https://doi.org/10.1016/s1000-9361(08)60135-1, 2-s2.0-70350507092.
10.1016/S1000-9361(08)60135-1
Web of Science® Google Scholar
10 Liu R., Sun X. X., and Dong W. H., Dynamics modeling and control of a transport aircraft for ultra-low altitude airdrop, Chinese Journal of Aeronautics. (2015) 28, no. 2, 478–487, https://doi.org/10.1016/j.cja.2015.02.008.
10.1016/j.cja.2015.02.008
Web of Science® Google Scholar
11 Yang Y. and Lu Y. P., Backstepping sliding mode control for super-low altitude heavy cargo airdrop from transport plane, Acta Aeronautica et Astronautica Sinica. (2012) 33, no. 12, 2301–2312, 2-s2.0-84872581846.
Google Scholar
12 Zhang J., Yang L. Y., and Shen G. Z., Modeling and attitude control of aircraft with center of gravity variations, Proceedings of the IEEE Aerospace Conference, March 2009, Big Sky, Mont, USA, IEEE, 1–11, https://doi.org/10.1109/aero.2009.4839615, 2-s2.0-70349149064.
10.1109/aero.2009.4839615
Google Scholar
13 Yang X. K., Zhong Y. W., Yang L., Zhang J., and Shen G. Z., Modeling and attitude control of aircraft with variations in mass and center of gravity, Proceedings of the 8th World Congress on Intelligent Control and Automation (WCICA ’10), July 2010, Jinan, China, IEEE, 323–329, https://doi.org/10.1109/wcica.2010.5555179, 2-s2.0-77958127356.
10.1109/wcica.2010.5555179
Google Scholar
14 Kotta Ü., Tõnso M., Shumsky A. Y., and Zhirabok A. N., Feedback linearization and lattice theory, Systems & Control Letters. (2013) 62, no. 3, 248–255, https://doi.org/10.1016/j.sysconle.2012.11.014, 2-s2.0-84872386817.
10.1016/j.sysconle.2012.11.014
Web of Science® Google Scholar
15 da Costa R. R., Chu Q. P., and Mulder J. A., Reentry flight controller design using nonlinear dynamic inversion, Journal of Spacecraft and Rockets. (2003) 40, no. 1, 64–71, https://doi.org/10.2514/2.3916, 2-s2.0-0037284889.
10.2514/2.3916
Web of Science® Google Scholar
16 Sieberling S., Chu Q. P., and Mulder J. A., Robust flight control using incremental nonlinear dynamic inversion and angular acceleration prediction, Journal of Guidance, Control, and Dynamics. (2010) 33, no. 6, 1732–1742, https://doi.org/10.2514/1.49978, 2-s2.0-78149232664.
10.2514/1.49978
Web of Science® Google Scholar
17 Choi I. H. and Bang H. C., Quadrotor-tracking controller design using adaptive dynamic feedback-linearization method, Proceedings of the Institution of Mechanical Engineers G: Journal of Aerospace Engineering. (2014) 228, no. 12, 2329–2342, https://doi.org/10.1177/0954410013516251, 2-s2.0-84909619016.
10.1177/0954410013516251
Web of Science® Google Scholar
18 Liu L. H., Zhu J. W., Tang G. J., and Bao W. M., Diving guidance via feedback linearization and sliding mode control, Aerospace Science and Technology. (2015) 41, 16–23, https://doi.org/10.1016/j.ast.2014.11.014, 2-s2.0-84920612441.
10.1016/j.ast.2014.11.014
CAS Web of Science® Google Scholar
19 Boiko I., Fridman L., Pisano A., and Usai E., Analysis of chattering in systems with second-order sliding modes, IEEE Transactions on Automatic Control. (2007) 52, no. 11, 2085–2102, https://doi.org/10.1109/tac.2007.908319, MR2361803, 2-s2.0-38149032411.
10.1109/TAC.2007.908319
Web of Science® Google Scholar
20 Levant A., Chattering analysis, IEEE Transactions on Automatic Control. (2010) 55, no. 6, 1380–1389, https://doi.org/10.1109/tac.2010.2041973, MR2668945, 2-s2.0-77953091999.
10.1109/TAC.2010.2041973
Web of Science® Google Scholar
21 Boiko I. M., Analysis of chattering in sliding mode control systems with continuous boundary layer approximation of discontinuous control, Proceedings of the American Control Conference (ACC ’11), June-July 2011, San Francisco, Calif, USA, IEEE, 757–762, https://doi.org/10.1109/ACC.2011.5990793.
10.1109/ACC.2011.5990793
Google Scholar
22 Wang H. Q., Chen B., and Lin C., Adaptive neural control for strict-feedback stochastic nonlinear systems with time-delay, Neurocomputing. (2012) 77, 267–274.
10.1016/j.neucom.2011.08.020
Web of Science® Google Scholar
23 Sonneveldt L., Chu Q. P., and Mulder J. A., Nonlinear flight control design using constrained adaptive backstepping, Journal of Guidance, Control, and Dynamics. (2006) 30, no. 2, 322–336, https://doi.org/10.2514/1.25834, 2-s2.0-33947619062.
10.2514/1.25834
Web of Science® Google Scholar
24 Hu J. C. and Zhang H. H., Immersion and invariance based command-filtered adaptive backstepping control of VTOL vehicles, Automatica. (2013) 49, no. 7, 2160–2167, https://doi.org/10.1016/j.automatica.2013.03.019, MR3063072, 2-s2.0-84878867972.
10.1016/j.automatica.2013.03.019
Web of Science® Google Scholar
25 Cong B. L., Liu X. D., and Chen Z., Backstepping based adaptive sliding mode control for spacecraft attitude maneuvers, Aerospace Science and Technology. (2013) 30, no. 1, 1–7, https://doi.org/10.1016/j.ast.2013.05.005, 2-s2.0-84885162986.
10.1016/j.ast.2013.05.005
Web of Science® Google Scholar
26 Farrell J., Sharma M., and Polycarpou M., Backstepping-based flight control with adaptive function approximation, Journal of Guidance, Control, and Dynamics. (2005) 28, no. 6, 1089–1102, https://doi.org/10.2514/1.13030, 2-s2.0-28444435207.
10.2514/1.13030
Web of Science® Google Scholar
27 Pomet J.-B. and Praly L., Adaptive nonlinear regulation: estimation from the Lyapunov equation, IEEE Transactions on Automatic Control. (1992) 37, no. 6, 729–740, https://doi.org/10.1109/9.256328, MR1164545, 2-s2.0-0026882722.
10.1109/9.256328
Web of Science® Google Scholar

Citing Literature

All articles

Projection-Based Adaptive Backstepping Control of a Transport Aircraft for Heavyweight Airdrop

Abstract

1. Introduction

2. Aircraft-Cargo Model with Cargo Extraction

3. Control Law and Stability Properties

3.1. Adaptive Backstepping Control Law

3.2. Stability Analysis

4. Simulation Analysis

5. Conclusions

Conflict of Interests

Acknowledgments

Appendix

Projection Operator

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Projection-Based Adaptive Backstepping Control of a Transport Aircraft for Heavyweight Airdrop

Abstract

1. Introduction

2. Aircraft-Cargo Model with Cargo Extraction

3. Control Law and Stability Properties

3.1. Adaptive Backstepping Control Law

3.2. Stability Analysis

4. Simulation Analysis

5. Conclusions

Conflict of Interests

Acknowledgments

Appendix

Projection Operator

References

Citing Literature

Figures

References

Related

Information