Volume 2015, Issue 1 358053

Research Article

Open Access

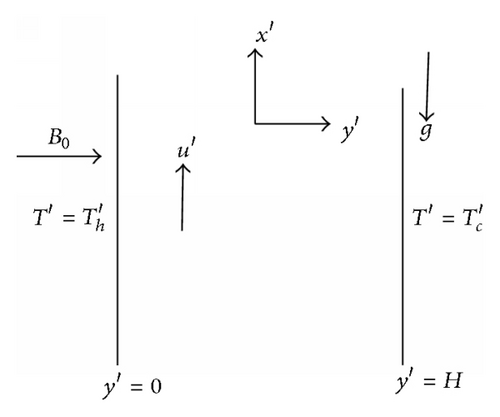
Unsteady/Steady Hydromagnetic Convective Flow between Two Vertical Walls in the Presence of Variable Thermal Conductivity

M. M. Hamza,

Corresponding Author

M. M. Hamza

[email protected]

Department of Mathematics, Usmanu Danfodiyo University, PMB 2346, Sokoto, Nigeria udusok.edu.ng

Search for more papers by this author

I. G. Usman,

I. G. Usman

Department of Mathematics, Zamfara State College of Education, PMB 1002, Maru, Nigeria

Search for more papers by this author

A. Sule,

A. Sule

Department of Mathematics, Zamfara State College of Education, PMB 1002, Maru, Nigeria

Search for more papers by this author

M. M. Hamza,

Corresponding Author

M. M. Hamza

[email protected]

Department of Mathematics, Usmanu Danfodiyo University, PMB 2346, Sokoto, Nigeria udusok.edu.ng

Search for more papers by this author

I. G. Usman,

I. G. Usman

Department of Mathematics, Zamfara State College of Education, PMB 1002, Maru, Nigeria

Search for more papers by this author

A. Sule,

A. Sule

Department of Mathematics, Zamfara State College of Education, PMB 1002, Maru, Nigeria

Search for more papers by this author

First published: 20 May 2015

https://doi.org/10.1155/2015/358053

Citations: 11

Academic Editor: Miguel Onorato

Share a link

Email
Wechat
Bluesky

Abstract

Unsteady as well as steady natural convection flow in a vertical channel in the presence of uniform magnetic field applied normal to the flow region and temperature dependent variable thermal conductivity is studied. The nonlinear partial differential equations governing the flow have been solved numerically using unconditionally stable and convergent semi-implicit finite difference scheme. For steady case, approximate solutions have been derived for velocity, temperature, skin friction, and the rate of heat transfer using perturbation series method. Results of the computations for velocity, temperature, skin friction, and the rate of heat transfer are presented graphically and discussed quantitatively for various parameters embedded in the problem. An excellent agreement was found during the numerical computations between the steady-state approximate solutions and unsteady numerical solutions at steady-state time. In addition, comparison with previously published work is performed and the results agree well.

1. Introduction

In recent years, the interest in the study of hydromagnetic flow in a channel region has been growing rapidly because of its extensive engineering applications. The experimental investigation of modern MHD flow in a laboratory was first carried out by [1]. This study provided the basic knowledge for the development of many MHD devices, such as MHD pumps, MHD generators, brakes, flow meters, plasma studies, and geothermal energy extraction. Unsteady free convection heat transfer with MHD effects in a channel region can be found in [2]. Unsteady hydromagnetic flows in rotating systems have been studied by [3–9]. An exact solution for unsteady hydromagnetic free convection flow with constant heat flux is to be found in [10]. All the above mentioned studies assumed the thermal conductivity of the fluid to be constant. However, it is known that the fluid physical properties may change significantly with temperature changes. To accurately predict the flow behavior and heat transfer rate, it is necessary to take into account the variation of thermal conductivity with temperature (see [11]). Thermal properties, particularly thermal conductivity and diffusivity, are essential materials parameters of bedrock controlling the heat transfer and temperature increases in the vicinity of repository. There has been considerable published work dealing with steady flow with variable thermal conductivity (see [12–18]). Recently (see [19]) studied steady MHD flow with variable thermal conductivity over an inclined radiative isothermal permeable surface.

To the best of our knowledge, the problem of unsteady/steady hydromagnetic convective flow between two vertical walls heated symmetrically/asymmetrically in the presence of variable thermal conductivity has not been studied. The present paper is committed to study unsteady as well as steady natural convection flow of a viscous, incompressible fluid between two parallel vertical walls in the presence of transverse magnetic field and temperature dependent variable thermal conductivity when convection between the vertical parallel walls is set up by a change in the temperature of the walls compared to the fluid temperature.

2. Governing Equations

Consider the unsteady natural convection flow of viscous, incompressible, and electrically conducting fluid between two vertical walls in the presence of a transversely imposed magnetic field of strength B₀. Initially, it is assumed that both the fluid and the walls are at rest and at the same temperature

. At time t^′ > 0, the temperature of the walls y^′ = 0 and y^′ = H is instantaneously raised or lowered to

and

, respectively, such that

which is thereafter maintained constant. We chose a Cartesian coordinate system with x^′ axis along the upward direction and the y^′ axis normal to it as shown in Figure 1. Thermal conductivity (k_f) of the fluid is assumed to vary as a linear function of temperature in the form (see [20]),

, where k_m is the fluid free stream thermal conductivity and δ is a constant depending on the nature of the fluid, where δ > 0 for fluids such as water and air, while δ < 0 for fluids such as lubrication oils (see [20]). The governing equations under Boussinesq’s approximation can be written as

()

The initial and boundary conditions for the present problem are

()

where β is the coefficient of the thermal expansion, ν is the kinematic viscosity, g is the gravitational force, σ is the conductivity of the fluid, B₀ is the electromagnetic induction, ρ is the density of the fluid, and c_p is the specific heat at constant pressure.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Geometry of the problem.

In order to solve (1) to (2), we employ the following dimensionless parameters:

()

Using (3), (1) to (2) can take the following form:

()

The initial and boundary conditions in dimensionless form are

()

3. Approximate Solutions

The approximated solutions played an important role in validating and exploring computer routes of complicated problems. Therefore, we reduce the governing equations of this problem due to its nonlinearity into a form that can be solved analytically. By setting ∂u/∂t = 0, and ∂θ/∂t = 0 into (4), we get

()

The boundary conditions are

()

In order to construct an approximate solution to (6) and (7) subject to (8), we employed a regular perturbation method by taking a power series expansion in the variable thermal conductivity parameter λ:

()

Substituting (9) into (6) to (8), the solution of the governing equations are obtained as

()

Using (10), we write the steady-state skin friction and rate of heat transfer on the boundaries as follows.

Steady-state skin friction on the boundary plates is

()

The steady-state rate of heat transfer on the boundary plates is

()

where

()

4. Numerical Solutions

The complete forms of (4) are solved numerically using semi-implicit finite difference scheme. We used forward difference formulas for all time derivatives and approximate the spatial derivatives with central difference formula. The semi-implicit finite difference equations corresponding to (4) are as follows:

()

where r₁ = ξΔt/Δy², r₂ = (1 − ξ)Δt/Δy²,

, r₄ = λΔt/4Δy², and 0 ≤ ξ ≤ 1. We chose ξ = 1 so that we are free to choose larger time steps. The approximated solutions displayed in the previous section are used as a check on the accuracy and effectiveness of the numerical scheme. Also, in order to reconfirm accuracy of the scheme, the numerical results for velocity and temperature are compared with the approximated solutions. It has been found that numerical values of the velocity and temperature fields calculated from expressions (10) have matched very well with the numerical solutions obtained from expressions (14) at the steady-state time. See Figure 2 for the graph of the numerical solutions at steady-state and steady-state approximate solutions for velocity and temperature fields. Again, Figures 3 and 4 represent comparisons with the work of [21] when Pr = 0.71, M = 0, and λ = 0. It is clear that excellent agreement between the present numerical solutions and the approximated solutions of [21] exists.

5. Results and Discussion

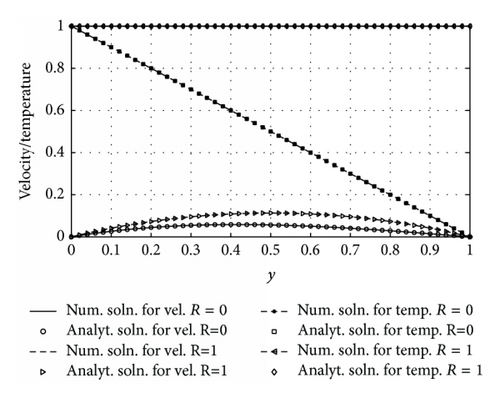
The numerical results are obtained by solving (14) using the method described in the previous section for various values of physical parameters to describe the physics of the problem. The nondimensional parameters that govern the flow are the Prandtl number (Pr), magnetic parameter (M), variable thermal conductivity parameter (λ), and buoyancy force distribution parameter (R). The value of Prandtl number (Pr) is taken as 1.0, which corresponds to electrolyte solution (see [22, 23]). Results obtained are presented graphically for velocity, temperature, skin friction, and Nusselt number for various flow parameters.

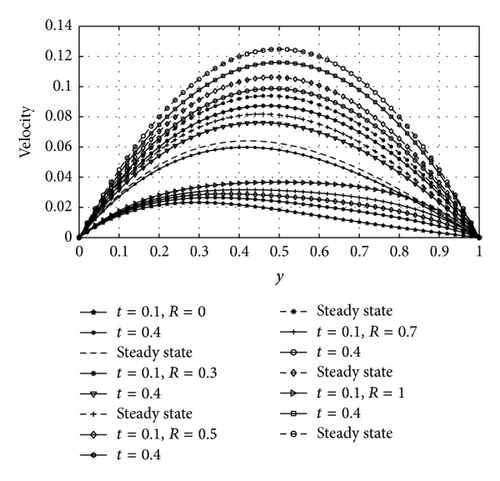
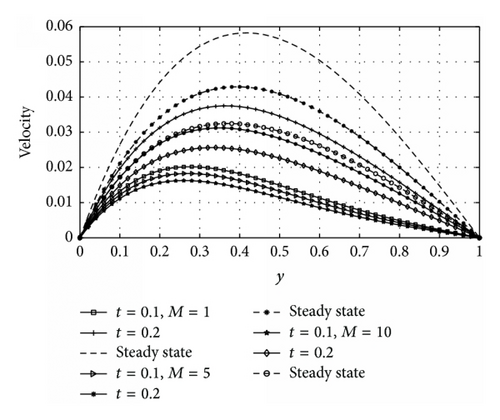
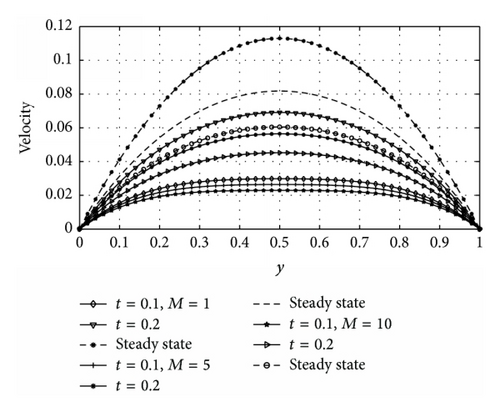
Figures 5 and 6 illustrate the velocity profiles of the fluid for different values of magnetic parameter (M) and nondimensional time (t) for asymmetric and symmetric case, respectively (i.e., R = 0 and R = 1). From Figure 5 it is observed that velocity of the fluid is maximum near the heated wall (y = 0) and then gradually decreases as it moves towards the cooled wall (y = 1). It is clear from Figure 6 that symmetric flow about occurs between the walls for all considered values of M and the nature of the figures is parabolic. In both Figures 5 and 6 it is noted that increasing M decreases the velocity of the flow throughout the channel walls. The physical explanation of this behavior is that the presence of magnetic field produces a resistivity force (Lorentz force) similar to the drag force which retard the velocity.

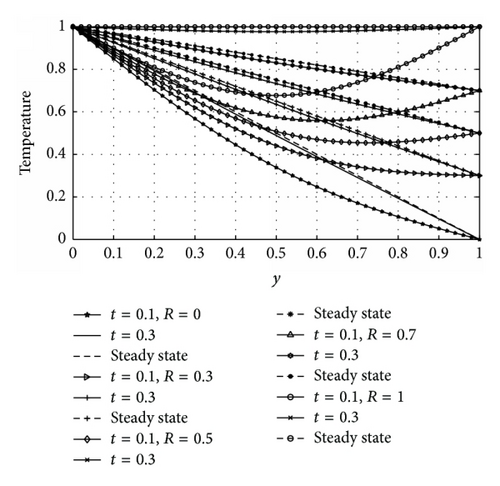
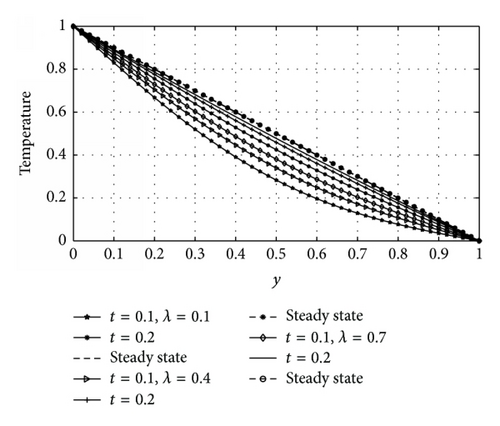
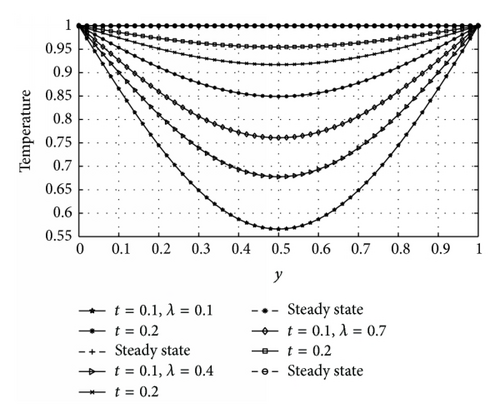
Figures 7 and 8, respectively, show the response of the fluid temperature to variation in the variable thermal conductivity parameter (λ) and time (t) for asymmetric and symmetric case. The effect of variable thermal conductivity (λ) and time (t) on velocity profiles for asymmetric and symmetric case is shown in Figures 9 and 10, respectively. From Figures 7 to 10, it is observed that both temperature and velocity of the fluid increase with increasing λ and t until a steady-state condition is attained. This is physically true, since the relation indicates that mounting values of λ increase the temperature difference between outside the plate and outside the boundary layer. As a result, heat is transferred rapidly from plate to fluid within the boundary layer. That is why both velocity and temperature profiles enlarge due to growing λ. It means that the velocity and the thermal boundary layer thickness rise for larger λ. From Figure 9, it is also seen that velocity of the fluid is maximum near the heated wall (y = 0) and then progressively decreases as it moves towards the cooled wall (y = 1). It is clear from Figures 8 and 10 that symmetric flow about occurs between the walls for all considered values of λ and t until a steady-state condition is achieved.

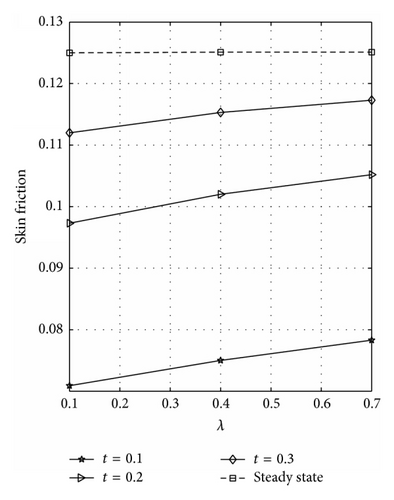
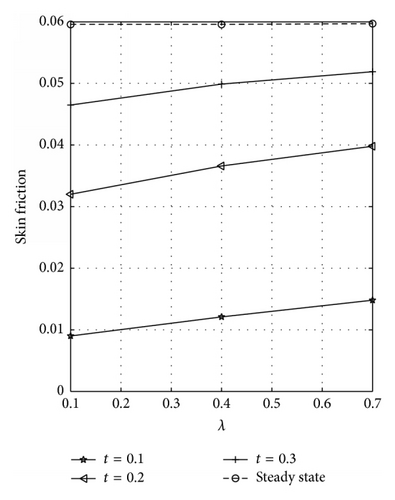
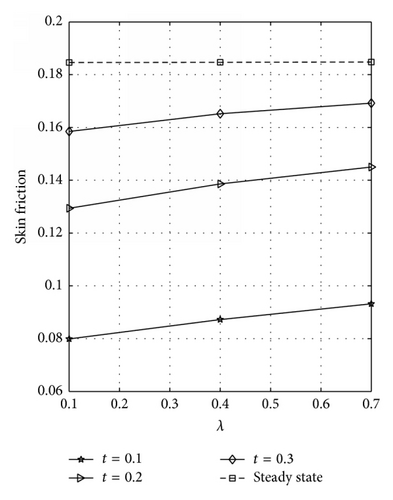
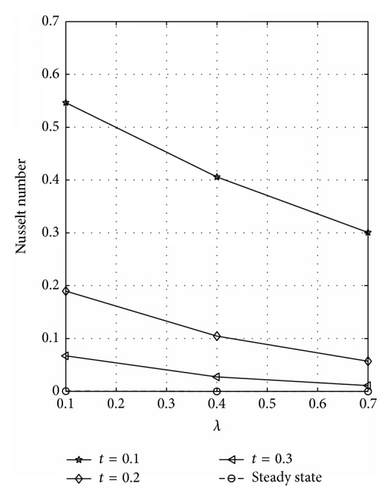
The rate of heat transfer (Nusselt number) dependence on λ is illustrated in Figure 11 for symmetric case. Figures 11(a) and 11(b) represent the rate of heat transfer at the walls y = 0 and y = 1, respectively. Figure 11(b) reveals that the rate of heat transfer increases as λ and t increase until a steady-state condition is reached. A reverse effect is observed at the plate y = 0; see Figure 11(a). The wall shear stress (skin friction) dependence on λ for varying values of t is illustrated in Figures 12(a) and 12(b) for symmetric case at the plates y = 0 and y = 1, respectively. From these figures, it is seen that skin friction increases with increase in λ and t. The skin friction and Nusselt number dependence on λ for varying values of t is displayed in Figures 13(a) and 13(b), respectively, at the plate y = 0 for asymmetric case. Figure 13(a) reflected that skin friction increases as λ and t increase until a steady-state condition is attained. Figure 13(b) reveals that Nusselt number decreases with increasing λ and t. It should be noted that the numerical values of skin friction at the plates y = 0 and y = 1 are the same for R = 1 because a symmetric flow occurs for this case. Also, the Nusselt number at the plates y = 0 and y = 1 is the same for R = 1.

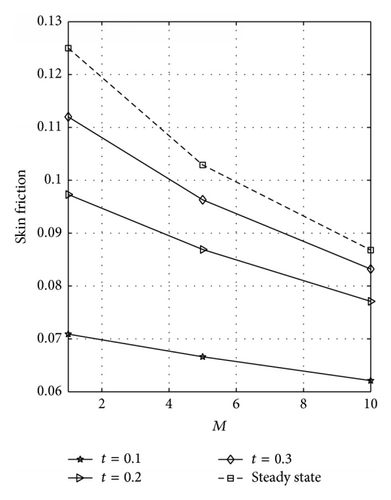
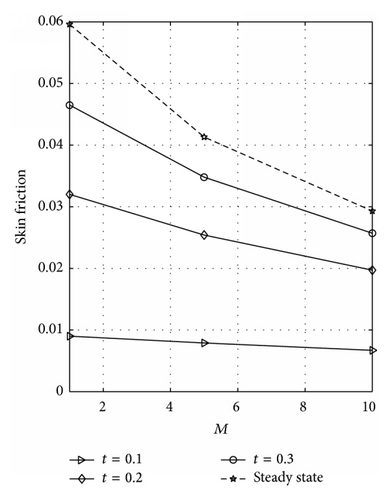
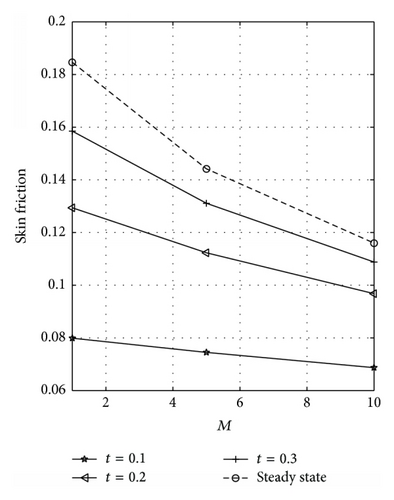
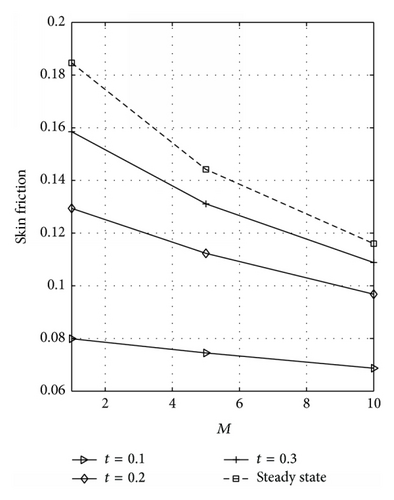
The skin friction dependence on M for varying values of t at the plates y = 0 and y = 1 is displayed in Figures 14(a) and 14(b), respectively, for R = 0. These figures reflected that skin friction decreases as M and t increase. Figures 15(a) and 15(b) are plotted to see the effects of M on the skin friction at the plates y = 0 and y = 1 for R = 1. From these figures, it is observed that skin friction decreases as M and t increase. Further, it is noted that Figures 15(a) and 15(b) are exactly the same. This is because a symmetric flow occurs for this case; that is, R = 1.

6. Conclusion

The problem of unsteady as well as steady hydromagnetic natural convection flow of a viscous, incompressible, and electrically conducting fluid between two vertical walls having asymmetric/symmetric temperatures on the walls in the presence of variable thermal conductivity and uniform applied magnetic field has been studied by obtaining approximated and numerical solutions of the governing equations, using perturbation series method and semi-implicit finite difference scheme. It is found that the fluid velocity and temperature increase with the increasing of variable thermal conductivity and nondimensional time for both asymmetric and symmetric heating, while magnetic parameter retards the motion of the fluid.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Hartmann J. and Lazarus F., Hg-dynamics II: ‘theory of laminar flow of electrically conductive liquids in a homogeneous magnetic field’, Matematisk-Fysiske Meddelelser. (1937) 15, no. 7.
Google Scholar
2 Singer R. M., Transient magnetohydrodynamic flow and heat transfer, Zeitschrift für angewandte Mathematik und Physik. (1965) 16, no. 4, 483–494, https://doi.org/10.1007/bf01593924, 2-s2.0-34250604172.
10.1007/BF01593924
Web of Science® Google Scholar
3 Seth G. S. and Jana R. N., Unsteady hydromagnetic flow in a rotating channel with oscillating pressure gradient, Acta Mechanica. (1980) 37, no. 1-2, 29–41, https://doi.org/10.1007/BF01441241, MR579497, ZBL0434.76094, 2-s2.0-0018925970.
10.1007/BF01441241
Web of Science® Google Scholar
4 Seth G. S., Jana R. N., and Maiti M. K., Unsteady hydromagnetic couette flow in a rotating system, International Journal of Engineering Science. (1982) 20, no. 9, 989–999, https://doi.org/10.1016/0020-7225(82)90034-9, 2-s2.0-0020012980.
10.1016/0020-7225(82)90034-9
Web of Science® Google Scholar
5 Seth G. S. and Ghosh S. K., Unsteady hydromagnetic flow in a rotating channel in the presence of inclined magnetic field, International Journal of Engineering Science. (1986) 24, no. 7, 1183–1193, https://doi.org/10.1016/0020-7225(86)90013-3, 2-s2.0-0022602420.
10.1016/0020-7225(86)90013-3
Web of Science® Google Scholar
6 Chandran P., Sacheti N. C., and Singh A. K., Effect of rotation on unsteady hydromagnetic Couette flow, Astrophysics and Space Science. (1993) 202, no. 1, 1–10, https://doi.org/10.1007/BF00626910, ZBL0774.76094, 2-s2.0-24944522348.
10.1007/BF00626910
Web of Science® Google Scholar
7 Singh A. K., Sacheti N. C., and Chandran P., Transient effects on magnetohydrodynamic couette flow with rotation: accelerated motion, International Journal of Engineering Science. (1994) 32, no. 1, 133–139, https://doi.org/10.1016/0020-7225(94)90155-4, 2-s2.0-0028336133.
10.1016/0020-7225(94)90155-4
CAS Web of Science® Google Scholar
8 Jha B. K. and Apere C. A., Combined effect of hall and ion-slip currents on unsteady MHD couette flows in a rotating system, Journal of the Physical Society of Japan. (2010) 79, 9, 104401, https://doi.org/10.1143/jpsj.79.104401, 2-s2.0-77958052023.
10.1143/JPSJ.79.104401
Web of Science® Google Scholar
9 Jha B. K. and Apere C. A., Magnetohydrodynamic free convective Couette flow with suction and injection, Journal of Heat Transfer. (2011) 133, no. 9, 12, 092501, https://doi.org/10.1115/1.4003902, 2-s2.0-79961174960.
10.1115/1.4003902
Web of Science® Google Scholar
10 Sacheti N. C., Chandran P., and Singh A. K., An exact solution for unsteady magnetohydrodynamic free convection flow with constant heat flux, International Communications in Heat and Mass Transfer. (1994) 21, no. 1, 131–142, https://doi.org/10.1016/0735-1933(94)90090-6, 2-s2.0-0028174731.
10.1016/0735-1933(94)90090-6
Web of Science® Google Scholar
11 Hossain M. A., Khanafer K., and Vafai K., The effect of radiation on free convection flow of fluid with variable viscosity from a porous vertical plate, International Journal of Thermal Sciences. (2001) 40, no. 2, 115–124, https://doi.org/10.1016/s1290-0729(00)01200-x, 2-s2.0-0035255487.
10.1016/S1290-0729(00)01200-X
CAS Web of Science® Google Scholar
12 Arunachalam M. and Rajappa N. R., Forced convection in liquid metals with variable thermal conductivity and capacity, Acta Mechanica. (1978) 31, no. 1-2, 25–31, https://doi.org/10.1007/BF01261185, ZBL0398.76066, 2-s2.0-0018048858.
10.1007/BF01261185
Web of Science® Google Scholar
13 Chiam T. C., Heat transfer with variable conductivity in a stagnation-point flow towards a stretching sheet, International Communications in Heat and Mass Transfer. (1996) 23, no. 2, 239–248, https://doi.org/10.1016/0735-1933(96)00009-7, 2-s2.0-0030088174.
10.1016/0735-1933(96)00009-7
Web of Science® Google Scholar
14 Chiam T. C., Heat transfer in a fluid with variable thermal conductivity over a linearly stretching sheet, Acta Mechanica. (1998) 129, no. 1-2, 63–72, https://doi.org/10.1007/BF01379650, ZBL0914.76026, 2-s2.0-0031652895.
10.1007/BF01379650
Web of Science® Google Scholar
15 Seddeek M. A. and Salem A. M., Laminar mixed convection adjacent to vertical continuously stretching sheets with variable viscosity and variable thermal diffusivity, Heat and Mass Transfer. (2005) 41, no. 12, 1048–1055, https://doi.org/10.1007/s00231-005-0629-6, 2-s2.0-28144464864.
10.1007/s00231-005-0629-6
CAS Web of Science® Google Scholar
16 Rahman M. M., Mamun A. A., Azim M. A., and Alim M. A., Effects of temperature dependent thermal conductivity on magnetohydrodynamic free convection flow along a vertical flat plate with heat conduction, Nonlinear Analysis: Modelling and Control. (2008) 13, 513–524, Zbl1163.35462.
10.15388/NA.2008.13.4.14555
Web of Science® Google Scholar
17 Sharma P. R. and Singh G., Effects of variable thermal conductivity and heat source/sink on MHD flow near a stagnation point on a linearly stretching sheet, Journal of Applied Fluid Mechanics. (2009) 2, no. 1, 13–21, 2-s2.0-59549084027.
Web of Science® Google Scholar
18 Alim M. A., Karim M. R., and Akand M. M., Heat generation effects on MHD natural convection flow along a vertical wavy surface with variable thermal conductivity, American Journal of Computational Mathematics. (2012) 2, no. 1, 42–50, https://doi.org/10.4236/ajcm.2012.21005.
10.4236/ajcm.2012.21005
Google Scholar
19 Reddy M. G., Effects of thermophoresis, viscous dissipation and joule heating on steady MHD flow over an inclined radiative isothermal permeable surface with variable thermal conductivity, Journal of Applied Fluid Mechanics. (2014) 7, no. 1, 51–61, 2-s2.0-84892645591.
Web of Science® Google Scholar
20 Elbarbary E. M. E. and Elgazery N. S., Chebyshev finite difference method for the effects of variable viscosity and variable thermal conductivity on heat transfer from moving surfaces with radiation, International Journal of Thermal Sciences. (2004) 43, no. 9, 889–899, https://doi.org/10.1016/j.ijthermalsci.2004.01.008, 2-s2.0-3142680927.
10.1016/j.ijthermalsci.2004.01.008
Web of Science® Google Scholar
21 Singh A. K. and Paul T., Transient natural convection between two vertical walls heated/cooled asymmetrically, International Journal of Applied Mechanics and Engineering. (2006) 11, 143–154.
Google Scholar
22 Ettefagh J., Vafai K., and Kim S. J., Non-Darcian effects in open-ended cavities filled with a porous medium, Journal of Heat Transfer. (1991) 113, no. 3, 747–756, https://doi.org/10.1115/1.2910627, 2-s2.0-0026206454.
10.1115/1.2910627
CAS Web of Science® Google Scholar
23 Alazmi B. and Vafai K., Analysis of variants within the porous media transport models, Journal of Heat Transfer. (2000) 122, no. 2, 303–326, https://doi.org/10.1115/1.521468, 2-s2.0-0033847786.
10.1115/1.521468
Web of Science® Google Scholar

Citing Literature

All articles

Unsteady/Steady Hydromagnetic Convective Flow between Two Vertical Walls in the Presence of Variable Thermal Conductivity

Abstract

1. Introduction

2. Governing Equations

3. Approximate Solutions

4. Numerical Solutions

5. Results and Discussion

6. Conclusion

Conflict of Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Unsteady/Steady Hydromagnetic Convective Flow between Two Vertical Walls in the Presence of Variable Thermal Conductivity

Abstract

1. Introduction

2. Governing Equations

3. Approximate Solutions

4. Numerical Solutions

5. Results and Discussion

6. Conclusion

Conflict of Interests

References

Citing Literature

Figures

References

Related

Information