The combined effect of surface roughness and magnetic field on the performance characteristic of the circular plates lubricated with conducting couplestress fluid (CCSF) has been studied. On the basis of the Christensen Stochastic model, the generalized stochastic Reynold’s equation is derived. Modified equations for the nondimensional pressure, load load-carrying capacity, and squeeze film time are derived. The results are presented both numerically and graphically and compared with conducting smooth surface case. It is observed that the surface roughness effects are more pronounced for couplestresses as compared to nonconducting Newtonian fluid (NCNF) in the presence of magnetic field.

1. Introduction

In recent years, the characteristics of Magnetohydrodynamics (MHD) in flow analysis are important for many engineering and industrial applications. The MHD bearings with conducting fluids possess the high thermal-conductivity and high electrical-conductivity features over the conventional bearings. The squeeze film lubrication for different configuration of bearings under the action of transverse magnetic field has been discussed by several authors [1–6]. Stochastic model for hydrodynamic lubrication of rough surfaces is studied by Christensen [7]. The combined effect of MHD and surface roughness has been studied by many authors [8–11] and it is found that effect of surface roughness in the presence of transverse magnetic field is significant on the squeeze film characteristics of the bearings.

It is known that the theory of couplestress fluid by Stokes [12] is a generalization of viscous fluid theory with couplestresses and body couples. Couplestress fluids are consequence of the assumption that the interaction of one part of the body on another across a surface is equivalent to a force and momentum distribution. It consists of rigid randomly oriented particles suspended in a viscous medium such as electrorheological fluids and synthetic fluids. Many studies have investigated the effect of couplestress on the squeeze film lubrication in the presence of transverse magnetic field [13–15]. The MHD bearings with conducting fluids possess numerous advantages over the conventional bearings.

Recently, Lin et al., [16] studied hydromagnetic non-Newtonian cylindrical squeeze film and its application to circular plates by derivation of modified lubrication equation. They found that the improved characteristics are further emphasized for circular plates operating with a larger magnetic field parameter and non-Newtonian parameter.

The effect of surface roughness on MHD conducting couplestress squeeze-film characteristics between the circular plates has not been studied so far. Hence, in this paper, an attempt has been made to study the combined effect of surface roughness and conducting couplestresses on the MHD squeeze-film characteristics between circular plates. Expressions for the MHD squeeze-film pressure, load carrying capacity, and the time height relation are obtained. Results are compared numerically with the corresponding conventional case for different values Hartmann number M₀ studied by Lin et al., [16].

2. Mathematical Formulation of the Problem

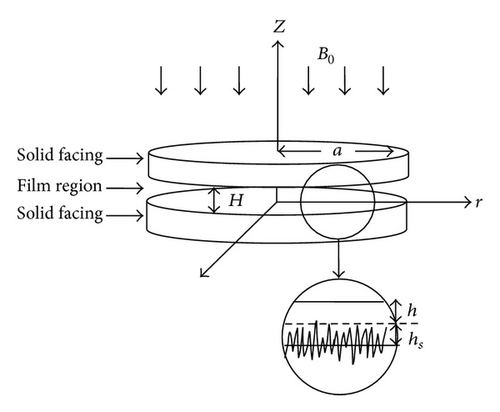
Consider a squeezing flow between two rough circular plates approaching each other with squeezing velocity V ( = dH/dt), where H is the film thickness between the two plates, p is the film pressure, u and w are the velocity components, μ is the lubricant viscosity, η is material constant responsible for couplestresses, and σ is the conductivity of the lubricant. A uniform transverse magnetic field is applied to the bearing in the Z-direction as shown in Figure 1. It is assumed that the fluid film is thin and the body forces and the body couples are negligible. The third term in (1) is a Lorentz body force coming from J_yB₀ under the assumption that the induced magnetic field is much less than the applied magnetic field as described by Kuzma [17]. Then, from Ohm’s law, the axial current density becomes J_y = σB₀u. Therefore, the term appears in (1).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The physical configuration of rough circular plates in the presence of transverse magnetic field.

Under the usual assumption of hydromagnetic lubrication theory applicable to thin films and Stokes theory for couplestresses, the continuity equation and the Magnetohydrodynamic (MHD) momentum equations in polar form becomes

()

The relevant boundary conditions for the velocity components are as follows.

(1)
At the lower surface, z = 0

()

(2)
At the upper surface, z = H

()

The expressions for the radial component can be obtained by solving (1) subject to boundary conditions (4a) to (5c) we get

()

where h₀ is the initial film thickness, l ( = (η/μ) ^1/2) is the couplestress parameter characterizing the non-Newtonian effects, M₀ ( = B₀h₀(σ/μ) ^1/2) is the Hartmann number measuring the strength of the magnetic field, and A and B are dimensional quantities that depend on l and M₀. Consider

()

The integral form of the continuity equation (3) across the film thickness is

()

Substituting the expression of u and applying the velocity boundary conditions, one can derive the modified Reynolds equation after performing the integration:

()

where

()

Let g(h_s) be the probability density function of the stochastic film thickness h_s.

Taking the stochastic average of (9) with respect to g(h_s), the averaged modified Reynolds type equation is obtained in the form

()

where

()

In accordance with Christensen [7], we assume that

()

where

is the standard deviation.

In context of Christensen stochastic theory for the hydrodynamic lubrication of rough surfaces, two roughness patterns are considered, namely, radial roughness pattern and azimuthal roughness pattern.

2.1. Radial Roughness Pattern

For the one-dimensional radial roughness pattern, the roughness structure has the form of long, narrow ridges and valleys running in the radial direction (i.e., they are straight ridges and valleys passing through z = 0 and r = 0). In this case, the film thickness takes the form

()

The stochastic modified Reynolds equation (11) takes the form

()

2.2. Azimuthal Roughness Pattern

For the one-dimensional azimuthal roughness, the bearing surfaces have the form of long narrow ridges and valleys running in the θ-direction (i.e., they are circular ridges and valleys on the flat plate that are concentric on z = 0 and r = 0). In this case, the film thickness assumes the form

()

The modified Reynolds type equation (11) takes the form

()

For an axisymmetric case, these equations reduce to

()

where

()

The relevant boundary conditions for the pressure field are

()

Solving (22) using the boundary conditions (23a) and (23b) gives

()

The dimensionless form of the film pressure is given by

()

where

()

The load carrying capacity of the squeeze film is obtained by integrating the pressure field over the area of the plate

()

The nondimensional mean instantaneous load carrying capacity W^* of the squeeze film is given by

()

For the constant load W, the time required for the film thickness to decrease to the value h₁ at time t₁ can be obtained by integrating (29). Hence,

()

where

3. Results and Discussions

The combined effect of surface roughness and MHD on the conducting couplestress fluid lubrication between circular plates is analysed on basis of Christensen’s stochastic theory [7] for two types of roughness patterns. The squeeze film characteristics are analysed with respect to three nondimensional parameters, namely, the Hartmann number , conducting couplestress parameter l^*, and the roughness parameter C.

Figure 2 depicts the variation of nondimensional mean pressure P^* with the axial coordinate r as a function of the roughness parameter C with the parametric values M₀ = 3, l^* = 0.3, and H^* = 0.4 for both roughness patterns. It is observed that, at C = 0, the radial roughness pattern coincides with the azimuthal roughness pattern. Further, the increase in P^* is more pronounced with azimuthal roughness pattern as compared to radial roughness pattern. Figure 3 represents the variation of nondimensional load carrying capacity W^* with H^* for different values of l^*. It is observed that, with the increasing of values of l^*, there is significant increase in the load carrying capacity W^*. The effects are more prominent for CCSF as compared to conventional NCNF. Figure 4 shows the variation of nondimensional mean load carrying capacity W^* with H^* for different values of M₀. It is seen that increasing effect of M₀ is to enhance the mean load carrying capacity for circular plates as compared to smooth plate case. Figure 5 shows the variation of nondimensional load W^* with H^* as a function of roughness parameter C with M₀ = 3 and l^* = 0.3. As seen from the figure that the load carrying capacity is significant with increasing values of roughness parameter and the effects are more prominent for azimuthal roughness pattern than those for radial roughness pattern. Variation on nondimensional squeeze film time T^* with for different values of l^* is shown in Figure 6. It is observed that, with the increasing of values of l^*, there is significant increase in squeeze film time T^*. The variation of response time T^* as function is given in Figure 7 for various values of M₀. It is observed that the effect of magnetic parameter is to enhance the squeezing effect for rough circular plates as compared to smooth plates. Figure 8 shows the variation on nondimensional squeeze film time T^* with for different values of C. It is observed that T^* increases with increasing values of C. The effects are more pronounced for CCSF as compared to NCNF. It is observed that the effect of azimuthal/radial roughness patterns is to increase/decrease T^* as compared to conventional case (i.e., C = 0). The time of approach is more pronounced for azimuthal roughness patterns as compared to the radial roughness pattern.

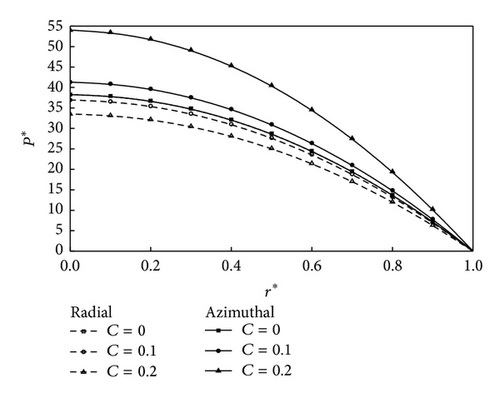
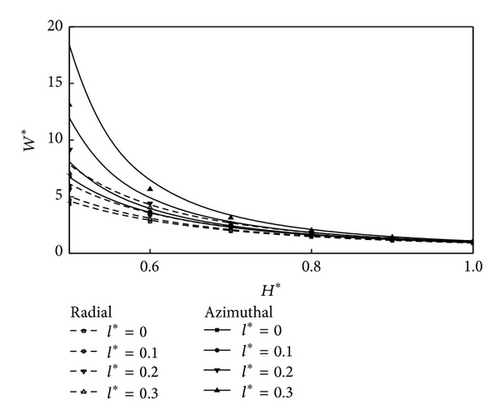
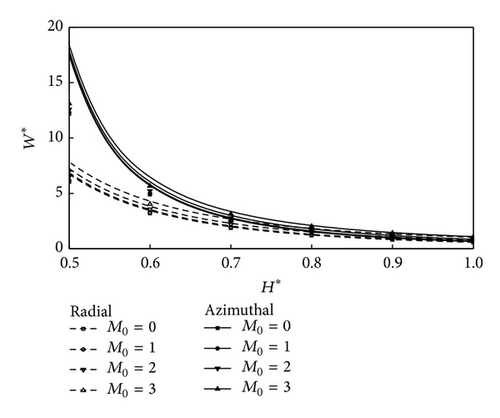
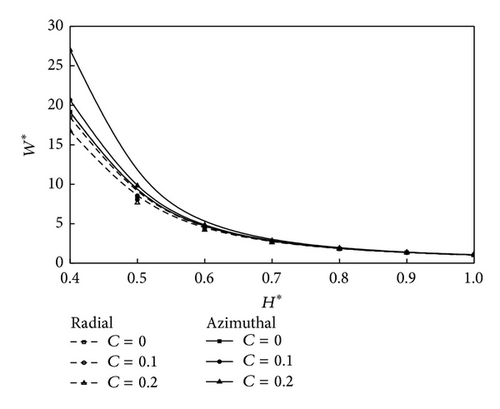
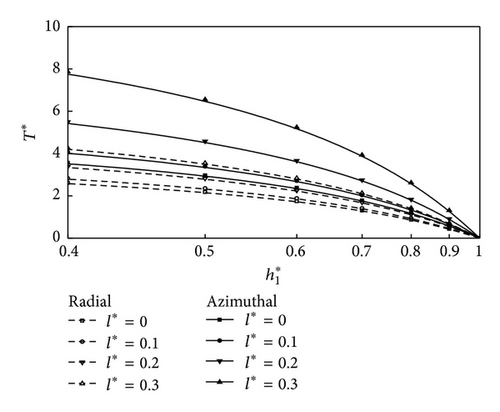
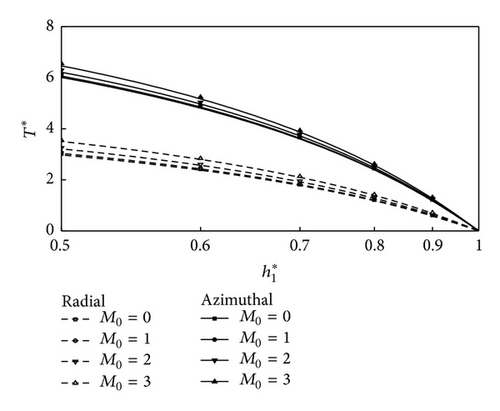
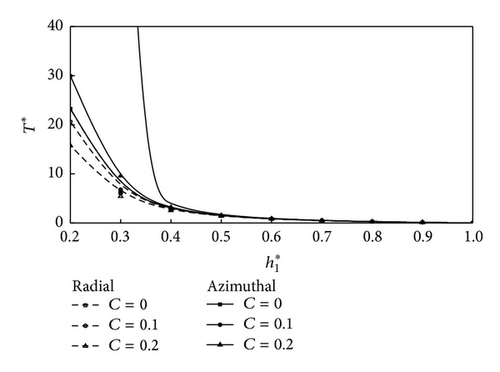
Table 1 shows the comparison between the previous analysis by Lin et al., [16] and the present analysis. It is observed from the table that there is significant increase in load and time for both the roughness patterns. An increase of 14.50%/52.28% in radial/azimuthal roughness pattern is observed for M₀ = 3, C = 0.3.

Table 1. Numerical comparison of load carrying capacity and the squeezing time between Lin et al., [16] and the present analysis with H^* = 0.4, l^* = 0.3, and

Nondimensional load carrying capacity W^*					Nondimensional squeezing time T^*
M₀	Lin et al. [16]	Present analysis			Lin et al. [16]	Present analysis
M₀	Lin et al. [16]	C = 0	C = 0.3 (radial)	C = 0.3 (azimuthal)	Lin et al. [16]	C = 0	C = 0.3 (radial)	C = 0.3 (azimuthal)
0	18.0346	18.0345	13.068	51.1056	1.1262	1.1262	1.00394	1.51557
1	18.1567	18.1566	13.2377	51.2369	1.15996	1.15996	1.04196	1.55012
2	18.5232	18.5231	13.7416	51.6309	1.26118	1.26118	1.15448	1.65369
3	19.1338	19.1338	14.5654	52.2874	1.42968	1.42968	1.33827	1.82611

4. Conclusions

The combined effect of surface roughness and MHD on the conducting couplestress squeeze-film characteristics between circular plates is presented on the basis of Christensen stochastic theory for rough surfaces [7]. From the above theoretical and numerical results, the following conclusions can be drawn.

(i)
In the presence of a conducting couplestress fluid and externally applied transverse magnetic field, one-dimensional radial/azimuthal roughness patterns on the circular plates decrease/increase the load-carrying capacity and response time as compared to the nonconducting case.
(ii)
As the surface asperity increases, the large amount of load is delivered in the bearing and enhances the response time of squeeze-film motion as compared to the smooth case.
(iii)
In the limiting case, as C → 0, the result for both roughness patterns for one-dimensional circular plates can be reduced to smooth surface studied by Lin et al., [16] and the comparison is shown in Table 1.

Nomenclature

a :: Radius of the circular plates
B₀:: Applied magnetic field in the z-direction
c:: Maximum asperity deviation from the nominal film height
C:: Dimensionless roughness parameter (c/h₀)
H:: Film thickness
h₀:: Initial film thickness
h₁:: Film thickness at time t₁
:: Dimensionless film thickness after time Δt
h_s:: Stochastic film thickness
M₀:: Hartmann number ( = B₀h₀(σ/μ) ^1/2)
l:: Couplestress parameter (η/μ)^1/2
l^*:: Dimensionless couplestress parameter 2l/h₀
r, θ, z:: Radial, angular, and axial coordinates
u, v, w:: Velocity components in film region
E(P):: Pressure in the film region
P^*:: Dimensionless pressure
t:: Mean time of approach
T^*:: Dimensionless time of approach
V:: Squeezing velocity (−dH/dt)
W^*:: Dimensionless load carrying capacity .

Greek Symbols

σ:: Conductivity of fluid
:: Standard deviation
η:: Material constant responsible for couplestress
μ:: Lubricant viscosity
ξ:: Random variable.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Hughes W. F., The magnetohydrodynamic finite step slider bearing, Journal of Fluids Engingeering. (1963) 85, no. 1, 129–135.
Google Scholar
2 Hughes W. F. and Elco R. A., Magnetohydrodynamic lubrication flow between parallel rotating disks, Journal of Fluid Mechanics. (1962) 13, no. 1, 21–32, MR0140253, https://doi.org/10.1017/s0022112062000464.
10.1017/S0022112062000464
Web of Science® Google Scholar
3 Huzma D. C., The Magneto-hydrodynamic parallel slider bearing, Transactions of the ASME Journal of Fluids Engineering. Series D. (1965) 87, 778–780.
10.1115/1.3650685
Google Scholar
4 Kuzma D. C., Maki E. R., and Donnely R. J., The MHD squeeze film, Journal of Fluid Mechanics. (1964) 19, no. 3, 395–400, https://doi.org/10.1017/s0022112064000805.
10.1017/S0022112064000805
Web of Science® Google Scholar
5 Huges W. F. and Elco R. J., Magnetohydrodynamic journal bearing, Journal of American Rocket Society. (1962) 32, 776–778.
Google Scholar
6 Lin J.-R., Magneto-hydrodynamic squeeze film characteristics between annular disks, Industrial Lubrication and Tribology. (2001) 53, no. 2, 66–71, 2-s2.0-0035266159, https://doi.org/10.1108/00368790110384028.
10.1108/00368790110384028
Web of Science® Google Scholar
7 Christensen H., Stochastic models for hydrodynamic lubrication of rough surfaces, Proceedings of the Institution of Mechanical Engineers. (1969) 184, no. 55, 1013–1026, 2-s2.0-0014657077.
10.1243/PIME_PROC_1969_184_074_02
Google Scholar
8 Bujurke N. M. and Kudenatti R. B., MHD lubrication flow between rough rectangular plates, Fluid Dynamics Research. (2007) 39, no. 4, 334–345, https://doi.org/10.1016/j.fluiddyn.2006.05.004, MR2317213, 2-s2.0-33947193132.
10.1016/j.fluiddyn.2006.05.004
Web of Science® Google Scholar
9 Naduvinamani N. B., Fathima S. T., and Jamal S., Effect of roughness on hydromagnetic squeeze films between porous rectangular plates, Tribology International. (2010) 43, no. 11, 2145–2151, https://doi.org/10.1016/j.triboint.2010.06.002, 2-s2.0-77956184554.
10.1016/j.triboint.2010.06.002
CAS Web of Science® Google Scholar
10 Bujurke N. M., Naduvinamani N. B., and Basti D. P., Effect of surface roughness on magnetohydrodynamic squeeze film characteristics between finite rectangular plates, Tribology International. (2011) 44, no. 7-8, 916–921, https://doi.org/10.1016/j.triboint.2011.03.008, 2-s2.0-79955663284.
10.1016/j.triboint.2011.03.008
Web of Science® Google Scholar
11 Naduvinamani N. B. and Rajashekar M., Effect of surface roughness on magneto-hydrodynamic squeeze-film characteristics between a sphere and a porous plane surface, Industrial Lubrication and Tribology. (2014) 66, no. 3, 365–372, https://doi.org/10.1108/ilt-01-2012-0013, 2-s2.0-84901014273.
10.1108/ilt-01-2012-0013
Web of Science® Google Scholar
12 Stokes V. K., Couple stresses in fluids, Physics of Fluids. (1966) 9, no. 9, 1709–1715, https://doi.org/10.1063/1.1761925, 2-s2.0-36849106425.
10.1063/1.1761925
CAS Web of Science® Google Scholar
13 Lin J.-R., Chu L.-M., Hung C.-R., and Wang P.-Y., Derivation of two-dimensional couple-stress hydromagnetic squeeze film Reynolds equation and application to wide parallel rectangular plates, Meccanica. (2013) 48, no. 1, 253–258, https://doi.org/10.1007/s11012-012-9613-7, 2-s2.0-84870454611.
10.1007/s11012-012-9613-7
Web of Science® Google Scholar
14 Naduvinamani N. B., Fathima S. T., and Hanumagowda B. N., Magneto-hydrodynamic couplestress squeeze film lubrication of circular stepped plates, Journal of Engineering Tribology. (2011) 225, part I, 111–119, 2-s2.0-79960190047.
Google Scholar
15 Fathima S. T., Naduvinamani N. B., Marulappa S. H., and Bannihalli H., A study on the performance of hydromagnetic squeeze film between anisotropic porous rectangular plates with couplestress fluids, Tribology Online. (2014) 9, no. 1, 1–9, https://doi.org/10.2474/trol.9.1, 2-s2.0-84894309429.
10.2474/trol.9.1
Google Scholar
16 Lin J.-R., Chu L.-M., Liang L.-J., and Lee P.-H., Derivation of a modified lubrication equation for hydromagnetic non-Newtonian cylindrical squeeze films and its application to circular plates, Journal of Engineering Mathematics. (2012) 77, 69–75, https://doi.org/10.1007/s10665-012-9540-6, MR2990653, 2-s2.0-84867982332.
10.1007/s10665-012-9540-6
CAS Web of Science® Google Scholar
17 Kuzma D. C., Magnetohydrodynamic squeeze films, Journal of Fluids Engineering. (1964) 86, no. 3, 441–444, https://doi.org/10.1115/1.3653131.
10.1115/1.3653131
Google Scholar

Citing Literature

All articles

Effect of Surface Roughness on the Squeeze Film Characteristics of Circular Plates in the Presence of Conducting Couplestress Fluid and Transverse Magnetic Field

Abstract

1. Introduction