The development of a control strategy appropriate for the suppression of aeroelastic vibration of a two-dimensional nonlinear wing section based on iterative learning control (ILC) theory is described. Structural stiffness in pitch degree of freedom is represented by nonlinear polynomials. The uncontrolled aeroelastic model exhibits limit cycle oscillations beyond a critical value of the free-stream velocity. Using a single trailing-edge control surface as the control input, a ILC law under alignment condition is developed to ensure convergence of state tracking error. A novel Barrier Lyapunov Function (BLF) is incorporated in the proposed Barrier Composite Energy Function (BCEF) approach. Numerical simulation results clearly demonstrate the effectiveness of the control strategy toward suppressing aeroelastic vibration in the presence of parameter uncertainties and triangular, sinusoidal, and graded gust loads.

1. Introduction

Aeroelasticity is the field of study that deals with the interaction of structural, inertial, and aerodynamic loads. When combined, these loads may encounter adverse instabilities, such as flutter. Within classic aeroelastic theories, linear assumptions are made for the aerodynamics and the structures, and the aeroelastic problem is usually reduced to the straightforward solution of linear coupled equations [1]. However, the assumption of a linear and known structure, as well as the often oversimplified aerodynamic model, usually leads to inaccurate results.

In many cases, transonic dip, flow separation, and dynamic stall can introduce aerodynamic phenomena that classical aeroelasticity is unable to handle. One example is the transonic dip that linear aerodynamics cannot detect. In addition, flow separation and shock oscillations are beyond the capability of classic aeroelasticity [2]. Nonlinear aerodynamic effects are more difficult to analyze in a theoretical fashion, because the dynamics of flow is governed by the full potential, Euler, and Navier-Stokes formulations where analytical solutions are practically nonexistent [2, 3]. By contrast, structural nonlinearities arising from worn hinges of control surfaces, loose control linkages, and material behavior, as well as various other sources, can significantly complicate the wing dynamics. With structural nonlinearities, the aeroelastic system may exhibit various phenomena, including instability, limit cycle oscillations (LCOs), and chaotic vibration [4, 5]. This topic has been extensively analyzed and reviewed [2]. Wind tunnel experiments, primarily for a typical airfoil section and beam-like wings, can validate the results from numerical or theoretical schemes. In particular, Dowell and colleagues at Duke University [6, 7] and Ko and colleagues at Texas A&M University [8] have made several significant contributions. These researchers designed and installed an aeroelastic modeling with control surface freeplay and even created a periodic or a linear frequency sweep gust excitation in some experiments. Through these experimental facilities, a series of theoretical and experimental studies involving flutter and LCOs, as well as gust responses and alleviation, have been completed.

Several studies have focused on developing strategies to suppress flutter by active control. Control strategies to suppress flutter rely on the use of control surfaces, particularly for the two-dimensional wing section with structural stiffness nonlinearity. For example, a classical linear full-state feedback controller was developed, which guaranteed the wing section system with nonlinear stiffness to stabilize in some circumstances [9]. Bhoir and Singh designed a backstepping-based output feedback nonlinear control strategy for flutter suppression in [10]. Lee and Singh [11] proposed nonlinear controller for the aeroelastic system using L₁ adaptive feedback technique. The state-dependent Riccati equation method was developed for nonlinear control problems, which was used to design suboptimal control laws of nonlinear aeroelastic systems considering a quasi-steady and unsteady aeroelastic model [12, 13].

A considerable number of studies have dealt with the influence of uncertainty on aeroelastic response prediction. Pettit [14] briefly described general sources of uncertainty that complicate airframe design and testing. In particular, parametric uncertainty in nonlinear pitch stiffness has been modeled in the third- and fifth-order coefficients. Generally, uncertainties are specified in the cubic coefficient of the torsional spring and in the initial pitch angle of the airfoil. Beran et al. [15] applied standard probability concepts and Monte Carlo simulation to the study of the LCO of an airfoil with a nonlinear pitch spring. When the uncertainty was considered, adaptive controllers based on partial or full feedback linearization were derived, which were effective for flutter suppression [16]. Experimental results obtained using the adaptive control system were presented in [17], which verified the validity of the proposed method in [16]. Also, for a class of uncertain nonlinear multivariable systems, a higher-order sliding-mode control law for the finite-time control has been developed [18]. Motivated by the limited effectiveness of using a single control surface, improvements in the performance of the adaptive controller were investigated through multiple control surfaces [19]. An output feedback control law has been implemented to suppress flutter and adaptively compensate for uncertainties in all the aeroelastic model parameters [20]. In most of the available literature, only parametric uncertainty in pitch stiffness has been considered. The damping uncertainty in the airframe structure and control system is inevitable [21]. Li et al. [22] designed an adaptive control law for flutter suppression of a nonlinear aeroelastic system with damping uncertainty.

Recently, a new iterative learning control (ILC) theory has been developed for the control of uncertain nonlinear systems [23]. This design uses a Barrier Composite Energy Function (BCEF) method with a novel Barrier Lyapunov Function (BLF). The prerequisite for the ILC presented in the design is based on the alignment condition. This is different from Repetitive Control (RC) and merely requires the time to be reset. Nonetheless, in conventional ILC, a constant initial condition must be met in conventional ILC, that is, the time and state must be reset at the beginning of each iteration. This design approach has been applied for robotic manipulators and the other industrial control [24–28]. Several control systems for the prototypical wing section of Block and Strganac [9] have been designed in the past, but the application of ILC theory for this model has not been attempted. As such, it is of interest to develop an ILC flutter controller for the prototypical plunge-pitch 2D aeroelastic system in the presence of gust loads.

In this paper, the design of a control system for the stabilization of an aeroelastic system in the presence of parameter uncertainties and gust loads is considered. The design is based on ILC control theory. The model has pitch polynomial-type structural nonlinearities and describes the plunge and pitch motion of a wing section with a single control surface. The aeroelastic model has quasi-steady linear aerodynamics. A new ILC scheme is derived for a nonlinear system with both parametric and nonparametric uncertainties under alignment condition. A BLF is incorporated in the proposed BCEF approach. Under the proposed control scheme, uniform state tracking error convergence is guaranteed. Simulation results show that the controller suppresses the oscillatory motion of the system, despite uncertainties and triangular, exponential, and sinusoidal gust loads. The main contributions of this work are the following: (1) the authors present rigorous mathematical proof and simulation results utilizing the recently developed iterative learning control (ILC) theory as introduced in [23], (2) BLF is incorporated with BCEF to handle ILC problems under alignment condition, (3) both parametric and nonparametric nonlinear uncertainties can be handled by the proposed control scheme, and (4) compared to the conventional sliding mode control design, the proposed method has good performance in tracking the pitch angle and plunge displacement trajectories.

2. Aeroelastic Model and Control Problem

Figure 1 shows the aeroelastic model. A prototype of this model has been developed in [17]. The second-order differential equations governing the evolution of the pitch angle α (take the clockwise direction as positive) and the plunge displacement h (take the downward direction as positive) including the gust load are given by

(1)

where m_w is the mass of the wing section, m_t is the total mass, and b is the semichord of the wing. The parameter I_α is the moment of inertia, x_a is the nondimensionalized distance of the center of mass from the elastic axis, and c_α and c_h are the pitch and plunge damping coefficients, respectively. M and L are the aerodynamic moment and lift, respectively. Assuming a quasi-steady aerodynamic model, the aerodynamic lift and moment coefficients are expressed by

(2)

where a is the nondimensionalized distance from the midchord to the elastic axis; s_p is the span;

and

are the lift and moment coefficients per angle of attack, respectively;

and

are the lift and moment coefficients per control surface deflection β (take the clockwise direction as positive), respectively; and

and

are the effective dynamic and control moment derivatives, respectively.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Aeroelastic model.

The aerodynamic force and moment due to the wind gust is modelled as [29]

(3)

where w_G(τ) denotes the disturbance velocity and τ is a dimensionless time variable defined as τ = Ut/b.

The nonlinear function k_α(α) is considered a polynomial in α given by

(4)

where

is constant, n^′ = 5.

Equations (1) and (2) are combined to form the following compact state-space form:

(5)

where

(6)

Moreover,

In this study, with allowance for the uncertainty of stiffness parameters, formula (5) can be expressed as follows:

(7)

where g denotes the part containing known parameters; θ = (B^TB) ⁻¹B^Tθ^′ indicates the matrix related to nonlinear stiffness; and ξ represents the state vector of uncertain parameters, which is expressed as

(8)

and the system variables are as follows:

(9)

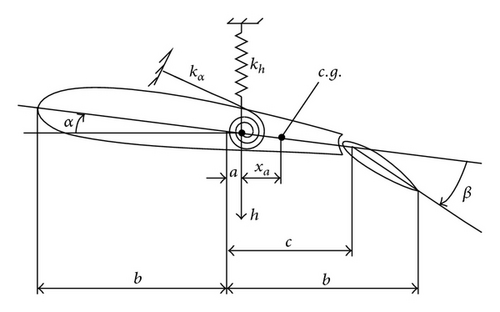
Based on the knowledge of the structure of the aeroelastic model, the control objective is to design a control strategy that drives the pitch angle α and plunge displacement h to zero while adaptively compensating for uncertainties and external disturbances in the system model. In the next section, we show through the theoretical analysis that, under the perturbation of system uncertainties, convergence of state tracking error can be guaranteed. An aeroelastic state space representation, as expressed in (7) above, requires angle β against the trailing edge, as control input for suppressing wing section flutter. Let be the controlled state vector. The tracking error e(t) ∈ R² for the aeroelastic system can be defined as e≜x − x_d. In this study, x_d ∈ R⁴ is the desired state vector. Given that the control objective is to suppress the aeroelastic vibrations, x_d will be zero for all time periods.

3. Control Design and Convergence Analysis

The equation of motion can be expressed as

(10)

where i denotes the number of iterations; x≜x(t) ∈ R^n×1 is a vector of system states; g_i≜g(e_i, t) ∈ R^n×1 is a continuous vector function such that g(0, t) = 0, where e_i≜x_i − x_d is the state tracking error; B_i≜B(x_i, t) ∈ R^n×m is known control input distribution matrix; d_i≜d_i(x_i, t) ∈ R^m×1 is nonparametric uncertainty; θ_iξ is the parametric uncertainty function, where θ_i≜θ(x_i, t) ∈ R^m×l is a known state-dependent matrix function and ξ ∈ R^l×1 is a vector of unknown constants; u_i≜u_i(t) ∈ R^m×1 corresponds to the control input signal; and t ∈ [0, T], where T > 0 is the operation time in each iteration.

Remark 1. For the two-dimensional wing section with structural stiffness nonlinearity, parametric uncertainty was modeled in the third- and fifth-order stiffness coefficients of the pitch spring. Hence, in this work ξ is parametric uncertainty. In contrast, in [24], θ is parametric uncertainty.

Assumption 2. The nonparametric uncertainty d_i≜d_i(x_i, t) is locally Lipschitz continuous in x; that is,

(11)

where d_r≜d(x_d, t) and φ(x_i, x_d, t) are known bounding functions and ‖x‖ is a Euclidean norm for vector x ∈ Rⁿ.

Assumption 3. There exists a Barrier Lyapunov Function (BLF) V and a nonnegative class-K function γ, such that, for a vector σ ∈ Rⁿ, V → ∞ as ‖σ‖ → k_b, and

(12)

The state tracking error at the ith iteration is defined as e_i = x_i − x_d≜e_i(t). Notice that, under alignment condition, x_i(0) = x_i−1(T), we have

(13)

In order to achieve state tracking error convergence, the control law with ILC scheme in each iteration is proposed as

(14)

(15)

(16)

where p, q are positive ILC gains, φ_i≜φ(x_i, x_d, t), a_i≜∂V^T/∂e_iB_i ∈ R^1×m, and Ρ_ξ, Ρ_d represent projection operation such that

(17)

where sgn is the sign function defined as

(18)

Assumption 4. The projection bound satisfies the following condition: , and , x = 1, …, l; j = 1, …, m.

We introduce a nonnegative Barrier Composite Energy Function (BCEF) to facilitate the analysis

(19)

(20)

(21)

and

is any BLF satisfying Assumption 2.

Remark 5. In this work, we adapt a BLF in [24] as

(22)

which is also positive and will approach to infinity as ‖e‖ → k_b, where k_b is the predefined bound. From analysis that will be presented later, by BCEF, and keeping it bounded in close loop, we will guarantee convergence of state tracking error.

Theorem 6. For system (10) under alignment condition and control law proposed as (14) and two ILC laws as (15) and (16), the uniform convergence of the state tracking error e_i is guaranteed over [0, T], as iteration index i → ∞.

Proof. Consider the difference of BCEF (19) between two consecutive iterations at time t = T:

(23)

we have

(24)

Notice that, in the case of a_i = 0, we have

(25)

When a_i ≠ 0, owing to the relationships I = (1 − ε)I + εI and

, the following can be obtained:

(26)

Therefore, for the second term of (24), substituting the control law (14) into the integrand

(27)

we obtain

(28)

For

and

, applying the property (c − a) ^T(c − a)−(c − b) ^T(c − b) = (a − b) ^T(a + b − 2c) for vectors a, b, c with the same dimension, and

, as well as

, we have

(29)

(30)

where

cancels in (30) and (27).

Hence, combining all terms from (27)–(30) yields

(31)

Since a_i(d_i − d_r) ≤ ‖a_i‖‖d_i − d_r‖ ≤ ‖a_i‖φ_i‖e_i‖, therefore,

(32)

which indicates that the BCEF defined at t = T is monotonically decreasing over iteration domain.

To prove the finiteness of the time derivative of BCEF for any iteration, for any iteration index i, we have

(33)

Similar to (28), for

we have

(34)

where we substitute updating law (15) and (16) with i = 1.

For and , we have

(35)

hence

(36)

and since ξ and d_r are finite with respect to finite t and x_d, (36) indicates that E₁(t) is finite.

For any iterations i > 2, we have

(37)

Notice that, similar to (28), we can derive

(38)

For

and

, we have

(39)

Notice

is a finite term and denote its trace by D₁, and

is also a finite term. Hence we get

(40)

Since in (38)

(41)

therefore, we can obtain

(42)

The initial value of BCEF at ith iteration

. Since e_i(0) = e_i−1(T), and e_i−1(T) can be proved to be bounded by showing that BCEF is bounded in the (i − 1)th iteration. The boundedness of

and E_i(0) implies the boundedness of E_i(t), which guarantees that the boundedness of

will be guaranteed; therefore, ‖e_i(t)‖ < k_b will be ensured for any time in all iterations.

From (42), we have

(43)

Since E_i(T) is positive and E₁(T) is bounded,

converges, as i → ∞; namely,

(44)

Therefore, we can conclude that state tracking error e_i converges to zero uniformly; that is,

(45)

4. Simulation Results

This section describes the numerical simulations performed to validate the above control law design. The model parameters taken from [17] are collected in Table 1.

Table 1. System parameters.

Parameter	Value
a	−0.6719
c_h	27.43 kg/s
m_t	15.57 kg
	6.757
b	1.905 m
c_α	0.0360 N⋅s
I_cgw	0.04342 kg⋅m²
	−0.6719
x_α	r_cg/b
I_cam	0.04697 kg⋅m²
ρ	1.225 kg/m³
k_h	2844.4 N/m
	0
r_cg	−b(0.998 + a) m
m_wing	4.340 kg
	3.774
s_p	0.5945 m
m_w	5.23 kg
I_α	kg⋅m²

The velocity distributions of w_G(τ) for simulation are assumed to be (1) a triangular gust, (2) a sinusoidal gust, and (3) a graded gust. For the triangular disturbance input, one has

(46)

where H(·) denotes the unit step function, τ_G = Ut_G/b, t_G = 0.5 s, and w₀ = 0.7. The sinusoidal and graded velocity distributions are

(47)

where τ_G = Ut_G/b, t_G = 1, and w₀ = 0.07.

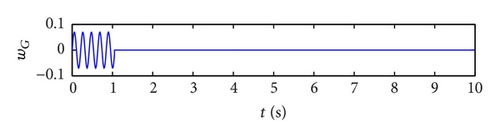
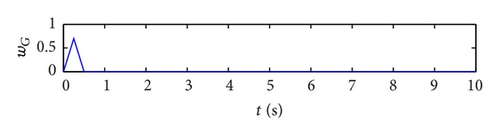
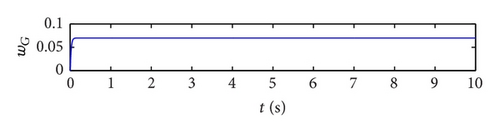
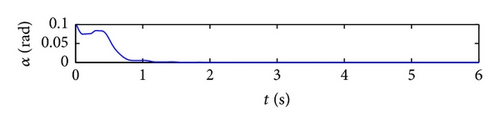
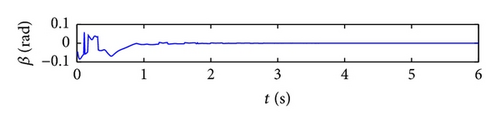
In this example, the desired trajectory variable x_d is simply selected as zero. The initial conditions for pitch angle α(t) and plunge displacement h(t) are set to be α(0) = 0.1 rad and h(0) = 0.02 m, respectively. All other state variables are also selected as zero. Here the nominal values of the unknown are given as . The upper bounds for the uncertain parameter ξ are arbitrarily selected as . The design parameters are given as follows: k_b = 0.35, p = 10, q = 5, φ = 0.2, and λ = 0.012. The poles of the linearized uncontrolled system without external disturbance for U = 10 m/s and a = −0.6719 are (−1.47 ± 14.5961i, −0.6486 ± 7.0503i). For U = 16 m/s and a = −0.6719, the poles of the linearized system are (−3.4134 ± 13.1488i, 0.8922 ± 12.2005i). Therefore, the open-loop system is stable for U = 10 m/s and unstable for U = 16 m/s. The selected velocity distributions (w_G(τ)) for (a) sinusoidal gust, (b) triangular gust, and (c) graded gust are shown in Figure 2. The sinusoidal and triangular gusts have finite duration. The open-loop responses for the velocity distributions of Figure 2 are shown in Figure 3. For triangular w_G(τ), Figures 3(a) and 3(b) indicate that the pitch angle and plunge displacement converge to zero for U = 10 m/s. However, for U = 16 m/s, the system exhibits LCOs after initial transience in all cases (Figures 3(c)–3(f)). Apparently, these undesirable oscillations in the plunge and pitch motion must be suppressed.

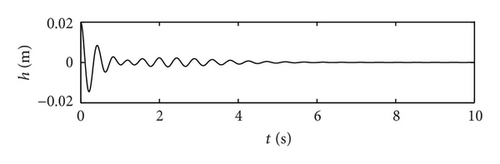
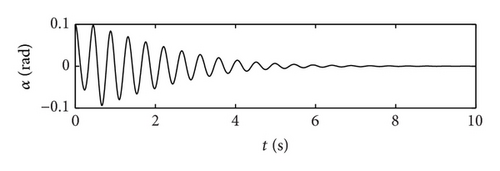
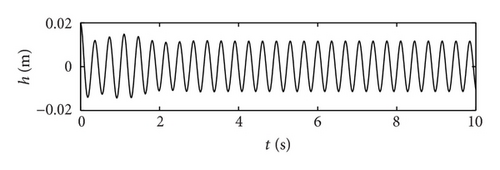
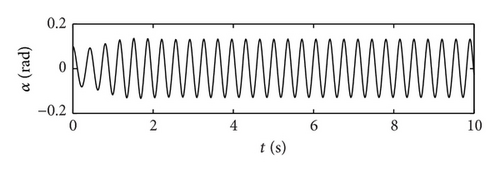
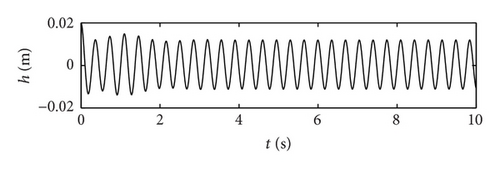
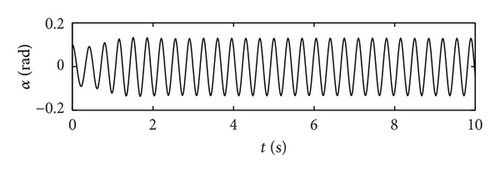
First, the responses of the closed-loop system, in the presence of a triangular gust load with intensity w₀ = 0.7 and 2.0 are obtained. For a realistic simulation, control surface deflections are limited to ±0.26 rad. Figure 4 demonstrates the response of the closed-loop system to triangular gust disturbance when w₀ = 0.7 and U = 10 m/s. With the addition of control, the pitch angle and plunge displacement converge to zero. The response time for the closed-loop is of an order less than 3 s. Compared with the open-loop response in Figures 3(a) and 3(b), the closed-loop system has a shorter convergent time. Thus, the closed-loop system responds quickly after control is implemented. Figure 5 shows the response time histories of the closed-loop system with triangular gust of larger intensity w₀ = 2 and U = 16 m/s. Evidently, in spite of the stronger gust, the pitch angle and plunge displacement converge to zero in 2 s. This result indicates that the gain of the control input increases with the velocity of the free-stream velocity; that is, the efficiency of the control surface increases at this time.

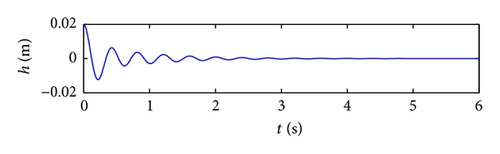
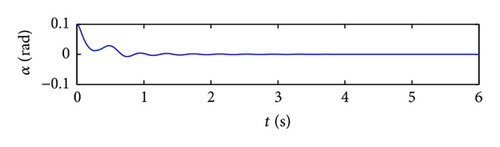
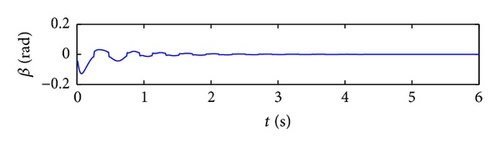
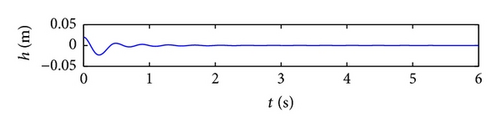
The closed-loop system perturbed by a sinusoidal disturbance input (shown in Figure 6) is simulated. The oscillations in the pitch and plunge directions are suppressed within 2 and 3 s, respectively. Figure 7 shows the response time histories of the closed-loop system under graded gust of the intensity w₀ = 0.07 and U = 16 m/s. Again the oscillations in the system are suppressed. The convergence time for the pitch angle and plunge trajectories is within 3 s. When the value of w₀ increases to 1 while the other parameters of graded gust disturbance remain unchanged, system response remains convergent to a stable state instead of to zero, as shown in Figure 8. The equilibrium values of the stable response convergences in the pitch and plunge directions are approximately 0.065 rad and −0.008 m, respectively.

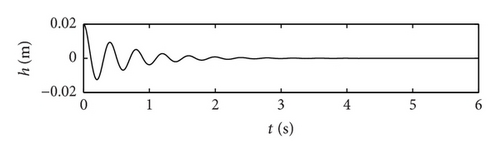
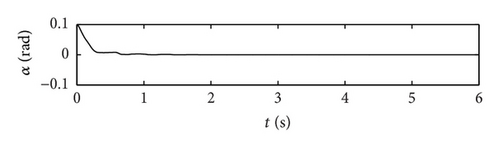
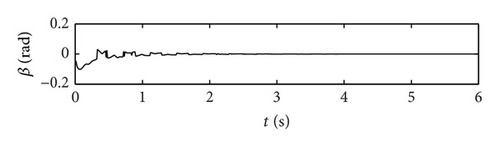
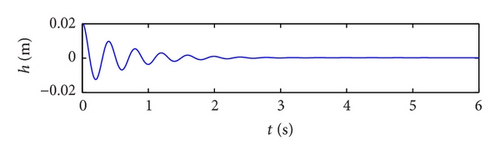
Extensive simulation has been performed for various kinds of wind gust. These results reveal that the control strategy proposed effectively suppresses the oscillation of the plunging displacement and the pitch angle, in spite of the uncertainties in the parameters and wind gusts of different shapes.

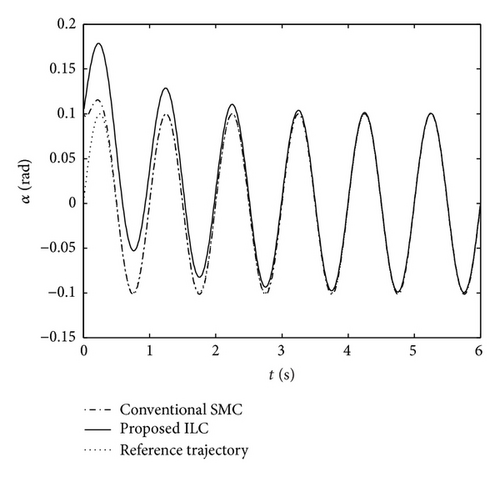
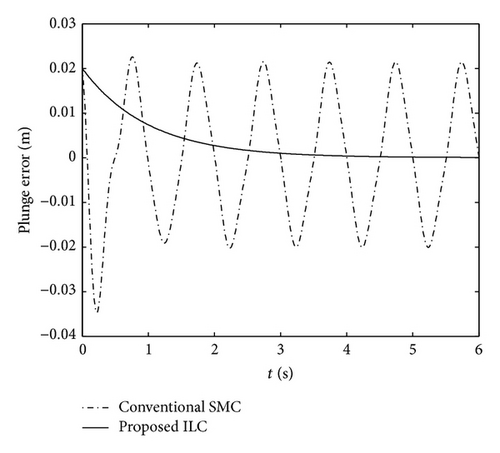
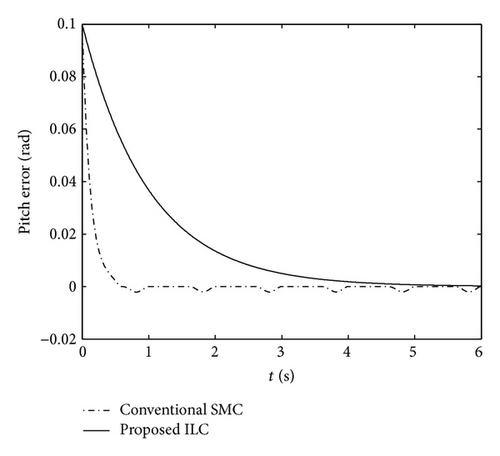
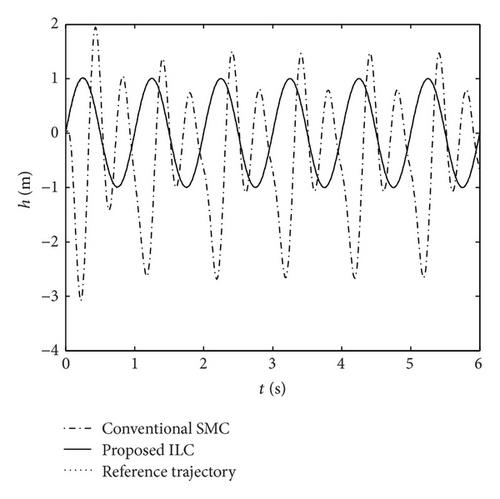
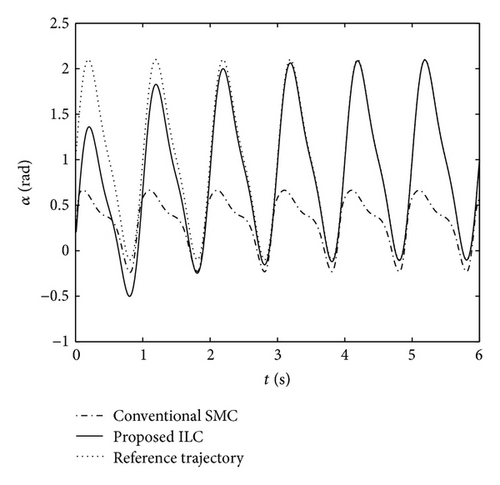
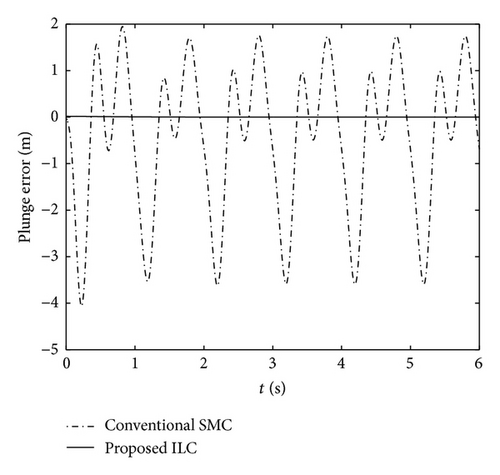
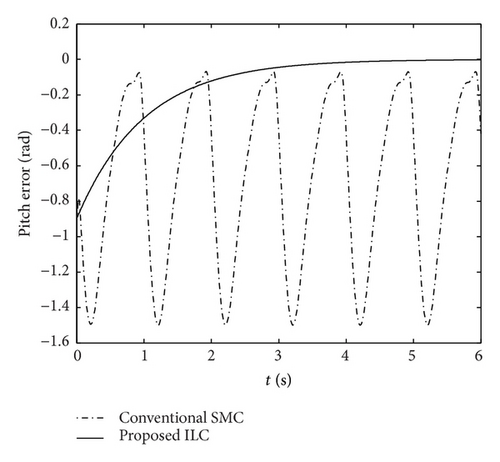
Next, for a reference tracking signal, the plunge displacement and pitch angle trajectories are x_h,d = 0.02sin⁡(2πt) and x_α,d = 0.1sin⁡(2πt), respectively. Figures 9 and 10 depicted the corresponding tracking responses. From the results shown in Figure 9, it can be observed that the conventional SMC is much faster than the proposed ILC in tracking the desired pitch trajectory, whereas it is incapable of tracking the plunge displacement trajectory. By contrast, it can be observed from Figures 9 and 10 that the desired tracking objective can be achieved when using the proposed ILC. To further evaluate the tracking performance of the proposed method, the desired tracking signals are set to be x_h,d = sin⁡(2πt) and x_α,d = 1 + sin⁡(2πt) + 0.25sin⁡(4πt), respectively. In Figures 10 and 11, it is observed that the response curves using conventional SMC have been unable to track the reference signals. However, for more complex reference signals shown in Figure 12, the proposed approach is still effective. From the analysis results, it was also found that the proposed method possesses a remarkably better tracking performance than that using conventional SMC.

5. Conclusions

In this paper, a ILC controller was proposed to suppress aeroelastic vibrations for a nonlinear wing section in the presence of parametric uncertainties and gust load. The control strategy was implemented via a single trailing-edge β control surface. The proposed scheme was developed based on alignment condition. Both parametric and nonparametric uncertainties can be effectively handled. A Barrier Composite Energy Function (BCEF) method with a novel Barrier Lyapunov Function has been used to guarantee the uniform convergence result for state tracking error. Simulation results for various gust loads were obtained. The controller accomplished suppression of the plunge displacement and pitch angle trajectory oscillations, despite uncertainties in the model parameters and triangular, sinusoidal, and graded gust loads. Unlike the traditional SMC, the proposed method has good tracking performance.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

The financial support of this research by National Natural Science Foundation of China, under Grant no. 61374032, is greatly appreciated.

References

1 Cox D. and CurtissH. C.Jr., A Modern Course in Aeroelasticity, 2004, 4th edition, Sijthoff and Noordhoff, Alphen aan den Rijn, The Netherlands.
Google Scholar
2 Lee B. H. K., Price S. J., and Wong Y. S., Nonlinear aeroelastic analysis of airfoils: bifurcation and chaos, Progress in Aerospace Sciences. (1999) 35, no. 3, 205–334, https://doi.org/10.1016/s0376-0421(98)00015-3, 2-s2.0-0033115309.
10.1016/S0376-0421(98)00015-3
Web of Science® Google Scholar
3 Dowell E., Edwards J., and Strganac T., Nonlinear aeroelasticity, Journal of Aircraft. (2003) 40, no. 5, 857–874, https://doi.org/10.2514/2.6876, 2-s2.0-0242336478.
10.2514/2.6876
Web of Science® Google Scholar
4 Fung Y., An Introduction to the Theory of Aeroelasticity, 1955, Courier Corporation, MR0071230.
Google Scholar
5 Zhao L. C. and Yang Z. C., Chaotic motions of an airfoil with non-linear stiffness in incompressible flow, Journal of Sound and Vibration. (1990) 138, no. 2, 245–254, https://doi.org/10.1016/0022-460x(90)90541-7, MR1050860, 2-s2.0-0025415998.
10.1016/0022-460X(90)90541-7
Web of Science® Google Scholar
6 Tang D. and Dowell E. H., Aeroelastic airfoil with free play at angle of attack with gust excitation, AIAA Journal. (2010) 48, no. 2, 427–442, https://doi.org/10.2514/1.44538, 2-s2.0-76949096758.
10.2514/1.44538
Web of Science® Google Scholar
7 Conner M. D., Tang D. M., Dowell E. H., and Virgin L. N., Nonlinear behavior of a typical airfoil section with control surface freeplay: a numerical and experimental study, Journal of Fluids and Structures. (1997) 11, no. 1, 89–109, https://doi.org/10.1006/jfls.1996.0068, 2-s2.0-0002203305.
10.1006/jfls.1996.0068
Web of Science® Google Scholar
8 Ko J., Strganac T. W., and Kurdila A. J., Stability and control of a structurally nonlinear aeroelastic system, Journal of Guidance, Control, and Dynamics. (1998) 21, no. 5, 718–725, https://doi.org/10.2514/2.4317, 2-s2.0-0032166295.
10.2514/2.4317
Web of Science® Google Scholar
9 Block J. J. and Strganac T. W., Applied active control for a nonlinear aeroelastic structure, Journal of Guidance, Control, and Dynamics. (1998) 21, no. 6, 838–845, https://doi.org/10.2514/2.4346, 2-s2.0-0032208512.
10.2514/2.4346
Web of Science® Google Scholar
10 Bhoir N. and Singh S. N., Output feedback nonlinear control of an aeroelastic system with unsteady aerodynamics, Aerospace Science and Technology. (2004) 8, no. 3, 195–205, https://doi.org/10.1016/j.ast.2003.10.009, 2-s2.0-1842425481.
10.1016/j.ast.2003.10.009
Web of Science® Google Scholar
11 Lee K. W. and Singh S. N., Control of a wing section using leading-and trailing-edge flaps by L1 adaptive feedback despite disturbances, Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, January 2013, Dallas, Tex, USA, AIAA Paper 2013-0333, 2-s2.0-84881426248.
Google Scholar
12 Singh S. N. and Yim W., State feedback control of an aeroelastic system with structural nonlinearity, Aerospace Science and Technology. (2003) 7, no. 1, 23–31, https://doi.org/10.1016/s1270-9638(02)00004-4, 2-s2.0-0038066373.
10.1016/S1270-9638(02)00004-4
Web of Science® Google Scholar
13 Li D., Guo S., and Xiang J., Aeroelastic dynamic response and control of an airfoil section with control surface nonlinearities, Journal of Sound and Vibration. (2010) 329, no. 22, 4756–4771, https://doi.org/10.1016/j.jsv.2010.06.006, 2-s2.0-77955429848.
10.1016/j.jsv.2010.06.006
Web of Science® Google Scholar
14 Pettit C. L., Uncertainty quantification in aeroelasticity: recent results and research challenges, Journal of Aircraft. (2004) 41, no. 5, 1217–1229, https://doi.org/10.2514/1.3961, 2-s2.0-7544220667.
10.2514/1.3961
Web of Science® Google Scholar
15 Beran P. S., Pettit C. L., and Millman D. R., Uncertainty quantification of limit-cycle oscillations, Journal of Computational Physics. (2006) 217, no. 1, 217–247, https://doi.org/10.1016/j.jcp.2006.03.038, 2-s2.0-33746672013.
10.1016/j.jcp.2006.03.038
Web of Science® Google Scholar
16 Ko J., Strganac T. W., and Kurdila A. J., Adaptive feedback linearization for the control of a typical wing section with structural nonlinearity, Nonlinear Dynamics. (1999) 18, no. 3, 289–301, https://doi.org/10.1023/a:1008323629064, 2-s2.0-0032647992.
10.1023/A:1008323629064
Web of Science® Google Scholar
17 Strganac T. W., Ko J., and Thompson D. E., Identification and control of limit cycle oscillations in aeroelastic systems, Journal of Guidance, Control, and Dynamics. (2000) 23, no. 6, 1127–1133, https://doi.org/10.2514/2.4664, 2-s2.0-0034316194.
10.2514/2.4664
Web of Science® Google Scholar
18 Defoort M., Floquet T., Kokosy A., and Perruquetti W., A novel higher order sliding mode control scheme, Systems & Control Letters. (2009) 58, no. 2, 102–108, https://doi.org/10.1016/j.sysconle.2008.09.004, 2-s2.0-58149175803.
10.1016/j.sysconle.2008.09.004
Web of Science® Google Scholar
19 Gujjula S., Singh S. N., and Yim W., Adaptive and neural control of a wing section using leading- and trailing-edge surfaces, Aerospace Science and Technology. (2005) 9, no. 2, 161–171, https://doi.org/10.1016/j.ast.2004.10.003, ZBL1195.74119, 2-s2.0-14544302116.
10.1016/j.ast.2004.10.003
Web of Science® Google Scholar
20 Behal A., Marzocca P., Rao V. M., and Gnann A., Nonlinear adaptive control of an aeroelastic two-dimensional lifting surface, Journal of Guidance, Control, and Dynamics. (2006) 29, no. 2, 382–390, https://doi.org/10.2514/1.14011, 2-s2.0-33645575966.
10.2514/1.14011
Web of Science® Google Scholar
21 Marsden C. C. and Price S. J., Transient and limit cycle simulation of a nonlinear aeroelastic system, Journal of Aircraft. (2007) 44, no. 1, 60–70, https://doi.org/10.2514/1.21367, 2-s2.0-33847734062.
10.2514/1.21367
Web of Science® Google Scholar
22 Li D., Xiang J., and Guo S., Adaptive control of a nonlinear aeroelastic system, Aerospace Science and Technology. (2011) 15, no. 5, 343–352, https://doi.org/10.1016/j.ast.2010.08.006, 2-s2.0-79959963373.
10.1016/j.ast.2010.08.006
Web of Science® Google Scholar
23 Xu J.-X. and Jin X., State-constrained iterative learning control for a class of MIMO systems, IEEE Transactions on Automatic Control. (2013) 58, no. 5, 1322–1327, https://doi.org/10.1109/tac.2012.2223353, 2-s2.0-84891811555.
10.1109/TAC.2012.2223353
Web of Science® Google Scholar
24 Sampson P., Freeman C., Coote S., Demain S., Feys P., Meadmore K., and Hughes A., Using functional electrical stimulation mediated by iterative learning control and robotics to improve arm movement for people with Multiple Sclerosis, IEEE Transactions on Neural Systems and Rehabilitation Engineering. (2015) no. 99, 1, https://doi.org/10.1109/TNSRE.2015.2413906.
10.1109/TNSRE.2015.2413906
PubMed Web of Science® Google Scholar
25 Chen Y. Q., Moore K. L., Yu J., and Zhang T., Iterative learning control and repetitive control in hard disk drive industry—a tutorial, Proceedings of the 45th IEEE Conference on Decision and Control (CDC ′06), December 2006, San Diego, Calif, USA, IEEE, 2338–2351, https://doi.org/10.1109/CDC.2006.377581, 2-s2.0-39649093659.
10.1109/CDC.2006.377581
Google Scholar
26 Zhao Y. M., Lin Y., Xi F., and Guo S., Calibration-based iterative learning control for path tracking of industrial robots, IEEE Transactions on Industrial Electronics. (2015) 62, no. 5, 2921–2929, https://doi.org/10.1109/tie.2014.2364800.
10.1109/TIE.2014.2364800
Web of Science® Google Scholar
27 Basler S., Dunow P., Marquardt M., and Daasch A., Application of iterative learning control methods for a service robot with multi-body kinematics, Proceedings of the 20th IEEE International Conference on Methods and Models in Automation and Robotics (MMAR ′15), August 2015, Miedzyzdroje, Poland, 465–470, https://doi.org/10.1109/MMAR.2015.7283920.
10.1109/MMAR.2015.7283920
Google Scholar
28 Kapania N. R. and Gerdes J. C., Path tracking of highly dynamic autonomous vehicle trajectories via iterative learning control, Proceedings of the American Control Conference (ACC ′15), July 2015, Chicago, Ill, USA, IEEE, 2753–2758, https://doi.org/10.1109/acc.2015.7171151.
10.1109/acc.2015.7171151
Google Scholar
29 Marzocca P., Librescu L., and Chiocchia G., Aeroelastic response of 2-D lifting surfaces to gust and arbitrary explosive loading signatures, International Journal of Impact Engineering. (2001) 25, no. 1, 41–65, https://doi.org/10.1016/S0734-743X(00)00033-6, 2-s2.0-0035218131.
10.1016/S0734-743X(00)00033-6
Web of Science® Google Scholar

Citing Literature

All articles

Iterative Learning Control of a Nonlinear Aeroelastic System despite Gust Load

Abstract

1. Introduction

2. Aeroelastic Model and Control Problem

3. Control Design and Convergence Analysis

4. Simulation Results

5. Conclusions

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Iterative Learning Control of a Nonlinear Aeroelastic System despite Gust Load

Abstract

1. Introduction

2. Aeroelastic Model and Control Problem

3. Control Design and Convergence Analysis

4. Simulation Results

5. Conclusions

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Related

Information