The performance index of a suspension system is a function of the maximum and minimum values over the parameter interval. Thus metamodel-based techniques can be used for designing suspension system hardpoints locations. In this study, an adaptive metamodel-based optimization approach is used to find the proper locations of the hardpoints, with the objectives considering the kinematic performance of the suspension. The adaptive optimization method helps to find the optimum locations of the hardpoints efficiently as it may be unachievable through manually adjusting. For each iteration in the process of adaptive optimization, prediction uncertainty is considered and the multiobjective optimization method is applied to optimize all the performance indexes simultaneously. It is shown that the proposed optimization method is effective while being applied in the kinematic performance optimization of a McPherson suspension system.

1. Introduction

The suspension K&C characteristics have directly effects on vehicle handling and riding performances and thus gain much effort and are of great importance in vehicle development. With bush uncertainty and mechanical flexibility, it is very difficult to predict sensitivity of hardpoints locations in the kinematic performance of a suspension system as they are highly nonlinear and coupled [1, 2]. Traditional chassis developing, which benefits from the development of modern virtual prototyping technology, can now do system design effectively through some techniques, like the DOE (design of experiment) technique, as well as other experience-based attempts [3–5]. However, the mechanism of the suspension system is designed by trial and error based on the designer’s experiences and intuition, which will be time-consuming in finding a sufficiently good solution since a lot of attempts may be needed in doing virtual prototyping simulations. A featured optimization technique may be useful to give guidance through the design process.

The performance index of a suspension system is a function of the maximum and minimum values over the parameter interval [6, 7]. Thus, it is impossible to apply directly a well-developed optimization algorithm based on gradient information. It can be very difficult to evaluate the analytical design sensitivity of the hardpoints locations because the deviation is defined by using the maximum and minimum values over the parameter interval. Metamodeling techniques, which were initially developed as “surrogates” of the expensive simulation process for improving the overall computation efficiency and quality [8], are useful in such a field. Metamodel-based methods in vehicle design area mainly focused on FEM related problems [9]. Much work has been done in suspension design area, most of which focused on complex structural related area. The authors in [10] studied a mechanical analysis of a suspension optimal design for suspension system based on reliability analyses, taking into consideration tolerances and grafting a reliability analysis that applied the mean-value first order method with tolerance optimization. Choi et al. recently studied optimal design for automotive suspension systems based on reliability analyses for enhancing kinematics and compliance characteristics; they performed reliability optimization with the single-loop single-variable method by using the results from a deterministic optimization as initial values. The robust design problem was solved with 1700 analyses for 15 design variables and four random constants [11]. Recently, researches on applying metamodel-based optimization techniques to the K&C performance design of vehicle suspension systems were tried and gained reasonable good results. Kang et al. introduced a robust suspension system design approach, which takes into account the kinematic behaviors influenced by bush compliance uncertainty, using a sequential approximation optimization technique. The robust design problem has 18 design variables and 18 random constants with uncertainty [12]. After then, the team proposed a so-called target cascading method for the robust design optimization process of suspension system for improving vehicle dynamic performances [13]. The design target of the system is cascaded from a vehicle level to a suspension system level. The design problem structure of suspension system is defined as a hierarchical multilevel design optimization, and the design problem for each level is solved using the robust design optimization technique based on a metamodel. The researches above opened the way for doing suspension system optimization by using metamodel-based techniques with their effectiveness tested, which motivated us to further research along the direction. However, the former research neither considered optimizing several objectives simultaneously to make them stable in comparable intervals, nor gave the searching guidance for each design parameter in accelerating the convergence of objective parameters.

In this paper, we employ a new adaptive metamodel-based optimization approach for guiding suspension system design in determining appropriate hardpoints locations. The following characteristics distinguish the approach from other metamodel-based applications in suspension system design. (1) As we have several vehicle performance related parameters to be optimized, adaptive weighting factors are used for multiobjective optimization to ensure that all the objectives are optimized simultaneously. (2) For each iteration of the adaptive optimization, both predicted mean value and prediction standard deviation are considered in case of the system converging to the wrong optimum values. (3) We select kriging method as it is more accurate and efficient than other metamodeling methods in solving highly nonlinear problems. (4) The optimization approach provides the possible trends in selecting hardpoints locations for optimizing the system performances. We organize the paper in the following manner. Section 2 introduces the engineering requirements for the optimization problem in suspension system design. Section 3 presents the methodology of adaptive metamodel-based optimization considering modeling uncertainty. The application of adaptive optimization method in suspension system is given in Section 4. Section 5 compares the results of proposed adaptive metamodel-based optimization considering modeling uncertainty and the regular adaptive metamodeling approach. At last, Section 6 summarizes the contents of this research.

2. Optimization Problem in Suspension System

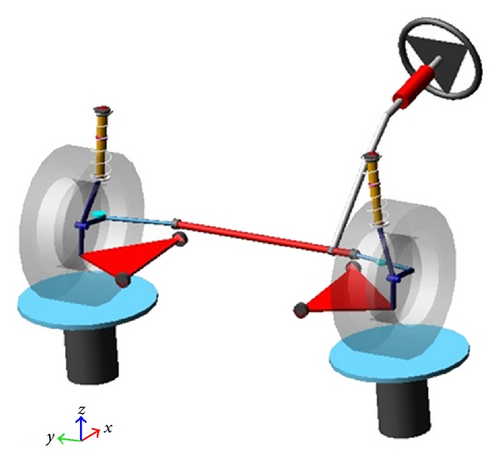
In multibody dynamics point of view, a suspension system can be classified into several groups according to the mechanical joints. In this study, we take McPherson type suspension system in consideration, which is sensitive to the kinematic performance. Figure 1 shows a kinematic structure model of a McPherson suspension system. Major components include the strut, the lower control arm, the tie rod, and the knuckle. Connections between individual components are spherical, revolute, and universal joints, as well as compliance elements such as springs, dampers, and bushings. The design purpose of this study is to determine the locations of the hardpoints according to the system kinematic performances, without considering the elastic deformations of the rigid components except for compliance elements. The commercial software ADAMS, which can easily get the suspension system performance, is employed for modeling and analyzing the suspension system.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The kinematic structural model of a McPherson suspension system.

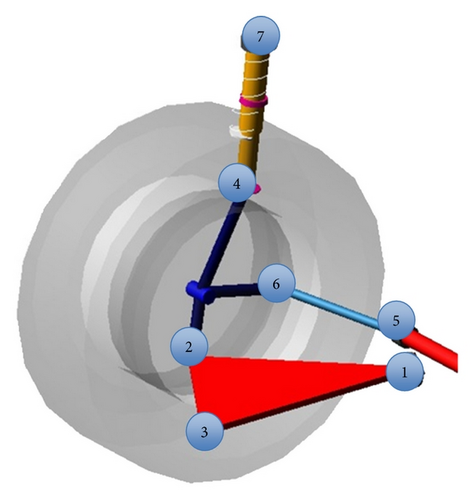
The kinematic characteristics of the system include the positions of the fixed points of the suspension system. To achieve optimal solution for suspension system, designing a good kinematic performance is the first step and we thus carry out kinematic optimization of the suspension system in this study. For that purpose, the chosen suspension performance indexes are the deviations in the camber angle, the caster angle, the kingpin incline angle, and the toe angle during the wheel stroke. Camber angle is the angle between the vertical axis of the wheels used for steering and the vertical axis of the vehicle when viewed from the front or rear. It is defined as positive when the top of the wheel moves to the outside. The camber angle alters the handling qualities of a suspension system; in particular, a negative camber angle improves grip when cornering. Caster angle is the angular displacement from the vertical axis of the suspension of a steered wheel in a vehicle, measured in the longitudinal direction. It is the angle between the pivot line (in a car, an imaginary line that runs through the center of the upper ball joint to the center of the lower ball joint) and vertical line. On most modern designs, the kingpin is set at an angle relative to the true vertical line, which is the kingpin inclination angle, as viewed from the front or back of the vehicle. The angle has an important effect on the steering, making it tend to return to the straight ahead or center position. Toe angle is the symmetric angle that each wheel makes with the longitudinal axis of the vehicle, as a function of static geometry and kinematic and compliant effects. The toe angle change plays an important role in determining the apparent transient oversteer or understeer. Positive toe is the front of the wheel pointing in towards the centerline of the vehicle. Negative toe is the front of the wheel pointing away from the centerline of the vehicle. Large errors will have a negative effect on the behavior of the chassis when braking or accelerating.

In suspension system design, the locations of hardpoints are the most important influencing factors that determine the system kinematic performances. Although engineers obtained some experiences on adjusting the locations of the hardpoints, much effort is still needed on trying different trials. Furthermore, all the geometric parameters of suspension system are coupled, which make finding the influence of the hardpoints locations on the system performances a more tough work, not mentioning there are several objectives to be determined. In this study, while determining the locations of the key hardpoints, we select the important characteristics, that is, the variations of the camber angle, the caster angle, the kingpin incline angle and the toe angle, for the objectives since they are related much to the kinematic performance. An adaptive metamodel-based optimization approach will be proposed in the next section considering modeling uncertainties.

3. Adaptive Metamodel-Based Optimization Method

3.1. Metamodeling Method

In metamodeling, the relationship between a vector of input parameters, x, and an output parameter, Y, can be formulated as

(1)

where Y is a random output variable,

is the approximated relationship, and ε is the error of metamodel due to the uncertainty introduced by the metamodeling method. Many different metamodels, such as multivariate polynomial, radial basis function (RBF), and kriging, can be used to build the approximation relationship

. In metamodeling, first m sample data (x_i, y_i) (i = 1,2, …, m) are collected to build

. When an input point x₀ is given, the metamodel can then be used to predict the output Y₀ using

(2)

Among various metamodeling schemes, kriging method is often selected due to its high accuracy and efficiency for solving nonlinear problems [14]. Kriging method was originated from the geostatistics community [15] and used by Sacks et al. [16] for modeling computer experiments. Kriging method is based on the assumption that the true system response, Y, can be modeled by

(3)

where f_i(·) is a regression function, β_i is the coefficient for f_i(·), m + 1 is the number of regression functions, and Z(·) is the stochastic process with zero mean and covariance defined by

(4)

where σ² is the process variance, R_jk(·) is the correlation function, and θ is a vector with coefficients to be determined.

For ordinary kriging, the linear part of (3) is usually assumed to be a constant, whereas the correlation function R_jk(θ, x_j, x_k) is generally formulated as

(5)

where p is the dimension of x, x_ji is the ith component of x_j, x_ki is the ith component of x_k, and Q(·) is usually assumed to be Gaussian as

(6)

The linear predictor of kriging method can be formulated as

(7)

where c^T(·) is the coefficient vector and y is the vector of the observations at the sample sites (x₁, …, x_n)

(8)

Through minimizing the prediction variance

(9)

concerning the coefficient vector c^T(x), the best linear unbiased predictor (BLUP) is solved as [17]

(10)

where

(11)

The coefficients in θ can be obtained by using maximum likelihood estimation as [17]

(12)

where |R| is the determinant of R and σ is obtained by generalized least squares fit as [17]

(13)

where β^* is the vector with coefficients achieved from generalized least squares fit and is calculated by

(14)

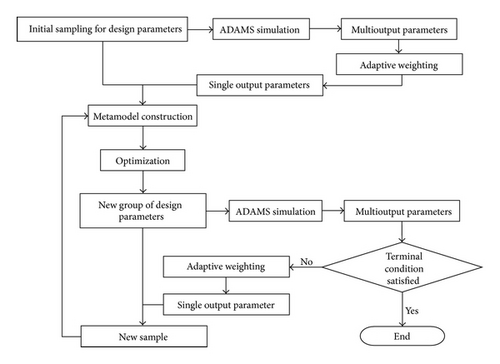
When metamodeling is used for solving specific problems, collection of sample data in specific parameter space, rather than the whole parameter space, is then required to improve the quality and efficiency. This issue is critical when expensive or extensive experiments/simulations are required to collect the sample data. Since the relationship is unknown at the beginning, initial samples are usually collected to build the initial metamodel. This developed metamodel is then used to identify the input parameters that have the best potential to lead to the expected output result. Due to the errors of the metamodel, the actual output obtained from experiment/simulation is usually different from the expected one. The previously obtained metamodel is subsequently updated to improve its quality using the new pair of input-output data. The method to iteratively modify the metamodel through an iterative sampling process is called adaptive metamodeling.

3.2. Adaptive Metamodel-Based Optimization

When adaptive metamodeling is used for optimization, the optimization process can be referred to as adaptive metamodel-based optimization [8]. The detailed algorithm for adaptive metamodel-based optimization is introduced here and we call it adaptive optimization in later parts of the paper. First the m initial samples with input parameters x_i (i = 1,2, …, m) and output parameter Y_i (i = 1,2, …, m) are collected to build the metamodel:

(15)

Based on the metamodel relationship f_m, we can identify the potential input parameters x^* that lead to the minimum output parameter through optimization:

(16)

The optimization result of x^* is then selected as the vector of input parameters for the (m + 1)th sample x_m+1. The output Y_m+1 corresponding to the x_m+1 is subsequently obtained through experiment or simulation. The new pair of data, (x_m+1, Y_m+1), together with all the previously collected sample data are used to update the metamodel into a new relationship f_m+1:

(17)

The process of identifying the potential optimal input parameters, obtaining the output parameter through experiment/simulation, and updating the metamodel is continued iteratively until the optimization criteria are satisfied.

3.3. Adaptive Optimization considering Modeling Uncertainty

In the process of adaptive optimization, the prediction uncertainty of the developed metamodel would influence the accuracy of the predicted optimum. Minimizing the f_m directly to find the optimal input parameters may not lead to good convergence for output parameters. The dual response surface methodology is a powerful tool for simultaneously optimizing the mean and the variance of responses to tackle the problem of misleading [18]. Lin and Tu [19] gave a dual response surface method using the mean squared error (MSE) approach as follows:

(18)

where

is the predicted response value, T is the target value, and

is the prediction standard deviation. Following the format of (18), the objective function for our adaptive optimization can be defined as follows:

(19)

We will formulate the specific problem for McPherson suspension system using the adaptive metamodel-based optimization considering prediction uncertainty in the coming section.

4. Adaptive Optimization considering Modeling Uncertainty in McPherson Suspension

To investigate the performance of the designated suspension system, a classic McPherson suspension system is modeled in ADAMS, as shown in Figure 2. The classic parallel wheel travel suspension system analysis can be employed to do system analysis. Vertical bound and rebound of 50 mm are used. By changing the locations of each hardpoint, the corresponding change of kinematic characteristics can be obtained.

In this study, we take the locations of the 7 key hardpoints labeled in Figure 1 as variables, 3 variables at each hardpoint, that is, the coordinates of the hardpoint along axes x, y and z of the vehicle coordinate. Therefore we have 21 variables (v1–v21) for the designated suspension system. Table 1 listed the 21 variables versus the hardpoint coordinate.

Table 1. The key hardpoints and corresponding variables.

Number	Hardpoint name	Coordinates	Variables
1	LCA_front	x, y, z	v1, v2, v3
2	LCA_outer	x, y, z	v4, v5, v6
3	LCA_rear	x, y, z	v7, v8, v9
4	Struct_lwr	x, y, z	v10, v11, v12
5	Tierod_inner	x, y, z	v13, v14, v15
6	Tierod_outer	x, y, z	v16, v17, v18
7	Top_mount	x, y, z	v19, v20, v21

For the kinematic characteristics, as stated in Section 2, we choose the camber angle, the caster angle, the kingpin incline angle, and the toe angle as the objective parameters to be designed and optimized. For McPherson suspension system, small variations of the four estimate angles surely are more acceptable. Thus, we choose the four optimization objectives to be the minimum deviations of the four angles versus wheel travel from rebound −50 mm to bound 50 mm.

We thus have 21 design variables as input parameters and 4 optimum objectives as output parameters. The optimization problem is clearly highly nonlinear and coupled on the input variables. We thus employ the metamodeling method for the optimal design. We clearly have several optimization objectives; the usual way that people deal with multiobjective optimization problems is assigning weighting factors to each objective and then adding them to build a single objective. However, the predefined weighting factors may not be proper for the whole process of optimization. In our work, we only assign the same value to the weighting factors for the output parameters in the initial samples. Adaptive weighting factors are used in the process of adaptive optimization, which is carried out as follows:

(20)

where r is the number of output parameters and m is number of initial samples. The m initial samples with input parameters x_i (i = 1,2, …, m) and output parameter Y_i (i = 1,2, …, m) are collected to build the metamodel and obtain the new group of input parameters using (19).

The initial metamodel is built on the data generated from Latin hypercube sampling [20], which has the following advantages: (1) its sample mean has a relatively smaller variance compared with simple random sampling, (2) it can be used for generating design points when the number of input variables is large and a great many runs are required, and (3) it is cheap in computing and easy for implementation compared with other more complex sampling methods. By using ADAMS batch processing tools, the initial sets samples can easily be obtained. With the built initial metamodel, the adaptive optimization method introduced in Section 3.3 can be used.

The 4 output parameters corresponding to the new group of input parameters are subsequently obtained through simulations. The weighting factors w_i are adjusted using (21) and the value of Y_M+1 is calculated using (22). The larger the Y_iM is, the larger weighting factor will be assigned to it in order to minimize all the output parameters at the same time. Consider

(21)

where M + 1 is the number of samples for each iteration in the process of adaptive optimization, and N is the total sample size. Consider

(22)

The new pair of data, (x_M+1, Y_M+1), together with all the previously collected sample data are used to update the metamodel into a new relationship. The optimization process is stopped when the change of the objective function in several consecutive iterations is less than a predefined value, or the maximum number of iterations is reached.

As there are 4 output parameters as optimizing objectives for our suspension system, (23) is used to transform the multiobjective optimization into single objective optimization. The adaptive weighting factors are obtained from (21). The design objective is to minimize Y as in

(23)

The flowchart for the adaptive optimization process is given in Figure 3.

5. Comparisons and Analysis of the Optimization Results

The number of the initial sample is selected as 50 to build the initial metamodel. 50 initial samples may not be enough for a metamodeling problem with 21 variables; however, due to the cost consideration in engineering design, we just initially choose 50 samples and gradually add new samples during the design process. Based on the initial metamodel, more trails are sampled sequentially and adaptively to approach the optimum value. When the total sample size reaches 100, the values of the output parameters are generally stable. We analyze each of the 4 output parameters individually every time while we update the metamodel. For this high dimensional (21D input) problem, 100 samples may not be enough to reach the optimum value. However, we can evaluate its effectiveness through its convergent trend. The optimization results are shown in Figure 4. The value of the objective function is well converged and the variations of the 4 output parameters are generally stable.

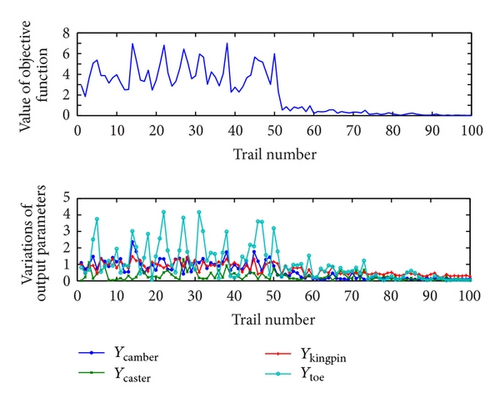
The 4 types of curves with “•”, “×”, “+”, and “o” indicate the camber angle variation, the caster angle variation, the kingpin incline angle variation, and the toe angle variation. The trail distributions from 1 to 50 are obtained from Latin hypercube sampling in the whole design space for building the initial metamodel. From Figure 4, we can see that corresponding to the same design interval (−50, 50), the variation interval for the camber angle, the caster angle, the kingpin incline angle, and the toe angle are (0, 2.5), (0, 4.5), (0, 1.5), and (0, 4.5). While adaptive optimization is applied for the trails from 51 to 100, the variation intervals decrease and the curves become smooth. The adaptive weighting factors help the output parameters with different variation intervals converge to the same variation interval (0, 0.33). It can be seen from Figure 4 that our method succeeds in optimizing the 4 output parameters simultaneously while the value of the objective function is well converged. Table 2 listed the initial and the optimized hardpoints locations for the suspension system. We have chosen the 100th sample as the optimized result.

Table 2. The initial and optimized hardpoints coordinates.

Variables	Initial	Optimized
v1, v2, v3	160, −410, 265	195.7, −381, 234
v4, v5, v6	−80, −710, 165	−95, −710.6, 213
v7, v8, v9	190, −395, 185	190.6, −366, 166
v10, v11, v12	50, −630, 530	64.6, −622, 531.3
v13, v14, v15	155, −440, 355	130, −391.2, 305
v16, v17, v18	210, −700, 240	219.5, −749, 290
v19, v20, v21	7.5, −603.8, 850	35.2, −642, 873.6

As to the regular adaptive optimization, prediction standard deviation is not considered in the process of the optimization, and the objective function is usually defined as in (16). We used the same 50 initial samples to build the initial metamodel and then apply the objective function given in (16) to search the subsequent 50 samples. We compare the mean output values of the last 5 samples for each of the 4 output parameters from optimization objective functions defined by (19) and (16), as shown in Table 3. The mean output values are compared by a ratio, α, representing how much the adaptive optimization method considering uncertainty is better than the regular adaptive optimization method. Here,

(24)

where Var _mean indicates the mean output value in the last 5 iterations from regular adaptive optimization method, and Var _mean(un) gives the mean output value in the last 5 iterations from adaptive optimization method considering the modeling uncertainty.

Table 3. Comparison between adaptive optimization considering modeling uncertainty and regular adaptive optimization.

Optimization objective function

Camber angle

variation

Caster angle

variation

Kingpin angle

variation

Toe angle

variation

Adaptive optimization considering modeling uncertainty

0.1056

0.0916

0.3044

0.0577

Regular adaptive optimization

0.1616

0.1585

0.4717

0.1045

53.03%

73.03%

54.96%

81.11%

From Table 3, we could see that the adaptive optimization method with consideration of modeling uncertainty performs better. The adaptive optimization performs better up to 81.11% for all the four output parameters. The reason should be that the number of sample points is far from sufficient to build an accurate metamodel, especially at the very beginning. Thus the optimization result based on the built metamodel only considering predicted mean value may not converge to the right direction. With the prediction standard deviation being considered at the same time, the inaccuracy of the metamodel can be compensated to some extent to approach the right direction.

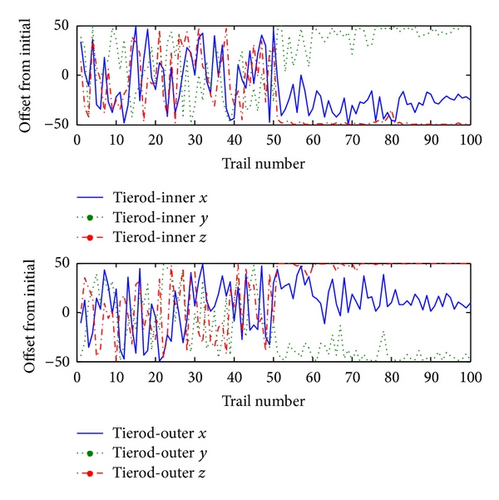
What is interesting is that the approach can illustrate a suggested trend that the hardpoints should be moved over to. Figure 5 shows the approximate trends that the hardpoints tierod inner and tierod outer stay around during the optimization procedure, and other hardpoints perform similarly. From this figure, it can be seen that the 3 coordinate values for each input parameter tend to change in a smaller interval rather than change in the original design interval (−50, 50). This result from our research can help to reduce the design space in the process of adaptive optimization, in order to greatly improve the optimization efficiency, which would be especially significant for higher dimensional problems.

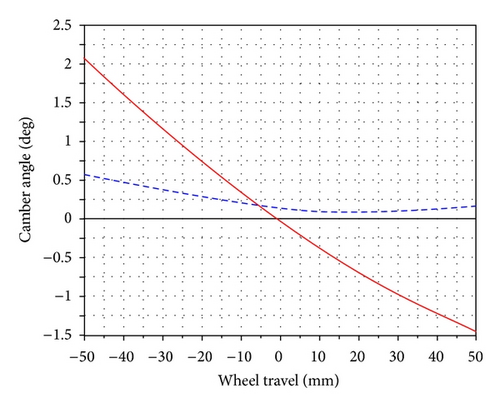
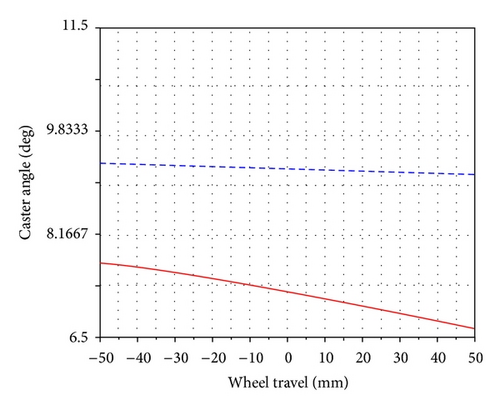
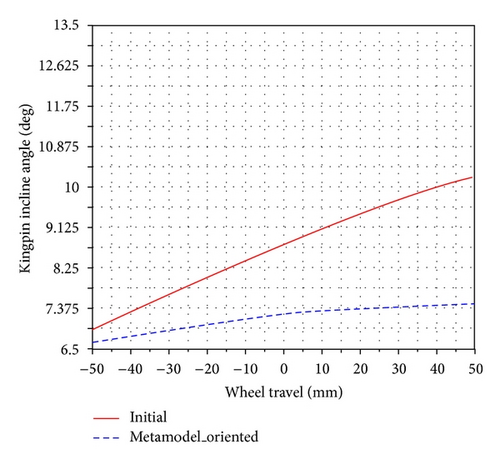
The apparent result that the optimization procedure can achieve is reducing the variation of the design objectives. Figure 6 gives the variations of the camber angle, the caster angle, the kingpin incline angle, and the toe angle, versus the wheel travel for the optimized trail number 100 and the initial trail during the parallel suspension travel analysis. We can see that the optimized data significantly reduced the variation of the camber angle, the kingpin incline angle, and the toe angle, while also slightly reducing the caster angle. This shows the effectiveness of the proposed approach on guiding to search for the optimized solution for kinematic performance design of vehicle suspension systems. Other related parameters can be considered in a similar way.

6. Conclusion

This study introduced adaptive metamodel-based optimization considering modeling uncertainty to optimize the kinematic performance of a McPherson suspension system. The optimization design problem is of 21 input parameters and 4 output parameters. The multioutput optimization in the McPherson suspension system is transformed to a single output optimization problem using adaptive weighting factors. 50 initial samples and 50 sequential trails are generated to analyze the convergent trend of the objective parameters. It shows that the proposed optimization method provided a set of relatively good results of the 4 output objective parameters simultaneously for the 50 sequential trails. Possible optimal design trends of the hardpoints are given as the trail goes on. Comparisons showed that the adaptive metamodel-based optimization method considering modeling uncertainty worked better than general adaptive metamodel-based optimization for the suspension design problem.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

This work is supported by NSFC Grant no. 11302074.

References

1 Blundell M. and Harty D., The Multibody Systems Approach to Vehicle Dynamics, 2004, Maple-Vail, Kirkwood, NY, USA.
Google Scholar
2 Zapateiro M., Pozo F., Karimi H. R., and Luo N., Semiactive control methodologies for suspension control with magnetorheological dampers, IEEE/ASME Transactions on Mechatronics. (2012) 17, no. 2, 370–380, 2-s2.0-84856339851, https://doi.org/10.1109/TMECH.2011.2107331.
10.1109/TMECH.2011.2107331
Web of Science® Google Scholar
3 Li H., Jing X., and Karimi H. R., Output-feedback-based H_∞ control for active suspension systems with control delay, IEEE Transactions on Industrial Electronics. (2013) 61, no. 1, 436–446.
10.1109/TIE.2013.2242418
Web of Science® Google Scholar
4 Zhang H., Shi Y., and Mehr A. S., Robust H_∞ PID control for multivariable networked control systems with disturbance/noise attenuation, International Journal of Robust and Nonlinear Control. (2012) 22, no. 2, 183–204, https://doi.org/10.1002/rnc.1688, MR2875191, ZBL1244.93047.
10.1002/rnc.1688
Web of Science® Google Scholar
5 Wang R., Zhang H., and Wang J., Linear parameter-varying controller design for four-wheel independently actuated electric ground vehicles with active steering systems, IEEE Transactions on Control Systems Technology. (2013) https://doi.org/10.1109/TCST.2013.2278237.
10.1109/TCST.2013.2278237
Web of Science® Google Scholar
6 Shuai Z., Zhang H., Wang J., and Li J., Combined AFS and DYC control of four-wheel-independent-drive electric vehicles over CAN network with time-varying delays, IEEE Transactions on Vehicular Technology. (2013) https://doi.org/10.1109/TVT.2013.2279843.
10.1109/TVT.2013.2279843
Google Scholar
7 Zhang H., Wang J., and Shi Y., Robust H_∞ sliding-mode control for Markovian jump systems subject to intermittent observations and partially known transition probabilities, Systems & Control Letters. (2013) 62, no. 12, 1114–1124, https://doi.org/10.1016/j.sysconle.2013.09.006, MR3130489.
10.1016/j.sysconle.2013.09.006
Web of Science® Google Scholar
8 Wang G. G. and Shan S., Review of metamodeling techniques in support of engineering design optimization, Journal of Mechanical Design, Transactions of the ASME. (2007) 129, no. 4, 370–380, 2-s2.0-34248346299, https://doi.org/10.1115/1.2429697.
10.1115/1.2429697
Web of Science® Google Scholar
9 Zhu P., Zhang Y., and Chen G.-L., Metamodel-based lightweight design of an automotive front-body structure using robust optimization, Proceedings of the Institution of Mechanical Engineers D. (2009) 223, no. 9, 1133–1147, 2-s2.0-70350351259, https://doi.org/10.1243/09544070JAUTO1045.
10.1243/09544070JAUTO1045
Web of Science® Google Scholar
10 Chun H. H., Kwon S. J., and Tak T., Reliability based design optimization of automotive suspension systems, International Journal of Automotive Technology. (2007) 8, no. 6, 713–722.
Web of Science® Google Scholar
11 Choi B.-L., Choi J.-H., and Choi D.-H., Reliability-based design optimization of an automotive suspension system for enhancing kinematic and compliance characteristics, International Journal of Automotive Technology. (2005) 6, no. 3, 235–242, 2-s2.0-33745599874.
Web of Science® Google Scholar
12 Kang D. O., Heo S. J., and Kim M. S., Robust design optimization of the McPherson suspension system with consideration of a bush compliance uncertainty, Proceedings of the Institution of Mechanical Engineers D. (2010) 224, no. 6, 705–716.
10.1243/09544070JAUTO1228
Web of Science® Google Scholar
13 Kang D. O., Heo S. J., Kim M. S., Choi W. C., and Kim I. H., Robust design optimization of suspension system by using target cascading method, International Journal of Automotive Technology. (2012) 13, no. 1, 109–122, 2-s2.0-80355146555, https://doi.org/10.1007/s12239-012-0010-y.
10.1007/s12239-012-0010-y
Web of Science® Google Scholar
14 Zhao D. and Xue D., A comparative study of metamodeling methods considering sample quality merits, Structural and Multidisciplinary Optimization. (2010) 42, no. 6, 923–938, 2-s2.0-78049408577, https://doi.org/10.1007/s00158-010-0529-3.
10.1007/s00158-010-0529-3
Web of Science® Google Scholar
15 Matheron G., Principals of geostatistics, Economic Geology. (1963) 58, no. 8, 1246–1266.
10.2113/gsecongeo.58.8.1246
CAS Google Scholar
16 Sacks J., Welch W. J., Mitchell T. J., and Wynn H. P., Design and analysis of computer experiments, Statistical Science. (1989) 4, no. 4, 409–435, MR1041765, ZBL0955.62619.
10.1214/ss/1177012413
Google Scholar
17 Lophaven S. N., Nielsen H. B., and Søndergaard J., DACE: A Matlab Kriging Toolbox, Version 2.0, 2002, no. IMMREP-2002-12, Technical University of Denmark, Kongens Lyngby, Denmark.
Google Scholar
18 Ding R., Lin D. K. J., and Wei D., Dual-response surface optimization: a weighted MSE approach, Quality Engineering. (2004) 16, no. 3, 377–385, 2-s2.0-1942468597, https://doi.org/10.1081/QEN-120027940.
10.1081/QEN-120027940
Google Scholar
19 Lin D. K. J. and Tu W., Dual response surface optimization, Journal of Quality Technology. (1995) 27, no. 1, 34–39, 2-s2.0-0029222606.
10.1080/00224065.1995.11979556
Web of Science® Google Scholar
20 McKay M. D., Beckman R. J., and Conover W. J., A comparison of three methods for selecting values of input variables in the analysis of output from a computer code, Technometrics. (1979) 21, no. 2, 239–245, https://doi.org/10.2307/1268522, MR533252, ZBL0415.62011.
10.2307/1268522
Web of Science® Google Scholar

Citing Literature

All articles

An Adaptive Metamodel-Based Optimization Approach for Vehicle Suspension System Design

Abstract

1. Introduction

2. Optimization Problem in Suspension System

3. Adaptive Metamodel-Based Optimization Method

3.1. Metamodeling Method

3.2. Adaptive Metamodel-Based Optimization

3.3. Adaptive Optimization considering Modeling Uncertainty

4. Adaptive Optimization considering Modeling Uncertainty in McPherson Suspension

5. Comparisons and Analysis of the Optimization Results

6. Conclusion

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

An Adaptive Metamodel-Based Optimization Approach for Vehicle Suspension System Design

Abstract

1. Introduction

2. Optimization Problem in Suspension System

3. Adaptive Metamodel-Based Optimization Method

3.1. Metamodeling Method

3.2. Adaptive Metamodel-Based Optimization

3.3. Adaptive Optimization considering Modeling Uncertainty

4. Adaptive Optimization considering Modeling Uncertainty in McPherson Suspension

5. Comparisons and Analysis of the Optimization Results

6. Conclusion

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Related

Information