Volume 2014, Issue 1 925370

Research Article

Open Access

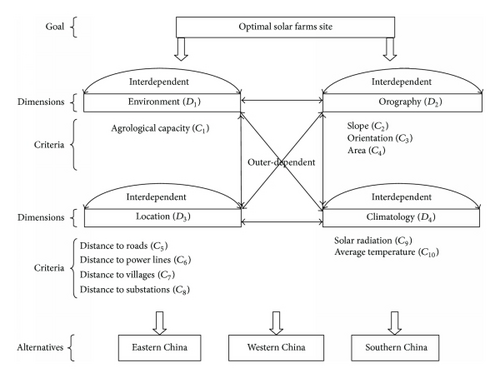
A Hybrid MCDM Model for Improving GIS-Based Solar Farms Site Selection

Chao-Rong Chen,

Chao-Rong Chen

Department of Electrical Engineering, National Taipei University of Technology, Taipei 10608, Taiwan ntut.edu.tw

Search for more papers by this author

Chi-Chen Huang,

Chi-Chen Huang

Department of Electrical Engineering, National Taipei University of Technology, Taipei 10608, Taiwan ntut.edu.tw

Search for more papers by this author

Hung-Jia Tsuei,

Corresponding Author

Hung-Jia Tsuei

[email protected]

orcid.org/0000-0002-2301-753X

Department of Electronic Engineering, National Taipei University of Technology, Taipei 10608, Taiwan ntut.edu.tw

Graduate Institute of Networking and Multimedia, National Taiwan University, Taipei 10617, Taiwan ntu.edu.tw

Search for more papers by this author

Chao-Rong Chen,

Chao-Rong Chen

Department of Electrical Engineering, National Taipei University of Technology, Taipei 10608, Taiwan ntut.edu.tw

Search for more papers by this author

Chi-Chen Huang,

Chi-Chen Huang

Department of Electrical Engineering, National Taipei University of Technology, Taipei 10608, Taiwan ntut.edu.tw

Search for more papers by this author

Hung-Jia Tsuei,

Corresponding Author

Hung-Jia Tsuei

[email protected]

orcid.org/0000-0002-2301-753X

Department of Electronic Engineering, National Taipei University of Technology, Taipei 10608, Taiwan ntut.edu.tw

Graduate Institute of Networking and Multimedia, National Taiwan University, Taipei 10617, Taiwan ntu.edu.tw

Search for more papers by this author

First published: 20 August 2014

https://doi.org/10.1155/2014/925370

Citations: 35

Academic Editor: Ching-Song Jwo

Share a link

Email
Wechat
Bluesky

Abstract

The purpose of this research is to establish a decision model for improving the performance of solar farms. To investigate the interdependent interrelationship and influential weights among criteria for solar farms site selection, a hybrid MCDM model including decision-making trial and evaluation laboratory (DEMATEL) and DEMATEL-based analytic network process (DANP) based on geographical information systems (GIS) is utilized. The empirical results display that there are interdependence and self-effect relationships among criteria via DEMATEL technique. According to the influential network relation map (INRM), the dimension that administrators of solar energy industry should improve first when enhancing the performance of solar farms is orography. In the ten criteria, solar radiation is the most important criterion impacting solar farms site selection, followed by average temperature and distance to villages.

1. Introduction

Among the different types of renewable energy resources, photovoltaic (PV) solar energy is by far the largest exploitable resource for offering more energy in 1 hour to the earth than all of the energy consumed by humans in a whole year [1]. In addition, the PV solar market increased rapidly, because revenues created from the industry will achieve over US$100 billion before 2020 [2]. However, PV solar energy has not achieved adequate maturity, so great efforts are being made regarding lower manufacturing costs and higher efficiencies [3, 4]. Solar farms site selection becomes one of the most important issues for administrators of solar energy industry to maximize the performance of solar farms.

Previous studies regarding solar farms locations focused on considering simply what factors would influence solar farms [5, 6], conveying what factors influence solar farms, and whether the impacts were positive or negative. These discoveries for building a decision model of solar farms site selection have little contribution to it. In addition, although the interrelationship and influential weights among criteria are extremely useful for the administrators to simultaneously consider interdependent multicriteria in real world, literatures concerning these problems are inadequate. Therefore, the purpose of this research is to construct a decision model for enhancing the performance of solar farms. The specific improvement process and influential weights of solar farms site will be explored by a hybrid multiple criteria decision making (MCDM) model based on geographical information systems (GIS).

In order to provide the administrators with the solution to these issues, a hybrid MCDM model combining decision-making trial and evaluation laboratory (DEMATEL) with DEMATEL-based analytical network process (DANP) is employed. The criteria of solar farms site are identified through GIS. According to the survey of experts, this paper adopts DEMATEL technique to probe into the interdependent decision making for constructing the influential network relation map (INRM). The strategies for improving the performance of solar farms can thus be obtained through the influence values of criteria in INRM. Subsequently, to solve the problems with interdependent criteria, the influential weights of solar farms site can be received via DANP derived from the basic concept of analytical network process (ANP) proposed by Saaty [7].

2. Calculation Models and Methods

2.1. Criteria for Solar Farms Site Selection

Industrial site selection is one of the fundamental decisions in the start-up process, expansion, or relocation. GIS are adopted combining with other systems and methods such as systems for decision making (DSS) and the method for MCDM. Synergistic effect is created in conjunction with these tools which contribute to the efficiency and quality of spatial analysis for industrial site selection [8]. Chen and Pang [9] proposed a fuzzy analytic network process (FANP) to investigate critical characteristics of successful PV solar energy industry and examined suitable forms of organization for knowledge management (KM) in order to distribute existing knowledge as well as to create new knowledge. Carrión et al. [10] used an environmental decision-support system (EDSS) for choosing optimal sites for grid-connected PV power plants. The system combined multicriteria analysis and the analytic hierarchy process (AHP) with GIS technology and took into account environment, orography, location, and climate factors in the meantime. Moreover, the combination of GIS and MCDM methods is used to acquire the assessment of the optimal placement of PV solar power plants. The exceptional tool can also be employed to analyze an extensive cartographic and alphanumeric database for simplifying problems to solve and promote the use of multiple criteria [11]. Uyan [12] indicated that solar energy investments have been expanded quickly in recent years. It is a crucial issue for huge solar farms investments to select location for the consideration of terrain, local weathering factors, proximity to high transmission capacity lines, agricultural facilities, and environmental conservation. Multiple criteria evaluation methods are often utilized for various site selection researches. The study determined proper site selection for solar farms by adopting GIS and AHP. Sánchez-Lozano et al. [13] revealed that great position with high percentages of potential solar radiation can host electricity generation plants via PV solar farms. The best plots suitable for installing PV solar farms are identified by employing GIS and classified according to multiple evaluation aspects by means of a multicriteria model.

By literature review, criteria affecting solar farms site selection for improving the performance of solar energy industry are arranged as follows. Solar farms site includes four dimensions: environment (D₁), orography (D₂), location (D₃), and climatology (D₄). To be specific, environment is affected by agrological capacity (C₁); orography is influenced by slope (C₂), orientation (C₃), and area (C₄); location is affected by distance to roads (C₅), distance to power lines (C₆), distance to villages (C₇), and distance to substations (C₈); climatology is influenced by solar radiation (C₉) and average temperature (C₁₀).

2.2. DEMATEL Method

The DEMATEL method is utilized to probe into the problems of interdependent criteria for establishing the INRM [14, 15]. This method has been practically used in decision making problems of various fields, such as vendor selection for recycled material and the organic light emitting diode technology selection [16, 17].

Experts with specialty of technology for PV solar energy and experience from solar energy industry including officials of Bureau of Energy, scholars of energy engineering, and managers of solar industry are invited to help carry out this research. Information required for sufficient evaluation of solar farms site is collected by utilizing interviews and filling suitable questionnaires. In the questionnaires, a scale of 0, 1, 2, 3, and 4 presents the degree from “no influence” to “very high influence.” In addition, the confidence level for experts is tested (97.638%) in this real case of fifteen experts by this research.

The technique is introduced as follows: in the first place, the influence matrix is received by scores. The related experts are asked to indicate the degrees of influence among criteria, that is, to point out how much the criteria affect each other. The influence matrix A can thus be obtained. Secondly, the normalized influence matrix G can be calculated by utilizing (1) and (2) to normalize A:

()

Thirdly, the total influence matrix T can be acquired via the formula T = G + G² + G³ + ⋯+G^q = G(I − G) ⁻¹, when lim_h→∞G^h = [0] _n×n, where I denotes the identity matrix. The fourth step is to use (3) and (4) to construct the INRM through vectors r and d (the sums of the rows and columns separately within the total influence matrix T = [t_ij] _n×n):

()

where the superscript ^′ stands for transpose. If r_i represents the row sum of the ith row in matrix T, then r_i reveals the sum of direct and indirect influences of criterion i on the other criteria. Also, if s_j stands for the column sum of the jth column of matrix T, then s_j displays the sum of direct and indirect effects that criterion j has obtained from the other criteria. Furthermore, when i = j, the sum of the row and column aggregates (r_i + d_i), which presents the giving and received degree of influences; that is, (r_i + d_i) shows the intensity of the important role that the ith criterion plays in the problem. When (r_i − d_i) is positive, the ith criterion influences other criteria. On the contrary, if (r_i − d_i) is negative, other criteria influence the ith criterion (i.e., ith criterion receives influence from other criteria). Therefore, the interdependent interrelationship among criteria can be established by the INRM [18, 19].

2.3. DANP Method

Comparing with [11–13], the advantage of the proposed model is to improve the equal weighting assumption of the traditional method for solving complicated problems in influential weights [16]. ANP was developed by Saaty [7] to reduce the limitations of the AHP and to determine nonlinear and complicated network relationships. Therefore, after investigating the influential relationship, this study integrates DEMATEL with basic concept of ANP (called DEMATEL-based ANP, DANP) to obtain the influential weights of criteria [20]. The DANP includes four steps. First, build the influence network structure based on DEMATEL. Second, find the unweighted supermatrix. The total influence matrix T presented in (5) is derived from DEMATEL:

()

Normalize each level of T_c by using the total degree of influence to obtain

via

()

where

can be calculated through (7) and (8); by the same way,

can be obtained:

()

The unweighted supermatrix can be acquired by adopting the interdependent relationship in group to array

via

()

where W¹¹ is exhibited by (10) and Wⁿⁿ can be obtained in the same way. A blank space or 0 in the matrix stands for independence of the group of criteria or a single criterion in relation to other criteria. Consider

()

The third step is to calculate the weighted supermatrix. The total influence matrix of dimensions T_D is acquired by (12). Utilize the total degree of influence to normalize each level of T_D through (13) to receive

()

The weighted supermatrix W^α can be obtained by normalizing

into the unweighted supermatrix W displayed in

()

Fourthly, receive the influential weights of DANP. The weighted supermatrix W^α is multiplied by itself enough times to calculate the limit supermatrix according to the concept of Markov Chain. The influential weight of criteria can thus be calculated by lim⁡_z→∞(W^α) ^z. The influential weights of DANP are received by the limit supermatrix application W^α with power z, a large enough integer, until the supermatrix W^α has converged and turns a long-term stable supermatrix to acquire the global priority vectors.

3. Results and Discussion

3.1. Establishing the INRM for Comprehending the Interrelationship

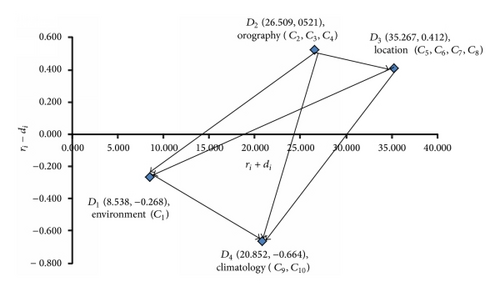
The DEMATEL technique is used to investigate the problems of interdependence and feedback among ten criteria from a literature review. Thereafter, the study construction of the influence network is displayed as Figure 1. The influence matrix A is displayed in the beginning (Table 1). Second, the normalized influence matrix G exhibited in Table 2 can be obtained using (1). Thirdly, the total influence matrix T shown in Table 3 is calculated via (3). The INRM of influential interrelationship for solar farms site is eventually constructed by the vector r and vector d (Table 4) derived from the total influence matrix T shown in Figure 2.

Table 1. The initial influence matrix A.

Criteria	C₁	C₂	C₃	C₄	C₅	C₆	C₇	C₈	C₉	C₁₀
C₁	0.000	2.000	0.467	2.000	3.000	2.600	2.533	2.067	3.467	3.467
C₂	2.000	0.000	2.600	2.533	2.533	2.067	3.000	2.067	3.533	3.067
C₃	2.000	2.600	0.000	2.067	2.533	2.067	2.533	2.533	3.533	3.533
C₄	2.467	2.533	2.533	0.000	2.533	2.533	3.000	3.000	3.533	2.600
C₅	2.533	2.533	2.533	3.000	0.000	2.533	3.000	2.533	3.533	3.067
C₆	2.600	2.067	2.533	2.533	2.533	0.000	3.000	3.000	2.533	2.533
C₇	3.000	2.533	2.067	3.000	3.000	2.533	0.000	2.533	3.000	3.533
C₈	2.067	2.067	2.067	2.067	2.533	2.533	2.533	0.000	2.533	2.533
C₉	3.000	3.067	3.067	3.533	2.533	2.533	2.533	2.533	0.000	4.000
C₁₀	3.467	3.533	3.533	3.067	2.533	2.067	3.067	2.067	4.000	0.000

Note. Consider ; that is, confidence is 97.368%, where u = 15 denotes the number of experts and is the average influence of i criterion on j; n denotes the number of criteria, here n = 10 and n × n matrix.

Table 2. The normalized direct-influence matrix G.

Criteria	C₁	C₂	C₃	C₄	C₅	C₆	C₇	C₈	C₉	C₁₀
C₁	1.336	0.396	0.331	0.409	0.430	0.389	0.436	0.383	0.521	0.505
C₂	0.423	1.357	0.416	0.448	0.441	0.396	0.475	0.407	0.554	0.524
C₃	0.422	0.437	1.336	0.434	0.441	0.395	0.461	0.419	0.553	0.536
C₄	0.451	0.450	0.428	1.385	0.457	0.424	0.492	0.449	0.572	0.529
C₅	0.462	0.459	0.437	0.486	1.387	0.432	0.501	0.444	0.584	0.553
C₆	0.434	0.416	0.408	0.442	0.436	1.326	0.470	0.429	0.518	0.502
C₇	0.475	0.458	0.421	0.485	0.478	0.431	1.408	0.442	0.568	0.564
C₈	0.387	0.384	0.365	0.396	0.404	0.375	0.422	1.306	0.478	0.463
C₉	0.496	0.495	0.471	0.522	0.487	0.450	0.510	0.463	1.504	0.603
C₁₀	0.516	0.516	0.490	0.516	0.495	0.444	0.533	0.457	0.633	1.494

Table 3. The total influence matrix T.

Criteria	C₁	C₂	C₃	C₄	C₅	C₆	C₇	C₈	C₉	C₁₀
C₁	0.336	0.396	0.331	0.409	0.430	0.389	0.436	0.383	0.521	0.505
C₂	0.423	0.357	0.416	0.448	0.441	0.396	0.475	0.407	0.554	0.524
C₃	0.422	0.437	0.336	0.434	0.441	0.395	0.461	0.419	0.553	0.536
C₄	0.451	0.450	0.428	0.385	0.457	0.424	0.492	0.449	0.572	0.529
C₅	0.462	0.459	0.437	0.486	0.387	0.432	0.501	0.444	0.584	0.553
C₆	0.434	0.416	0.408	0.442	0.436	0.326	0.470	0.429	0.518	0.502
C₇	0.475	0.458	0.421	0.485	0.478	0.431	0.408	0.442	0.568	0.564
C₈	0.387	0.384	0.365	0.396	0.404	0.375	0.422	0.306	0.478	0.463
C₉	0.496	0.495	0.471	0.522	0.487	0.450	0.510	0.463	0.504	0.603
C₁₀	0.516	0.516	0.490	0.516	0.495	0.444	0.533	0.457	0.633	0.494

Table 4. The sums of giving and received influences.

Dimensions/criteria	r_i (effects)	d_i (received influences)	r_i + d_i (centrality)	r_i − d_i (causality)
Environment (D₁)	4.135	4.403	8.538	−0.268
Agrological capacity (C₁)	4.135	4.403	8.538	−0.268
Orography (D₂)	13.515	12.994	26.509	0.521
Slope (C₂)	4.441	4.369	8.810	0.072
Orientation (C₃)	4.436	4.103	8.539	0.334
Area (C₄)	4.638	4.523	9.161	0.115
Location (D₃)	17.839	17.427	35.267	0.412
Distance to roads (C₅)	4.746	4.455	9.202	0.291
Distance to power lines (C₆)	4.381	4.063	8.444	0.319
Distance to villages (C₇)	4.731	4.709	9.440	0.023
Distance to substations (C₈)	3.981	4.201	8.181	−0.220
Climatology (D₄)	10.094	10.758	20.852	−0.664
Solar radiation (C₉)	5.001	5.486	10.487	−0.484
Average temperature (C₁₀)	5.092	5.273	10.365	−0.180

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Analytic framework for influence network of solar farms site.

3.2. Calculating Influential Weights of Criteria for Decision Making

DANP is utilized by this study to obtain the level of influential weights of ten criteria for solar farms site selection shown in Tables 5, 6, and 7 based on the construction of the influence network from DEMATEL. The empirical findings present that experts pay more attention to solar radiation (C₉), temperature (C₁₀), and distance to villages (C₇); however, less on orientation (C₃) and distance to power lines (C₆). The outcomes reveal that the level of influential weights is much higher in solar radiation, temperature, and distance to villages. More specifically, solar radiation gets the highest influential weight of 0.12, followed by temperature (0.116) and distance to villages (0.103). Moreover, the level of influential weight of orientation and distance to power lines is relatively lower averaging 0.09.

Table 5. The unweighted supermatrix.

Criteria	C₁	C₂	C₃	C₄	C₅	C₆	C₇	C₈	C₉	C₁₀
C₁	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
C₂	0.348	0.292	0.362	0.356	0.332	0.329	0.336	0.336	0.333	0.339
C₃	0.292	0.341	0.278	0.339	0.316	0.322	0.309	0.319	0.317	0.322
C₄	0.360	0.367	0.360	0.305	0.352	0.349	0.355	0.346	0.351	0.339
C₅	0.262	0.257	0.257	0.251	0.220	0.263	0.272	0.268	0.255	0.257
C₆	0.237	0.230	0.230	0.233	0.245	0.196	0.245	0.249	0.236	0.230
C₇	0.266	0.276	0.269	0.270	0.284	0.283	0.232	0.280	0.267	0.276
C₈	0.234	0.237	0.244	0.246	0.252	0.258	0.251	0.203	0.242	0.237
C₉	0.508	0.514	0.508	0.520	0.514	0.508	0.502	0.508	0.455	0.562
C₁₀	0.492	0.486	0.492	0.480	0.486	0.492	0.498	0.492	0.545	0.438

Table 6. The weighted supermatrix.

Criteria	C₁	C₂	C₃	C₄	C₅	C₆	C₇	C₈	C₉	C₁₀
C₁	0.081	0.096	0.096	0.096	0.099	0.099	0.099	0.099	0.100	0.100
C₂	0.096	0.080	0.099	0.097	0.096	0.095	0.097	0.097	0.099	0.101
C₃	0.080	0.093	0.076	0.093	0.091	0.093	0.089	0.092	0.094	0.096
C₄	0.099	0.100	0.098	0.083	0.102	0.101	0.103	0.100	0.105	0.101
C₅	0.104	0.100	0.100	0.098	0.082	0.099	0.102	0.100	0.097	0.098
C₆	0.094	0.090	0.090	0.091	0.092	0.074	0.092	0.093	0.090	0.088
C₇	0.105	0.108	0.105	0.105	0.107	0.106	0.087	0.105	0.102	0.105
C₈	0.093	0.092	0.095	0.096	0.094	0.097	0.094	0.076	0.092	0.090
C₉	0.126	0.124	0.123	0.126	0.122	0.121	0.119	0.120	0.101	0.124
C₁₀	0.122	0.118	0.119	0.116	0.115	0.117	0.118	0.117	0.121	0.097

Table 7. The stable matrix of DANP.

Criteria	C₁	C₂	C₃	C₄	C₅	C₆	C₇	C₈	C₉	C₁₀
C₁	0.097	0.097	0.097	0.097	0.097	0.097	0.097	0.097	0.097	0.097
C₂	0.096	0.096	0.096	0.096	0.096	0.096	0.096	0.096	0.096	0.096
C₃	0.090	0.090	0.090	0.090	0.090	0.090	0.090	0.090	0.090	0.090
C₄	0.099	0.099	0.099	0.099	0.099	0.099	0.099	0.099	0.099	0.099
C₅	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098
C₆	0.090	0.090	0.090	0.090	0.090	0.090	0.090	0.090	0.090	0.090
C₇	0.103	0.103	0.103	0.103	0.103	0.103	0.103	0.103	0.103	0.103
C₈	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092
C₉	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120
C₁₀	0.116	0.116	0.116	0.116	0.116	0.116	0.116	0.116	0.116	0.116

When comparing criteria within dimension, the influential weight of agrological capacity is 0.097 in the dimension of environment (D₁). Experts think area is the most important criterion in the dimension of orography (D₂). As for location (D₃), the influential weight of distance to villages is the highest. Solar radiation is regarded by experts as the most important criterion in the dimension of climatology (D₄). Received results present that solar radiation (ranked top one) is the last criterion which can be neglected when improving the performance of solar farms. Experts are much concerned with dimension of climatology (D₄) in that the mean (0.118) of its criteria is much higher than others in the standpoint of dimensions.

In addition, this study collects comparative data from three different regions of China for empirical analysis by the purposed model to reveal the improving of the performance of solar farms site, because China has one of the biggest markets of solar industry in the world. Table 8 shows the integrated values by utilizing simple additive weighting (SAW) method to receive the total performances of three regions selected in China. The empirical results present that western China has the highest total performance level. It is followed by eastern and southern China with this regard. Therefore, decision makers of solar farms site selection are suggested to take western China as an example when improving the performance of solar farms site according to the decision model provided by this research.

Table 8. Influential weights of solar farms site and performances of selected regions.

Dimensions/criteria	Local weights	Global weights	Eastern China	Western China	Southern China
Environment (D₁)	0.097		3.667	5.667	2.400
Agrological capacity (C₁)	1.000	0.097	3.667	5.667	2.400
Orography (D₂)	0.285		4.529	6.051	3.043
Slope (C₂)	0.336	0.096	3.667	5.333	2.800
Orientation (C₃)	0.315	0.090	6.400	8.400	4.400
Area (C₄)	0.348	0.099	3.667	5.600	2.400
Location (D₃)	0.383		3.548	5.144	3.336
Distance to roads (C₅)	0.256	0.098	3.333	5.667	3.200
Distance to power lines (C₆)	0.234	0.090	3.800	6.400	4.200
Distance to villages (C₇)	0.270	0.103	3.667	3.333	3.667
Distance to substations (C₈)	0.240	0.092	3.400	5.400	2.267
Climatology (D₄)	0.235		5.193	7.336	4.087
Solar radiation (C₉)	0.508	0.120	4.800	7.467	3.333
Average temperature (C₁₀)	0.492	0.116	5.600	7.200	4.867

Total performances	—	—	4.227	5.969	3.339

3.3. Implication and Discussion

Discussion of empirical results and innovation strategies for improving the performance for solar farms site is presented as follows. In the first place, the influential relationships within solar farms suggest that what administrators should improve first is orography (D₂) for enhancing the performance for solar farms based on INRM built by DEMATEL. It is meaningful to improve other dimensions after having an excellent geomorphological solar farms base. It should be well located on an even and facing south land to take advantage of natural resource efficiently.

Second, the most important criterion found by DANP when improving solar farms is solar radiation (C₉), whose influential weight equals 0.12. It plays a significant role in the effective functioning of a prosperous solar energy industry. To follow the arc of the sun for generating the optimal amount of power, solar panels are typically mounted on rotating towers. Therefore, solar farms should better situate panels to make the most of the available solar radiation.

4. Conclusions

The proposed hybrid MCDM model based on GIS can be applied by managers of solar energy industry worldwide. They can adjust the influential weights of the ten criteria according to the situations of various countries to obtain valuable information for decision making when improving the performance of solar farms. Moreover, they can select a potential base to evaluate if it is suitable or not.

Furthermore, only few preceding study attempts are concerned about the interdependent interrelationship among criteria and the influential weights of criteria. This study thus proposes a hybrid MCDM model based on GIS and explores the perspectives of employing experts for examining these issues for solar farms. Associating past theoretical research with opinions of professional and experienced experts makes the proposed model a more suitable tool for improving solar farms site selection. It is not provided by preceding study attempts. This study mainly utilizes a hybrid MCDM model based on GIS for exploring solar farms site, so some critical factors (e.g., incentive from government and purchase price for electricity from utility) can be included by taking extra dimensions into consideration to make the research more complete in the future.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

This work was supported in part by the National Science Council in Taiwan, under the project title: Caltech-Taiwan Collaboration on Energy Research-Uncertainty Mitigation for Renewable Energy Integration, Project no. NSC 101-3113-P-008-001.

References

1 Lewis N. S. and Nocera D. G., Powering the planet: chemical challenges in solar energy utilization, Proceedings of the National Academy of Sciences of the United States of America. (2006) 103, no. 43, 15729–15735, https://doi.org/10.1073/pnas.0603395103, 2-s2.0-33750458683.
Google Scholar
2 MOEA, The analysis and investment opportunities in photovoltaic industry, Department of Investment Services, Ministry of Economic Affairs (MOEA), 2008, http://www.dois.moea.gov.tw/.
Google Scholar
3 Socorro García-Cascales M., Teresa Lamata M., and Miguel Sánchez-Lozano J., Evaluation of photovoltaic cells in a multi-criteria decision making process, Annals of Operations Research. (2012) 199, no. 1, 373–391, ZBL1251.90217, 2-s2.0-84866113542, https://doi.org/10.1007/s10479-011-1009-x.
Google Scholar
4 Parida B., Iniyan S., and Goic R., A review of solar photovoltaic technologies, Renewable and Sustainable Energy Reviews. (2011) 15, no. 3, 1625–1636, https://doi.org/10.1016/j.rser.2010.11.032, 2-s2.0-78650976196.
Web of Science® Google Scholar
5 Bhaskar M. A., Dash S. S., Magdal R. et al., Application of integrated wind energy conversion system (WECS) and photovoltaic (PV) solar farm as STATCOM to regulate grid voltage during night time, Energy Procedia. (2012) 14, 1536–1541, https://doi.org/10.1016/j.egypro.2011.12.1129.
Google Scholar
6 Hodson H., Giant solar farm uses molten salt to keep power coming, New Scientist. (2014) 222, no. 2965.
Google Scholar
7 Saaty T. L., Decision Making with Dependence and Feedback: The Analytic Network Process, 1996, RWS Publications, Pittsburgh, Pa, USA.
Google Scholar
8 Rikalovic A., Cosic I., and Lazarevic D., GIS based multi-criteria analysis for industrial site selection, Procedia Engineering. (2014) 69, 1054–1063.
Google Scholar
9 Chen H. H. and Pang C., Organizational forms for knowledge management in photovoltaic solar energy industry, Knowledge-Based Systems. (2010) 23, no. 8, 924–933, https://doi.org/10.1016/j.knosys.2010.06.008, 2-s2.0-77957896430.
Google Scholar
10 Carrión J. A., Estrella A. E., Dols F. A., Toro M. Z., Rodríguez M., and Ridao A. R., Environmental decision-support systems for evaluating the carrying capacity of land areas: optimal site selection for grid-connected photovoltaic power plants, Renewable and Sustainable Energy Reviews. (2008) 12, no. 9, 2358–2380, https://doi.org/10.1016/j.rser.2007.06.011, 2-s2.0-50949090479.
Web of Science® Google Scholar
11 Sánchez-Lozano J. M., Teruel-Solano J., Soto-Elvira P. L., and Socorro García-Cascales M., Geographical Information Systems (GIS) and Multi-Criteria Decision Making (MCDM) methods for the evaluation of solar farms locations: case study in south-eastern Spain, Renewable and Sustainable Energy Reviews. (2013) 24, 544–556, https://doi.org/10.1016/j.rser.2013.03.019, 2-s2.0-84876933357.
Web of Science® Google Scholar
12 Uyan M., GIS-based solar farms site selection using analytic hierarchy process (AHP) in Karapinar region Konya/Turkey, Renewable and Sustainable Energy Reviews. (2013) 28, 11–17, https://doi.org/10.1016/j.rser.2013.07.042, 2-s2.0-84881348888.
Web of Science® Google Scholar
13 Sánchez-Lozano J. M., Antunes C. H., García-Cascales M. S., and Dias L. C., GIS-based photovoltaic solar farms site selection using ELECTRE-TRI: evaluating the case for Torre Pacheco, Murcia, Southeast of Spain, Renewable Energy. (2014) 66, 478–494, https://doi.org/10.1016/j.renene.2013.12.038.
Web of Science® Google Scholar
14 Chen C. H. and Tzeng G. H., Creating the aspired intelligent assessment systems for teaching materials, Expert Systems with Applications. (2011) 38, no. 10, 12168–12179, https://doi.org/10.1016/j.eswa.2011.03.050, 2-s2.0-79958004979.
Google Scholar
15 Fontela E. and Gabus A., The DEMATEL Observer, DEMATEL 1976 Report, 1976, Battelle Geneva Research Centre, Geneva, Switzerland.
Google Scholar
16 Hsu C.-., Wang F., and Tzeng G., The best vendor selection for conducting the recycled material based on a hybrid MCDM model combining DANP with VIKOR, Resources, Conservation and Recycling. (2012) 66, 95–111, https://doi.org/10.1016/j.resconrec.2012.02.009, 2-s2.0-84864440540.
Web of Science® Google Scholar
17 Shen Y., Lin G. T. R., and Tzeng G., Combined DEMATEL techniques with novel MCDM for the organic light emitting diode technology selection, Expert Systems with Applications. (2011) 38, no. 3, 1468–1481, https://doi.org/10.1016/j.eswa.2010.07.056, 2-s2.0-78049530327.
Google Scholar
18 Liou J. J. H., Tzeng G., and Chang H., Airline safety measurement using a hybrid model, Journal of Air Transport Management. (2007) 13, no. 4, 243–249, https://doi.org/10.1016/j.jairtraman.2007.04.008, 2-s2.0-34249784502.
Google Scholar
19 Tzeng G., Chiang C., and Li C., Evaluating intertwined effects in e-learning programs: A novel hybrid MCDM model based on factor analysis and DEMATEL, Expert Systems with Applications. (2007) 32, no. 4, 1028–1044, https://doi.org/10.1016/j.eswa.2006.02.004, 2-s2.0-33751418314.
Web of Science® Google Scholar
20 Ou Yang Y. P., Shieh H. M., Leu J. D., and Tzeng G. H., A novel hybrid MCDM model combined with DEMATEL and ANP with applications, International Journal of Operations Research. (2008) 5, no. 3, 160–168.
Google Scholar

Citing Literature

All articles

A Hybrid MCDM Model for Improving GIS-Based Solar Farms Site Selection

Abstract

1. Introduction

2. Calculation Models and Methods