International Journal of Manufacturing Engineering
Volume 2014, Issue 1 921081
Research Article
Open Access

Experimental Investigation and Multiobjective Optimization of Turning Duplex Stainless Steels

Rastee D. Koyee, 

Corresponding Author

Rastee D. Koyee

Institute for Machine Tools, University of Stuttgart, Holzgartenstraße 17, 70174 Stuttgart, Germany uni-stuttgart.de

Search for more papers by this author
Uwe Heisel, 

Uwe Heisel

Institute for Machine Tools, University of Stuttgart, Holzgartenstraße 17, 70174 Stuttgart, Germany uni-stuttgart.de

Search for more papers by this author
Siegfried Schmauder, 

Siegfried Schmauder

IMWF, University of Stuttgart, Pfaffenwaldring 32, 70569 Stuttgart, Germany uni-stuttgart.de

Search for more papers by this author
Rocco Eisseler, 

Rocco Eisseler

Institute for Machine Tools, University of Stuttgart, Holzgartenstraße 17, 70174 Stuttgart, Germany uni-stuttgart.de

Search for more papers by this author
First published: 03 December 2014
https://doi.org/10.1155/2014/921081
Citations: 15
Academic Editor: Godfrey C. Onwubolu

Abstract

This paper addresses experimental investigations of turning EN 1.4462 and EN 1.4410 duplex stainless steel grades with multilayer coated carbide inserts. Single-point wet and dry longitudinal turning tests of cylindrical bars are conducted; cutting forces, effective cutting powers, and tool wear are measured. The parametric influences of cutting speed, feed rate, and process conditions on the cutting performances such as resultant cutting force, specific effective cutting power, and flank wear are analyzed and proper conclusions are drawn. Nature-inspired metaheuristic bat algorithm is employed to handle the multiobjective optimization of the conflicting performances. Finally, the optimum cutting condition for each process condition can be selected from calculated Pareto optimal fronts by the user according to the planning requirements.

1. Introduction

Duplex stainless steels (DSSs) can be defined as a family of stainless steels whose structures are approximately 50% austenite and 50% ferrite, and its physical properties are a combination of the ferritic and the austenitic grades. In addition to their relatively low cost, they combine the best attributes of both austenitic and ferritic stainless steels which provide high strength and ductility with good resistance to corrosion (including stress corrosion cracking). Therefore, they are most commonly used when a combination of high mechanical strength and high corrosion resistance is required and are increasingly seen as an attractive alternative to the conventional stainless steels. However, owing to their high tensile and yield strength (roughly twice the yield strength of their counterpart austenitic grades, see Table 1), high work hardening rate, low thermal conductivity, high fracture toughness, strong tendency to form the built-up edge (BUE), and relatively high austenite and nitrogen content, modern duplex stainless steels are regarded as poorly machinable materials [1].

Table 1. Workpiece materials properties.
Chemical composition %weight EN 1.4462 EN 1.4410
C 0.018 0.015
Cr 22.42 24.92
Ni 5.44 6.91
Mo 3.12 4.06
Mn 0.84 0.75
Si 0.37 0.25
N 0.18 0.3
P 0.025 0.021
S 0.0033 0.0007
  
Mechanical properties
Yield strength (MPa) 514 579
Tensile (MPa) 737 826
Hardness (BHN) 212 236
Elongation (%) 41 40

Over the past several years, few researchers have investigated the machining of duplex stainless steels. For instance, Bordinassi et al. studied the main effects of the turning in the superficial integrity of the duplex stainless steel ASTM A890-Gr6A. Their findings have shown that the smaller feed rate, smaller cutting speed, and the greater cutting depth provided the smaller values for the tensile residual stress, the smaller surface roughness, and the greater microhardness [2]. Królczyk et al. examined the influence of cutting parameters on surface roughness after DSS turning process. Their results have clearly showed that the feed rate was the main influencing factor on the surface roughness [3]. Królczyk et al. determined the coated carbide tool life and drew the tool wear curve when machining DSS. Their results have confirmed no effect of cutting speed and cooling on metallographic structure and designated the optimum cutting speed between 130 and 150 m/min and [4]. Nomani et al. have conducted machinability tests on duplex alloys SAF 2205 and SAF 2507, while employing austenite stainless steel 316L as a benchmark during drilling. Both duplex alloys displayed poorer machinability responses, with 2507 being worst [5]. Oliveira Jr. et al. have studied the turning operation of SAF 2507 and its influence on the alloy’s corrosion resistance in practical applications. Their results have indicated that turning with PVD-coated inserts under high-pressure cooling resulted in long tool lives, good workpiece roughness, and high corrosion resistance of the material after machining. The most frequent wear mechanism found during the tests was notch wear, while the main tool wear mechanism was attrition [6]. Philip Selvaraj et al. have optimized dry turning parameters of two different grades of nitrogen alloyed duplex stainless steel by using Taguchi method. Their results revealed that the feed rate is the most significant parameter influencing the surface roughness and cutting force. On the other hand, the cutting speed was identified as the most significant parameter influencing the tool wear [7].

In this paper, multiobjective bat algorithm (MOBA) is applied to optimize the conflicting turning performances such as resultant cutting force, specific effective cutting power, and maximum flank wear. The algorithm suggests sets of optimum solutions for the parameter setting of DSS turning process. The models of conflicting performances were obtained from experimental data. The rest of this paper is organized as follows. The description of MOBA is introduced in Section 2. Discussions of the obtained experimental results are presented in Section 3. Modeling of performance characteristics is described in Section 4. Results of MOBA are shown in Section 5 and some conclusions are given in Section 6.

2. Multiobjective Bat Algorithm (MOBA)

Nature-inspired metaheuristic algorithms are based on strategies that try to imitate the behavior observed in species found in nature to update a population of candidates to solve optimization problems. They have contributed significantly to the development of new optimization techniques. These algorithms can be classified as population-based and trajectory-based. BA is a population-based swarm intelligence algorithm which is inspired by the echolocation of microbats. Echolocation is an advanced hearing based navigation system used by bats and some other animals to detect objects in their surroundings by emitting a sound to the environment. In general echolocation calls are characterized by three features, namely, pulse frequency, pulse emission rate, and loudness (intensity). In general the frequency φ in a range [φmin⁡, φmax⁡] corresponds to a range of wavelengths [Ωmin⁡, Ωmax⁡]. For example, a frequency range of [20 kHz, 500 kHz] corresponds to a range of wavelengths from 0.7 mm to 17 mm in reality. Obviously, one can choose the ranges freely to suit different applications. In order to develop a standard bat algorithm, the following approximate or idealized rules are applied.
  • (a)

    All bats use echolocation to sense distance, and they also “know” the difference between food/prey and background barriers in some magical way.

  • (b)

    Bats fly randomly with velocity vi at position xi with a frequency φmin⁡, varying wavelength, and loudness A0 to search for prey. They can automatically adjust the wavelength (or frequency) of their emitted pulses and adjust the rate of pulse emission r ∈ [0,1], depending on the proximity of their target.

  • (c)

    Although the loudness can vary in many ways, we assume that the loudness varies from a large (positive) A0 to a minimum constant value Amin⁡.

For the bats in simulations, we have to define the rules how their positions xi and velocities vi in a d-dimensional search space are updated. The new solutions xti and velocities vti at time step t are given by
()
where β ∈ [0,1] is a random vector drawn from a uniform distribution. Here x* is the current global best location (solution) which is located after comparing all the solutions among all the n bats at each iteration t. Based on the above approximations and idealization, the basic steps of the multiobjective bat algorithm (MOBA) can be summarized as the pseudocode shown in Algorithm 1.
    Algorithm 1: Multiobjective bat algorithm (MOBA) [10].

  • Objective functions f1(x), …, fK(x), x =

  • Initialize the bat population xi (i = 1,  2, …, n) and vi

  • for  j = 1 to N (points on Pareto fronts)

  •         while (t < Max number of iterations)

  •                 Generate new solutions and update by (1)

  •                 if (rand > ri)

  •                         Random walk around a selected best solution

  •                 end if

  •                 Generate a new solution by flying randomly

  •                 if  (rand < Ai & f(xi) < f(x*))

  •                         Accept the new solutions,

  •                         and increase ri& reduce Ai

  •                 end if

  •                 Rank the bats and find the current best x*

  •         end while

  •         Record x* as a non-dominated solution

  • end

  • Postprocess results and visualization

2.1. Pareto Optimality

The concept of Pareto optimum was formulated by Vilfredo Pareto in the XIX century and constitutes by itself the origin of research in multiobjective optimization. A solution vector u = (u1, …, un) T ∈ F is said to dominate another vector v = (v1, …, vn) T if and only if ui ≤ vi for all i ∈ {1, …, n} and ∃i ∈ {1, …, n} : ui < vi. In other words, no component of u is larger than the corresponding component of v, and at least one component is smaller. Similarly, we can define another dominance relationship ≼ by
()
It is worth pointing out that, for maximization problems, the dominance can be defined by replacing ≺ with ≻. Therefore, a point x* ∈ F is called a nondominated solution if no solution can be found that dominates it [8]. The Pareto front PF of a multiobjective can be defined as the set of nondominated solutions so that
()
or in terms of the Pareto optimal set in the search space
()
where G = (G1, …, GK) T. To obtain a good approximation to Pareto front, a diverse range of solutions should be generated using efficient techniques [9].

3. Materials and Methods

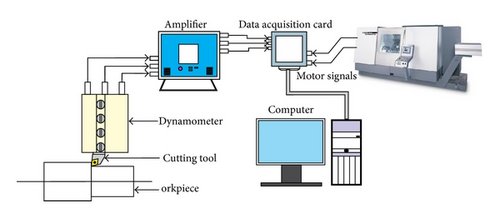
Full-factorial cutting tests are carried out on a CNC lathe (CTX 420 Linear V5) with maximum drive power 25 kW and a speed range of 35–7000 rpm. The workpiece materials for turning tests were standard DSS EN 1.4462 and super DSS EN 1.4410. Their chemical compositions and mechanical properties are given in Table 1.

The cutting tools used in the tests were made by Sandvik Coromant AB, Sweden. The solid carbide inserts were of type CNMG 120408-MM 2025. The coating consists of 5.5 μm CVD TiCN-Al2O3-TiN layers on a substrate which features excellent resistance to both mechanical and thermal shock. The triple coating consists of a 2.5 µm thick TiCN at the bottom followed by a 2 µm multilayer TiN/Al2O3 at the middle and finally a thin (~1 µm) outer coating of TiN on top. The inserts were mounted on a right hand style PCLNL-2525M-12 ISO type tool holder with tool geometry as follows: including angle = 80°, back rake angle = −6°, clearance angle = 5°, approach angle = 95°, and cutting edge radius ≈ 40 μm. The cutting and process conditions are given in Table 2. It has been designed to study the effects of the workpiece materials, process, and cutting conditions on the constants in Kienzle’s cutting force model.

Table 2. Cutting and process conditions.
Cutting speed, m/min 100, 180
Feed rate, mm/rev 0.15, 0.2, 0.25, 0.3, 0.35, 0.4
Cutting depth, mm 1
Process condition Dry, wet
The width of maximum flank wear (VBmax⁡) was periodically measured during progressive tool wear experiments using an optical microscope after every cutting pass of machining operation. The criterion for tool life was VBmax⁡ = 0.6 mm or catastrophic tool failure of the tool edge. During the turning tests, the main cutting force (Fc), axial force (Fa), and radial force (Fr) were measured using a Kistler type 9129A three-component piezoelectric dynamometer, which was connected to a charged Kistler type 5070A amplifier and personal computer through an analog to digital converter card. The resultant cutting force is calculated using
()
Thereafter, specific cutting pressures such as main kc, feed kf, and radial kr are calculated using the following equations:
()
where f is the feed rate and ap is the cutting depth. The effective cutting power (Peff.) component of the motor is always proportional to the torque emitted by the motor; therefore it is often used as a signal within the control system for quantifying the motor load. During the course of each cutting test, the electrical current consumed by the machine tool was measured from the external effective-power modules which were installed between the frequency convertor and the motor. In the present study, the range of energy requirements at the drive motor of the machine tool while turning DSS is estimated using the specific effective cutting power which can be calculated using the following formula:
()
where U is the line voltage in volts, I is the line current in ampere, cos⁡⁡φ is the power factor, and vc is the cutting speed. The experimental setup is shown in Figure 1. In the present research, high-resolution thermographic camera of brand VarioCam head Hires 640 by InfraTec is used to film the chip formation and measure the chip temperature at a resolution of 640 × 480 pixels.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Diagram of the experimental setup.

4. Results and Discussion

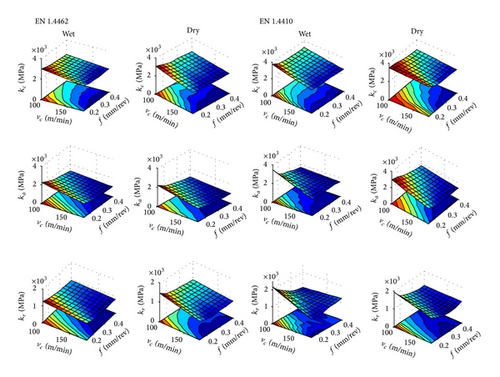
4.1. Specific Cutting Pressure

The specific cutting pressure is often considered as an indication of the machinability of a given work material. The higher the specific cutting pressure is, the lower the machinability of the work material is. The specific cutting pressures for turning EN 1.4462 and EN 1.4410 were calculated from the cutting data employing (6) and the results are shown in Figure 2. Based on a quick review of the results,
  • (1)

    no drastic difference between the cutting pressures of dry and wet conditions was observed. However, overall wet machining shows an improvement in the machining performance through lower cutting pressures;

  • (2)

    specific cutting pressures when machining EN 1.4462 DSS were seen lower than the specific cutting pressures when machining EN 1.4410. Therefore, it can be predicted that the machinability index EN 1.4410 will be smaller than the machinability index of EN 1.4462;

  • (3)

    the cutting pressures generally showed a decreasing trend with increasing cutting speed and feed rate (see Figure 2). As it can be seen in this figure, the maximum cutting pressures occur at low cutting speeds and low feed rates. Thus, in order to achieve low cutting pressures, machining process should be done in high cutting speeds and high feed rates;

  • (4)

    modified Kienzle formula can be applied to evaluate the parametric effects of cutting conditions on the cutting forces as follows:

    ()

  •  

    where F represents the described cutting and resultant forces, k1.1 is the specific cutting pressure for 1 mm2 cross-sectional area of the cut, and a and b are constants. The model fitting has employed the least square method. Summary of models coefficients is listed in Table 3.

To avoid misleading conclusions, the adequacy of the fitted models should be checked. Therefore, analysis of variance (ANOVA) for 95% a level of confidence was performed in order to estimate the predictive accuracy of the models and to determine the relative significances of the different factors using Matlab. From the ANOVA shown in Table 4, it is apparent that almost all correlation coefficients are near to 1, showing that significant terms have been included in the model and that the model is capable of predicting the responses, P value estimators are all close to zero (much lower than 0.05 corresponding to the confidence interval) which show the significant effect of factors on the corresponding response, and F-values are much larger than 1, which indicate that factors have a significant effect on the response. Moreover, variations of cutting force, feed force, and radial force towards cutting speed and feed rate are studied in dry and wet machining separately. It should be noted that the average k1.1 at wet cutting is generally seen 5% lower than k1.1 at dry cutting and k1.1 of turning EN 1.4410 is generally 25.281% higher than k1.1 of turning EN 1.4462. These results clearly indicate the impact of process conditions and workpiece materials on the amount of energy required to cut 1 mm2 chip cross-sections at 100 m/min.
Table 3. Summary of the models coefficients.
Model Proc. cond. EN 1.4462 EN 1.4410
k1.1 a b k1.1 a b
Fc Dry 2367 −0.28 0.1 2920 −0.29 0.08
Wet 2215 −0.26 0.13 2471 −0.26 0.19
  
Ff Dry 852 −0.48 0.47 1182 −0.41 0.47
Wet 737 −0.49 0.53 1126 −0.64 0.5
  
Fr Dry 741 −0.27 0.23 921 −0.22 0.32
Wet 899 −0.46 0.18 908 −0.23 0.3
  
R Dry 2550 −0.32 0.2 3145 −0.31 0.21
Wet 2431 −0.32 0.22 2811 −0.35 0.28
Table 4. Analysis of variance for cutting force models.
Proc. cond. EN 1.4462 EN 1.4410
R2 F-value P value R2 F-value P value
Dry 0.99 0.99 8430 7.8E − 16 0.99 0.99 5310 6.25E − 15
Wet 0.99 0.98 4010 2.2E − 14 0.99 0.99 7900 1.05E − 15
Dry 0.96 0.95 1660 1.2E − 12 0.84 0.80 350 1.24E − 09
Wet 0.94 0.92 1130 6.6E − 12 0.95 0.93 949 1.43E − 11
Dry 0.97 0.96 1720 9.9E − 13 0.73 0.67 159 4.14E − 08
Wet 0.96 0.95 1060 8.8E − 12 0.88 0.85 457 3.76E − 10
Dry 0.98 0.98 3870 2.6E − 14 0.96 0.95 1120 6.73E − 12
Wet 0.98 0.97 2250 3E − 13 0.98 0.97 2850 1.02E − 13
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Computed specific cutting pressures.

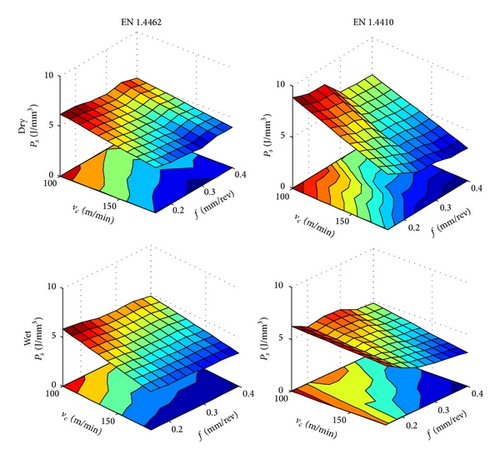
4.2. Specific Effective Cutting Power (Ps)

It has been suggested that more than 90% of environmental impact from machine tools is due to electrical energy consumption [11]. Therefore, minimizing this consumption is supposed to significantly improve the sustainability performance of manufacturing systems. To achieve this, the estimation of the energy consumed in machining operation should be accomplished through calculation of the specific effective cutting power (see (7)), which can be defined as the amount of the machine-tool energy required to remove a certain volume of the material. Beside the consumed cutting energy in chip formation, it is comprised of the energy consumed by varieties of machine-tool functions such as workpiece handling and movement, cutting fluid system, chip removal, and tool changing. The specific effective cutting power is supposed to depend on the machinability of the work material, which takes into account the material properties, process conditions, and cutting conditions. The influences of cutting parameters vc and f and process conditions on the specific effective cutting power are shown in Figure 3, from which, the following observations can be made.
  • (1)

    Specific effective cutting power is inversely proportional to the cutting speed and feed rate.

  • (2)

    Compared to the dry cutting, the wet cutting of EN 1.4462 and EN 1.4410 has shown lower values of Ps by 10.82% and 18.81%, respectively. This is mainly attributed to the lower cutting forces in wet cutting. Therefore, the advantage of employing wet cutting when machining DSSs overtakes its disadvantage of being more energy consumable due to the operation of the coolant pump.

  • (3)

    Average Ps when machining EN 1.4410 is 12.3% higher than the average Ps when machining EN 1.4462. This result is expected as the latter has inferior mechanical properties and higher percentage of chip breaking constituents such as sulfur and phosphorus (see Table 1).

  • (4)

    The effect of the process parameters on the Ps results can be modelled using the nonlinear model:

    ()

  •  

    where C1–3 are the model coefficients. The values of model coefficients and the check of adequacy of the models for each turning case are shown in Table 5. It can be seen from this table that the R2 values are high and close to 1, which are usually desirable. The large model F-values and small mode P values imply that the models are significant. Therefore, results from the statistical analyses indicate that the developed mathematical models can be successfully applied for predicting the Ps.

  • (5)

    The mean specific cutting pressure can be estimated by the equation:

    ()

  •  

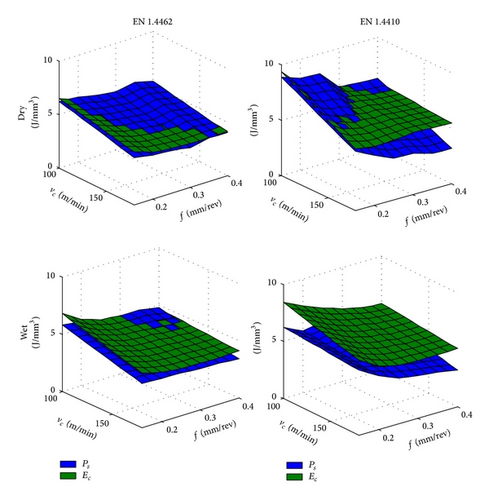
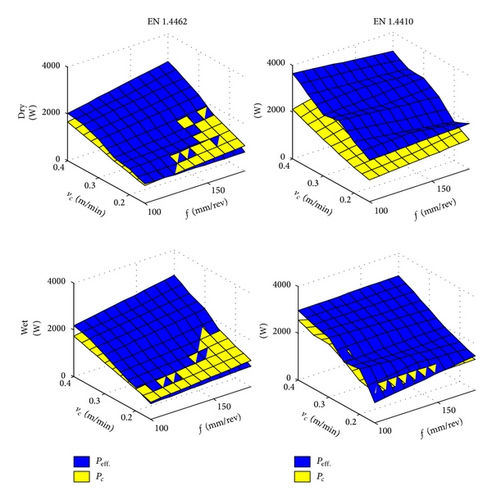
    when cutting EN 1.4462 and EN 1.4410 were found to be 79.7% and 60.72% higher than corresponding Ps values (see Figure 4).

  • (6)

    The comparison between the effective cutting power (Peff.) and the overall consumed cutting power (Pc) (see Figure 5) calculated by (11) has revealed that the average Peff. is 8.965% and 33.3195% higher than average Pc for cutting both EN 1.4462 and EN 1.4410, respectively. Results have also showed that the average Pc in wet cutting EN 1.4462 and EN 1.4410 were 2.9931% and 8.27% lower than the corresponding dry cutting:

    ()

Table 5. Ps model coefficients and check of the models adequacy.
Coeff. EN 1.4462 EN 1.4410
Dry Wet Dry Wet
C1 4.859 4.217 4.183 3.329
C2 −0.595 −0.631 −1.055 −0.445
C3 1.128 1.163 1.421 1.360
  
Check of models adequacy
R2 0.972 0.989 0.973 0.874
0.966 0.987 0.968 0.845
F-value 3.35E + 03 7.70E + 03 1.06E + 03 6.29E + 04
P value 4.99E − 14 1.17E − 15 8.58E − 12 9.05E − 11
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Specific effective cutting power.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Comparison between Ps and Ec.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Comparison between Pc and Peff..

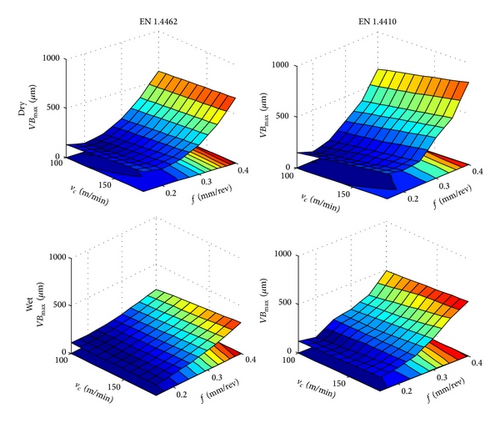
4.3. The Width of Maximum Flank Wear (VBmax⁡ )

The impacts of cutting parameters vc and f and process conditions on the VBmax⁡ are shown in Figure 6 and the summary of the findings is presented below.
  • (1)

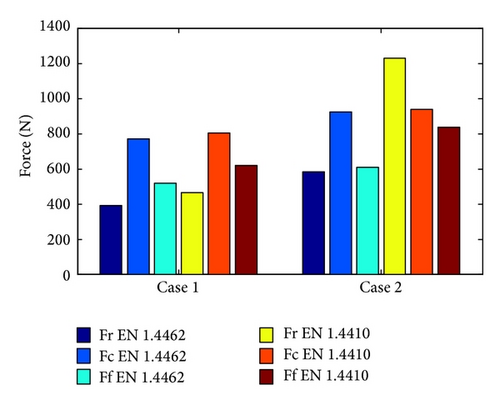
    Based on the observations of tool wear behavior with respect to time during dry machining of DSSs, EN 1.4410 is considered more difficult-to-machine than EN 1.4462. For instance, machining EN 1.4410 at cutting speed value of 180 m/min and feed rate value of 0.35 mm/rev has resulted in significantly higher wear rate and thus shorter tool life, higher cutting temperature, higher cutting forces, and higher energy consumption than machining EN 1.4462 (see Figure 7). Figure 8 shows the average value of recorded cutting forces in dry conditions over 60 sec and 320 sec of machining EN 1.4462 and 20 sec and 40 sec of machining EN 1.4410.

  •  

    An increasing trend in all cutting forces (main, feed, and radial) over time was observed. However, the largest percentage of cutting force increase was recorded in radial cutting force with 32.933% and 164.34% for machining EN 1.4462 and EN 1.4410, respectively. From this perspective, the most suitable parameter to monitor and correlate with progressive tool wear during machining is the radial cutting force component.

  • (2)

    The illustration of typical wear forms when machining DSSs are shown in Figure 9. The following can be seen.

    • (a)

      Severe adhesion between the chip and the rake face of the tool (BUE) was visible throughout the worn crater area. This is believed to be attributed to the high pressure and temperature encountered in machining ductile materials such as DSSs.

    • (b)

      Regardless of the adopted process conditions, chipping of the cutting edge at high feed rate was often observed, which has significantly contributed to acceleration of tool failure. Heavy load and impact when the tool entered and/or extracted the workpiece are considered to be the main reasons behind this phenomenon.

    • (c)

      The most dominant tool wear mode under low cutting speed conditions was the notch wear which was typically located near the depth of cut line. These notches act as stress and temperature raisers of the already high mechanical strength, strain hardening rate, fracture toughness, and low conductivity DSSs chips. Flaking occurrence because of the concentrated thermal load is more possible there. Ultimately, the combination of notch wear and flaking caused the cutting edge to fail abruptly.

    • (d)

      Another form of the main cutting edge damage is caused by the unfavorable chip morphology and chip flow (see Figure 10). Cutting DSSs at low cutting speed and feed rate has contributed to the formation of strong ribbon and snarled chips with dominant side-curl flow. The chips were entangled around the cutting tool, tool post, and workpiece and damaged to the cutting edge and the workpiece surface. The damage is often propagated along the main cutting edge of the tool with cutting time and had exceeded 5 mm length of damage in feed rate ranges of 0.15–0.20 mm/rev.

    • (e)

      In addition to the combined notching and flaking effects, nearly equal proportions of soft ferrite and hard austenite grains in the DSS structure make the cutting tool alternate cutting between soft and hard grains; this leads to an automatic tendency to initiate chatter in the cutting system and promote the catastrophic failure of the cutting tools.

  • (3)

    To model VBmax⁡, an empirical formula described by (8) is applied as follows:

    ()

  •  

    where λ1–3 are model constants. To check the adequacy of derived models, ANOVA for 95% confidence interval has been applied. Table 6 summarizes the values of coefficients and adequacy criterion. It can be seen that high correlation coefficients are existing between the experimental and predicted VBmax⁡ values and high model F-values, and low model P values (≪0.05) confirm the significance of the models.

Table 6. VBmax⁡ models coefficients and check of their adequacies.
Coeff. EN 1.4462 EN 1.4410
Dry Wet Dry Wet
λ1 4618.4 654.091 4473.3 2369.6
λ2 0.29156 0.49853 0.50425 0.40716
λ3 −1.335 −0.15483 −1.236 −0.8276
  
Check of models adequacy
R2 0.908 0.947 0.904 0.957
0.888 0.936 0.882 0.948
F-value 1.17E + 02 4.55E + 02 1.10E + 02 3.15E + 02
P value 1.56E − 07 3.84E − 10 2.04E − 07 1.98E − 09
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
The width of maximum flank wear (VBmax⁡).
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Progression of the maximum chip temperature and tool wear pattern with cutting time in dry cutting of DSSs.
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Variation of cutting forces with respect to the cutting time.
Details are in the caption following the image
Figure 9 (a)
Open in figure viewerPowerPoint
Wear patterns observed on the flank and rake face of cutting tools under dry and wet machining of DSSs.
Details are in the caption following the image
Figure 9 (b)
Open in figure viewerPowerPoint
Wear patterns observed on the flank and rake face of cutting tools under dry and wet machining of DSSs.
Details are in the caption following the image
Figure 9 (c)
Open in figure viewerPowerPoint
Wear patterns observed on the flank and rake face of cutting tools under dry and wet machining of DSSs.
Details are in the caption following the image
Figure 9 (d)
Open in figure viewerPowerPoint
Wear patterns observed on the flank and rake face of cutting tools under dry and wet machining of DSSs.
Details are in the caption following the image
Figure 9 (e)
Open in figure viewerPowerPoint
Wear patterns observed on the flank and rake face of cutting tools under dry and wet machining of DSSs.
Details are in the caption following the image
Figure 10 (a)
Open in figure viewerPowerPoint
Entanglement of chips around the cutting tool and workpiece at vc = 100 m/min and f = 0.15 mm/rev: (a) EN 1.4462, (b) EN 1.4410.
Details are in the caption following the image
Figure 10 (b)
Open in figure viewerPowerPoint
Entanglement of chips around the cutting tool and workpiece at vc = 100 m/min and f = 0.15 mm/rev: (a) EN 1.4462, (b) EN 1.4410.

5. Multiobjective Optimization of Turning DSSs

The objective of the present study is to simultaneously minimize the resultant cutting force, the specific effective cutting power, and the width of maximum flank wear. The mathematical formulation of the current optimization problem can be stated as follows:
()
subjected to the following constraints:
  • (1)

    arithmetic average roughness (Ra)

    ()

  •  

    where rε is the tool nose radius (rε = 0.8 mm);

  • (2)

    cutting parameters lower and upper bounds:

    ()

The proposed MOBA is implemented in Matlab. The computing time was less than a minute, depending on the iteration number and population size. It was found that the best population size (n), loudness reduction (α), and pulse reduction rate (γ) were 40, 0.8, and 0.8, respectively. Optimization results have shown that MOBA is very efficient and consistently converges to the sets of optimal solutions. Figure 11 shows the Pareto optimal frontier points for different process conditions, at which the designers can determine the final solutions depending on their preferences. The final optimum vc and f and their corresponding R, Ps, and VBmax⁡ are shown in Table 7. These process parameters are the Pareto optimal process parameters that should be shown to the decision maker to simultaneously achieve the desired objectives in turning of the DSSs.
Table 7. Optimal solutions obtained by MOBA.
EN 1.4462 EN 1.4410
Dry Wet Dry Wet
vc f R Ps VBmax⁡ vc f R Ps VBmax⁡ vc f R Ps VBmax⁡ vc f R Ps VBmax⁡
(m/min) (mm/rev) (N) (J/mm3) (µm) (m/min) (mm/rev) (N) (J/mm3) (µm) (m/min) (mm/rev) (N) (J/mm3) (µm) (m/min) (mm/rev) (N) (J/mm3) (µm)
100.000 0.150 555.092 6.240 55.038 100.002 0.150 552.772 5.745 73.142 100.000 0.150 707.119 9.297 64.323 100.000 0.150 723.222 6.591 73.943
180.000 0.150 459.186 4.399 65.327 178.925 0.150 457.782 3.980 97.786 180.000 0.150 588.395 5.001 86.423 180.000 0.150 590.268 5.074 93.937
179.809 0.227 640.756 4.174 171.766 100.002 0.150 552.772 5.745 73.142 142.126 0.150 633.924 6.414 76.894 180.000 0.227 793.979 4.371 200.299
118.334 0.150 526.421 5.644 58.024 179.999 0.227 631.188 3.706 158.178 179.642 0.227 815.592 4.209 218.033 109.167 0.151 706.220 6.318 77.919
100.000 0.150 555.092 6.240 55.038 179.842 0.163 487.654 3.913 107.908 118.837 0.150 670.395 7.747 70.277 115.621 0.151 690.684 6.165 79.277
179.729 0.212 606.666 4.212 146.460 111.331 0.151 535.995 5.364 77.620 179.329 0.166 638.255 4.810 108.341 134.366 0.150 654.234 5.773 83.786
170.492 0.150 467.298 4.543 64.301 179.874 0.227 631.330 3.708 158.123 179.568 0.226 813.246 4.218 216.130 100.000 0.150 723.222 6.591 73.943
179.832 0.169 504.905 4.335 85.972 179.672 0.175 515.706 3.871 117.106 179.173 0.221 800.248 4.266 205.824 179.955 0.213 759.780 4.469 178.940
157.628 0.150 480.225 4.759 63.208 179.251 0.218 612.239 3.741 150.590 179.268 0.207 757.641 4.390 176.307 179.747 0.191 702.116 4.654 146.053
179.888 0.205 590.144 4.228 135.316 165.634 0.151 471.164 4.175 94.621 151.814 0.150 620.582 5.985 79.337 179.967 0.159 616.636 4.964 105.004
179.839 0.156 473.085 4.326 71.161 178.925 0.154 467.061 3.963 100.732 179.280 0.202 745.058 4.429 168.127 131.197 0.151 660.861 5.830 83.364
101.749 0.151 553.565 6.174 55.776 132.912 0.153 512.025 4.785 86.274 135.041 0.151 645.543 6.762 75.408 178.007 0.199 725.385 4.606 156.756
114.216 0.150 532.589 5.764 57.465 102.988 0.150 547.537 5.639 74.226 173.716 0.150 595.388 5.190 85.064 180.000 0.158 613.579 4.976 103.704
179.929 0.176 523.372 4.309 95.492 179.916 0.220 616.011 3.726 152.516 159.154 0.150 611.486 5.694 81.241 124.713 0.150 671.418 5.968 81.315
179.923 0.215 612.819 4.202 151.017 179.477 0.198 568.806 3.795 135.229 114.730 0.150 677.709 8.040 69.017 179.931 0.223 783.550 4.401 193.553
145.718 0.151 493.871 4.984 62.257 172.328 0.151 465.442 4.071 96.599 179.226 0.192 714.582 4.531 149.243 179.955 0.221 779.580 4.412 191.091
179.907 0.227 640.697 4.173 171.836 114.327 0.152 533.722 5.270 79.164 179.368 0.214 779.816 4.320 191.524 179.893 0.218 771.685 4.435 186.105
179.808 0.199 577.399 4.244 126.930 179.547 0.159 479.353 3.932 105.034 179.642 0.227 815.592 4.209 218.033 179.976 0.207 743.816 4.517 169.519
134.048 0.151 506.443 5.240 60.444 179.453 0.195 561.494 3.806 132.648 179.632 0.158 613.573 4.902 97.078 179.966 0.194 709.180 4.627 150.071
179.903 0.152 463.419 4.394 67.048 178.956 0.172 508.174 3.893 114.138 179.835 0.172 656.062 4.723 117.616 179.498 0.201 729.354 4.569 160.676
179.768 0.211 603.537 4.215 144.314 153.385 0.152 486.718 4.375 92.087 127.549 0.150 656.158 7.187 72.956 179.544 0.225 788.856 4.392 196.372
123.923 0.150 518.011 5.493 58.604 139.497 0.152 500.678 4.648 87.505 131.156 0.150 650.430 6.979 73.975 178.354 0.216 769.510 4.465 182.732
128.672 0.151 514.614 5.366 60.214 179.737 0.184 535.372 3.840 123.815 178.196 0.199 738.674 4.482 162.685 179.794 0.199 722.278 4.587 157.058
179.729 0.196 570.192 4.254 122.316 179.272 0.151 459.954 3.970 98.660 178.573 0.188 704.297 4.586 142.492 179.070 0.212 757.201 4.491 176.267
179.925 0.204 588.777 4.229 134.442 130.574 0.151 510.221 4.849 84.347 178.995 0.204 749.654 4.423 170.712 155.898 0.150 620.335 5.409 88.596
109.829 0.150 538.550 5.902 56.563 122.953 0.152 521.943 5.033 82.244 109.399 0.150 687.638 8.456 67.322 118.672 0.151 684.428 6.095 80.102
179.924 0.188 551.210 4.274 111.005 179.727 0.209 592.598 3.759 143.873 179.112 0.182 687.429 4.629 133.563 175.593 0.169 649.518 4.910 116.157
179.444 0.172 512.779 4.331 89.687 174.712 0.151 462.912 4.037 97.120 154.531 0.150 617.407 5.873 80.142 180.000 0.153 597.737 5.042 97.002
179.933 0.202 582.598 4.236 130.391 178.781 0.192 556.182 3.823 130.316 100.000 0.150 707.119 9.297 64.323 179.989 0.173 652.387 4.825 121.279
179.551 0.198 574.023 4.252 124.567 179.838 0.202 575.613 3.780 137.899 179.742 0.218 789.326 4.281 198.813 167.869 0.150 604.674 5.234 91.306
179.810 0.220 625.221 4.191 159.945 179.481 0.167 496.658 3.904 110.650 106.371 0.151 695.876 8.695 66.973 104.371 0.150 713.438 6.462 75.467
179.920 0.163 491.388 4.353 79.502 179.821 0.179 524.095 3.855 120.031 178.411 0.179 678.856 4.683 128.181 179.955 0.206 739.773 4.530 167.150
179.923 0.215 613.379 4.202 151.418 114.521 0.150 529.447 5.273 78.358 179.461 0.209 765.346 4.360 181.724 180.000 0.163 627.234 4.921 109.701
179.954 0.187 548.298 4.277 109.332 179.889 0.214 603.031 3.743 147.766 179.298 0.190 709.018 4.547 146.046 179.722 0.188 694.634 4.679 142.086
Details are in the caption following the image
Figure 11
Open in figure viewerPowerPoint
Pareto front points.

6. Conclusions

An experimental investigation on cutting of EN 1.4462 and EN 1.4410 duplex stainless steels was presented. A modelling technique based on the modified Kienzle’s equation was adopted to model the performances and ANOVA tests were performed to check the models adequacies. With the aid of three-dimensional surface plots, the effects of workpiece materials, process, and cutting conditions on the different cutting performances have been analysed and proper conclusion points have been drawn. Results of the early stages of this study have shown that the values of no-beneficial performances when cutting EN 1.4410 were generally higher than those of cutting EN 1.4462, and in comparison to the dry cutting, wet cutting has shown a general improvement in the machining performance.

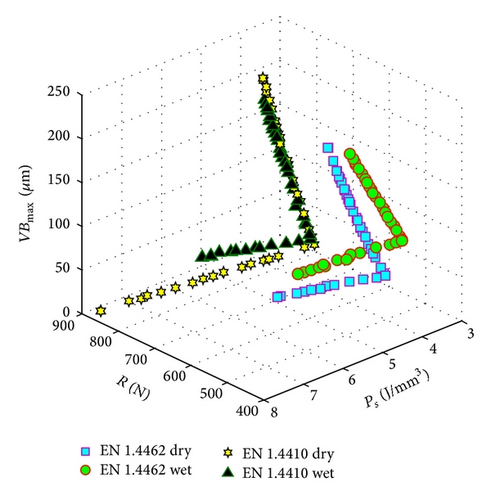
This paper also presented multiobjective optimization of machining duplex stainless steels based on the nature-inspired metaheuristic bat algorithm (MOBA). Three objectives are minimized simultaneously: resultant cutting force, specific effective cutting power, and maximum flank wear. Arithmetic average roughness has been included in the formulation of the optimization problem as a constraint. Results of optimization have shown that MOBA is very efficient and consistently converges to the sets of optimal solutions. It has provided Pareto frontiers of nondominated solution sets for optimum cutting conditions, providing decision makers with a resourceful and efficient means of achieving it. In addition to Pareto’s front graph, the paper is complemented with numerical outcomes.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.