Vibrational spectra of tellurophene and of its perdeuterated isotopomer were computed using the DFT-B3LYP functional with the LANL2DZ(d,p) basis set. The frequencies of fundamental and overtone transitions were obtained in vacuum under the harmonic approximation and anharmonic second-order perturbation theory (PT2). On the whole the anharmonic corrections reduce the harmonic wavenumber values, in many cases better reproducing the observed fundamental frequencies. The largest anharmonic effects are found for the C–H and C–D stretching vibrations, characterized by relatively high anharmonic coupling constants (up to ca. 120 cm⁻¹). For the C–H/C–D stretches, the harmonic H→D isotopic frequency red-shifts overestimate the observed data by 47–63 cm⁻¹ (5.9–8.1%), whereas the PT2 computations exhibit significantly better performances, predicting the experimental data within 1–19 cm⁻¹ (0.1–2.4%).

1. Introduction

Tellurophene is a five-membered heterocycle (C₄H₄Te, Figure 1) homologue of the furan molecule. Tellurophene-based compounds have received great attention for the development and fabrication of promising polymeric conductors [1, 2] and nonlinear optical materials [3–8]. The experimental structure of C₄H₄Te is available from microwave measurements [9], whereas the infrared and Raman spectra of C₄H₄Te and of its perdeuterated isotopomer (C₄D₄Te) were recorded in various phases [10–14]. On the theoretical side, the vibrational spectra of C₄H₄Te were previously calculated in vacuum under the harmonic approximation by using Hartree-Fock [7] and Density Functional Theory (DFT) computations [15]. However, as well-known in the literature, the harmonic treatment often overestimates experimental wavenumbers of fundamentals and overtones, in particular, of the highest-energy spectral regions [16]. To partially circumvent this deficiency, harmonic frequencies can be corrected through scaling procedures [17, 18] or direct anharmonic calculations [19–21]. Anharmonic terms are usually calculated by means of variational [19] or perturbative [20, 21] treatments. As established in the literature [22], the perturbative methods are less accurate than the variational ones. Nevertheless, many recent results attest satisfactory performances of the perturbative methodologies, especially for the prediction of anharmonic contributions to fundamentals and overtones of cyclic compounds [22–30].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

B3LYP/LANL2DZ(d,p) geometrical parameters (r_e structure) of tellurophene. The data reported in the round brackets refer to the B3LYP/LANL2DZ(d,p) vibrationally averaged geometry (r_z structure). The data reported in the square brackets refer to the experimental geometry [9].

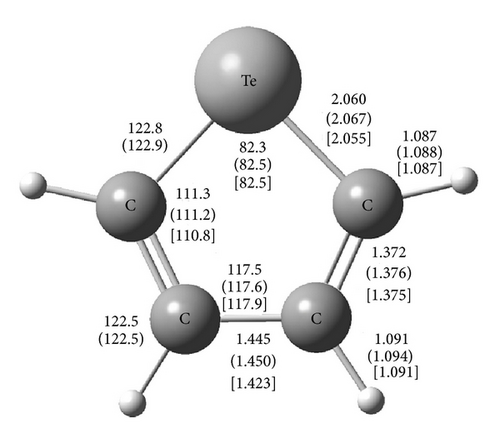
In this work we investigate the effects of the anharmonic corrections on the vibrational wavenumbers of fundamental and overtone transitions of C₄H₄Te and C₄D₄Te. The anharmonic terms were predicted in the gas phase using the second-order perturbation theory (PT2) as described in detail by Barone [20]. The calculations were performed using the hybrid three-parameters B3LYP DFT method [31, 32] with the LANL2DZ(d,p) basis set [33, 34]. Anharmonic PT2-DFT spectra have been previously reported for the congeners furan [22, 25], thiophene [22], and more recently selenophene [30]. To the best of our knowledge, anharmonic theoretical wavenumbers of fundamental and overtone transitions of tellurophene and its perdeuterated isotopomer have been computed here for the first time.

2. Computational Details

The current computations were exclusively performed with the GAUSSIAN 09 package [35]. The structure of C₄H₄Te were fully optimized under the C_2v point group symmetry using the B3LYP functional with the LANL2DZ(d,p) basis set. The vibrational wavenumbers of C₄H₄Te and C₄D₄Te were determined at the B3LYP/LANL2DZ(d,p) level under the harmonic approximation through analytical computations. Anharmonic terms were calculated numerically using the PT2 procedure implemented in the GAUSSIAN 09 program (option: Freq (VibRot, Anharmonic)) [20]. There are many reports in the literature confirming that the PT2 treatment in combination with DFT methods provides satisfactory performances, especially for computing anharmonic vibrational frequencies of cyclic structures [22–30]. In particular, the PT2 method and the B3LYP functional have been employed with success to obtain the vibrational spectra of the homologues furan [22, 25], thiophene [22], and more recently selenophene [30]. The used PT2 scheme computes the third and fourth energy derivatives with respect to the normal coordinates through a numerical differentiation procedure described in detail in [20]. The potential energy surface (V) can be expanded including anharmonic contributions up to the quartic term as

()

where ω_i are the harmonic wavenumbers, q_i are the dimensionless normal coordinates, Φ_ijk and Φ_ijkl, are respectively, the third- and fourth-order force constants. The Φ_ijk and Φ_ijkl values are obtained through a finite difference scheme using quadratic normal coordinate force constants (Φ_ij) calculated analytically and performing displacements along each normal coordinate (

()

As commonly adopted in the literature [24–26, 29, 30], step size displacements of 0.025 Å along the normal coordinates were used in the present work. The fundamental frequencies (ν_i) were determined from the ω_i, diagonal (χ_ii) and off-diagonal (χ_ij) anharmonic constants [20]:

()

3. Result and Discussion

Figure 1 displays the bond lengths and angles of C₄H₄Te calculated at the B3LYP/LANL2DZ(d,p) level. In addition, the figure reports the available experimental data obtained by microwave measurements [9]. The B3LYP/LANL2DZ(d,p) geometry is in good agreement with the observed one, especially for the bond lengths C–Te (within 0.005 Å), C=C (within 0.003 Å), and C–H (the calculated and experimental values are identical), as well as for the bond angles (within 0.2–0.5°). Figure 1 also presents the vibrationally averaged geometries (r_z structure) calculated by the vibration-rotation interaction constant values [20]. In line with previous studies on cyclic compounds [29, 30], the vibrational averaging corrections lengthen the bond lengths of C₄H₄Te by 0.001–0.003 Å, whereas the bond angles vary within 0.2° (C–Te–C).

The experimental infrared and Raman spectra of C₄H₄Te and C₄D₄Te were obtained in vapour, liquid, CCl₄ solution, and solid phase [10–14]. Theoretically, some calculations on the C₄H₄Te isotopomer were previously performed using the harmonic treatment [7, 15]. In Tables 1 and 2 we present the B3LYP/LANL2DZ(d,p) harmonic (ω) and anharmonic wavenumbers (ν), infrared intensities (I_IR) and Raman activities (A_Raman) of C₄H₄Te and C₄D₄Te, together with the available observed data for comparison [12]. The assignments of the vibrations were performed using normal modes as displacements in redundant internal coordinates (in the GAUSSIAN 09, the option: Freq = IntModes) and also through the graphical program Chemcraft [36]. The title compounds belong to the C_2v symmetry point group with the 21 normal modes categorized as 8A₁ + 3A₂ + 7B₁ + 3B₂. All the modes with the exception of the A₂ vibrations are infrared active. It is worth noting that, the current assignments of the transitions reasonably agree with those previously determined by experimental [12] and computational [7, 15] studies. The complete sets of experimental fundamentals of both the investigated isotopomers are available from measurements in liquid phase [12], whereas three C–H stretching transitions (modes numbers 1, 2, and 13) of C₄H₄Te were also detected in gas [11].

Table 1. Vibrational harmonic, ω, and anharmonic, ν, wavenumbers (cm⁻¹), infrared intensities, I_IR (km/mol), and Raman activities A_Raman (Å⁴/amu) of C₄H₄Te.

		Description^a	Calc.^b				Exp.^c
		Description^a	I_IR	A_Raman	ω	ν	ν
A₁	1	νC–H	3	317	3237	3089	3084 (3106)
	2	νC–H	12	259	3191	3052	3045 (3064)
	3	νC=C + νC–C + δC–H	25	54	1465	1430	1432
	4	νring + δC–H	12	3	1341	1311	1316
	5	δC–H	2	5	1103	1083	1079
	6	Ring breathing + δC–H	1	22	1010	986	984
	7	δring	18	22	702	692	687
	8	δC–Te–C	0	9	385	380	380
A₂	9	γC–H	0	1	911	894	912
	10	γC–H	0	0	684	663	690
	11	τring	0	0	512	503	507
B₁	12	νC–H	3	2	3234	3085	3084
	13	νC–H	4	118	3176	3037	3030 (3047)
	14	νC=C + δC–H	3	0	1548	1516	1516
	15	δC–H	31	3	1255	1220	1246
	16	δC–H	0	4	1099	1077	1079
	17	δring	3	0	805	794	797
	18	νC–Te	2	8	557	547	552
B₂	19	γC–H	0	0	876	859	884
	20	γC–H	132	0	683	667	674
	21	τring	5	0	358	355	354
		rms deviation^d			66	11
		rms deviation^e			144	6
		rms deviation^f			21	12

^aν: stretching; δ: in-plane bending; τ: torsion; γ: out-of-plane bending.
^bCalculations were carried out in vacuum at the B3LYP/LANL2DZ(d,p) level.
^cLiquid phase [12]. The values in parentheses refer to the gas phase [11].
^dAll vibrational modes.
^eνC–H modes.
^fAll vibrational modes excluding νC–H modes.

Table 2. Vibrational harmonic, ω, and anharmonic, ν, frequencies (cm⁻¹), infrared intensities, I_IR (km/mol), and Raman activities A_Raman (Å⁴/amu) of C₄D₄Te.

		Description^a	Calc.^b				Exp.^c
		Description^a	I_IR	A_Raman	ω	ν	ν
A₁	1	νC–D	2	143	2400	2294	2308
	2	νC–D	3	104	2355	2270	2262
	3	νC=C + νC–C + δC–D	31	57	1443	1409	1405
	4	νring + δC–D	11	7	1208	1169	1180
	5	δC–D	2	23	839	828	824
	6	Ring breathing + δC–D	0	10	782	770	768
	7	δring	14	12	640	632	630
	8	δC–Te–C	0	9	374	371	370
A₂	9	γC–D	0	1	753	742	741
	10	γC–D	0	0	533	520	548
	11	τring	0	0	438	432	437
B₁	12	νC–D	1	4	2395	2313	2308
	13	νC–D	1	55	2339	2249	2240
	14	νC=C + δC–D	7	0	1493	1458	1455
	15	δC–D	12	2	1002	986	995
	16	δC–D	2	4	853	840	811
	17	δring	1	0	706	697	704
	18	νC–Te	3	7	524	517	522
B₂	19	γC–D	0	0	683	673	696
	20	γC–D	77	0	506	497	502
	21	τring	3	0	329	325	326
		rms deviation^d			43	12
		rms deviation^e			91	10
		rms deviation^f			18	12

^aν: stretching; δ: in-plane bending; τ: torsion; γ: out-of-plane bending.
^bCalculations were carried out in vacuum at the B3LYP/LANL2DZ(d,p) level.
^cLiquid phase [12].
^dAll vibrational modes.
^eνC–H modes.
^fAll vibrational modes excluding νC–H modes.

The harmonic frequencies systematically overestimate the experimental data with the notable exception of the modes numbers 9, 10, and 19 for C₄H₄Te and of the modes numbers 10 and 19 for C₄D₄Te. In the present study, we determined the root mean square (rms) deviation between the experimental and calculated wavenumbers which is defined as follows:

()

where ν_i is a vibrational frequency value. The rms deviations are included in Tables 1 and 2 for all the modes, the C–H/C–D stretching vibrations (νC–H/νC–D), and all the modes except for the νC–H and νC–D vibrations. When considering all the vibrational transitions, the rms deviations between the harmonic and observed data are 66 cm⁻¹ for C₄H₄Te and 43 cm⁻¹ for C₄D₄Te. These rms deviations are noticeably reduced if we exclude the νC–H and νC–D modes, becoming 21 cm⁻¹ and 18 cm⁻¹, respectively. On the whole, the modification of the basis set for the C and H atoms [LANL2DZ(d,p) → 6–311G(d,p)] does not produce significant effects on the harmonic wavenumber values of C₄H₄Te (the data are available on request from the author), giving a rms deviation of 63 cm⁻¹ with respect to the experimental data. Specifically, the performances of the 6-311G(d,p) in comparison to the LANL2DZ(d,p) basis set are slightly improved for the C–H stretches (rms deviation of 135 versus 144 cm⁻¹), but worsened for the remaining modes (rms deviation of 23 versus 21 cm⁻¹). Therefore, for the anharmonic computations the use of the smaller LANL2DZ(d,p) basis set for all the atoms can be considered a reasonable choice. Although the experimental wavenumber values of the 21 fundamentals were obtained in liquid phase [12] and the present calculations were performed in vacuum, the introduction of the PT2 anharmonic corrections generally improves the agreement between the observed and computed data; for all the vibrational transitions the rms deviations are 11 cm⁻¹ for C₄H₄Te and 12 cm⁻¹ for C₄D₄Te. As should be expected, the calculated harmonic wavenumbers overestimate the anharmonic figures, the zero-point energy (ZPE) correction, a physicochemical property of fundamental importance for an accurate determination of thermochemical and kinetic parameters, being influenced by the anharmonic corrections. Indeed, when passing from the harmonic to the PT2 anharmonic treatment, the ZPE for C₄H₄Te (C₄D₄Te) decreases from 40.22 (32.30) to 39.72 (31.44) kcal/mol.

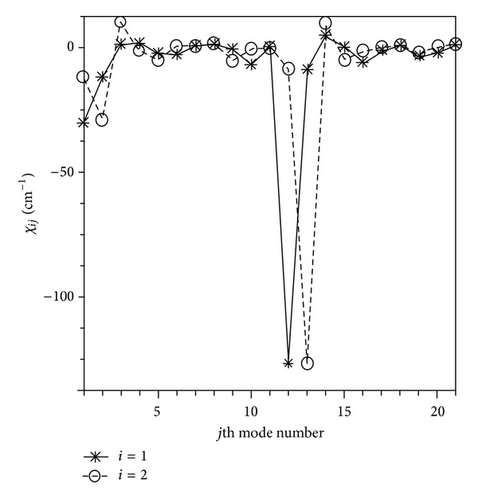
As can be appreciated from the data reported in Tables 1 and 2, the largest anharmonic contributions are found for the νC–H and νC–D transitions (modes. numbers 1, 2, 12, and 13), decreasing the harmonic frequency values of C₄H₄Te by 140–150 cm⁻¹ (ca. 4%) and of C₄D₄Te 80–110 cm⁻¹ (ca. 3-4%), in agreement with previous PT2 computations on other cyclic compounds [22–30]. As a consequence, the agreement between the experimental and calculated wavenumbers for the νC–H and νC–D stretches is significantly improved by the anharmonic treatment (within 1–14 cm⁻¹, 0.03–0.61%). Note that when we consider the gas phase experimental νC–H fundamentals of C₄H₄Te (modes numbers 1, 2, and 13, Table 1), the experimental/calculation deviations are slightly augmented (up to 17 cm⁻¹). To elucidate the origin of the above large anharmonic effects, as a case test, we analysed the contributions of the anharmonic constant values (χ_i,j) for the νC–H modes numbers 1 and 2 of C₄H₄Te (Figure 2). The most significant χ_i,j corrections are produced by the diagonal term (χ_i,i) as well as by the coupling with the remaining C–H stretching modes. In the specific case of the modes numbers 1 and 2, the largest anharmonic coupling are χ_1,12 and χ_2,13, which are predicted to be ca. −120 cm⁻¹ and recover about 80% of the total anharmonic corrections (ω − ν, (3)). Other nonnegligible anharmonic contributions, although less substantial than χ_1,12 and χ_2,13, are given by the χ_1,1, χ_2,2 (ca. −30 cm⁻¹ for both the couplings), and χ_1,2 (−12 cm⁻¹) terms.

For the νC–H/νC–D modes, we evaluated the H→D isotopic wavenumber downward shifts (Δν_H/D = νC–H − νC–D) obtained by the harmonic and anharmonic calculations. The deviations of the calculated Δν_H/D data from the observed values are reported in Figure 3, together with the percentage errors. The harmonic approximation overestimates the experimental shifts by 47–63 cm⁻¹ (5.9–8.1%), whereas the anharmonic computations, with the exception of mode number 1, underestimate the isotopic shifts showing smaller errors (1–19 cm⁻¹, 0.1–2.4%). The results are particularly excellent for the mode number 2.

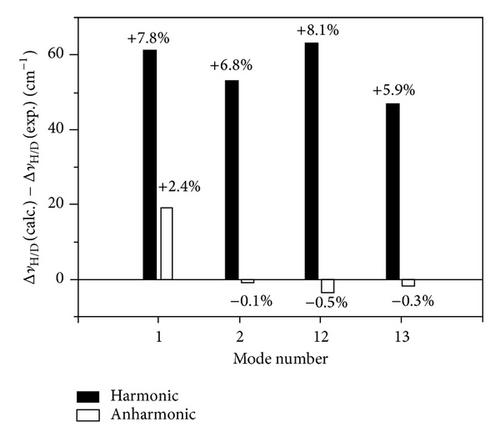
Table 3 collects the frequencies of the overtone bands of title compounds obtained using the harmonic and anharmonic approaches, together with the available experimental data which are only limited to eleven (C₄H₄Te) and five (C₄D₄Te) vibrational modes. Confirming the above results of the fundamentals, the greatest anharmonic corrections for the overtones occur for the νC–H (νC–D) transitions, which reduce the harmonic values by ca. 5-6% (4-5%).

Table 3. Wavenumbers of first overtones (cm⁻¹) of tellurophene isotopomers.

Symm.	Mode no.^a	C₄H₄Te			C₄D₄Te
		Calc.^b		Exp.^c	Calc.^b		Exp.^c
		ω	ν	ν	ω	ν	ν
A₁	1	6474	6144		4801	4575
	2	6382	6047		4711	4516
	3	2931	2848	2851	2886	2810
	4	2683	2617	2627	2415	2343
	5	2205	2167	2160	1678	1652
	6	2019	1968	1966	1563	1541
	7	1404	1382		1279	1263	1254
	8	769	759	758	748	740
A₂	9	1823	1788	1822	1505	1485
	10	1369	1322	1385	1067	1039
	11	1024	1009	1014	877	864	872
B₁	12	6469	6083		4789	4598
	13	6351	6013		4679	4478
	14	3096	3019	3015	2986	2921	2916
	15	2510	2451		2004	1969
	16	2199	2154		1706	1680
	17	1611	1588		1412	1393
	18	1114	1093	1111	1049	1031	1049
B₂	19	1753	1717	1768	1367	1347	1383
	20	1367	1331		1013	993
	21	716	709		657	650

^aSee Tables 1 and 2 for the mode description.
^bCalculations were carried out in vacuum at the B3LYP/LANL2DZ(d,p) level.
^cLiquid phase, [12].

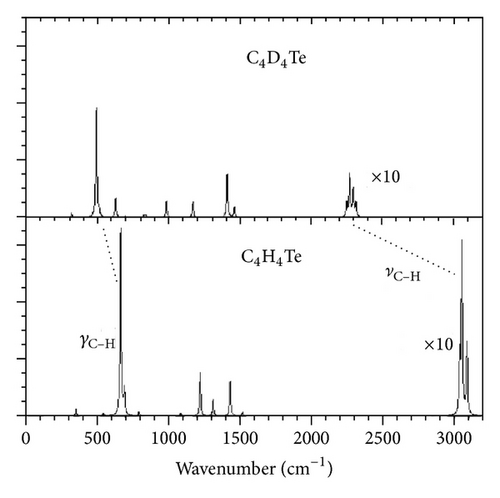
In Figures 4 and 5 we plot the infrared and Raman spectra obtained by the anharmonic calculations using pure Lorentzian band-shapes with a full width at half maximum of 10 cm⁻¹. The C–H and C–D stretching transitions are placed in the highest-wavenumber regions of the vibrations spectra. The lowest-energy region of the infrared spectra of C₄H₄Te and C₄D₄Te is mainly characterized by an isolated and strong absorption located at 667 cm⁻¹ (I_IR = 132 km/mol) and 497 cm⁻¹ (I_IR = 77 km/mol), respectively, to be compared with the experimental values of 674 cm⁻¹ (−1%) and 502 cm⁻¹ (−1%), respectively. The vibrational analysis ascribes this transition (mode number 20) to a pure out-of-plane C–H (and C–D) bending deformation, γC–H (γC–D). A graphical representation of the atomic displacement vectors involved in this vibration is depicted in Figure 6(a).

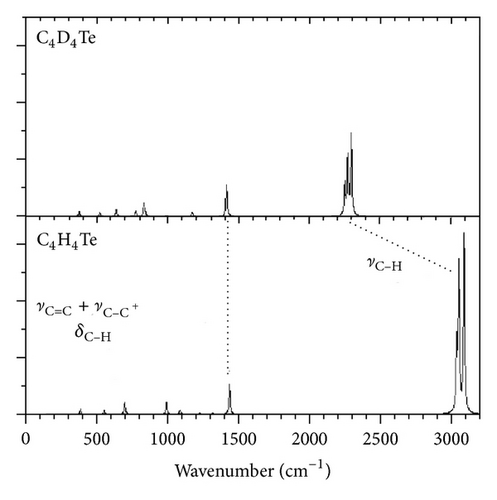
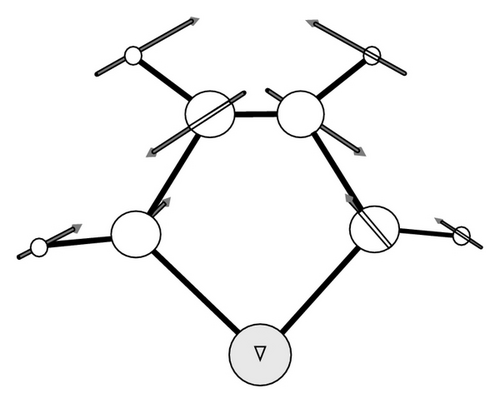
The most active transitions in the Raman spectra of C₄H₄Te and C₄D₄Te involve the C–H and C–D stretches (Tables 1 and 2). From the present calculations, an almost isolated and relatively intense peak (A_Raman ~ 50 Å⁴/amu) located near 1400 cm⁻¹ appears in the Raman spectra of both tellurophene and its perdeuterated isotopomer. This transition (mode number 3) also visible in the infrared spectra is assigned to the C=C + C–C bonds stretchings with the nonnegligible contribution from the in-plane C–H (C–D) bending motion (Figure 6(b)). The present harmonic computations place this band at 1465 cm⁻¹ (C₄H₄Te) and 1443 cm⁻¹ (C₄D₄Te), overestimating the observed wavenumbers of 1432 cm⁻¹ (+2.3%) and 1405 cm⁻¹ (+2.7%), respectively. Note that the corresponding PT2 anharmonic frequencies here calculated at 1430 cm⁻¹ (C₄H₄Te) and 1409 cm⁻¹ (C₄D₄Te), give a noticeably better agreement with experiment (within 0.1–0.3%).

4. Conclusions

In this work we computed harmonic and PT2 anharmonic vibrational frequencies of fundamentals and overtone bands of C₄H₄Te and C₄D₄Te. The computations were performed in vacuum at the B3LYP/LANL2DZ(d,p) level of theory. The infrared and Raman spectral profiles were simulated using Lorentzian band-shapes and the most informative transitions were discussed. In general, the calculated harmonic frequencies deviate from the observed ones, with rms deviations of 66 and 43 cm⁻¹ for C₄H₄Te and C₄D₄Te, respectively. The introduction of the PT2 anharmonic contributions in several cases significantly reduces the calculation/experiment discrepancy, giving rms deviations of 11 cm⁻¹ (C₄H₄Te) and 12 cm⁻¹ (C₄D₄Te). A vibrational analysis reveals that the anharmonic corrections are especially conspicuous for the νC–H and νC–D transitions, decreasing the harmonic wavenumber values, respectively, by 140–150 cm⁻¹ (ca. 4%) and 80–110 cm⁻¹ (ca. 3-4%), and noticeably improving the agreement with the experimental data. As a consequence, in comparison to the harmonic approximation, the observed H→D isotopic frequency red-shifts for the C–H and C–D stretches are better reproduced by the PT2 scheme with deviation up to 1–19 cm⁻¹ (0.1–2.4%). Important anharmonic effects (ca. 35 cm⁻¹, 2.3%) are also found for the mode number 3 (νC=C + νC–C + δC–H, νC=C + νC–C + δC–D), characterized by a relatively intense peak in the Raman spectra. In line with the recent literature, the present results on tellurophene isotopomers confirm that the anharmonic PT2-DFT approach can be employed to accurately predict the infrared and Raman spectra of heterocyclic compounds.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

References

1 Inoue S., Jigami T., Nozoe H., Otsubo T., and Ogura F., 2,2^′-Bitellurophene and 2,2^′:5^′,2^″-tertellurophene as novel high homologues of tellurophene, Tetrahedron Letters. (1994) 35, no. 43, 8009–8012, 2-s2.0-0027973735, https://doi.org/10.1016/0040-4039(94)80035-9.
10.1016/0040-4039(94)80035-9
CAS Web of Science® Google Scholar
2 Lei Q., Yin X. H., Kobayashi K., Kawai T., Ozaki M., and Yoshino K., Electrical properties of polymer composties: conducting polymer-polyacene quinone radical polymer, Synthetic Metals. (1995) 69, no. 1–3, 357–358, 2-s2.0-0029274540.
10.1016/0379-6779(94)02484-G
CAS Web of Science® Google Scholar
3 Millefiori S. and Alparone A., (Hyper)polarizability of chalcogenophenes C₄H₄X (X = O, S, Se, Te) conventional ab initio and density functional theory study, Journal of Molecular Structure: THEOCHEM. (1998) 431, no. 1-2, 59–78, 2-s2.0-0002074771.
10.1016/S0166-1280(97)00418-1
CAS Web of Science® Google Scholar
4 Kamada K., Sugino T., Ueda M., Tawa K., Shimizu Y., and Ohta K., Femtosecond optical Kerr study of heavy-atom effects on the third-order optical non-linearity of thiophene homologues: electronic hyperpolarizability of tellurophene, Chemical Physics Letters. (1999) 302, no. 5-6, 615–620, 2-s2.0-0000809550.
10.1016/S0009-2614(99)00157-8
CAS Web of Science® Google Scholar
5 Millefiori S. and Alparone A., Second hyperpolarisability of furan homologues C₄H₄X (X=O, S, Se, Te): Ab initio HF and DFT study, Chemical Physics Letters. (2000) 332, no. 1-2, 175–180, 2-s2.0-0001171180.
10.1016/S0009-2614(00)01197-0
CAS Web of Science® Google Scholar
6 Kamada K., Ueda M., Nagao H., Tawa K., Sugino T., Shmizu Y., and Ohta K., Molecular design for organic nonlinear optics: polarizability and hyperpolarizabilities of furan homologues investigated by ab initio molecular orbital method, Journal of Physical Chemistry A. (2000) 104, no. 20, 4723–4734, 2-s2.0-0033741386, https://doi.org/10.1021/jp993806y.
10.1021/jp993806y
CAS Web of Science® Google Scholar
7 Millefiori S. and Alparone A., Theoretical determination of the vibrational and electronic (hyper)polarizabilities of C₄H₄X (X = O, S, Se, Te) heterocycles, Physical Chemistry Chemical Physics. (2000) 2, no. 11, 2495–2501, 2-s2.0-0034214167, https://doi.org/10.1039/b001020k.
10.1039/b001020k
CAS Web of Science® Google Scholar
8 Jansik B., Schimmelpfennig B., Norman P., Macak P., Ågren H., and Ohta K., Relativistic effects on linear and non-linear polarizabilities of the furan homologues, Journal of Molecular Structure: THEOCHEM. (2003) 633, no. 2-3, 237–246, 2-s2.0-0042470615, https://doi.org/10.1016/S0166-1280(03)00278-1.
10.1016/S0166-1280(03)00278-1
CAS Web of Science® Google Scholar
9 Yadav V. K., Yadav A., and Poirier R. A., Some periodic trends in organic compounds containing O, S, Se, and Te: an ab initio study, Journal of Molecular Structure: THEOCHEM. (1989) 186, no. C, 101–116, 2-s2.0-33751069637.
10.1016/0166-1280(89)87042-3
Google Scholar
10 Poletti A., Cataliotti R., and Paliani G., Infrared crystal spectra of heterocyclic compounds. II. IR spectrum of selenophene in the solid state, Chemical Physics. (1974) 5, no. 2, 291–297, 2-s2.0-0010425596.
10.1016/0301-0104(74)80027-3
CAS Web of Science® Google Scholar
11 Cataliotti R. and Paliani G., Infrared study of the C-H stretching region of five-membered heterocyclic compounds, Canadian Journal of Chemistry. (1976) 54, 2451–2457.
10.1139/v76-348
CAS Web of Science® Google Scholar
12 Paliani G., Cataliotti R., Poletti A., Fringuelli F., Taticchi A., and Giorgini M. G., Vibrational analysis of tellurophene and its deuterated derivatives, Spectrochimica Acta Part A. (1976) 32, no. 5, 1089–1104, 2-s2.0-4243271955.
10.1016/0584-8539(76)80294-2
Web of Science® Google Scholar
13 Santucci A., Paliani G., and Cataliotti R. S., Force field calculation of the in-plane fundamental motions of tellurophene and selenophene, Spectrochimica Acta Part A. (1985) 41, no. 5, 679–685, 2-s2.0-4243272231.
10.1016/0584-8539(85)80174-4
Web of Science® Google Scholar
14 Santucci A., Paliani G., and Cataliotti R. S., Force field calculation of the out-of-plane fundamental modes of tellurophene and selenophene, Chemical Physics Letters. (1987) 138, no. 2-3, 244–249, 2-s2.0-4243992435.
10.1016/0009-2614(87)80375-5
CAS Web of Science® Google Scholar
15 El-Azhary A. A. and Al-Kahtani A. A., Force field scale factors of effective core potential basis sets of some selenium and tellurium heterocyclic molecules, selenophene, 1,2,5-selenadiazole, tellurophene and 1,2,5-telluradiazole, Journal of Molecular Structure: THEOCHEM. (2001) 572, 81–87, 2-s2.0-0035903849, https://doi.org/10.1016/S0166-1280(01)00556-5.
10.1016/S0166-1280(01)00556-5
CAS Web of Science® Google Scholar
16 Hehre W. J., Random L., Schleyer P. V. R., and Pople J. A., Ab Initio Molecular Orbital Theory, 1986, Wiley, New York, NY, USA.
10.1021/ja00267a063
CAS Google Scholar
17 Pulay P., Fogarasi G., Pongor G., Boggs J. E., and Vargha A., Combination of theoretical ab initio and experimental information to obtain reliable harmonic force constants. Scaled quantum mechanical (SQM) force fields for glyoxal, acrolein, butadiene, formaldehyde, and ethylene, Journal of the American Chemical Society. (1983) 105, no. 24, 7037–7047, 2-s2.0-0020843873.
10.1021/ja00362a005
CAS Web of Science® Google Scholar
18 Rauhut G. and Pulay P., Transferable scaling factors for density functional derived vibrational force fields, Journal of Physical Chemistry. (1995) 99, no. 10, 3093–3100, 2-s2.0-9344269016.
10.1021/j100010a019
CAS Web of Science® Google Scholar
19 Bowman J. M., Self-consistent field energies and wavefunctions for coupled oscillators, The Journal of Chemical Physics. (1978) 68, no. 2, 608–610, 2-s2.0-36749105013.
10.1063/1.435782
CAS Web of Science® Google Scholar
20 Barone V., Anharmonic vibrational properties by a fully automated second-order perturbative approach, Journal of Chemical Physics. (2005) 122, no. 1, 2-s2.0-22944477761, https://doi.org/10.1063/1.1824881, 014108.
10.1063/1.1824881
CAS PubMed Web of Science® Google Scholar
21 ClaboD. A.Jr., Allen W. D., Remington R. B., Yamaguchi Y., and SchaeferH. F.III, A systematic study of molecular vibrational anharmonicity and vibration-rotation interaction by self-consistent-field higher-derivative methods. Asymmetric top molecules, Chemical Physics. (1988) 123, no. 2, 187–239, 2-s2.0-0000761742.
10.1016/0301-0104(88)87271-9
CAS Web of Science® Google Scholar
22 Burcl R., Handy N. C., and Carter S., Vibrational spectra of furan, pyrrole, and thiophene from a density functional theory anharmonic force field, Spectrochimica Acta Part A. (2003) 59, no. 8, 1881–1893, 2-s2.0-0037542453, https://doi.org/10.1016/S1386-1425(02)00421-3.
10.1016/S1386-1425(02)00421-3
CAS PubMed Web of Science® Google Scholar
23 Handy N. C. and Willetts A., Anharmonic constants for benzene, Spectrochimica Acta Part A. (1997) 53, no. 8, 1169–1177, 2-s2.0-14644443483.
10.1016/S1386-1425(96)01864-1
Web of Science® Google Scholar
24 Barone V., Accurate vibrational spectra of large molecules by density functional computations beyond the harmonic approximation: the case of azabenzenes, Journal of Physical Chemistry A. (2004) 108, no. 18, 4146–4150, 2-s2.0-2442660362, https://doi.org/10.1021/jp0497662.
10.1021/jp0497662
CAS Web of Science® Google Scholar
25 Barone V., Vibrational spectra of large molecules by density functional computations beyond the harmonic approximation: the case of pyrrole and furan, Chemical Physics Letters. (2004) 383, no. 5-6, 528–532, 2-s2.0-0347753690, https://doi.org/10.1016/j.cplett.2003.11.066.
10.1016/j.cplett.2003.11.066
CAS Web of Science® Google Scholar
26 Barone V., Festa G., Grandi A., Rega N., and Sanna N., Accurate vibrational spectra of large molecules by density functional computations beyond the harmonic approximation: the case of uracil and 2-thiouracil, Chemical Physics Letters. (2004) 388, no. 4-6, 279–283, 2-s2.0-1842688206, https://doi.org/10.1016/j.cplett.2004.03.024.
10.1016/j.cplett.2004.03.024
CAS Web of Science® Google Scholar
27 Boese A. D. and Martin J. M. L., Vibrational spectra of the azabenzenes revisited: anharmonic force fields, Journal of Physical Chemistry A. (2004) 108, no. 15, 3085–3096, 2-s2.0-2342614934, https://doi.org/10.1021/jp0369589.
10.1021/jp0369589
CAS Web of Science® Google Scholar
28 Librando V., Alparone A., and Minniti Z., Computational note on anharmonic infrared spectrum of naphthalene, Journal of Molecular Structure: THEOCHEM. (2007) 847, no. 1-3, 23–24, 2-s2.0-36048936994, https://doi.org/10.1016/j.theochem.2007.08.022.
10.1016/j.theochem.2007.08.022
CAS Web of Science® Google Scholar
29 Alparone A., Ab initio and DFT anharmonic spectroscopic investigation of 1,3-cyclopentadiene, Chemical Physics. (2006) 327, 127–136.
10.1016/j.chemphys.2006.04.004
CAS Web of Science® Google Scholar
30 Alparone A., Infrared and Raman spectra of C₄H₄Se and C₄D₄Se isotopomers: a DFT-PT2 anharmonic study, Journal of Chemistry. (2013) 2013, 8, https://doi.org/10.1155/2013/741472, 741472.
10.1155/2013/741472
Web of Science® Google Scholar
31 Becke A. D., A new mixing of Hartree-Fock and local density-functional theories, The Journal of Chemical Physics. (1993) 98, no. 2, 1372–1377, 2-s2.0-34250817103.
10.1063/1.464304
CAS Web of Science® Google Scholar
32 Lee C., Yang W., and Parr R. G., Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Physical Review B. (1988) 37, no. 2, 785–789, 2-s2.0-0345491105, https://doi.org/10.1103/PhysRevB.37.785.
10.1103/PhysRevB.37.785
CAS PubMed Web of Science® Google Scholar
33 DunningT. H.Jr. and Hay P. J., H. F. Schaefer, Modern Theoretical Chemistry, 1976, 3, Plenum, New York, NY, USA, 1–28.
Google Scholar
34 Wadt W. R. and Hay P. J., Ab initio effective core potentials for molecular calculations. Potentials for main group elements Na to Bi, The Journal of Chemical Physics. (1985) 82, no. 1, 284–298, 2-s2.0-0006073669.
10.1063/1.448800
CAS Web of Science® Google Scholar
35 Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Mennucci B., Petersson G. A., Nakatsuji H., Caricato M., Li X., Hratchian H. P., Izmaylov A. F., Bloino J., Zheng G., Sonnenberg J. L., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Montgomery J. J. A., Peralta J. E., Ogliaro F., Bearpark M., Heyd J. J., Brothers E., Kudin K. N., Staroverov V. N., Kobayashi R., Normand J., Raghavachari K., Rendell A., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Rega N., Millam J. M., Klene M., Knox J. E., Cross J. B., Bakken V., Adamo C., Jaramillo J., Gomperts R., Stratmann R. E., Yazyev O., Austin A. J., Cammi R., Pomelli C., Ochterski J. W., Martin R. L., Morokuma K., Zakrzewski V. G., Voth G. A., Salvador P., Dannenberg J. J., Dapprich S., Daniels A. D., Farkas O., Foresman J. B., Ortiz J. V., Cioslowski J., and Fox D. J., GAUSSIAN 09, Revision A.02, 2009, Gaussian, Inc., Wallingford, Conn, USA.
Google Scholar
36 Zhurko G. A. and Zhurko D. A., Chemcraft, http://www.chemcraftprog.com/.
Google Scholar

All articles

Anharmonic Spectroscopic Investigation of Tellurophene and Its Perdeuterated Isotopomer: Application of Second-Order Perturbation Theory

Abstract

1. Introduction

2. Computational Details

3. Result and Discussion

4. Conclusions

Conflict of Interests

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Anharmonic Spectroscopic Investigation of Tellurophene and Its Perdeuterated Isotopomer: Application of Second-Order Perturbation Theory

Abstract

1. Introduction

2. Computational Details

3. Result and Discussion

4. Conclusions

Conflict of Interests

References

Figures

References

Related

Information