International Journal of Manufacturing Engineering
Volume 2014, Issue 1 804705
Research Article
Open Access

Studies on the Process Parameters of Rapid Prototyping Technique (Stereolithography) for the Betterment of Part Quality

Raju Bangalore Singe Gowda, 

Corresponding Author

Raju Bangalore Singe Gowda

Department of Mechanical Engineering, REVA ITM, Bangalore, Karnataka 560037, India revainstitution.org

Search for more papers by this author
Chandra Sekhar Udayagiri, 

Chandra Sekhar Udayagiri

Institution of Engineers (India), Gachibowli, Hyderabad 500032, India ieindia.org

Search for more papers by this author
Drakshayani Doulat Narendra, 

Drakshayani Doulat Narendra

Department of Mechanical Engineering, Sir MVIT, Bangalore, Karnataka 562157, India sirmvit.edu

Search for more papers by this author
First published: 11 December 2014
https://doi.org/10.1155/2014/804705
Citations: 12
Academic Editor: Konstantinos Salonitis

Abstract

Rapid prototyping (RP) has evolved as frontier technology in the recent times, which allows direct transformation of CAD files into functional prototypes where it tremendously reduces the lead time to produce physical prototypes necessary for design verification, fit, and functional analysis by generating the prototypes directly from the CAD data. Part quality in the rapid prototyping process is a function of build parameters such as hatch cure depth, layer thickness, orientation, and hatch spacing. Thus an attempt was made to identify, study, and optimize the process parameters governing the system which are related to part characteristics using Taguchi experimental design techniques quality. The part characteristics can be divided into physical part and mechanical part characteristics. The physical characteristics are surface finish, dimensional accuracy, distortion, layer thickness, hatch cure, and hatch file, whereas mechanical characteristics are flexural strength, ultimate tensile strength, and impact strength. Thus, this paper proposes to characterize the influence of the physical build parameters over the part quality. An L9 orthogonal array was designed with the minimum number of experimental runs with desired parameter settings and also by analysis tools such as ANOVA (analysis of variance). Establishment of experimentally verified correlations between the physical part characteristics and mechanical part characteristics to obtain an optimal process parameter level for betterment of part quality is obtained. The process model obtained by the empirical relation can be used to determine the strength of the prototype for the given set of parameters that shows the dependency of strength, which are essential for designers and RP machine users.

1. Introduction

Due to the advances in electronics and computers, there has been a significant growth in communication, information technology, and worldwide networking, which leads to globalization and opening of markets [1, 2]. Thus in product development, rapid prototyping (RP) and rapid product development have turned out to be the key instruments to save time and money with respect to the development of innovative products [2, 3]. Stereolithography (SLA) is one of the RP techniques, which involve fabrication of intricate shape of a plastic monomer directly from computer aided design (CAD) data by depositing material layer by layer by photopolymerization process [4]. The SLA process involves the following steps: conversion of the CAD model to the standard triangulation language (STL) file format; slicing the STL file into thin cross sectional layers; constructing the model by one layer on top of another layer; cleaning and finishing off the model. SLA prototypes have wide applications in aerospace, automobile, and manufacturing sectors especially in rapid tooling. Strength plays a very important role in rapid tooling [5] where the components have to withstand high pressure during the test of fitment and also when used as a die in injection moulding, where the dies prepared through SLA process will be subjected to high tension due to high injection pressure. Taguchi technique is a powerful tool for the design of high quality systems [6, 7]; it provides a simple efficient and systematic approach to optimize design for performance, quality, and cost. The methodology is valuable when design parameters are qualitative and discrete. Taguchi parameter design can optimize the performance characteristic through the setting of design parameters and reduce the sensitivity of the system performance to source of variation [8]. Dingal et al. used Taguchi method to find out the significant factors influencing density, porosity, and hardness on selective laser sintering of iron powder [9]. Guharaja et al. made an attempt to obtain optimal settings of green sand casting parameters using Taguchi method [10]. Rao and Padmanabhan used Taguchi method and ANOVA in optimization of process parameters for material removal rate in electrochemical machining of Al/5% SiC composites [11]. Nataraj et al. used risk analysis Taguchi method to find optimum conditions of design parameters [12]. Barua et al. used the Taguchi method to optimize the mechanical properties of vacuum casting process [13]. Hence, an attempt is made in order to achieve high strength of the prototypes with the specified process parameters which gives prior information of the part strength before fabricating the actual SLA prototypes. Hence, parameter optimization of SLA process is investigated and evaluated through a standard test specimen [14, 15].

2. The Experimental Methods and Methodology

The experimental building material adopted is CIBATOOL 5530 epoxy resin. The experimental building models are categorized into three specimens, namely, the tensile test (Figure 1), flexural test (Figure 2), and impact test (Figure 3), and are characterized using ASTM D638-01 [16], ASTM D790-03 [17], and ASTM D256-04 [18] specifications, respectively. The STL format is generated by CATIA V5 R16 and sent to the 3D system SLA 5000 rapid prototyping machine. The various conditions in preprocessing steps such as STL verification, deposition layer thickness, orientation, building interior structure form, supporting method, and building deposition direction are incorporated by means of 3D light year software [19] provided by 3D system of Valencia, USA, followed by the layer slicing process to generate the building path with ACES build style. Building quality characteristics or attributes include the-larger-the-better (LB) for the strength of the SLA prototypes.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Tensile test specimen as per ASTM D638-01.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Flexural test specimen as per ASTM D790-03.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Impact test specimen as per ASTM D256-04.

2.1. Experimental Apparatus

The major experimental apparatus adopted includes 3D system SLA5000 rapid prototyping machine produced by the Valencia, USA, where it uses CIBATOOL 5530 epoxy resin to build geometrical shape of the work piece by photopolymerization process. Similarly, the tensile and flexural tests were conducted using Instron Universal Testing Machine, UK, Model 5582. The impact test was conducted using impact tester, Aditya Instruments, Bangalore, Model IT-30.

2.2. Taguchi Quality Engineering

The orthogonal array is employed for the Taguchi method as the experimental analysis basis. The experimental factors and their corresponding levels are identified. Then the experimental results are manipulated and validated by analysis of variance (ANOVA), in order to determine each factor effect versus the response variable strength of the SLA prototypes. The experimental procedures are given as follows: identification of SLA process parameter that influences the response variable and determining the various levels of the factors. Based on the factors and their levels, the degree of freedom is calculated and the suitable orthogonal array is selected and the experiment proceeds according to the variable factor layout of the orthogonal array. The experimental results are obtained and the signal to noise ratio (S/N ratio), the ANOVA, and the corresponding contribution are computed, obtaining the empirical relationship for the response variable under different parameter settings.

In the Taguchi method, parameter design converts the objective value to S/N ratio, which is known as quality characteristic evaluation index [20–22], with the S/N ratio where the least variation and the optimal quality design can be obtained. The S/N ratio is beneficial in increasing factor weighting effect, decreasing mutual action, simultaneously processing the average and variation, and improving the quality. The higher the S/N ratio is, the more stable the quality can be obtained. According to the response variable, the-larger-the-better (LB) is used. In the LB, the objective optimal value is larger better for the strength of the SLA prototypes:
()
where η is S/N ratio; yi is the ith result of the experiment; n is the number of replications.

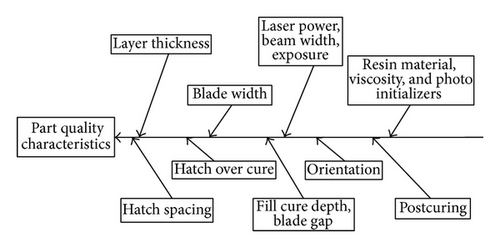
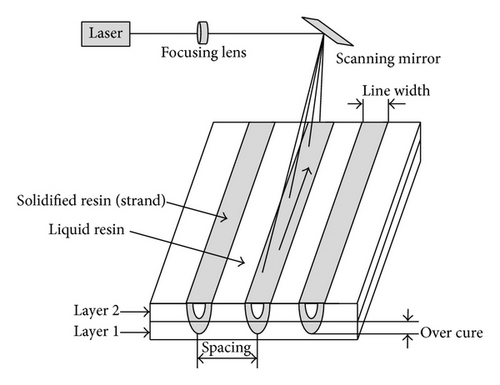
Figure 4 shows the probable parameters (causes) that influence the part quality characteristics (effects) in the SLA process. Figure 5 represents the various process parameters of SLA process, and among these the layer thickness (Lt) is the thickness where the model is sliced in the Z direction, orientation (O) is the position in which the prototype is built, and hatch spacing (Hs) is the narrow region solidified by the laser scanning. If the strand is located at the top or bottom surface of part, spacing is called fill spacing otherwise hatch spacing, which are the parameters that influence the strength of the SLA parts [23]. Table 1 provides the three levels of the process parameters for the experimentation.

Table 1. Description of experimental control parameters.
Symbol Control parameters Level 1 Level 2 Level 3
A Layer thickness (Lt) 0.075 0.1 0.125
B Orientation (O) 0° (Hx) 45° (VHxy) 90° (Vy)
C Hatch spacing (Hs) 0.01 0.015 0.02
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Cause and effect diagram of SLA process parameters.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Process parameter in SLA process.

The total number of experiments in full factorial design for “m” parameters in each set of “L” levels is Lm and it increases exponentially with L & m. Taguchi suggested the use of orthogonal array which will be used for conducting the fractional factorial experiments [24]. The Taguchi orthogonal array adopted in the research experiment is L9 for three-factor three-level settings as shown in Table 2.

Table 2. L9 orthogonal array.
Experimental run (j) Levels
A B C
Layer thickness (Lt)—mm Orientation (O)—° Hatch spacing (Hs)—mm
1 1 1 1
2 1 2 2
3 1 3 3
4 2 1 2
5 2 2 3
6 2 3 1
7 3 1 3
8 3 2 1
9 3 3 2

3. Experimentation

3.1. Experimental Analysis for Tensile Strength (Ts)

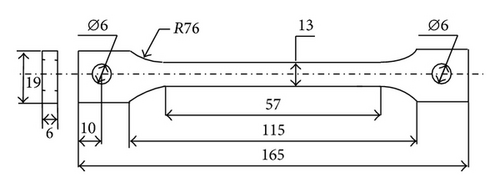
The nine tensile specimens as per the ASTM standards (ASTM D638-01) were built for L9 orthogonal array setting using epoxy resin CIBATOOL SL5530 in SL5000 machine of three replications each. The dimensional details of the test specimen are given in Figure 1 [16] and the SLA prototypes are as shown in Figure 6. The tensile strength is calculated using the ratio of ultimate load to cross sectional area. The experimental results are given in Table 3.

Table 3. Ultimate tensile strength for OA settings.
j 1 2 3 4 5 6 7 8 9
Tsj (N/mm2) 55.46 54.57 55.07 58.46 54.51 58.59 58.62 55.34 61.73
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
SLA prototypes of tensile test specimen.

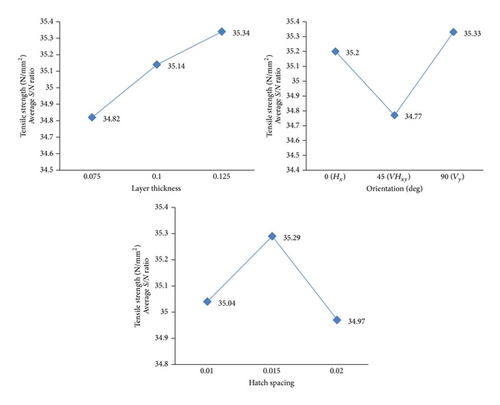
3.1.1. Prediction of Optimal Levels of Process Parameters

S/N ratio is an evaluation measure for the process parameters at each of their process levels where the signal represents the desirable target (LB of tensile strength) and noise indicates the undesirable value which is defined in (1). The average S/N ratio for each process parameter (control variable) at each level is an average of nj at a defined level. Table 4 provides the average S/N ratios for the process parameters (Lt, O, and Hs) at the three levels. The graph represented in Figure 7 shows the variation of average S/N ratio with respect to the various levels. The main objective is to maximize the tensile strength of the parts produced by SLA process; in order to achieve this S/N ratio should be more. Hence, the level having higher S/N ratio is selected as the optimum level, which is contributing higher strength to the part. Therefore, the optimum levels contributing to the higher strength of the part are as follows:
  •  

    layer thickness: 0.125 mm (level 3, S/N ratio: 35.34),

  •  

    orientation: 90°  Vy (level 3, S/N ratio: 35.33),

  •  

    hatch spacing: 0.015 (level 2, S/N ratio: 35.29).

Table 4. S/N ratio for different levels for tensile strength.
Parameters Level Expm run Tsj (N/mm2) nj navg
Layer thickness 1 (0.075) 1 55.46 34.89 34.82
2 54.57 34.74
3 55.07 34.82
2  (0.1) 4 58.46 35.34 35.14
5 54.51 34.73
6 58.59 35.36
3  (0.125) 7 58.62 35.36 35.34
8 55.34 34.86
9 61.73 35.81
  
Orientation 1  (0°) 1 55.56 34.89 35.2
4 58.46 35.34
7 58.62 35.36
2  (45°) 2 54.57 34.74 34.77
5 54.51 34.73
8 55.34 34.86
3  (90°) 3 55.07 34.82 35.33
6 58.59 35.36
9 61.73 35.81
  
Hatch spacing 1  (0.01) 1 55.56 34.89 35.04
6 58.59 35.36
8 55.34 34.86
2  (0.015) 2 54.57 34.74 35.29
4 58.46 35.34
9 61.73 35.81
3  (0.02) 3 55.07 34.82 34.97
5 54.51 34.73
7 58.62 35.36
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
S/N ratio graph for tensile strength analysis.

3.1.2. Identification of Significance and Percentage of Contribution of Process Parameters

The process parameters (Lt, O, and Hs) which have more influence on the response variable are identified through the percentage of contribution of each parameter. The parameter which has more percentage of contribution is the significant parameter to the response variable [25–28]. They have mentioned that ANOVA is widely used for determining the significance of the independent variables in influencing the dependent variables and also in determination of percentage of contribution of these dependent variables to the response variable.

Table 5 shows the percentage of contribution of the parameters to the response variable with the ANOVA parameters. Hence, from the ANOVA table the significance of each parameter is identified.

Table 5. The % of contribution of the parameters to the tensile strength along with the estimated ANOVA parameter.
Parameter “i” Sum of squares Degree of freedom Mean sum of squares F statistics F tabulated % of contribution
F(0.1,2,2)
Lt 18.57 2 9.285 9.622*   36.93
O 21.72 2 10.86 11.25* 9 43.19
Hs 8.06 2 4.03 4.176   16.03
  
Error 1.93 2 0.965     3.83
  
Total 50.28 8 25.14      
  •  *Significance at 90% confidence level (F statistics > F tabulated).

3.2. Experimental Analysis for Flexural Strength (Fs)

The analysis carried out for the flexural strength is identical to the one in Section 3.1. The nine flexural test specimens as per the ASTM standards (ASTM D790-03) were built for L9 orthogonal array setting using epoxy resin CIBATOOL SL5530 in SL5000 machine of three replications each. The dimensional details of the test specimen are given in Figure 2 [17] and the SLA prototypes are as shown in Figure 8. The flexural specimens are subjected to point load at the midpoint between the supports, which are placed at 190 mm apart with a particular load where the fatigue occurs. The flexural strength at fracture (δ) is determined by
()
where W is load in Newton, L is the length of the test specimen in mm, b is the breadth of the test specimen in mm, and d is the thickness of the test specimen in mm. The experimental results are tabulated in Table 6 which shows the flexural strength. Table 7 shows the S/N ratio calculations for each of the levels in each factor which predicts the optimum level among the selected 3 levels and Figure 9 shows the variation of S/N ratio for all the controllable factors.
Table 6. Flexural strength for OA settings.
j exp., run 1 2 3 4 5 6 7 8 9
FSj (N/mm2) 116.67 113.92 114.08 115.7 110.0 115.6 115.8 114.8 118.7
Table 7. S/N ratio for different levels for flexural strength.
Parameters Level Expn run Fsj (N/mm2) nj navg
Layer thickness 1 (0.075) 1 116.67 41.33 41.2
2 113.92 41.13
3 114.08 41.14
2 (0.1) 4 115.7 41.26 41.11
5 110.0 40.82
6 115.6 41.25
3 (0.125) 7 115.8 41.27 41.32
8 114.8 41.20
9 118.7 41.49
  
Orientation 1 (0°) 1 116.67 41.33 41.28
4 115.7 41.26
7 115.8 41.27
2 (45°) 2 113.92 41.13 41.05
5 110.0 40.82
8 114.8 41.20
3 (90°) 3 114.08 41.14 41.30
6 115.6 41.25
9 118.7 41.49
  
Hatch spacing 1 (0.01) 1 116.67 41.33 41.26
6 115.6 41.25
8 114.8 41.20
2 (0.015) 2 113.92 41.13 41.29
4 115.7 41.26
9 118.7 41.49
3 (0.02) 3 114.08 41.14 41.08
5 110.0 40.82
7 115.8 41.27
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
SLA prototypes of flexural test specimen.
Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
S/N ratio graph for flexural strength analysis.
The level which has higher S/N ratio is selected as the optimum level contributing higher flexural strength to the part. Hence the optimal parameters are as follows:
  •  

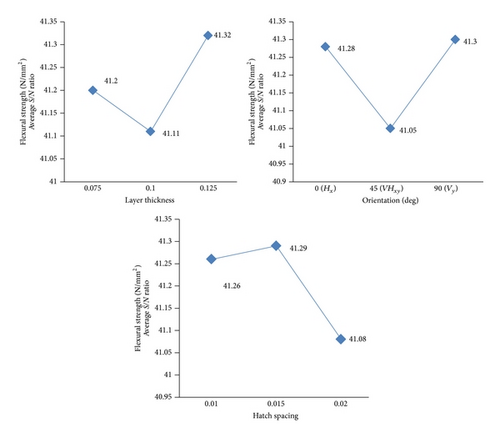
    layer thickness: 0.125 mm (level 3, S/N ratio: 41.32),

  •  

    orientation: 90° Vy (level 3, S/N ratio: 41.3),

  •  

    hatch spacing: 0.015 (level 2, S/N ratio: 41.29).

Table 8 represents the percentage of contribution of each factor for flexural strength along with the estimated ANOVA parameters. From the ANOVA table the significance of each parameter is identified.
Table 8. The % of contribution of the parameters to the flexural strength along with the estimated ANOVA parameter.
Parameter “i” Sum of squares Degree of freedom Mean sum of squares F statistics F tabulated % of contribution
F(0.01,2,2)
Lt 10.75 2 5.375 82.69   23.88
O 20.3 2 10.15 156.15* 99 45.09
Hs 13.84 2 6.92 106.45*   30.75
  
Error 0.13 2 0.065     0.28
  
Total 45.02 8 22.507      
  •  *Significance at 99% confidence level (F statistics > F tabulated).

3.3. Experimental Analysis for Impact Strength

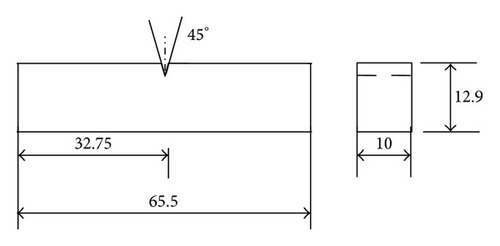
The analysis carried out for the impact strength is identical to the one in Section 3.1. The nine impact test specimens as per the ASTM standards (ASTM D256-04) are built for L9 orthogonal array setting using epoxy resin CIBATOOL SL5530 in SL5000 machine of three replications each. The dimensional details of the test specimen are given in Figure 3 [18] and the SLA prototypes are shown in Figure 10. In Izod test method, the specimen is placed vertically and is broken by a single swing of the pendulum weight with a contact point at a fixed distance from the centerline of the notch. The impact strength is obtained through the ratio of energy absorbed by the specimen during the break and the width of the specimen using Izod impact tests. The experimental results of impact strength are tabulated in Table 9. Table 10 shows the S/N ratio for each of the levels in each factor and Figure 11 shows the variation of S/N ratio for all the controllable factors.

Table 9. Impact strength for OA setting.
j exp., run 1 2 3 4 5 6 7 8 9
ISj (J/m) 20.8 22 21.1 20.3 17.9 21.3 21.4 19.9 23.6
Table 10. S/N ratio for different levels for impact strength.
Parameters Level Experimental run Isj (J/m) nj navg
Layer thickness 1 (0.075) 1 20.8 26.36 26.56
2 22 26.85
3 21.1 26.48
2 (0.1) 4 20.3 26.15 25.93
5 17.9 25.06
6 21.3 26.57
3 (0.125) 7 21.4 26.61 26.68
8 19.9 25.97
9 23.6 27.46
  
Orientation 1 (0°) 1 20.8 26.36 26.37
4 20.3 26.15
7 21.4 26.61
2 (45°) 2 22 26.85 25.96
5 17.9 25.06
8 19.9 25.97
3 (90°) 3 21.1 26.48 26.84
6 21.3 26.57
9 23.6 27.46
  
Hatch spacing 1 (0.01) 1 20.8 26.36 26.3
6 21.3 26.57
8 19.9 25.97
2 (0.015) 2 22 26.85 26.82
4 20.3 26.15
9 23.6 27.46
3 (0.02) 3 21.1 26.48 26.05
5 17.9 25.06
7 21.4 26.61
Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
SLA prototypes of impact test specimen.
Details are in the caption following the image
Figure 11
Open in figure viewerPowerPoint
S/N ratio graph for impact strength analysis.
The level which has higher S/N ratio is selected as the optimum level contributing higher impact strength to the part. Hence the optimal parameters are as follows:
  •  

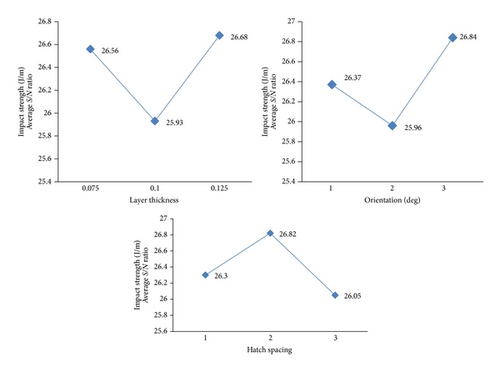
    layer thickness: 0.125 mm (level 3, S/N ratio: 26.68),

  •  

    orientation: 90°  Vy (level 3, S/N ratio: 26.84),

  •  

    hatch spacing: 0.015 (level 2, S/N ratio: 26.82).

Table 11 represents the percentage of contribution of each factor for impact strength along with the estimated ANOVA parameters. From the ANOVA table the significance of each parameter is identified.
Table 11. The % of contribution of the parameters to the impact strength along with the estimated ANOVA parameter.
Parameter “i” Sum of squares Degree of freedom Mean sum of squares F statistics F tabulated % of contribution
F(0.01,2,2)
Lt 5.5 2 2.75 2.69   28.47
O 6.44 2 3.22 3.16* 3 33.33
Hs 5.34 2 2.67 2.617   27.64
  
Error 2.04 2 1.02     10.55
  
Total 19.32 8 9.66      
  •  *Significance at 75% confidence level (F statistics > F tabulated).

4. Establishment of Process Model (Regression Equation)

ANOVA reveals that the layer thickness, orientation, and hatch spacing are contributing significantly to mechanical properties. Hence, establishment of a process model (empirical relationship/regression model) for mechanical properties (tensile/flexural/impact strength) as a function of process parameters (layer thickness, orientation, and hatch spacing) is used to predict the strength for the given set of process parameters, which provides the prior information of the strength before fabricating the SLA prototype and is useful for rapid designers as well as RP machine users. Montgomery [24] suggests the orthogonal polynomial which is very useful for developing the process model with the L9 orthogonal data. A quadratic polynomial model is proposed to establish the process model between the response variable and process parameter as shown in
()
where RV is response variable, i is process parameter identifier, β0 is constant coefficient, β1i is linear coefficient for the ith parameter, β2i is nonlinear coefficient for the ith parameter, ϵ is error component, P1(i) is 1st order orthogonal polynomial of parameter, and P2(i) is 2nd order orthogonal polynomial of the parameter.

4.1. Empirical Relation for Tensile Strength versus Process Parameters

Layer thickness, orientation, and hatch spacing influence the tensile strength and the response variable. The regression equation for the tensile strength is as given by
()
Among the above process parameters, layer thickness and hatch spacing are based on quantitative measures with equal spacing and orientation is based on qualitative measures. Hence the coded value of the orthogonal array is used with two extremes and the center value, that is, lower, higher, and middle values which are coded as −1, 0, and 1, respectively [29, 30]. Table 12 provides the values of orthogonal contrast coefficient for linear and nonlinear terms. Hence, the mean value of the levels of process parameters () becomes zero and the spacing between the levels of process parameters (di) becomes one. Therefore, the study with three parameters will have λ1 = 1 and λ2 = 3 [16]. Substituting the value of , di,  λ1, and λ2, the equation becomes as shown in
()
By using the coded value of the orthogonal contrast coefficients for linear and nonlinear term, the constant and coefficients with respect to the various process parameters are found out and the process model (empirical relation) is given in
()
Table 12. Orthogonal contrast coefficients for linear and nonlinear terms at different levels.
Levels Linear Nonlinear
Lower −1 1
Medium 0 −2
Higher 1 1

4.2. Empirical Relation for Flexural Strength versus Process Parameters

Similarly the process model is established between flexural strength versus process parameter (Lt, O, and Hs) as in Section 4.1 and as given in
()

4.3. Empirical Relation for Impact Strength versus Process Parameters

In a similar manner, the process model is established between impact strength versus process parameter (Lt, O, and Hs) as in Section 4.1 and as given in
()

5. Conclusions

Optimizing the rapid prototyping SLA process by using Taguchi method is proposed. In this paper, an attempt is made to analyze the process parameters that influence the strength aspect of the SLA parts which are useful for various applications of the prototypes in testing and tooling process. The major conclusions are as follows.
  • (i)

    Parameters Lt, O, and Hs influence much on part strength of SLA prototypes.

  • (ii)

    The optimal level combination of the process parameters is as follows:

    •  

      layer thickness: 0.125 mm (level 3),

    •  

      orientation: 90°Vy (level 3),

    •  

      hatch spacing: 0.015 (level 2),

  •  

    for tensile, flexural, and impact strength of the SLA prototypes.

  • (iii)

    Among the three process parameters, the Lt and O are major contributing parameters for the tensile strength, O and Hs are major contributing parameters for the flexural strength, and O has more significance among the parameters for the impact strength.

  • (iv)

    The empirical relationship (process model) between the part strength characteristics and the influencing parameters has been established for stereolithography process, which can predict the strength of the SLA prototypes by prior knowledge of part strength before building the prototypes.

  • (v)

    The layer thickness plays an important role since the SLA process has an inbuilt specific property of building the prototypes with layer by layer method.

The procedure is applied in order to optimize the other rapid prototyping process with different materials. The optimization is done by factorial design (Taguchi technique) to know the effect of parameter on the variables which can be determined by integrating the Taguchi method with grey relational analysis where the optimal parameter combinations of the multiple quality characteristics can be obtained. The process model may be further refined by using nonclassical optimization techniques such as genetic algorithm and neural networks.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

The authors would like to thank the management of Reva Institute of Technology and Management, Bangalore, and the Director of the Gas Turbine Research Establishment, Bangalore, and Sriram Industries, Bangalore, for their immense help to carry out this work.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.