Considering the hypersonic aerospace vehicle, with high dynamic, strong varying parameters, strong nonlinear, strong coupling, and the complicated flight environment, conventional flight control methods based on linear system may become invalid. To the high precision and reliable control problem of this vehicle, nonlinear flight control strategy based on neural network robust adaptive dynamic inversion is proposed. Firstly, considering the nonlinear characteristics of aerodynamic coefficients varying with Mach numbers, attack angle, and sideslip angle, the complete nonlinear 6-DOF model of RBV is established. Secondly, based on the time-scale separation, using the nonlinear dynamic inversion control strategy achieves the pseudolinear decoupling of RBV. And then, using the neural network with single hidden layer approximates the dynamic inversion error for system model uncertainty. Next, the external disturbance and network approximating error are suppressed by robust adaptive control. Finally, using Lyapunov’s theory proves that all error signals of closed loop system are uniformly bounded finally under this control strategy. Nonlinear simulation verifies the feasibility and validity of this control strategy to the RBV control system.

1. Introduction

To meet the development of space research, space tourism, and military requirement and achieve the goal of speediness, high reliability, reusability, and low cost, the hypersonic aerospace vehicle especially reusable launch vehicle, RLV, emerges [1–6].

Reusable boosted vehicle (RBV) experiences the subsonic, transonic, and supersonic phase during the whole flight, which the aerodynamic coefficients, dynamic pressure, and flight altitude acute change, especially in the large attitude adjusting phase with supersonic and large angle of attack. Considering the imprecise aerodynamic model, abominable flight condition at the high altitude, great system perturbation, and interference, gain scheduling and PID control strategy based on linearized with small disturbances cannot apply to the flight control system of RBV large attitude adjusting phase design. It is necessary to design RBV control system by using nonlinear control method.

Shtessel designed the sliding mode control system of X-33 based on the time-scale separation principle, which has achieved the great control performance [7–9]. On the basis, the designer estimated the real-time perturbation and interference through introducing the sliding mode observer, which not only could suppress the buffeting, but also could improve the robust performance of system. In case of solving the buffeting problem of sliding mode control method effectively, it could be one of the efficient methods to solve the uncertain nonlinear system.

Linear parameter varying (LPV) control methodology [10] is an extension of H_∞ control theory [11, 12] to the linear varying parameter system. To the nonlinear flight control system, many scholars have studied the application of LPV control methodology [13–15]. Nevertheless, using LPV control methodology needs to transform the nonlinear system to the LPV system, there is no uniform evaluation criterion to judging the approximative transform.

Nonlinear dynamic inversion (NDI) is the general nonlinear control strategy and methodology. Snell et al. [16] applied NDI to the supermaneuverable aircraft firstly. Bugajski and Enns [17] designed the universal architecture of flight control system design, the core of which was the structure block. Using the above method designed the control law of the large angle of attack aircraft. The simulation results verified that this methodology could satisfy the performance requirement of supermaneuvering flight control, but it must be pointed out that modeling error and serious unusual aerodynamic effect cause the decreased robustness in the NDI control law. Farland and D’Souza [18] designed the attitude control system of lifting body reentry vehicle by NDI. The writer indicated that, to the parameter perturbation and external interference, using robust control theory strengthens the robustness of system under the NDI. NDI control methodology requires the accurate model. In fact it is impossible. Hence, it is necessary to combine the other control methods to eliminate the influence of inaccurate model.

2. Flight Timing and Trajectory of RBV

The RBV in this paper is the reusable vehicle which uses the rocket back to the launch site. Its flight processes as follows: after the separation from the disposable core stage (upper stage), RBV adjusts the attitude under RCS system in the tail during the sliding by inertia itself. When attitude angle of RBV reaches about 180°, the adjust phase finishes, and the head of RBV points to the direction of returning to the launch site. After the adjusting phase, with secondary ignition of RBV rocket engine (restricting the overload of secondary shut-off point), varying thrust regulator is used to adjust the flight velocity to satisfy the constraint condition of reentry. Afterwards, the vehicle experiences the fixed attitude dropping phase and the adjusting attitude phase and then enters the energy management and autonomous landing phase. The flight timing and trajectory of the RBV are shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Flight profile of RBV.

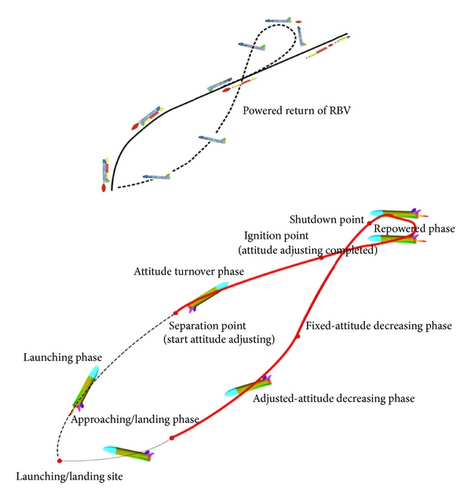
Reusable boosted vehicle (RBV) experiences the subsonic, transonic, and supersonic phase during the whole flight, which the aerodynamic coefficients, dynamic pressure, and flight altitude change acutely. For this, the differences of the dynamic characteristics of RBV are significant during all of the flight phase. Besides that, there is a great different between the aerodynamic characteristics of RBV and the conventional vehicle. This paper focuses on the large attitude adjusting phase after the RBV separating between the core stages. To implement the high reliability and precision of RBV, the nonlinear model is built according to the flight environment.

3. RBV System Modeling

This paper examines the problem of a nonaxisymmetric airframe which is flown in a large angle of attack. In the trajectory tracking problem (see Figure 2, body coordinate system of RBV), and the guidance law produces acceleration commands in the body y and z axes based on nominal trajectory. These acceleration commands can be converted into commands in roll angle and angle of attack, which are fed into the autopilot. The task of the controller is to track commands in angle of attack and roll angle, while keeping sideslip angle small. There are many examples of angle of attack autopilots in the literature. The reader is referred to [16, 19] for treatments of autopilots that control angle of attack.

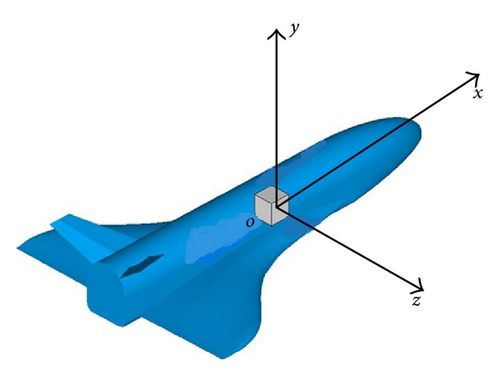
3.1. Dynamic Model for Attitude Adjusting Phase of RBV

Considering the assumption of designing the flight control system of X-33 [20], HOPE-X Series [21–23], the rigid-body nonlinear equations of motion for RBV of constant mass based on the body coordinate system of RBV and According to the coordinate system definition of [24], the rigid-body nonlinear equations of motion for RBV of constant mass is as follows:

(1)

where

and

are the system state variable and then

are also the system output;

and

are the control variable;

is the parameter vector;

and

are the nonlinear differential function; g_s2 (Θ, Ω) ∈ R^3×3 and g_f (Θ, Ω, w) ∈ R^3×3 are the control matrix; g_s1 (Θ, Ω) represents the deflections of aerodynamic surfaces and control moment of RCS.

3.2. Aerodynamic Data Model of RBV

In order to design the flight control system of RBV in this paper conveniently, aerodynamic data models of RBV are built in the velocity coordinate system, and body coordinate system respectively [25].

Aerodynamic coefficient in the velocity coordinate system is as follows:

(2)

where Δ (·) is the term of aerodynamic perturbation; Ma is the Mach number; δ_aero is the command of aerodynamic surfaces.

Aerodynamic moment coefficient in the body coordinate system:

(3)

where Δ (·) is the term of aerodynamic perturbation; b is the span; c is the mean aerodynamic chord.

4. Robust Adaptive Inversion Control Based on Neural Network

4.1. Single Hidden Layer Neural Network

The structure of the single hidden layer [26, 27] is shown in Figure 3, the input and output of which are defined:

(4)

(5)

where

is the input of neural network, which belongs to the certain compact set

; the output of neural network is

;

and

are the weight of the input layer to hidden layer and the hidden layer to the output layer, respectively; n₁, n₂, and n₃ are the number of the input, the neurons in the hidden layer, and the output respectively.

Action function σ (·) is chosen Sigmoid function and

(6)

where

(7)

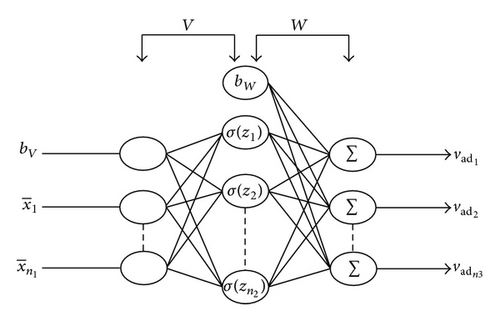
In addition, the offset term b_V, b_W ≥ 0 in (4) and (6), the objective of which is to contain the threshold value of neurons in the hidden layer and to contain the output layer to the weight matrix, to implement the real-time adjusting of the threshold value of neurons.

4.2. Nonlinear Dynamic Inversion

The basic idea of the nonlinear dynamic inversion method [28–30] is to transform the dynamics of nonlinear system to a linear one through the inverse system of the controlled object and then implement the integrated system under the theory of the linear system. The general nonlinear system is described as follows:

(8)

where x ∈ Rⁿ is the system state variable; u ∈ R^m is the system control variable; y ∈ R^l is the system output variable.

The objective of control system design of nonlinear system as (8) is to seek the control input u, through which the system output y could track the expected output and time-varying trajectory y_d according to the certain precision and ensure the all the state variable of the closed loop be bounded.

Performing the derivation to (8),

(9)

(10)

Under the above control, the result of the ith output subsystem is as follows:

(11)

where v_i is called pseudocontrol input variable generally. The conventional nonlinear system in (8) could be transformed the linear system in (11) through (9)~(10).

Defining the tracking error e_i = y_i − y_di and choosing the pseudocontrol variable:

(12)

Hence, the dynamic equation of tracking error in the ith closed loop subsystem is as follows:

(13)

Selecting the coefficients

to configurate all characteristic roots of

lying on the open left plane, namely, to ensure the stability of the ith closed loop subsystem. The dynamic equation of tracking error in the entire closed loop system is as follows:

(14)

where the definitions of K and E are referenced in [31]. The block diagram of dynamic inverse method is shown in Figure 4.

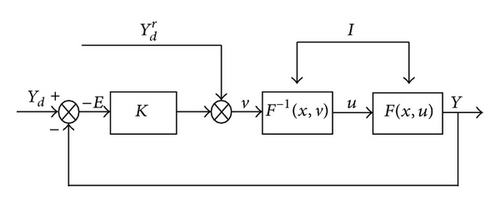
4.3. System Control Strategy

In (8), there are many inexact factors in the nonlinear system such as unmodeled dynamic, parameter perturbation, and external disturbance. Considering that the nonlinear dynamic inversion needs the accurate system model, the control strategy to counteract the model uncertainty must be proposed to guarantee the system tracking performance based on the nonlinear dynamic inversion method.

Let the nominal value of F (x, u) be

; (10) is:

(15)

Transforming the system uncertainty to the system inverse error Δ (x, v),

(16)

The dynamic equation of the tracking error in entire closed loop system is

(17)

where A = −K.

Use the nonlinear approximation of neural network maps the inverse error Δ (x, v) resulting from the system uncertainty to compensate the uncertain model [31]. Meanwhile, the error caused by the approximation inverse error of the neural network is suppressed by robust adaptive method. Hence, the definition of the robust adaptive inverse control strategy based on neural network is as follows:

(18)

where

(19)

where u is the actual system control input; v is the virtual system control input;

is the r order derivative of system reference input, which is similar to definition in [32]; v_sc is the static control compensator; v_ad is the neural network output; v_rb is the robust adaptive term.

Under effecting of the control strategy (18), the dynamic error equation of closed loop from (19) is

(20)

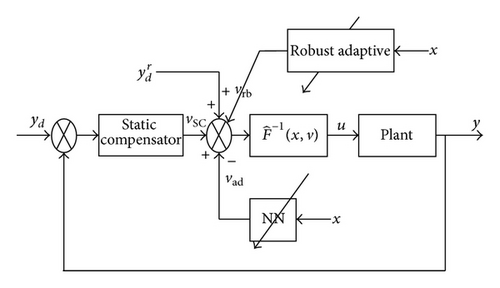
The robust adaptive inversion control based on neural network is shown in Figure 5.

Based on the above theory, the control law design of the entire closed loop system is made up by the following three steps:

(1)
Firstly, the static compensator v_sc designed by nonlinear dynamic inversion method is exponent stable in the nominal neighborhood and satisfies the performance requirements of closed loop system in the nominal condition (i.e., Δ = 0);
(2)
Secondly, according to the strong nonlinear mapping ability of neural network, the inverse error Δ (x, v) mapped by uncertainty Δ (x, u) is approximated by neural network output v_ad when uncertainty condition exists.
(3)
Finally, designing the robust adaptive control term v_rb overcomes the influence of approximation error, then a better adaptive robust performance of entire closed loop system is achieved.

5. Analysis and Design of Control System

Based on the control strategy in the above third chapter, the neural network robust adaptive inversion control law is designed. And then, the stability of the closed loop system is proved strictly in the theory. Here, the input of SHLNN is , where E = x − x_d, x is the system state, x_d is the expected system state, and v_ad is the neural network output.

Assumption 1. Giving arbitrary , there are the ideal neural network weight matrixes V^* and W^* to make the single hidden neural network uniform approximating the inverse error function Δ(x, v) which is continuous and derivable in the compact set . That is,

(21)

where

;

is the approximation error and satisfies

(22)

Assumption 2. Generally speaking, the ideal neural network weight matrixes V^* and W^* are unknown and may be not only. Therefore V^* and W^* can be defined:

(23)

where

(24)

where ∥·∥_F is Frobenius norm and

are the positive constant.

For ideal weight matrixes V^*and W^* being unknown, let and be defined to describe the estimated value of neural network ideal weight matrix.V₀ and W₀ are the initial value of network, where and are the estimated error of neural network weight, respectively. Based on this estimated value, the online neural network approximation v_ad is

(25)

Now the dynamic error equation of closed loop system is

(26)

As A is Hurwitz matrix, there exists only positive definite matrix P with respect to the following Lyapunov function, which satisfies

(27)

where Q is an arbitrary positive definite matrix.

Considering the Taylor expansion of in ,

(28)

Here, let

(29)

Hence,

in (26) is changed to

(30)

where

(31)

Synthesizing (30) and (31)

(32)

where ∥·∥_F is Frobenius norm; ∥·∥ is Euclid norm; ∥·∥₁ is 1 norm; ones

is the 1 matrix. The upper bound of w is expressed as the following form:

(33)

where

(34)

Substituting (26) by Taylor expansion of network approximation inverse error, the dynamic error equation of the closed loop system is as follows:

(35)

Introducing the operator vec to the matrix M ∈ R^n×m, in order to analysis the following theory conveniently,

(36)

where col_i(M) is the ith column of the matrix M.

Let . Considering the composite errors vector , the compact set defined as follows is

(37)

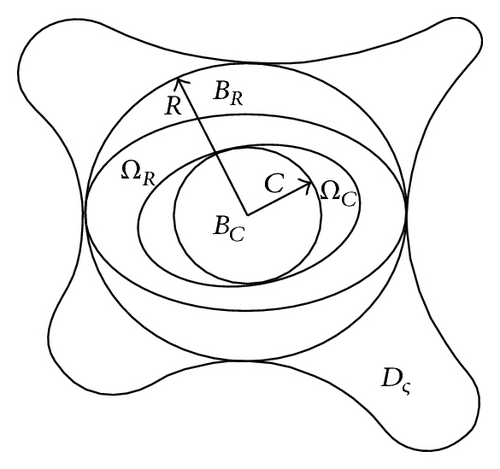
Assumption 3. B_R is the largest hypersphere in compact set D_ς and satisfies

(38)

where λ_max⁡(T) and λ_min⁡(T) are the maximum and minimum characteristics value of the matrix T, respectively. And the T is:

(39)

where Γ_W and Γ_V are positive definite matrixes and γ_ψ > 0.

Let v_R be the minimum value given by following function V along the bound of hypersphere B_R:

(40)

Define the following compact set:

(41)

Theorem 4. To the nonlinear uncertain system composed by (8), (15), and (18), the following designed control law based on neural network robust adaptive dynamic inversion satisfies all the error signals ς(t) uniformly bounded considering the conditions of Assumptions 1–3 when the initial value ς(0) of composite errors belongs to the compact set Ω_R. When t > T₀, the trajectory of arbitrary initial error signals from Ω_R will enter the boundary of Ω_C in the finite time, the final value of which is ,

(42)

where u is the actual system control input; v is the virtual system control input;

is the derivative of system reference input; v_sc is the static control compensator; v_ad is the neural network output; v_rb is the robust adaptive term, and

(43)

where A is Hurwitz matrix and ξ = E^TPB and B = I_m satisfy (26). The following neural network adaptive law and robust adaptive law are

(44)

where s^* = 1 + s_w;

; ψ is the estimated value of

; ψ₀ is the initial value of ψ;

; Γ_V and Γ_W are positive definite matrixes; γ_ψ > 0, λ_V > 0, λ_W > 0, and Υ > 0.

Proof. The Lyapunov function of system is

(45)

Solving the time derivative of (45) and using (27) and (35) yield

(46)

Substituting the neural network robust adaptive dynamic inversion control law (42)~(45) to (46) yields

(47)

Simplifying the above equation,

(48)

Amplifying (48) according to the conditions of s^* = 1 + s_w and yields

(49)

Simplifying (49) based on the given estimated error yields

(50)

Using the following inequality,

(51)

Simplifying (50) yields

(52)

where λ_min⁡(Q) is the minimum characteristics value of Q.

Combining with [33, 34]:

(53)

Giving definitions as follows:

(54)

(55)

Equation (55) can be written:

(56)

From (56), it is obvious that when satisfying the following inequality:

(57)

(58)

From (57), it is obvious that if we satisfy the , (58) must be established, which indicates that there is a compact set. In the out of the compact set, is established. Defining the compact set proves that all of the error signals are ultimately bounded. Defining the following the hypersphere [35] firstly is

(59)

There is beyond the compact set B_C. From (44), it yields

(60)

Let v_C be the maximum of function V along the boundary of the hypersphere B_C:

(61)

The compact set Ω_C is

(62)

From (38) and Figure 6, it can be proved that B_C ⊂ Ω_C ⊂ Ω_R ⊂ B_R. If the composite initial errors ς(0) ∈ Ω_R, all of the error signals are ultimately bounded in the closed loop system. According to the Lyapunov stability theorem, when t > T₀, the trajectory of arbitrary initial error signals from Ω_R will enter the boundary of Ω_C in the finite time, the final value of which is . The proof is finished.

6. Simulation and Validation of RBV

On the basis of robust adaptive dynamic inversion control strategy in the above chapter and the established RBV model, the simulation verifies the proposed control law of neural network robust adaptive inversion validity. The perturbations are added to the simulation. The attitude tracking commands are produced by guidance module in simulation. When considering the uncertainty, the double loop system determined by (1) is described as follows:

(63)

where

represent the uncertain factors, like the parameter perturbations and external interferences, in the fast loop, and slow loop respectively. To simplifying the design, assuming that Δ_s = 0, the neural network robust adaptive inversion control law to the fast loop is given. As the influence of fast loop is greater than the slow loop, the simplification is reasonable. According to the control mode of fast loop and slow loop of nonlinear dynamic inversion and the control law described in (42), the control input and output of fast loop when Δ_f exists are as follows:

(64)

where

, and f_f reference [31].

and

exist during flight process of RBV; v_rbf, v_adf represent the robust adaptive term and approximation output of fast loop, respectively. The structure diagram of RBV control system is shown in Figure 7.

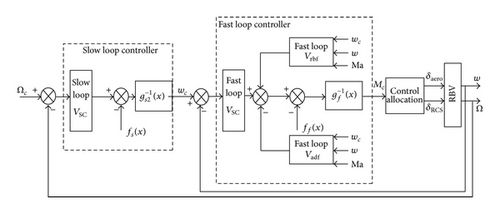
The parameter setting and initial condition of system simulation reference [31]. The simulation results of command angle tracking during large attitude adjusting phase are shown in Figure 8.

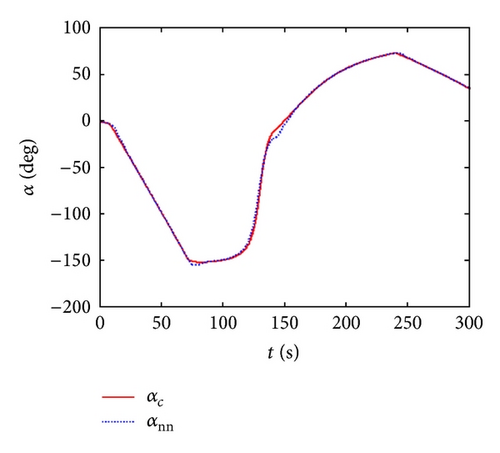
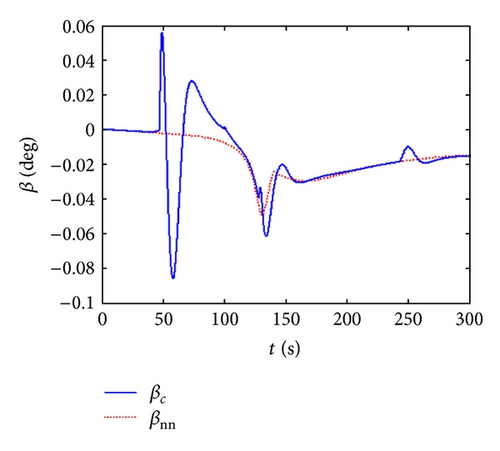
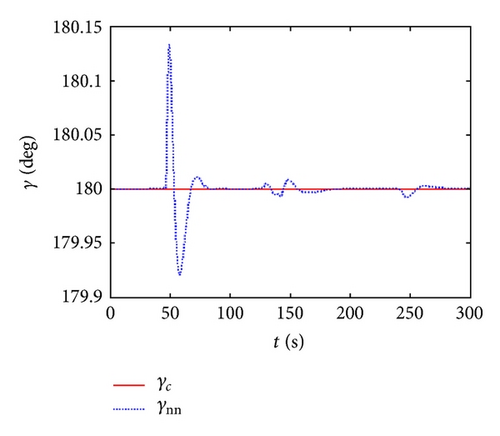
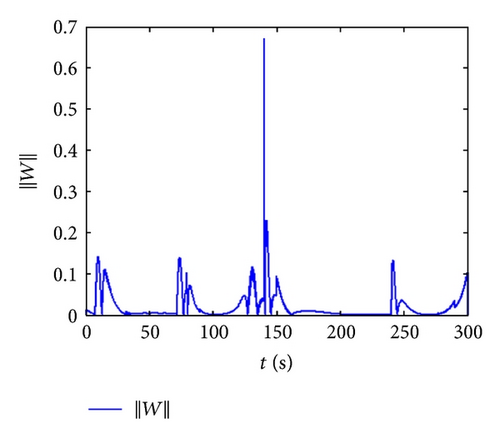
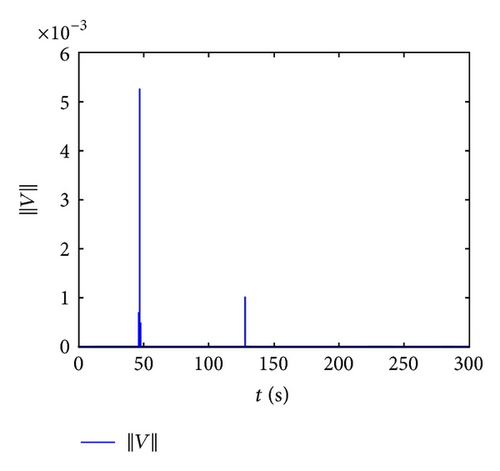
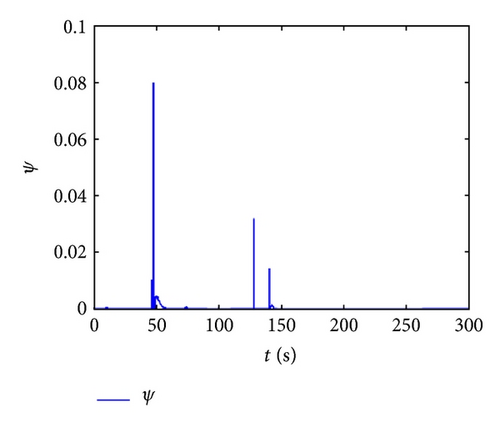
Figure 8 indicates the whole flight simulation curves of RBV control system during the turn period and reentry phase the produced from guidance module which is the control system total input signals. The subscript “nn” represents the simulation results proposed by neural network robust adaptive inversion control law when aerodynamic parameter perturbation exists. “c” is the initial command value. ∥V∥, ∥W∥ are the weight norm of neural network matrixes.

Figure 8 presents the simulation curves of RBV flight control based on neural network robust adaptive inversion. From the curves of guidance command tracking, the system output can track the change of system input finally. The sideslip angle and roll angle have the tracking errors during the attitude adjusting phase for 46.9 s, but both are in the tolerance range. Besides, after accomplishing the adjusting phase at 140 s, the thrust increasing produces some oscillations, which have great influence on angle of attack, but little to sideslip angle and roll angle. The errors of sideslip angle and roll angle are in the tolerance range, and when it is higher than 80 km, the error of angle of attack has little influence on the final tracking effect. From above figures, it can be proved that the final tracking accuracy is high. Analyzing the weight norm and robust adaptive coefficients, the neural network adaptive law is effective and can eliminate the inverse errors. The network weight coefficients not only represent the parameter perturbation and the influence caused by parameter perturbation with varying as system adaptive change, but also represent the influence of eliminating the inverse errors which tended to be stable.

7. Conclusions

According to the uncertainty of RBV model, the robust adaptive inversion control strategy based on neural network is proposed in this paper. The nonlinear simulation verifies the validity to this methodology. Using Lyapunov theory proves the ultimate uniform boundedness of RBV closed loop control system. The simulation results indicate that when aerodynamic moment parameter perturbation is 30%, this methodology can reduce the requirement of RBV model accuracy and improve the control system robustness during the adjusting phase and reentry phase of RBV.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This research was supported under National Natural Science Foundation of China (no. 11372080), China Postdoctoral Science Foundation (no. 20110491028), Central University Foundation of Basic Scientific Research (no. HEUCFZ1126, no. HEUCFZ1120), and Natural Science Foundation of Heilongjiang Province (no. QC2011C020). The authors thank Professor CUI Naigang and CHEN Weidong for their help. Also the authors are indebted to CHEN Yangyang, TANG Xiaoping, and ZENG Kui for their continuous help. Finally, the authors thank the reviewers for their helpful comments and insight.

References

1 Hank J. M., Murphy J. S., and Mutzman R. C., The X-51A Scramjet Engine flight demonstration program, Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, May 2008, Dayton, Ohio, USA, 2-s2.0-77958452194.
Google Scholar
2 Wallace J. G., Bradford J., Charania A. C., Escher W. J. D., and Eklund D., Concept study of an ARES hybrid-OS launch system, Proceedings of the 14th AIAA/AHI International Space Planes and Hypersonics Systems Technologies Conference, November 2006, 1477–1494, 2-s2.0-33947256857.
Google Scholar
3 Kauffmann J., Future European launch systems in the FLPP overview and objectives, Proceedings of the 57th AIAA International Astronautical Congress (IAC ′06), October 2006, Valencia, Spain, 7618–7623, 2-s2.0-40749092843.
Google Scholar
4 Tomatis C., Bouaziz L., Franck T., and Kauffmann J., RLV candidates for European Future Launchers Preparatory Programme, Acta Astronautica. (2009) 65, no. 1-2, 40–46, 2-s2.0-67349240921, https://doi.org/10.1016/j.actaastro.2009.01.057.
10.1016/j.actaastro.2009.01.057
Web of Science® Google Scholar
5 Sippel M., Manfletti C., and Burkhardt H., Long-term/strategic scenario for reusable booster stages, Acta Astronautica. (2006) 58, no. 4, 209–221, 2-s2.0-29244433181, https://doi.org/10.1016/j.actaastro.2005.09.012.
10.1016/j.actaastro.2005.09.012
Web of Science® Google Scholar
6 Sippel M., Atanassov U., Klevanski J., and Schmid V., First-stage design variations of partially reusable launch vehicles, Journal of Spacecraft and Rockets. (2002) 39, no. 4, 571–579, 2-s2.0-0036652575.
10.2514/2.3846
Web of Science® Google Scholar
7 Shtessel Y., Tournes C., and Krupp D., Reusable launch vehicle control in sliding modes, Proceedings of the AIAA Guidance, Navigation, and Control Conference, August 2005, New Orleans, La, USA, 2915–2940, 2-s2.0-29744446910.
Google Scholar
8 Shtessel Y., McDuffie J., Jackson M., Hall C., Gallaher M., Krupp D., and Hendrix N. D., Sliding mode control of the X-33 vehicle in launch and re-entry modes, Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, 1998, Boston, Mass, USA.
Google Scholar
9 Shtessel Y., Hall C., and Jackson M., Reusable launch vehicle control in multiple time scale sliding modes, Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, August 2000, Denver, Colo, USA.
Google Scholar
10 Zhang L. and Shi P., l₂-l_∞ model reduction for switched LPV systems with average dwell time, IEEE Transactions on Automatic Control. (2008) 53, no. 10, 2443–2448, 2-s2.0-56649099174, https://doi.org/10.1109/TAC.2008.2007860.
10.1109/TAC.2008.2007860
Web of Science® Google Scholar
11 Zhang L. and Shi P., Stability, l₂-gain and asynchronous H_∞ control of discrete-time switched systems with average dwell time, IEEE Transactions on Automatic Control. (2009) 54, no. 9, 2192–2199, 2-s2.0-70349435922, https://doi.org/10.1109/TAC.2009.2026841.
10.1109/TAC.2009.2026841
Web of Science® Google Scholar
12 Zhang L., Shi P., Boukas E.-K., and Wang C., H_∞ model reduction for uncertain switched linear discrete-time systems, Automatica. (2008) 44, no. 11, 2944–2949, 2-s2.0-55049112642, https://doi.org/10.1016/j.automatica.2008.03.025.
10.1016/j.automatica.2008.03.025
Web of Science® Google Scholar
13 Ndres, Murry K., Gabriele D. Z., Luis F. P. et al., Application of LPV/LFT modeling and data-based validation to a re-entry vehicle, Proceedings of the AIAA Guidance, Navigation, and Control Conference, August 2009, Chicago, Ill, USA, 2-s2.0-78049263543.
Google Scholar
14 Menon P. P., Prempain E., Postlethwaite I., Bates D., and Bennani S., An LPV loop shaping controller design for the NASA-HL-20 re-entry vehicle, Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, August 2009, Chicago, Ill, USA, 2-s2.0-78049264006.
Google Scholar
15 Menon P. P., Prempain E., Postlethwaite I., Bates D., and Bennani S., Nonlinear worst-case analysis of an LPV controller for approach-phase of a re-entry vehicle, Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, August 2009, 2-s2.0-78049298282.
Google Scholar
16 Snell, Enns D. F., and Garrard W. L., Nonlinear inversion flight control for a super maneuverable aircraft, Proceedings of the AIAA Guidance, Navigation and Control Conference, 1990, Portland, Ore, USA.
Google Scholar
17 Bugajski D. and Enns D., Nonlinear control law with application to high angle-of-attack flight, Journal of Guidance, Control, and Dynamics. (1992) 15, no. 3, 761–767, 2-s2.0-0026856998.
10.2514/3.20902
Web of Science® Google Scholar
18 Farland M. B. and D’Souza C. N., Missile flight control with dynamic inversion and structured singular value synthesis, Proceedings of the AIAA Guidance, Navigation, and Control Conference, 1994, Washington, DC, USA, 544–550.
Google Scholar
19 Carter L. H. and Shamma J. S., Gain-scheduled bank-to-turn autopilot design using linear parameter varying transformations, Journal of Guidance, Control, and Dynamics. (1996) 19, no. 5, 1056–1063, 2-s2.0-0030241128.
10.2514/3.21745
Web of Science® Google Scholar
20 Burken J. J., Lu P., and Wu Z., Reconfigurable flight control designs with application to the X-33 vehicle, Proceedings of the Guidance, Navigation, and Control Conference, 1999, Portland, Ore, USA.
Google Scholar
21 Minami Y., Ishimoto S., Mori T., and Fujii K., Design study on a small-sized partially reusable launch system, Proceedings of the 13th AIAA/CIRA International Space Planes and Hypersonic Systems and Technologies Conference, May 2005, 471–482, 2-s2.0-29044434981.
Google Scholar
22 Fujii K. and Ishimoto S., Research activities to realize advanced space transportation system, Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, May 2008, 2-s2.0-77958481881.
Google Scholar
23 Goto N., Kawakita T., and Kawaguchi J., Nonlinear dynamical analysis for a reentry vehicle, Transactions of the Japan Society for Aeronautical and Space Sciences. (2004) 47, no. 156, 99–107, 2-s2.0-33747705469, https://doi.org/10.2322/tjsass.47.99.
10.2322/tjsass.47.99
Web of Science® Google Scholar
24 Jia P. R., Chen K. J., and He L., Ballistics of Long Range Missiles, 1993, National University of Defense Technology Press, Changsha, China.
Google Scholar
25 Ha Q. P., Nguyen Q. H., Rye D. C., and Durrant-Whyte H. F., Fuzzy sliding-mode controllers with applications, IEEE Transactions on Industrial Electronics. (2001) 48, no. 1, 38–46, 2-s2.0-0035248596, https://doi.org/10.1109/41.904548.
10.1109/41.904548
Web of Science® Google Scholar
26 Alise J. and Eric N., Reusable launch vehicle adaptive guidance and control using neural networks, Proceedings of the AIAA Guidance, Navigation, and Control Conference, August 2001, Montreal, Canada.
Google Scholar
27 Zhang L., Gao H., and Kaynak O., Network-induced contraints in networked control system: a survey, IEEE Transcations on Industrial Informatics. (2013) 9, no. 1, 403–416.
10.1109/TII.2012.2219540
Web of Science® Google Scholar
28 Bugajski D. and Enns D., Nonlinear control law with application to high angle-of-attack flight, Journal of Guidance, Control, and Dynamics. (1992) 15, no. 3, 761–767, 2-s2.0-0026856998.
10.2514/3.20902
Web of Science® Google Scholar
29 Enns F., Bugajski D. J., Hendrick R. et al., Dynamic inversion: an evolving methodology for flight control, International Journal of Control. (1994) 59, no. 1, 71–91.
10.1080/00207179408923070
Web of Science® Google Scholar
30 Da Costa R. R., Chu Q. P., and Mulder J. A., Reentry flight controller design using nonlinear dynamic inversion, Journal of Spacecraft and Rockets. (2003) 40, no. 1, 64–71, 2-s2.0-0037284889.
10.2514/2.3916
Web of Science® Google Scholar
31 Jiangtao X., Research on Attitude Control and Control Allocation for Reusable Boosted Vehicle, 2010, School of Aeronautics, Harbin Institute of Technology, Harbin, China, Chinese.
Google Scholar
32 McFarland and Calise A. J., Multilayer neural networks and adaptive control of agile anti-air missile, Proceedings of the AIAA Guidance, Navigation, and Control Conference, 1997, New Orleans, La, USA.
Google Scholar
33 Polycarpou M. M. and Ioannou P. A., Modelling, identification and stable adaptive control of continuous-time nonlinear dynamical systems using neural networks, Proceedings of the American Control Conference, June 1992, 36–40, 2-s2.0-0027068689.
Google Scholar
34 Polycarpou M. M. and Mears M. J., Stable adaptive tracking of uncertain systems using nonlinearly parametrized on-line approximators, International Journal of Control. (1998) 70, no. 3, 363–384, 2-s2.0-0032096256.
10.1080/002071798222280
Web of Science® Google Scholar
35 Madyastha K., Adaptive estimation for control of uncertain nonlinear system with applications to target tracking [Ph.D. dessertation], 2005, Georgia Institute of Technology, Atlanta, Ga, USA.
Google Scholar

All articles

Research on RBV Control Strategy of Large Angle Maneuver

Abstract

1. Introduction

2. Flight Timing and Trajectory of RBV

3. RBV System Modeling

3.1. Dynamic Model for Attitude Adjusting Phase of RBV

3.2. Aerodynamic Data Model of RBV

4. Robust Adaptive Inversion Control Based on Neural Network

4.1. Single Hidden Layer Neural Network

4.2. Nonlinear Dynamic Inversion

4.3. System Control Strategy

5. Analysis and Design of Control System

6. Simulation and Validation of RBV

7. Conclusions

Conflict of Interests

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Research on RBV Control Strategy of Large Angle Maneuver

Abstract

1. Introduction

2. Flight Timing and Trajectory of RBV

3. RBV System Modeling

3.1. Dynamic Model for Attitude Adjusting Phase of RBV

3.2. Aerodynamic Data Model of RBV

4. Robust Adaptive Inversion Control Based on Neural Network

4.1. Single Hidden Layer Neural Network

4.2. Nonlinear Dynamic Inversion

4.3. System Control Strategy

5. Analysis and Design of Control System

6. Simulation and Validation of RBV

7. Conclusions

Conflict of Interests

Acknowledgments

References

Figures

References

Related

Information