The goal of this paper is to investigate the blow-up and the global existence of the solutions to the discrete p-Laplacian parabolic equation u_t(x, t) = Δ_p,wu(x, t) + λ|u(x, t)|^p−2u(x, t), (x, t) ∈ S × (0, ∞), u(x, t) = 0, (x, t) ∈ ∂S × (0, ∞), u(x, 0) = u₀, depending on the parameters p > 1 and λ > 0. Besides, we provide several types of the comparison principles to this equation, which play a key role in the proof of the main theorems. In addition, we finally give some numerical examples which exploit the main results.

1. Introduction

A discrete p-Laplacian parabolic equation (a reaction-diffusion system) has found many applications in chemical reactions and biological phenomena. A typical example is an autocatalytic chemical reaction between several chemicals in which the concentration of each chemical grows (or decays) due to diffusion and difference of concentration. In general, many of such phenomena are modeled by

(1)

with some boundary and initial conditions where S is the set of chemicals and p > 1, q > 0. Here, Δ_p,w is the discrete p-Laplace operator on a network S, defined by

(2)

For the continuous case, solutions to the initial value problem of (1) may blow up in a finite time or exist globally for all time, depending on the parameters p > 1, q > 0, and

(see [1–7] and see the book [2] for more information about the various blow-up phenomena). In particular, the case where p = q − 1 > 1 has been known as the critical case at which solutions may blow up or exist globally, depending on the parameter λ.

The goal of this paper is to investigate the blow-up and the global existence of the solutions to the initial value problem of the discrete p-Laplacian parabolic equation

(3)

on a network S with boundary, which is the critical case of (1).

The continuous case of (3) has been studied by many authors. For example, the case where 1 < p < 2 was studied in [3, 6] and the case where p > 2 was studied in [3, 4].

For the discrete case of (1), the authors studied the general theory of the equation for the case p = 2 in [8] and Xin et al. studied the blow-up solutions and global solutions for the case where p = 2 and λ = 1 in [9]. On the other hand, for the case λ ≤ 0 in (1), Chung et al. [10, 11] investigate the positive solutions and extinctive solutions, depending on the parameters p and q. But, the case where p > 1 and λ > 0 in (3) has not been studied yet. Thus, the purpose of this paper is to give a complete solution to such a problem about (3).

The main results of this paper are summarized as follows.

Theorem 1. (i) For p > 2 and λ > λ₀, the solution to

(4)

blows up in a finite time T, for every nonnegative and nontrivial initial data u₀.

Here, λ₀ is the first eigenvalue of the p-Laplace operator Δ_p,w on S. Moreover, it is shown that the blow-up rate of the solution is estimated by

(5)

(ii) For p > 2 and λ ≤ λ₀, the solution to (4) is global, for every nonnegative initial data u₀.

(iii) For 1 < p ≤ 2, the nonnegative solution to (4) is global for every nonnegative initial data u₀. In particular, when 1 < p < 2 and λ < λ₀, there exists T > 0 (extinction time) such that u(x, t) ≡ 0 for all t ≥ T.

Besides, we provide several types of the comparison principles to (4) in Section 2, which play a key role in the proof of the main theorems and we give some numerical examples in the final section which exploit the main results.

2. Preliminaries and Discrete Comparison Principles

In this section, we start with some definitions of graph theoretic notions frequently used throughout this paper (see [8, 12, 13] for more details).

For a graph G = G(V, E) we mean finite sets V of vertices (or nodes) with a set E of two-element subsets of V (whose elements are called edges). The set of vertices and edges of a graph G is sometimes denoted by V(G) and E(G), or simply V and E, respectively. Conventionally, we denote by x ∈ V or x ∈ G the facts that x is a vertex in G.

A graph G is said to be simple if it has neither multiple edges nor loops, and G is said to be connected if, for every pair of vertices x and y, there exists a sequence (called a path) of vertices x = x₀, x₁, …, x_n−1, x_n = y such that x_j−1 and x_j are connected by an edge (called adjacent) for j = 1, …, n.

A graph S = S(V^′, E^′) is said to be a subgraph of G(V, E) if V^′ ⊂ V and E^′ ⊂ E.

A weight on a graph G is a function ω : V × V → [0, +∞) satisfying

(i)
ω(x, x) = 0, x ∈ V,
(ii)
ω(x, y) = ω(y, x) if x ~ y,
(iii)
ω(x, y) = 0 if and only if x≁y.

Here, x ~ y means that two vertices x and y are connected (adjacent) by an edge in E. A graph associated with a weight is said to be a weight graph or a network.

For a subgraph S of a graph G(V, E), the (vertex) boundary ∂S of S is the set of all vertices z ∈ V∖S but adjacent to some vertex in S; that is,

(6)

we denote a graph, whose vertices and edges are in both S and ∂S. Throughout this paper, all subgraphs S and

in our concern are assumed to be simple and connected.

For a function

, the discrete p-Laplacian Δ_p,ω on S is defined by

(7)

for x ∈ S.

The following lemmas are useful throughout this paper.

Lemma 2 (see [14], [15].)For functions , one has the following:

(i)
;
(ii)
.

Lemma 3 (see [14], [15].)For p > 1, there exist λ₀ > 0 and ϕ₀(x) > 0, x ∈ S, such that

(8)

Moreover,

(9)

where

In the above, the number λ₀ is called the first eigenvalue of Δ_p,ω on a network with corresponding eigenfunction ϕ₀ (see [12, 13] for the spectral theory of the Laplacian operators).

The rest of this section is devoted to proving the comparison principles for the discrete p-Laplacian parabolic equation

(10)

where λ > 0 and p > 1, in order to study the blow-up occurrence and global existence, which we begin in the next section.

Now, we state the comparison principles and some related corollaries.

Theorem 4. Let T > 0 (T may be +∞), λ > 0, and p ≥ 2. Suppose that real-valued functions u(x, ·), v(x, ·) ∈ C[0, T) are differentiable in (0, T) for each and satisfy

(11)

Then u(x, t) ≥ v(x, t) for all

Proof. Let T^′ > 0 be arbitrarily given with T^′ < T. Then by the mean value theorem, for each x ∈ S and 0 ≤ t ≤ T^′,

(12)

for some ξ(x, t) lying between u(x, t) and v(x, t). Then it follows from (11) that we have

(13)

for all (x, t) ∈ S × (0, T^′]. Let

be the functions defined by

(14)

where L∶ = max⁡_|r|≤M|r^p−2| and

Then inequality (13) can be written as

(15)

for all (x, t) ∈ S × (0, T^′]. Since

is compact, there exists

such that

(16)

Then we have only to show that

. Suppose that

, on the contrary. Since

on both ∂S × [0, T^′] and

, we have (x₀, t₀) ∈ S × (0, T^′]. Then we have

(17)

Since |ξ^p−2(x, t)| ≤ max⁡_|r|≤M|r^p−2| = L, we have

(18)

Combining (17) and (18), we obtain

(19)

which contradicts (15). Therefore,

for all (x, t) ∈ S × (0, T^′] so that we get u(x, t) ≥ v(x, t) for all

, since T^′ < T is arbitrarily given.

Now, we obtain a strict comparison principle as a corollary.

Corollary 5 (strict comparison principle). In Theorem 4, if u₀(x^*) > v₀(x^*) for some x^* ∈ S, then u(x, t) > v(x, t) for all (x, t) ∈ S × (0, T).

Proof. First, note that u ≥ v on by Theorem 4. Let T^′ > 0 be arbitrarily given with T^′ < T and let be a function defined by

(20)

Then τ(x, t) ≥ 0 for all

. Since |u(x^*, t)|^p−2u(x^*, t)≥|v(x^*, t)|^p−2v(x^*, t) for all 0 < t ≤ T^′, and τ(x^*, 0) > 0, we obtain from inequality (15) that

(21)

for all 0 < t ≤ T^′. Then by the mean value theorem, for each

and t with 0 ≤ t ≤ T^′, it follows that

(22)

and |η(x^*, y, t)| < 2M where

Then inequality (21) gives

(23)

where

. This implies

(24)

Now, suppose there exists (x₀, t₀) ∈ S × (0, T^′] such that

(25)

Then

(26)

Hence, inequality (21) gives

(27)

Therefore,

(28)

that is,

(29)

which implies that τ(y, t₀) = 0 for all

with y ~ x₀. Now, for any

, there exists a path

(30)

since

is connected. By applying the same argument as above inductively we see that τ(x, t₀) = 0 for every

. This gives a contradiction to (24).

For the case 1 < p < 2, it is well known that (10) may not have unique solution, in general, and the comparison principle in usual form as in Theorem 4 may not hold. Instead, with a strict condition on the parabolic boundary we obtain a similar comparison principle as follows.

Theorem 6. Let T > 0 (T may be +∞), λ > 0, and p > 1. Suppose that real-valued functions u(x, ·), v(x, ·) ∈ C[0, T are differentiable in (0, T) for each and satisfy

(31)

Then u(x, t) ≥ v(x, t) for all (x, t) ∈ S × (0, T).

Proof. Let T^′ > 0 and δ > 0 be arbitrarily given with T^′ < T and 0 < δ < min⁡_(x,t)∈Γ[u(x, t) − v(x, t)], respectively, where (called a parabolic boundary).

Now, let a function be a function defined by

(32)

Then τ(x, t) > 0 on Γ. Now, we suppose that

. Then there exists (x₀, t₀) ∈ S × (0, T^′] such that

(i)
τ(x₀, t₀) = 0,
(ii)
τ(y, t₀) ≥ τ(x₀, t₀) = 0, y ∈ S,
(iii)
τ(x, t) > 0, (x, t) ∈ S × (0, t₀).

Then

(33)

since u(y, t₀) − u(x₀, t₀) ≥ v(y, t₀) − v(x₀, t₀). Hence, inequality (31) gives

(34)

which leads to a contradiction. Hence, τ(x, t) ≥ 0 for all (x, t) ∈ S × (0, T^′] so that we have u(x, t) ≥ v(x, t) for all (x, t) ∈ S × (0, T), since δ and T^′ are arbitrary.

3. Blow-Up and Global Existence

In this section, we discuss the blow-up and global existence of the equation

(35)

where λ > 0, p > 1, and the initial data u₀ is nontrivial on S. According to the comparison principle in the previous section, the nonhomogeneous term λ|u(x, t)|^p−2u(x, t) can be written as a simpler form as λu^p−1(x, t), for the case where p ≥ 2.

Definition 7 (blow-up). We say that a solution u to an equation defined on a network blows up in finite time T, if there exists x ∈ S such that |u(x, t)|→+∞ as t↗T⁻.

Theorem 8. For p > 2 and λ > 0, the solution to

(36)

blows up at some T^*, provided that

(37)

Proof. First, we note that u(x, t) > 0 on S × (0, ∞), by the strict comparison principle (Corollary 5). Now, we define a functional by

(38)

Then by (37),

(39)

Multiplying (36) by u and summing up over , we obtain from Lemma 2

(40)

Multiplying (36) by u_t and summing up over

, we obtain from Lemma 2

(41)

Then it follows that

(42)

Moreover, it follows from (42) that

(43)

Now, we introduce a new function

(44)

where M > 0 is a constant to be determined later. Then by (40) we have

(45)

(46)

Moreover,

(47)

Using the Schwarz inequality, we obtain

(48)

where ϵ > 0 is arbitrary. Combining the above estimates (46), (47), and (48), we obtain that, for

(49)

Since J(0) > 0 by assumption, we can choose M > 0 to be large enough so that

(50)

Thus inequality (50) implies that, for t ≥ 0,

(51)

Therefore, it follows that I(t) cannot remain finite for all t > 0. In other words, the solutions u(x, t) blow up at some time T^*.

Remark 9. (i) Condition (37) implies that

(52)

where λ₀ is the first eigenvalue of Δ_p,ω.

(ii) The initial data u₀ with J(0) > 0 always exists. In fact, consider an eigenvalue λ₀ > 0 and eigenfunction ϕ₀(x) > 0 in Lemma 3. Taking u₀(x) = ϕ₀(x), then we have

(53)

where λ > λ₀.

(iii) When the solution to (37) is global, then we must have

(54)

for all t > 0.

(iv) The blow-up time in the above can be estimated roughly. Taking

(55)

we see that

(56)

which implies

(57)

where

. Then the blow-up time T^* satisfies

(58)

Now, we state the main theorem as follows.

Theorem 10. The solution to (36) with p > 2 and λ > λ₀ blows up in finite time, for every nonnegative and nontrivial initial data u₀.

Proof. First, we note that (36) has a unique solution such that

(59)

Take t₀ > 0, k > 0 arbitrarily and consider an equation

(60)

where ϕ₀ is the eigenfunction corresponding to the first eigenvalue λ₀ > 0. Then the initial data v(x, t₀) satisfies

(61)

Then, by Theorem 8, the solution v(x, t) is positive and blows up in a finite time. Since

(62)

for a small k > 0, the comparison principle enables us to see

(63)

which completes the proof.

Remark 11. According to Remark 9 (iv) to Theorem 8, the blow-up time for the solution to (36) is estimated by

(64)

We now derive the lower bound for the maximum function of blow-up solutions.

Theorem 12. Let u be the solutions to (36) blowing up at finite time T. Then it follows that

(65)

for all t > 0.

Proof. For each t > 0, let x_t ∈ S be the node such that

(66)

In fact, we note that u(x_t, t) is continuous on [0, ∞) and differentiable for almost all t > 0. Then (36) can be written as

(67)

for almost all s > 0.

Now define a function by

(68)

Then v(x, t) = v(y, t), t > 0, if x, y ∈ S. Multiplying (67) by u(x_s, s) and summing over

, we obtain, for almost all t > 0,

(69)

or, equivalently,

(70)

Integrating over [t, T], we have

(71)

which is desired.

Now, we state the global existence of the solutions.

Theorem 13. For p > 2 and λ ≤ λ₀, the solution to (36) is global for every nonnegative initial data u₀.

Proof. Consider an eigenvalue λ₀ > 0 and eigenfunction ϕ₀(x) > 0 in Lemma 3 and v(x, t)∶ = Kϕ₀(x), , t ≥ 0. Then by taking K large enough to be Kϕ₀(x) ≥ u₀(x), x ∈ S, we have

(72)

for all t > 0 and x ∈ S. Then by the comparison principle, we see that 0 ≤ u(x, t) ≤ Kϕ₀(x), x ∈ S, t ≥ 0, which is desired.

We have so far discussed the blow-up or the global existence (35) for the case p ≥ 2. Now, we discuss the case 1 < p ≤ 2. Here, we note that when 1 < p < 2, the solution to the equation may not have unique positive solution.

Theorem 14. For 1 < p ≤ 2, the nonnegative solution to

(73)

is global for every λ > 0. In particular, when 1 < p < 2 and λ < λ₀, then there exists T (extinction time) such that u(x, t) ≡ 0 for t ≥ T.

Proof. First, consider ODE

(74)

where

. Then

(75)

Then by the comparison principle (Theorem 6), we see that

(76)

which implies that u(x, t) must be global.

Now, assume 1 < p < 2 and λ < λ₀. When u is a trivial solution, then we are done. So now we assume that u is nontrivial. Multiplying (73) by u, as done in (40), we have

(77)

where the last inequality follows from the elementary inequality

(78)

for t₁, t₂, …, t_n ≥ 0. Now suppose

for t ≥ 0, on the contrary. Since u(x, t) = 0, x ∈ ∂S, t ≥ 0, we obtain

(79)

Integrating (79) over [0, t], we obtain

(80)

which is absurd for large t > 0. Hence, y(T) = 0 for some T > 0 and, therefore, we can conclude that y(t) = 0, t > T, for some T > 0, since y^′(t) ≤ 0 in inequality (79).

Remark 15. (i) When p = 2 in the above, we do not need the assumption that u is nonnegative, which follows automatically from the comparison principle (Theorem 4).

(ii) In fact, inequality (80) gives us the extinction time T, estimated by

(81)

4. Examples and Numerical Illustrations

In this section, we show numerical illustrations to exploit our results in the previous section.

Now, consider a graph S = {x₁, x₂, x₃} with the boundary ∂S = {x₄, x₅} and the weight

(82)

as in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Graph .

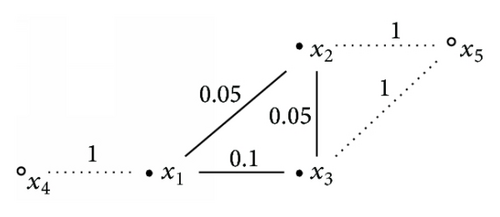
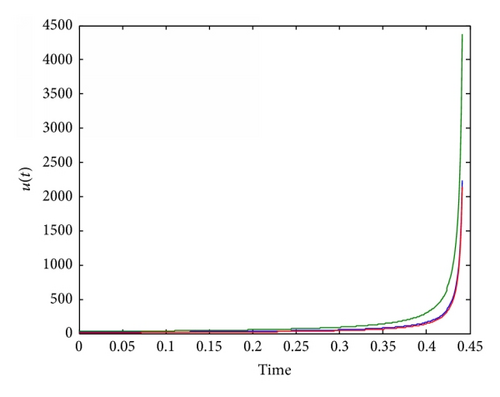
Example 1. For (36) on (Figure 1) graph with p = 3, λ = 1.1, consider initial data given by u₀(x₁) = 20, u₀(x₂) = 30, and u₀(x₃) = 10. Then by easy calculation, we get the first eigenvalue λ₀ = 1 < λ = 1.1 and the corresponding eigenfunction ϕ₀(x₁) = ϕ₀(x₂) = ϕ₀(x₃)≒0.6934. Figure 2 shows that the solution to (36) blows up and the computed blow-up time T is estimated as T≒0.4433079.

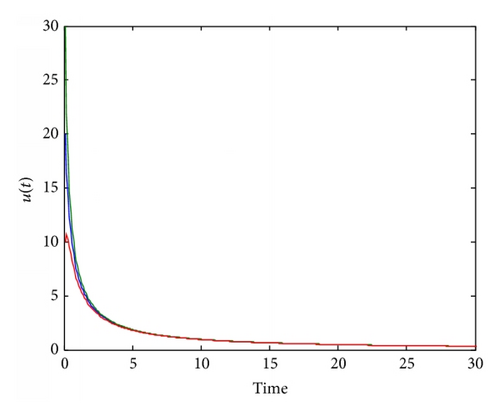
On the other hand, consider the same equation (36) with p = 3, λ = 0.9 and the same initial data. Then λ = 0.9 < λ₀ = 1 and Figure 3 shows that the solution to (36) is global.

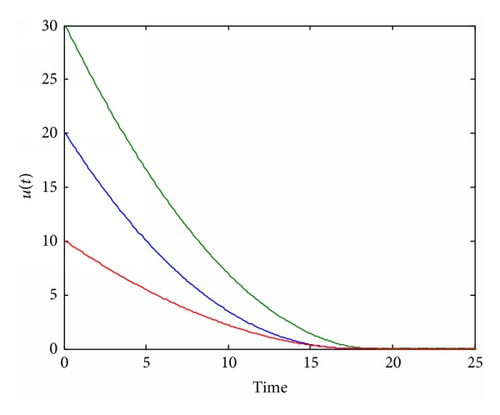
Example 2. For (36) on (Figure 1) graph with p = 1.5, λ = 0.5, and the same initial data u₀ given by u₀(x₁) = 20, u₀(x₂) = 30, and u₀(x₃) = 10, then Figure 4 shows that the solution to (36) is global and extinctive.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MOE) (no. 2012R1A1A2004689) and Sogang University Research Grant of 2014 (no. 201410044).

References

1 Fujii A. and Ohta M., Asymptotic behavior of blowup solutions of a parabolic equation with the p-Laplacian, Publications of the Research Institute for Mathematical Sciences. (1996) 32, no. 3, 503–515.
10.2977/prims/1195162854
Web of Science® Google Scholar
2 Hu B., Blow-up Theories for Semilinear Parabolic Equations, 2011, 2018, Springer, Berlin , Germany, Lecture Notes in Mathematics, MR2796831.
10.1007/978-3-642-18460-4
Web of Science® Google Scholar
3 Liu W., A note on blow-up for fast diffusive p-Laplacian with sources, Mathematical Methods in the Applied Sciences. (2009) 32, no. 2, 241–245, MR2478915, 2-s2.0-59349102334, https://doi.org/10.1002/mma.1035.
10.1002/mma.1035
Web of Science® Google Scholar
4 Li Y. and Xie C., Blow-up for p-Laplacian parabolic equations, Electronic Journal of Differential Equations. (2003) no. 20, 1–12.
Web of Science® Google Scholar
5 Tsutsumi M., Existence and nonexistence of global solutions for nonlinear parabolic equations, Research Institute for Mathematical Sciences. Publications. (1972) 8, no. 2, 211–229, https://doi.org/10.2977/prims/1195193108, MR0312079.
10.2977/prims/1195193108
Google Scholar
6 Yin J. and Jin C., Critical extinction and blow-up exponents for fast diffusive p-Laplacian with sources, Mathematical Methods in the Applied Sciences. (2007) 30, no. 10, 1147–1167, https://doi.org/10.1002/mma.833, MR2329637, 2-s2.0-34250315016.
10.1002/mma.833
Web of Science® Google Scholar
7 Zhao J. and Liang Z., Blow-up rate of solutions for p-Laplacian equation, Journal of Partial Differential Equations. (2008) 21, no. 2, 134–140, MR2419368.
CAS Google Scholar
8 Chung S.-Y. and Berenstein C. A., ω-harmonic functions and inverse conductivity problems on networks, SIAM Journal on Applied Mathematics. (2005) 65, no. 4, 1200–1226, https://doi.org/10.1137/S0036139903432743, MR2147325, 2-s2.0-25144506689.
10.1137/S0036139903432743
Web of Science® Google Scholar
9 Xin Q., Xu L., and Mu C., Blow-up for the ω-heat equation with Dirichlet boundary conditions and a reaction term on graphs, Applicable Analysis. (2014) 93, no. 8, 1691–1701, https://doi.org/10.1080/00036811.2013.842640.
10.1080/00036811.2013.842640
Web of Science® Google Scholar
10 Chung Y.-S., Lee Y.-S., and Chung S.-Y., Extinction and positivity of the solutions of the heat equations with absorption on networks, Journal of Mathematical Analysis and Applications. (2011) 380, no. 2, 642–652, MR2794420, https://doi.org/10.1016/j.jmaa.2011.03.006, 2-s2.0-79955037976, ZBL1219.35024.
10.1016/j.jmaa.2011.03.006
Web of Science® Google Scholar
11 Lee Y.-S. and Chung S.-Y., Extinction and positivity of solutions of the p-Laplacian evolution equation on networks, Journal of Mathematical Analysis and Applications. (2012) 386, no. 2, 581–592, https://doi.org/10.1016/j.jmaa.2011.08.023, MR2834768, 2-s2.0-80053133452.
10.1016/j.jmaa.2011.08.023
Web of Science® Google Scholar
12 Chung F. R., Spectral Graph Theory, 1997, American Mathematical Society, CBMS Regional Conference Series in Mathematics, MR1421568.
Google Scholar
13 Cvetković D. M., Doob M., and Sachs H., Spectra of Graphs: Theory and Applications, 1980, Academic Press, New York, NY, USA, MR572262.
Web of Science® Google Scholar
14 Park J.-H. and Chung S.-Y., Positive solutions for discrete boundary value problems involving the p-laplacian with potential terms, Computers & Mathematics with Applications. (2011) 61, no. 1, 17–29, 2-s2.0-78649444676, https://doi.org/10.1016/j.camwa.2010.10.026, MR2739432.
10.1016/j.camwa.2010.10.026
Web of Science® Google Scholar
15 Park J.-H. and Chung S.-Y., The Dirichlet boundary value problems for p-Schrödinger operators on finite networks, Journal of Difference Equations and Applications. (2011) 17, no. 5, 795–811, 2-s2.0-79957443257, https://doi.org/10.1080/10236190903376204, MR2795526.
10.1080/10236190903376204
Web of Science® Google Scholar

Citing Literature

All articles

Critical Blow-Up and Global Existence for Discrete Nonlinear p-Laplacian Parabolic Equations

Abstract

1. Introduction

2. Preliminaries and Discrete Comparison Principles

3. Blow-Up and Global Existence

4. Examples and Numerical Illustrations

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Critical Blow-Up and Global Existence for Discrete Nonlinear p-Laplacian Parabolic Equations

Abstract

1. Introduction

2. Preliminaries and Discrete Comparison Principles

3. Blow-Up and Global Existence

4. Examples and Numerical Illustrations

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Related

Information