Volume 2014, Issue 1 704839

Research Article

Open Access

Enhanced Particle Swarm Optimization-Based Feeder Reconfiguration Considering Uncertain Large Photovoltaic Powers and Demands

Ying-Yi Hong,

Corresponding Author

Ying-Yi Hong

[email protected]

orcid.org/0000-0002-9540-3931

Department of Electrical Engineering, Chung Yuan Christian University, Chungli City 320, Taiwan cycu.edu.tw

Search for more papers by this author

Faa-Jeng Lin,

Faa-Jeng Lin

Department of Electrical Engineering, National Central University, Chungli City 320, Taiwan ncu.edu.tw

Search for more papers by this author

Fu-Yuan Hsu,

Fu-Yuan Hsu

Department of Electrical Engineering, Chung Yuan Christian University, Chungli City 320, Taiwan cycu.edu.tw

Search for more papers by this author

Ying-Yi Hong,

Corresponding Author

Ying-Yi Hong

[email protected]

orcid.org/0000-0002-9540-3931

Department of Electrical Engineering, Chung Yuan Christian University, Chungli City 320, Taiwan cycu.edu.tw

Search for more papers by this author

Faa-Jeng Lin,

Faa-Jeng Lin

Department of Electrical Engineering, National Central University, Chungli City 320, Taiwan ncu.edu.tw

Search for more papers by this author

Fu-Yuan Hsu,

Fu-Yuan Hsu

Department of Electrical Engineering, Chung Yuan Christian University, Chungli City 320, Taiwan cycu.edu.tw

Search for more papers by this author

First published: 30 April 2014

https://doi.org/10.1155/2014/704839

Citations: 5

Academic Editor: Ching-Song Jwo

Share a link

Email
Wechat
Bluesky

Abstract

The Kyoto protocol recommended that industrialized countries limit their green gas emissions in 2012 to 5.2% below 1990 levels. Photovoltaic (PV) arrays provide clear and sustainable renewable energy to electric power systems. Solar PV arrays can be installed in distribution systems of rural and urban areas, as opposed to wind-turbine generators, which cause noise in surrounding environments. However, a large PV array (several MW) may incur several operation problems, for example, low power quality and reverse power. This work presents a novel method to reconfigure the distribution feeders in order to prevent the injection of reverse power into a substation connected to the transmission level. Moreover, a two-stage algorithm is developed, in which the uncertain bus loads and PV powers are clustered by fuzzy-c-means to gain representative scenarios; optimal reconfiguration is then achieved by a novel mean-variance-based particle swarm optimization. The system loss is minimized while the operational constraints, including reverse power and voltage variation, are satisfied due to the optimal feeder reconfiguration. Simulation results obtained from a 70-bus distribution system with 4 large PV arrays validate the proposed method.

1. Introduction

The Kyoto protocol mandated that industrialized countries should reduce their greenhouse gas emissions in 2012 to 5.2% below their 1990 levels [1]. The Copenhagen Accord later called for the mitigation of global emissions in order to restrict rises in global temperatures to a maximum of 2°C [2]. To attain a low carbon environment, utilizing renewable energy is essential to provide electric power in power systems. Of all renewable energies, wind-turbine generators (WTG), and solar photovoltaic (PV) can provide the cleanest energy to consumers. Although a single unit size of WTG is generally much larger than that of a PV array, the former requires additional effort in terms of installation and maintenance. WTG is also limited by its produced noise, possibly damaging the ecosystem by altering the migration patterns of birds or other animals. However, solar PV arrays can provide noise-free energy, which may be installed in rural fields and rooftops of houses in urban areas. Solar PV has been widely studied in a power system, including solar power prediction [3], capacity sizing [4], and maximum power point tracking [5, 6]. These works focus only on solar PV modules without addressing system operation problems, which the penetration of solar PV energies in a distribution system causes (e.g., reverse power and high voltages at downstream customers).

Designed as interconnected networks, electric distribution networks are operated in a radial structure. The feeder configuration problem attempts to find a radial operating structure that optimizes network performance while satisfying operation constraints. In practice, distribution system operators may tend to reduce the system real-power loss and enhance voltage quality under normal conditions [7–12]. Jeon and Kim integrated tabu search with the simulated annealing algorithm to minimize system losses in [7]. The tabu search attempts to determine a solution using the greatest-descent-like algorithm which could not ensure any convergence property [7]. Lin et al. presented a refined genetic algorithm (RGA) to mitigate system losses [8]. Traditional crossover and mutation strategies were adjusted through a competition mechanism in RGA. Morton and Mareels presented a brute-force solution to determine the status of each switch in order to minimize system loss in a radial distribution system [9]. The graph theory, which guarantees a global optimum yet requires an exhaustive search, was used in [9]. Wu and Tsai presented an approach based on particle swarm optimization (PSO) with an integer code to determine the switch operation schemes, which minimizes the system loss via the feeder reconfiguration in a distribution system [10]. Amanulla et al. presented a binary PSO-based algorithm to find the optimal statuses of the switches in order to maximize the reliability and minimize the real-power loss in a power system [11]. Hong and Ho proposed a Prufer-number-based genetic algorithm to reconfigure a network to ensure that the voltage drops caused by faults in voltage-sensitive areas are feasible [12]. Kavousi-Fard and Niknam proposed a self-adaptive modification method based on the clonal selection algorithm to reduce the cost of active power losses of the network and the customer interruption costs through the feeder reconfiguration [13]. Kavousi-Fard and Akbari-Zadeh used the shuffled frog leaping algorithm to reconfigure the network by considering three reliability indices and total system losses [14]. Kavousi-Fard et al. used a firefly algorithm to investigate the multiobjective probabilistic distribution feeder reconfiguration problem considering reliability [15].

The widely-installed renewable energy resources in the power system have issued new concerns regarding the feeder reconfiguration. Niknam et al. proposed a probabilistic method considering the uncertainty regarding the active and reactive load forecast errors as well as the wind-turbine output power variations concurrently to study the feeder reconfiguration. Self-adaptive modified teacher learning optimization algorithm was proposed to solve the multiobjective probabilistic problem [16]. Niknam et al. assessed the distribution feeder reconfiguration strategy, solved by a self-adaptive bat algorithm, and examined the effect of renewable energy sources on the reliability of the power system [17]. Niknam et al. proposed a two-stage approach: the roulette wheel mechanism in conjunction with the Weibull/Gaussian probability distribution functions of wind and demands were implemented to produce deterministic equivalents (scenarios); the feeder reconfiguration problem was then solved by the adaptive modified particle swarm optimization [18]. Su et al. presented a binary PSO-based method aiming at enhancing feeder configuration and reactive power control to accommodate more distributed generation resources [19]. Malekpour et al. presented an adaptive PSO algorithm to determine the optimal feeder reconfiguration while considering the uncertainty caused from the wind power generation and load demand [20]. The point estimate method was used to calculate the stochastic power flow [20]. Niknam et al. presented a honey bee mating optimization algorithm to investigate the distribution feeder reconfiguration problem while considering the effect of renewable energy sources on a system performance index [21].

Above literature survey reveals that system loss is a generally accepted performance index in the feeder reconfiguration problem. However, the above studies have the following limitations, which should be addressed in the modern smart grid:

(1)
renewable generation resources. Although they were not considered in conventional feeder reconfiguration problems [3–15], they should be considered in modern smart distribution systems;
(2)
uncertainty in renewable energies. Although uncertainty should be addressed in this area, owing to their intermittent characteristics, Kavousi-Fard and Niknam disregarded this essential factor [13, 21]. Although the uncertainty factor in renewable energies was considered in [16, 20], the point estimate method sampling two extra unsymmetrical operating points is considered to be less accurate than the Monte-Carlo simulation method [16, 20];
(3)
coordination between VAR controllers and switches. To regulate the voltage profile in the distribution system, the statuses of all switches should incorporate with VAR controllers (inverters of distributed generation resources); however, most studies have ignored this factor [2–21];
(4)
searching optimal statuses of switches: In contrast to genetic algorithms, tabu search, and other metaheuristic algorithms [3–9, 12–17, 21], PSO can search for the optimal solution efficiently. In addition to the encoding technique [10, 11, 18–20], the search approach should also be improved to make the PSO algorithm more reliable and robust.

Therefore, this work presents a novel method based on the mean-variance concept of particles (i.e., possible solutions) in PSO to determine the optimal status of each switch in the distribution system. Uncertainties in the power generation from solar PV arrays and demands are clustered to become scenarios with different weighting factors. Restated, uncertainties in the problem are transformed into scenarios. The inverters of solar PV arrays are then fully utilized to coordinate with the switches to regulate the voltage profile in order to minimize the system losses using the interior-point algorithm. More specifically, rather than stochastic power flow studies, the regulated voltages of solar PV arrays in each scenario are adjusted by the interior-point-based optimal power flow with fixed switches determined by the enhanced PSO algorithm.

The rest of this paper is organized as follows. Section 2 introduces the assumptions in the studied problem and presents the mathematical formulation of the problem. Section 3 then describes the proposed method based on fuzzy-c-means and enhanced PSO algorithm. Section 4 summarizes the simulation results. Conclusions are finally drawn in Section 5, along with recommendations for future research.

2. Assumptions and Problem Formulation

2.1. Assumptions

The following assumptions are made for the problem to avoid high voltages at the downstream customers and prevent the reverse power injected into the transmission level at the swing buses (substations).

(a)
The status of each tie switch is determined one day ahead by the preventive control using forecasted PV powers and demands with uncertainties. The voltages of inverter-based solar PV arrays are evaluated as supplemental results to support the preventive control. These inverter-controlled voltages should be recomputed in the real-time corrective control. For the preventive control, the scenarios are predetermined based on the empirical experience. No control action for the tie switch is needed once the scenarios occur. That is, a predetermined network configuration is used for many scenarios. Thus, preventive control is highly applicable to uncertainty caused from the wind powers and demands.
(b)
The inverter in either a rural field or an urban area at a bus can be considered as an aggregated one. Restated, hundreds of inverters of the solar PV arrays at a bus are operated with the same setting automatically or according to the commands of operators. Thus, a bus with large solar PV arrays is considered a voltage-controlled bus rather than a constant PQ bus.
(c)
The control center of a distribution system can communicate with the inverters through wire or wireless communication media in the demand management system (DMS) or SCADA. This assumption is applicable owing to the requirement of advanced ICT architecture in the smart distribution system.
(d)
The DC voltage of a solar PV array is boosted to a higher DC voltage, which is generally supported by a capacitor. This higher DC voltage is then modulated to a nominal AC voltage via an inverter. To achieve the voltage regulation and prevent the injection of reverse power into the transmission level (swing buses), the DC bus between the boost converter and inverter must be supported by an energy storage; the inverter must be bidirectional as well. Alternatively, a capacitor is still used for the conventionally adopted inverter, and an additional inductor is used for an appended rectifier in parallel. When the PV arrays produce (absorb) the reactive power into (from) the power system, the corresponding bus operates with a lagging (leading) power factor.

2.2. Problem Formulation

As described in Section 1, an operator has many performance indices available to determine the switch statuses. Assume that the operator attempts to minimize the real-power losses and satisfy all operational constraints. In particular, no reverse power is injected into the transmission levels. Further, assume that more than one substation (between the transmission and distribution systems) acts as swing buses in the studied problem. According to the above four assumptions, the studied problem can be formulated as follows:

()

s.t.

()

The symbols are defined as follows:

: stochastic real-power loss in the system
: vector of the stochastic real-power balance equations
: vector of the stochastic reactive power balance equations
: vector of stochastic voltage magnitudes at all buses
: vector of stochastic phase angles at all buses
: vector of stochastic real-power injections at all buses
: vector of stochastic reactive power injections at all buses
x: vector of statuses of all switches (1 or 0)
: stochastic voltage magnitude at bus n, n = 1, …, N
: stochastic line flow at line ℓ, ℓ = 1, …, L
: total stochastic power injected into substation j, j = 1,2, …, NS
: stochastic power factor at the pvth photovoltaic array, pv = 1,2, …, NP
N: number of system buses
L: number of system lines
NS: number of substations (swing buses)
NP: number of voltage controlled buses with solar PV arrays.

The values of components in x must ensure that the structure of distribution system is radial, and no islands occur in the system.

3. Proposed Method

The mathematical formulation shown in (1)–(7) incorporated with the radial and nonislanding constraints is a stochastic mixed binary programming problem. This problem has difficulty in treating stochastic equality constraints in (2) and (3) and stochastic inequality constraints in (4)–(7). Thus, by using the fuzzy-c-means (FCM), the proposed method identifies the best representative scenarios with no random variables. This work presents a novel mean-variance-based PSO algorithm to determine the statuses of switches for all scenarios. Once the status of each switch is given, the nonstochastic representative scenarios can be solved using traditional robust nonlinear programming referred to herein as interior-point algorithm. By using the “fmincon” developed in MATLAB software, this work implements the interior-point algorithm. A detailed description of “fmincon” can be found in [22], which will be neglected herein.

3.1. Fuzzy-c-Means to Identify Representative Scenarios

Both PV power generations and demands are random variables with different stochastic distributions. Theoretically, the Monte-Carlo simulation can obtain an accurate solution in case the number of sampled PV power generations and demands from their stochastic distributions is sufficiently large. However, the Monte-Carlo simulation requires a very long CPU time. If these sampled PV power generations and demands can be clustered, then the center of each cluster can serve as a representative scenario. FCM attempts to identify the representative scenarios obtained from all random variables with their individual stochastic distributions. Restated, the scenarios with real values are generated according to the stochastic distributions of all random variables (PV power generations and demands). The data sets in these scenarios are clustered using FCM. Namely, the center vector in each cluster refers to the representative scenario, and the sum of membership values in each cluster indicates the corresponding weighting factor for this representative scenario.

Bezdek et al. defined J(U, V) as an objective function in the FCM algorithm [23] as follows:

()

where C signifies the clustering number, which is determined in Section 3.2, and is fixed for in FCM. Additionally, M denotes the number of data sets generated from the Monte-Carlo simulation herein; V_c refers to the vector of the center in the cth cluster; X_i denotes the ith data vector for clustering; the membership function value μ_ci serves as a weighting factor between V_c and X_i. After the minimum of J(U, V) is gained, the M data vectors are partitioned into C clusters. Let symbols h and ε represent the iterative index and convergence tolerance, respectively. Bezdek developed the following four algorithmic steps to attain the optimum.

Step 1. Initialize a matrix of membership functions as follows:

()

where initial h equals 0.

Step 2. Let h = h + 1. Compute the center of the cth cluster as follows:

()

Step 3. Update for all X_i, i = 1, …, M.

Consider

()

Step 4. If ∥U^(h) − U^(h−1)∥ < ε, stop; otherwise, go to Step 2.

3.2. Optimal Number of Clusters

Yang and Wu proposed a partition separation (PS) validity index, in which a normalized partition coefficient is aggregated with an exponential separation measure for each cluster [24].

The PS validity index for cluster c is defined as follows:

()

where

, and

denotes the mean of all V_cs.

The PS validity index for C clusters is defined as follows:

()

A large PS(C) refers to a situation in which cluster c is compact inside and far away from other (C − 1) clusters. Consequently, the optimal number C^* (i.e., C defined in Section 3.1) of clusters can be obtained as follows:

()

3.3. Mean-Variance-Based PSO Algorithm to Determine x

As an evolutionary optimization method, PSO minimizes an objective function (performance index) by imitating the behavior of schooling fish or flocking birds [25, 26]. PSO comprises a population of particles (individuals) that represent possible solutions moving in a ψ-dimensional search space. The iterative temporary solution and updated value of a particle p are called the position and velocity, respectively. Let vectors x_p and Δx_p be the ψ-dimensional position and velocity of particle p, p = 1,2, …, P (i.e., number of population size), respectively.

The proposed method is based on the mean of the particles and standard deviation (squared root of variance) of the distances between any two particles in the tth iterations. The updated value of a particle p at iteration t is expressed as follows:

()

where the inertia weight w^t is decreased linearly from 0.5 to 0.3 because a large w^t is used for global searches, whereas local searches require a small w^t. The symbols r₁, r₂, and r₃ are random numbers within [0, 1]. Additionally,

and

are the best position of a particle in the iteration t and the best known position up to present, respectively. The learning factors a and b should meet a + b ≤ 4 [25, 26] and are defined as

()

Since the last term on the right hand side of (15) is appended, compared to the original PSO, c^t = 4 − a^t − b^t. Also,

is a ψ-dimensional vector of the mean values of all particles. The last term introduced in (15) is used to coordinate the global and local searches.

Let σ^t be the standard deviation of all distances among particles in the tth iteration. If all distances follow a Gaussian distribution, then

covers 99.7% of all particles. Let η^t = 3 − 2c^t. Because c^t in (15) decreases to zero, the values of η^t are increased to 3. This work recommends that the particles outside the distance of

in iteration t should be discarded. These discarded particles are substituted by

. Restated, if

is inside the

, then

()

is outside

, then

()

In this work, denotes the vector of statuses of all switches. All elements of are bounded to 0 or 1 through the sigmoid function. Because the number of switches with “closed” statuses is fixed (say ξ) for a distribution system to ensure a radial structure, the largest ξ elements in x are rounded to 1 and the remaining elements are reset to 0.

After the status of each switch is determined using the mean-variance-based PSO, the topology of a distribution system is fixed. Additionally, the uncertainties in wind powers and demands are modeled by many scenarios with real numbers obtained by FCM. Thus, each scenario becomes a traditional nonlinear “optimal power flow” (OPF) problem, which adjusts the inverter-controlled voltages to minimize the weighting real-power losses and meets the operational constraints, including the reverse power. The weighting factor of the objective function for each scenario c is evaluated by where the ith data set belongs to the cth cluster. In this work, the optimal power flow problem is solved using the interior-point algorithm developed in MATLAB software.

4. Simulation Results

A case study involving a 70-bus distribution system is used as an example [27], as shown in Figure 1, to show the simulation results obtained by the proposed method. Buses 1 and 70 are two substations (the swing buses). The solid lines denote the normally closed sectionalized switches, and the dot lines are normally open tie switches. Totally, the statuses of 79 switches must be determined in this work by the proposed mean-variance-based PSO.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

One-line diagram for the 70-bus distribution system.

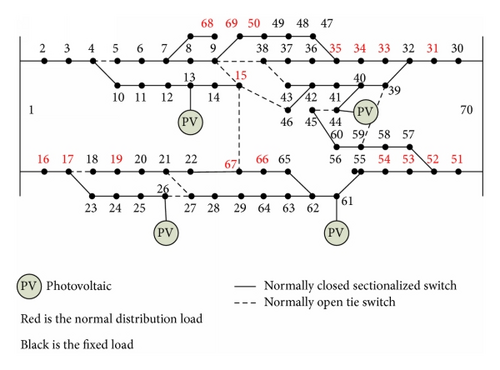
Four large solar PV arrays are installed at buses 13, 26, 44, and 61. Characteristics of the solar PV arrays are the Weibull distributions; that is, pdf (Pg) = (κ/γ)(Pg/γ)κ − 1exp⁡(−(Pg/γ)κ), where Pg denotes the PV generation. Table 1 lists the installed capacities of all PV arrays and their parameters of the Weibull distributions.

Table 1. Installed capacities of PV arrays and parameters of the Weibull distributions.

Bus	Installed capacities (kW)	Scale parameter (κ)	Shape parameter (γ)
13	750	0.35	2
26	3000	0.35	2
44	500	0.35	2
61	4500	0.35	2

In this system, the loads at 17 buses are modeled by the Gaussian distributions. They are buses 15–17, 19, 31, 33–35, 50–54, and 66–69. The mean and standard deviation of each stochastic load are 0.8 p.u. and 5% (based on its original MVA), respectively. The loads at other buses are fixed.

Three hundred sets of PV generations and loads are randomly produced using the parameters of the Weibull and Gaussian distributions, respectively; that is, M = 300, in this work. Next, by using FCM, these 300 sets of data are clustered together by considering different C. Theoretically, the maximum number of clusters is (≅17, see (14)). However, the computational burden in a PC is considered here; let the maximum number of clusters be 10. The total CPU time (C = 2,3, …, 10) to cluster these sampled PV generations and loads is 1.38 s, which was estimated by a PC with Intel Core i5 2.50 GHz and 8 GB RAM. Table 2 lists the PS validity indices for C = 2,3, …, 10. This table reveals that the optimal clustering number is 8 (i.e., C^* = 8 in (14)) because its corresponding PS validity value (3.039) is the largest.

Table 2. PS validity indices for different numbers of clusters.

C	2	3	4	5	6	7	8	9	10
PS	1.687	2.245	2.434	2.283	2.232	1.875	3.039	0.886	2.388

The 8 representative scenarios obtained by FCM were examined first by running OPF. The voltage profile and reactive powers were adjusted using 4 inverter-based solar PV at buses 13, 26, 44, and 61. Table 3 lists the 17 load buses with their representative real- and reactive-power loads (p.u.) in the 8 representative scenarios. The 4 solar PV arrays generate real power only initially with the unity power factor. This table also shows the weighting factor obtained by FCM for each scenario.

Table 3. Real and reactive powers (p.u.) and weighting factors for 8 representative scenarios (base = 1 MVA).

Bus type	Bus	Scenario
		1		2		3		4		5		6		7		8
		Real power	Reactive power	Real power	Reactive power	Real power	Reactive power	Real power	Reactive power	Real power	Reactive power	Real power	Reactive power	Real power	Reactive power	Real power	Reactive power
Load	15	0.0327	0.0204	0.0318	0.0199	0.0319	0.0199	0.0320	0.0200	0.0319	0.0199	0.0316	0.0198	0.0320	0.0200	0.0318	0.0199
	16	0.0481	0.0240	0.0474	0.0237	0.0475	0.0237	0.0481	0.0241	0.0483	0.0241	0.0472	0.0236	0.0473	0.0236	0.0484	0.0242
	17	0.0315	0.0197	0.0317	0.0198	0.0322	0.0201	0.0324	0.0203	0.0315	0.0197	0.0321	0.0200	0.0318	0.0199	0.0316	0.0198
	19	0.0103	0.0055	0.0103	0.0056	0.0104	0.0056	0.0103	0.0056	0.0105	0.0056	0.0104	0.0056	0.0102	0.0055	0.0107	0.0058
	31	0.0480	0.0320	0.0482	0.0321	0.0483	0.0322	0.0488	0.0325	0.0485	0.0323	0.0474	0.0316	0.0485	0.0323	0.0490	0.0327
	33	0.0130	0.0073	0.0126	0.0071	0.0127	0.0072	0.0130	0.0073	0.0127	0.0072	0.0128	0.0072	0.0128	0.0072	0.0129	0.0073
	34	0.0393	0.0236	0.0389	0.0234	0.0404	0.0242	0.0403	0.0242	0.0397	0.0238	0.0399	0.0240	0.0405	0.0243	0.0402	0.0241
	35	0.0323	0.0226	0.0322	0.0225	0.0316	0.0221	0.0321	0.0225	0.0322	0.0225	0.0320	0.0224	0.0320	0.0224	0.0315	0.0221
	50	0.1142	0.0734	0.1108	0.0712	0.1130	0.0727	0.1131	0.0727	0.1111	0.0714	0.1121	0.0720	0.1127	0.0724	0.1097	0.0705
	51	0.0469	0.0312	0.0481	0.0321	0.0486	0.0324	0.0477	0.0318	0.0480	0.0320	0.0476	0.0318	0.0481	0.0321	0.0475	0.0317
	52	0.0161	0.0088	0.0162	0.0089	0.0162	0.0089	0.0159	0.0088	0.0158	0.0087	0.0158	0.0087	0.0161	0.0088	0.0160	0.0088
	53	0.0322	0.0242	0.0319	0.0239	0.0317	0.0238	0.0322	0.0241	0.0321	0.0241	0.0317	0.0238	0.0319	0.0239	0.0322	0.0242
	54	0.0288	0.0192	0.0284	0.0190	0.0291	0.0194	0.0288	0.0192	0.0283	0.0189	0.0288	0.0192	0.0289	0.0193	0.0287	0.0191
	66	0.1229	0.1065	0.1195	0.1035	0.1222	0.1059	0.1185	0.1027	0.1198	0.1038	0.1204	0.1044	0.1196	0.1037	0.1191	0.1033
	67	0.0199	0.0119	0.0200	0.0120	0.0201	0.0121	0.0196	0.0118	0.0201	0.0120	0.0202	0.0121	0.0201	0.0121	0.0201	0.0121
	68	0.0802	0.0481	0.0785	0.0471	0.0800	0.0480	0.0788	0.0473	0.0792	0.0475	0.0815	0.0489	0.0765	0.0459	0.0800	0.0480
	69	0.0322	0.0242	0.0319	0.0239	0.0316	0.0237	0.0319	0.0239	0.0324	0.0243	0.0317	0.0238	0.0318	0.0238	0.0320	0.0240

PV	13	0.1462	—	0.2480	—	0.1091	—	0.1096	—	0.1484	—	0.0731	—	0.1937	—	0.0753	—
	26	0.4785	—	0.4285	—	0.5024	—	0.4038	—	0.7548	—	0.3558	—	0.9308	—	0.8790	—
	44	0.1734	—	0.0757	—	0.0451	—	0.1171	—	0.0658	—	0.0734	—	0.1018	—	0.1412	—
	61	1.2912	—	0.7270	—	0.5237	—	0.4600	—	1.4779	—	1.1095	—	0.5398	—	0.8762	—
Weighting factor		0.0855		0.1532		0.1646		0.1653		0.1194		0.1308		0.0923		0.0887

First, the interior-point-based OPF was used to regulate the voltage profile and minimize the system losses individually for these 8 scenarios. Table 4 summarizes the optimal results before the feeder reconfiguration. This table reveals that a reverse power −95.092 kW was injected into bus 1 in scenario 7. There is also reverse reactive power (−361.796 kVAr) at bus 26. The other scenarios had no reverse power at buses 1 and 70.

Table 4. Optimal results before feeder reconfiguration.

Scenario	1	2	3	4	5	6	7	8
Voltage magnitude (p.u.)
V₁	1.041	1.043	1.039	1.045	1.026	1.047	0.974	1.019
V₁₃	1.021	1.034	1.015	1.021	1.006	1.020	0.950	0.991
V₂₆	1.050	1.050	1.050	1.050	1.050	1.050	0.984	1.050
V₄₄	1.015	1.010	1.008	1.012	1.006	1.009	1.024	1.014
V₆₁	1.049	1.000	0.980	0.974	1.050	1.035	1.009	1.014
V₇₀	1.050	1.050	1.050	1.050	1.047	1.050	1.050	1.050
Reactive power (kVAr)
Q₁₃	109.684	185.963	81.792	82.203	111.297	54.847	0.002	56.510
Q₂₆	207.808	209.497	206.809	206.289	209.705	204.487	−361.796	207.732
Q₄₄	130.072	56.783	33.835	87.807	49.377	55.037	502.178	105.918
Q₆₁	941.614	545.250	392.784	345.034	819.679	832.136	954.342	657.163
Real power at swing bus (kW)
P₁	361.171	304.607	375.732	473.122	91.277	557.162	−95.092	50.501
P₇₀	1953.526	2640.701	2912.282	2902.069	1877.819	2241.501	2800.633	2410.641
Total load (kW)	4286.679	4276.304	4285.446	4281.481	4280.026	4281.264	4278.722	4279.626
Loss (kW)	117.429	148.208	182.827	184.226	135.961	129.235	193.034	153.292
Aggregating loss = 157.874 kW

By using the proposed method, the statuses of 79 switches were determined using the mean-variance-based PSO; the voltage profile was also regulated using the interior-point-based OPF. The population size was 10, and the inertia was decreased linearly from 0.5 to 0.3 in 100 iterations in the proposed PSO algorithm. Table 5 lists the optimal solutions obtained by the proposed method. The injection powers −95.092 (bus 1) and 2,800.633 kW (bus 70) before feeder reconfiguration were changed to 702.954 (bus 1) and 1,893.876 kW (bus 70) after feeder reconfiguration in scenario 7, respectively. The system losses were also reduced from 157.874 to 92.875 kW. The proposed method required 11,835.41 CPU seconds to attain the optimal solution. Figure 2 shows the optimal feeder reconfiguration using the proposed method.

Table 5. Optimal results after the feeder reconfiguration using the proposed method.

Scenario	1	2	3	4	5	6	7	8
Voltage magnitude (p.u.)
V₁	1.050	1.050	1.050	1.050	1.046	1.050	1.037	1.040
V₁₃	1.013	1.024	1.008	1.009	1.009	1.004	1.004	0.994
V₂₆	1.036	1.032	1.038	1.030	1.050	1.026	1.050	1.050
V₄₄	0.994	1.014	1.012	1.016	0.978	0.998	1.015	1.014
V₆₁	1.050	1.047	1.029	1.023	1.050	1.050	1.030	1.050
V₇₀	1.025	1.050	1.050	1.050	1.016	1.035	1.050	1.046
Reactive power (kVAr)
Q₁₃	109.686	185.963	81.792	82.204	111.298	54.847	145.300	56.510
Q₂₆	358.888	321.407	376.783	302.842	415.400	266.856	419.470	411.446
Q₄₄	130.073	56.783	33.835	87.807	49.378	55.037	76.380	105.918
Q₆₁	541.639	545.250	392.784	345.034	532.708	530.894	404.858	532.886
Real power at swing bus (kW)
P₁	1209.57	1149.71	1223.55	1324.58	928.005	1415.21	702.954	885.934
P₇₀	1081.67	1726.06	1974.25	1959.51	1016.86	1356.16	1893.88	1508.39
Loss (kW)	93.979	78.674	92.627	93.126	111.735	101.945	84.322	86.471
Aggregating loss = 92.875 kW

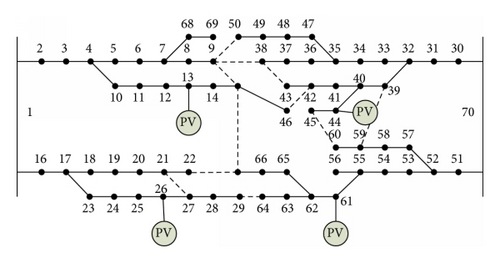
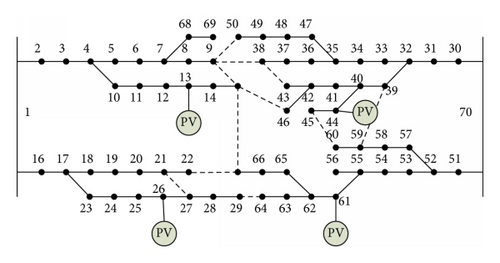
Table 6 shows the optimal solutions gained by using chaos-based PSO and GA. The results gained by chaos-based PSO and GA are the same. The numerical parameters used in the chaos-based PSO are the same as those in the proposed method. The crossover and mutation rates in GA are 0.8 and 1/790, respectively. The merits of the proposed method are as follows. (a) The CPU times required by chaos-based PSO (15,224.55 s) and GA (18,508.64 s) are much longer than that (11,835.41 s) required in the proposed method. (b) The aggregating loss attained by the proposed method is 92.875 kW, which is smaller than 93.738 kW obtained by both chaos-based PSO and GA. Figure 3 illustrates the optimal feeder reconfiguration obtained by the chaos-based PSO and GA algorithms.

Table 6. Optimal results after feeder reconfiguration using chaos-based PSO and GA.

Scenario	1	2	3	4	5	6	7	8
Voltage magnitude (p.u.)
V₁	1.050	1.050	1.050	1.050	1.046	1.050	1.037	1.040
V₁₃	1.019	1.030	1.015	1.015	1.015	1.011	1.011	1.000
V₂₆	1.036	1.032	1.038	1.030	1.050	1.026	1.050	1.050
V₄₄	0.992	1.011	1.009	1.014	0.976	0.995	1.013	1.011
V₆₁	1.050	1.047	1.029	1.023	1.050	1.050	1.030	1.050
V₇₀	1.026	1.050	1.050	1.050	1.017	1.035	1.050	1.046
Reactive power (kVAr)
Q₁₃	109.686	185.963	81.792	82.204	111.298	54.847	145.300	56.510
Q₂₆	358.889	321.407	376.783	302.842	418.678	266.856	422.320	415.772
Q₄₄	130.073	56.783	33.835	87.807	49.378	55.037	76.380	105.918
Q₆₁	536.509	545.250	392.784	345.034	526.576	525.289	404.859	528.011
Real power at swing bus (kW)
P₁	1145.56	1087.05	1159.05	1260.09	864.00	1350.20	639.51	820.838
P₇₀	1146.37	1791.07	2039.45	2024.28	1082.32	1421.35	1958.74	1573.05
Loss (kW)	94.658	81.017	93.310	93.400	113.189	102.117	85.737	86.035
Aggregating loss = 93.738 kW

5. Conclusions

This work presents a novel method that incorporates FCM, partition separation validity index, mean-variance-based PSO, and interior-point-based optimal power flow to conduct feeder reconfiguration in order to prevent the revere power caused by uncertain solar PV arrays from injecting into the transmission level. The novelties are as follows: (a) the uncertainty in the PV powers and demands is modeled by multiple scenarios gained by FCM in order to avoid probabilistic calculations; (b) the novel mean-variance-based PSO implements an adaptive elite strategy that replaces the particles far away from with . The number of replacement decreases according to the standard deviation of distances among particles. Simulation results demonstrate that the proposed method is faster than the chaos-based PSO method. Furthermore, the proposed method can solve the problem with the reverse power and high voltage at the customers’ side while minimizing the system loss.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

The authors would like thank the National Science Council of the Republic of China, Taiwan, for financially supporting this research under Contract no. NSC103-3113-P-008-001. Ted Knoy is appreciated for his editorial assistance.

References

1 Kyoto Protocol to the United Nations—framework convention on climate change, December 1997.
Google Scholar
2 The Copenhagen Accord, United Nations Climate Change Conference, December 2009.
Google Scholar
3 Brano V. L., Ciulla G., and Falco M. D., Artificial neural networks to predict the power output of a PV panel, International Journal of Photoenergy. (2014) 2014, 12, https://doi.org/10.1155/2014/193083, 193083.
10.1155/2014/193083
Google Scholar
4 Engin M., Sizing and simulation of PV-wind hybrid power system, International Journal of Photoenergy. (2013) 2013, 10, https://doi.org/10.1155/2013/217526, 217526.
10.1155/2013/217526
Web of Science® Google Scholar
5 Chao K. H., Chang L. Y., and Liu H. C., Maximum power point tracking method based on modified particle swarm optimization for photovoltaic systems, International Journal of Photoenergy. (2013) 2013, 6, https://doi.org/10.1155/2013/583163, 583163.
10.1155/2013/583163
Web of Science® Google Scholar
6 Mahamudul H., Saad M., and Henk M. I., Photovoltaic system modeling with fuzzy logic based maximum power point tracking algorithm, International Journal of Photoenergy. (2013) 2013, 10, https://doi.org/10.1155/2013/762946, 762946.
10.1155/2013/762946
Google Scholar
7 Jeon Y. J. and Kim J. C., Network reconfiguration in radial distribution system using simulated annealing and tabu search, IEEE PES Winter Meeting, January 2000, 23–27.
Google Scholar
8 Lin W.-M., Cheng F.-S., and Tsay M.-T., Distribution feeder reconfiguration with refined genetic algorithm, IEE Proceedings: Generation, Transmission and Distribution. (2000) 147, no. 6, 349–354, 2-s2.0-0034314279, https://doi.org/10.1049/ip-gtd:20000715.
Google Scholar
9 Morton A. B. and Mareels I. M. Y., An efficient brute-force solution to the network reconfiguration problem, IEEE Transactions on Power Delivery. (2000) 15, no. 3, 996–1000, 2-s2.0-0034223728, https://doi.org/10.1109/61.871365.
Google Scholar
10 Wu W.-C. and Tsai M.-S., Application of enhanced integer coded particle swarm optimization for distribution system feeder reconfiguration, IEEE Transactions on Power Systems. (2011) 26, no. 3, 1591–1599, 2-s2.0-79960890301, https://doi.org/10.1109/TPWRS.2010.2094212.
Google Scholar
11 Amanulla B., Chakrabarti S., and Singh S. N., Reconfiguration of power distribution systems considering reliability and power loss, IEEE Transactions on Power Delivery. (2012) 27, no. 2, 918–926, 2-s2.0-84859776329, https://doi.org/10.1109/TPWRD.2011.2179950.
Google Scholar
12 Hong Y.-Y. and Ho S.-Y., Determination of network configuration considering multiobjective in distribution systems using genetic algorithms, IEEE Transactions on Power Systems. (2005) 20, no. 2, 1062–1069, 2-s2.0-18944391892, https://doi.org/10.1109/TPWRS.2005.846067.
Google Scholar
13 Kavousi-Fard A. and Niknam T., Optimal distribution feeder reconfiguration for reliability improvement considering uncertainty, to appear in IEEE Transactions on Power Delivery.
Google Scholar
14 Kavousi-Fard A. and Akbari-Zadeh M. R., Reliability enhancement using optimal distribution feeder reconfiguration, Neurocomputing. (2013) 106, 1–11.
Google Scholar
15 Kavousi-Fard A., Niknam T., and Bazia A., A novel multi-objective self-adaptive modified firefly algorithm for optimal operation management of stochastic DFR strategy, International Transactions on Electrical Energy Systems. (2014) https://doi.org/10.1002/etep.1881.
Google Scholar
16 Niknam T., Kavousi Fard A., and Baziar A., Multi-objective stochastic distribution feeder reconfiguration problem considering hydrogen and thermal energy production by fuel cell power plants, Energy. (2014) 55, 680–691, 2-s2.0-84859459757, https://doi.org/10.1016/j.energy.2012.02.023.
Google Scholar
17 Niknam T., Kavousi Fard A., and Baziar A., Multi-objective stochastic distribution feeder reconfiguration problem considering hydrogen and thermal energy production by fuel cell power plants, Energy. (2014) 64, 342–354, 2-s2.0-84859459757, https://doi.org/10.1016/j.energy.2012.02.023.
Google Scholar
18 Niknam T., Kavousifard A., and Aghaei J., Scenario-based multiobjective distribution feeder reconfiguration considering wind power using adaptive modified PSO, IET Renewable. (2012) 6, no. 4, 236–247.
Google Scholar
19 Su S.-Y., Lu C.-N., Chang R.-F., and Gutiérrez-Alcaraz G., Distributed generation interconnection planning: a wind power case study, IEEE Transactions on Smart Grid. (2011) 2, no. 1, 169–177, 2-s2.0-79951883876, https://doi.org/10.1109/TSG.2011.2105895.
Google Scholar
20 Malekpour A. R., Niknam T., Pahwa A., and Kavousi-Fard A., Multi-objective stochastic distribution feeder reconfiguration in systems with wind power generators and fuel cells using the point estimate method, IEEE Transactions on Power Systems. (2013) 28, no. 2, 1483–1492.
Google Scholar
21 Niknam T., Fard A. K., and Seifi A., Distribution feeder reconfiguration considering fuel cell/wind/photovoltaic power plants, Renewable Energy. (2012) 37, no. 1, 213–225, 2-s2.0-79961125921, https://doi.org/10.1016/j.renene.2011.06.017.
Google Scholar
22 Optimization Toolbox-Fmincon, MATLAB, the MathWorks, 2009.
Google Scholar
23 Bezdek J. C., Ehrlich R., and Full W., FCM: the fuzzy c-means clustering algorithm, Computers and Geosciences. (1984) 10, no. 2-3, 191–203, 2-s2.0-0021583718.
Google Scholar
24 Yang M.-S. and Wu K.-L., A new validity index for fuzzy clustering, Proceedings of the 10th IEEE International Conference on Fuzzy Systems, December 2001, Melbourne, Australia, 89–92, 2-s2.0-0035747063.
Google Scholar
25 Kennedy J. and Eberhart R., Swarm Intelligence, 2001, Morgan Kaufmann Publishers, Elsevier, San Francisco, Calif, USA.
Google Scholar
26 Eberhart R. and Kennedy J., New optimizer using particle swarm theory, Proceedings of the 6th International Symposium on Micro Machine and Human Science, October 1995, 39–43, 2-s2.0-0029517385.
Google Scholar
27 Malekpour A. R. and Niknam T., A probabilistic multi-objective daily Volt/Var control at distribution networks including renewable energy sources, Energy. (2011) 36, no. 5, 3477–3488, 2-s2.0-79955661132, https://doi.org/10.1016/j.energy.2011.03.052.
Google Scholar

Citing Literature

All articles

Enhanced Particle Swarm Optimization-Based Feeder Reconfiguration Considering Uncertain Large Photovoltaic Powers and Demands

Abstract

1. Introduction