International Journal of Computational Mathematics
Volume 2014, Issue 1 631749
Research Article
Open Access

Computational Modelling of Couette Flow of Nanofluids with Viscous Heating and Convective Cooling

Oluwole Daniel Makinde, 

Oluwole Daniel Makinde

Faculty of Military Science, Stellenbosch University, Private Bag X2, Saldanha 7395, South Africa sun.ac.za

Search for more papers by this author
Ahmada Omar, 

Corresponding Author

Ahmada Omar

Mathematics and Computational Science and Engineering, Nelson Mandela African Institution of Science and Technology (NM-AIST), Arusha, Tanzania nm-aist.ac.tz

Search for more papers by this author
M. Samuel Tshehla, 

M. Samuel Tshehla

Faculty of Military Science, Stellenbosch University, Private Bag X2, Saldanha 7395, South Africa sun.ac.za

Search for more papers by this author
First published: 14 December 2014
https://doi.org/10.1155/2014/631749
Citations: 4
Academic Editor: Zhijie Xu

Abstract

The combined effect of viscous heating and convective cooling on Couette flow and heat transfer characteristics of water base nanofluids containing Copper Oxide (CuO) and Alumina (Al2O3) as nanoparticles is investigated. It is assumed that the nanofluid flows in a channel between two parallel plates with the channel’s upper plate accelerating and exchange heat with the ambient surrounding following the Newton’s law of cooling, while the lower plate is stationary and maintained at a constant temperature. Using appropriate similarity transformation, the governing Navier-Stokes and the energy equations are reduced to a set of nonlinear ordinary differential equations. These equations are solved analytically by regular perturbation method with series improvement technique and numerically by an efficient Runge-Kutta-Fehlberg integration technique coupled with shooting method. The effects of the governing parameters on the dimensionless velocity, temperature, skin friction, pressure drop and Nusselt number are presented graphically, and discussed quantitatively.

1. Introduction

Studies related to laminar flow and heat transfer of a viscous fluid in the space between two parallel plates, one of which is moving relative to the other, have received the attention of several researchers due to their numerous industrial and engineering applications. This type of flow is named in honour of Maurice Marie Alfred Couette, a professor of physics at the French University of Angers in the late 19th century [1]. Couette flow has been used to estimate the drag force in many wall driven applications such as lubrication engineering, power generators and pumps, polymer technology, petroleum industry, and purification of crude oil. Literature survey indicates that interest in the Couette flows has grown during the past decades. Jana and Datta [2] examined the effects of Coriolis force on the Couette flow and heat transfer between two parallel plates in a rotating system. Singh [3] studied unsteady free convection flow of an incompressible viscous fluid between two vertical parallel plates, in which one is fixed and the other is impulsively started in its own plane. Kearsley [4] investigated the problem of steady state Couette flow with viscous heating. Jha [5] numerically examined the effects of magnetic field on Couette flow between two vertical parallel plates. The combined effects of variable viscosity and thermal conductivity on generalized Couette flow and heat transfer in the presence of transversely imposed magnetic field have been studied numerically by Makinde and Onyejekwe [6]. Seth et al. [7] presented a closed form solution for hydromagnetic unsteady Couette flow of a viscous incompressible electrically conducting fluid between two parallel porous plates. Deka and Bhattacharya [8] obtained an exact solution of unsteady free convective Couette flow of a viscous incompressible heat generating/absorbing fluid confined between two vertical plates in a porous medium. Meanwhile, the enhancement of heat transfer in a Couette flow of fluid subjected to a temperature gradient is an important issue that is expected to improve the efficient operation of several engineering and tribological devices. Other relevant applications can be found in engine cooling, solar water heating, cooling of electronics, cooling of transformer oil, improving diesel generator efficiency, cooling of heat exchanging devices, improving heat transfer efficiency of chillers, domestic refrigerator-freezers, and cooling in machining and in nuclear reactor. The common heat transfer fluids such as water, ethylene glycol, and engine oil have limited heat transfer capabilities owing to their low thermal conductivity whereas metals have much higher thermal conductivities than these fluids. With the recent improvements in nanotechnology, the production of particles with sizes on the order of nanometers can be achieved. Consequently, the idea of dispersing these nanoparticles in a base liquid for improving thermal conductivity has been proposed [9]. Such suspension of nanoparticles in a base fluid is called a nanofluid. Due to their small size, nanoparticles fluidize easily inside the base fluid, and as a consequence, clogging of channels and erosion in channel walls are no longer a problem. It is even possible to use nanofluids in microchannels [10]. Niu et al. [11] theoretically studied the slip-flow and heat transfer of a non-Newtonian nanofluid in a microtube by means of theoretical method. In their research, the power-law rheology was adopted to describe the non-Newtonian characteristics of the flow, in which the fluid consistency coefficient and the flow behaviour index depend on the nanoparticle volume fraction. Motsumi and Makinde [12] reported a numerical solution for the effects of thermal radiation and viscous dissipation on boundary layer flow of nanofluids over a permeable moving flat plate. Choi et al. [13] studied the Couette flow of nanofluids composed of negatively charged nanoparticles dispersed in aqueous NaCl solutions. They found that the velocity profile of nanofluids containing charged nanoparticles deviates significantly from the classical linear velocity profile of Couette flow.

In the studies mentioned above, the combined effects of viscous heating and convective cooling on Couette flow of nanofluids have not been discussed while such flows are very important in lubrication technology and tribological problems. Therefore, the objective of the present paper is to analyze the effects of viscous heating and convective cooling on the Couette flow of water base nanofluids containing Copper Oxide (CuO) and Alumina (Al2O3) as nanoparticles. In Sections 2–4, the model nonlinear governing equations together with the analytical and numerical solution are obtained. Pertinent results are presented graphically and discussed quantitatively in Section 5 while the conclusions are drawn in Section 6.

2. Problem Formulation

We consider a two-dimensional steady Couette flow of viscous incompressible water base nanofluids containing Copper Oxide (CuO) and Alumina (Al2O3) as nanoparticles in which an accelerating upper plate drags adjacent fluid along with it and thereby imparts a motion to the rest of the fluid. The lower plate is fixed and kept at a constant temperature T0 while the upper accelerating plate is subjected to a convective heat exchange with the ambient surrounding following Newton’s law of cooling. We choose a Cartesian coordinates system in such a way that the x-axis is taken along the channel and the y-axis is normal to it as shown in Figure 1.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Schematic diagram of the physical system.
The governing equations which are those of conservation of mass, momentum, and energy are [1, 4, 13]
()
()
()
()
where (u, v) are the velocity components of the nanofluid in the (x, y) directions, respectively, E is the upper plate acceleration parameter, a is the channel width, P is the pressure, T is the nanofluid temperature, μnf is the Maxwell-Garnetts [14] approximation for effective dynamic viscosity of the nanofluid, knf is the effective thermal conductivity of the nanofluid given by Brinkman [15], ρnf is the nanofluid density, and (ρcp) nf is the heat capacitance of the nanofluid which are given by [16, 17]
()
In (5), φ is the nanoparticles solid volume fraction, ρf is the reference density of the fluid fraction, ρs is the reference density of the solid fraction, μf is the viscosity of the fluid fraction, kf is the thermal conductivity of the fluid fraction, cp is the specific heat at constant pressure, and ks is the thermal conductivity of the solid volume fraction. The boundary conditions at the channel walls may be written as
()
where Ta is the ambient surrounding temperature and h is the coefficient of heat transfer. Introducing the stream function ψ and vorticity Ω into the governing equations (1)–(4) we have the following:
()
After eliminating the pressure P from (2) and (3), we obtain
()
()
The following dimensionless variables and parameters are introduced into (8) and (9) together with their corresponding boundary conditions,
()
and we obtain
()
with
()
where R is the Reynolds number, Ec is the Eckert number, Bi is the Biot number, Pr⁡ is the base fluid Prandtl number, and m1, m2, m3, and m4 can be easily determined from the thermophysical properties of the base fluid and the nanoparticles. We seek a similarity form of solution of the form:
()
Substituting (13) into (11)-(12), we obtain
()
()
()
()
()
The dimensionless fluid axial pressure gradient is given as
()
where
()
Other quantities of practical interest in this study are the local skin friction coefficient Cf and the local Nusselt number Nu, which are defined as
()
where τw is the skin friction and qw is the heat flux at the channel upper accelerating wall which are given by
()
Using (10) and (13), we substitute (22) into (21) and obtain
()
In the following section, the boundary value problems in (14)–(18) were solved analytically using regular perturbation method and numerically by the Runge-Kutta-Fehlberg method with shooting technique [18]. The results are utilised to compute the fluid pressure gradient, local skin friction, and local Nusselt number as highlighted in (20) and (23).

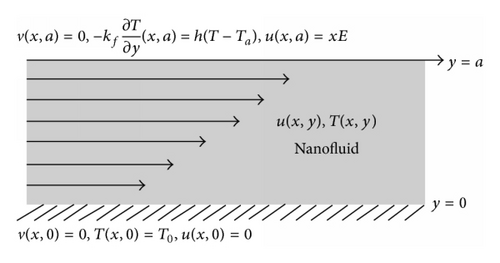
3. Perturbation Method

The governing model equations (14)–(18) are nonlinear and this makes its exact solution very intractable. However, approximate solution can be easily obtained by forming a power series expansion in the parameter R. It is worth noting that an exact solution may exist for this problem under certain assumptions. The existence of exact solution provides remarkable and more accurate results. Assume a series solution of the form:
()
Substituting the solution series in (24) into (14)–(18) and collecting the coefficients of like powers of R, we obtain the following.
Zeroth Order. Consider
()
with
()
Higher Order (n ≥ 1). Consider
()
with
()
The equations are solved iteratively and the series solutions for the velocity and temperature fields are given as
()
where the expressions for Gi, i = 1,2, 3, are given in the appendix. Using a computer symbolic algebra package (MAPLE), several terms of the above solution series in (29) are obtained. From (29) together with (20) and (23), we obtained the series solutions for the skin friction, Nusselt number, and axial pressure gradient as
()
The expressions for N and M are given in the appendix. These power series solutions are valid for very small parameter values of R, however, using Padé approximation technique [19] that is based on the series summation and improvement method; the usability of the solution series is extended beyond small parameter values of R.

4. Numerical Procedure

Here, we employed Runge-Kutta-Fehlberg method with shooting technique [18] to numerically solve the coupled nonlinear ordinary differential equations (14)–(16) subject to the boundary conditions (17)-(18) for different set of parameter values. The procedure involves transforming the nonlinear boundary value problem (BVP) into an initial value problem (IVP) as follows: let
()
Equation (31) is substituted into (14)–(18) and a system of first order differential equations is obtained:
()
subject to the initial conditions
()
To determine the unspecified initial conditions s1, s2, s3, and s4 in (33), the initial guesses are supplied and resulting IVP is solved using Runge-Kutta scheme. The process is repeated until the solution at η = 1 shoots to the boundary conditions at that point. The best way to achieve this is to supply the initial condition in to the Runge-Kutta scheme as unknown and solve the resulting nonlinear algebraic system of equations iteratively using Newton-Raphson. It is important to note that the resulting nonlinear system of algebraic equation may not have unique solution; therefore a carefully chosen initial guess which is close to the desired solution must be supplied. The scheme has quadratic convergence with step size taken as Δη = 0.001 and tolerance set to 10−7.

5. Results and Discussion

The Couette flow and heat transfer characteristics of water base nanofluids containing CuO and Al2O3 as nanoparticles with viscous heating and convective cooling have been investigated. The nonlinear similarity ordinary differential equations governing the boundary value problem were solved both analytically using the perturbation method coupled with series improvement technique and numerically using Runge-Kutta-Fehlberg integration technique coupled with shooting scheme. Thermophysical properties of base fluid and nanoparticles are presented in Table 1. For pure water, the Prandtl number is taken as Pr⁡ = 6.2 [12, 16, 17] and momentum diffusivity is dominant within the fluid in comparison to pure conduction. The nanoparticle volume fraction in the base fluid is taken as φ = 0 to 0.3 (i.e., ranging from 0 to 30 percent) while the case of φ = 0 corresponds to the absence of nanoparticle in the based fluid (water). Numerical solutions are displayed in Tables 2 and 3 together with Figures 2–17. In Tables 2 and 3, the numerical values of the skin friction and the Nusselt number are displayed when R = 1 for both the series solution and the numerical solution with increasing nanoparticle volume fraction. It is noteworthy that perfect agreement is achieved between the improved series solution and the numerical solution. Moreover, it is observed that both the skin friction and the Nusselt number increase with increasing nanoparticles volume fraction. Interestingly, the skin friction produced by Al2O3-water nanofluid is higher than that of CuO-water nanofluid while Nusselt number produced by CuO-water nanofluid is higher than that of Al2O3-water nanofluid.

Table 1. Thermophysical properties of the fluid phase (water) and nanoparticles [16, 17].
Physical properties

Fluid phase

(water)

 CuO Al2O3
cp (J/kgK) 4179 6500 765
ρ (kg/m3) 997.1 535.6 3970
k (W/mK) 0.613 20 40
Table 2. Computation showing the skin friction for R = 1, X = 1.
φ

Cf 

CuO-water

(series)

Cf 

CuO-water

(numerical)

Cf 

Al2O3-water

(series)

Cf 

Al2O3-water

(numerical)
0.00 4.085563 4.0855627 4.085563 4.0855627
0.01 4.186948 4.1869479 4.189890 4.1898897
0.05 4.630877 4.6308766 4.645589 4.6455887
0.10 5.287037 5.2870375 5.316469 5.3164695
0.15 6.084673 6.0846727 6.128833 6.1288327
0.20 7.065422 7.0654222 7.124319 7.1243186
0.25 8.286944 8.2869436 8.360585 8.3605848
0.30 9.830736 9.8307360 9.919130 9.9191299
Table 3. Computation showing the Nusselt number for Bi = 1, R = 1, Ec = 0.1, and X = 1.
φ

Nu

CuO-water

(series)

Nu

CuO-water

(numerical)

Nu

Al2O3-water

(series)

Nu

Al2O3-water

(numerical)
0.00 0.315380 0.3153802 0.315380 0.3153802
0.01 0.326419 0.3264199 0.326493 0.3264928
0.05 0.376286 0.3762861 0.376626 0.3766263
0.10 0.452718 0.4527175 0.453179 0.4531794
0.15 0.547443 0.5474432 0.547555 0.5475550
0.20 0.664319 0.6643189 0.663318 0.6633184
0.25 0.808605 0.8086051 0.805338 0.8053384
0.30 0.987501 0.9875014 0.980249 0.9802487
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Nanofluids velocity profiles.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Axial velocity profiles with increasing φ.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Axial velocity profiles with increasing R.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Nanofluids temperature profiles.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Temperature profiles with increasing φ.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Temperature profiles with increasing Ec.
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Temperature profiles with increasing X.
Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
Temperature profiles with increasing Bi.
Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
Temperature profiles with increasing R.
Details are in the caption following the image
Figure 11
Open in figure viewerPowerPoint
Skin friction with increasing φ.
Details are in the caption following the image
Figure 12
Open in figure viewerPowerPoint
Skin friction with increasing R.
Details are in the caption following the image
Figure 13
Open in figure viewerPowerPoint
Axial pressure gradient with increasing φ.
Details are in the caption following the image
Figure 14
Open in figure viewerPowerPoint
Axial pressure gradient with increasing R.
Details are in the caption following the image
Figure 15
Open in figure viewerPowerPoint
Nusselt number with increasing φ.
Details are in the caption following the image
Figure 16
Open in figure viewerPowerPoint
Nusselt number with increasing Ec, R, and Bi.
Details are in the caption following the image
Figure 17
Open in figure viewerPowerPoint
Nusselt number with increasing X.

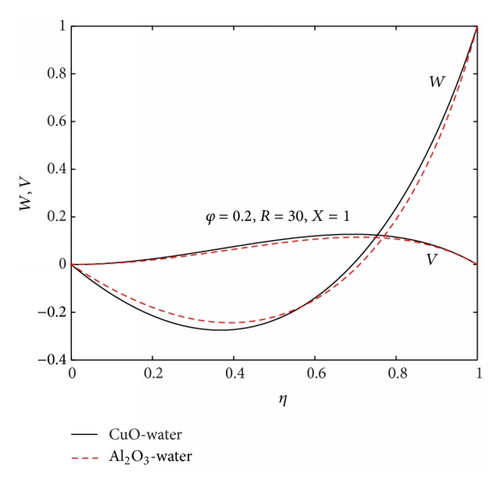
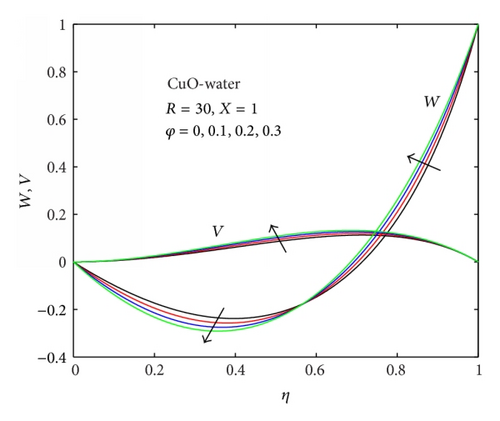
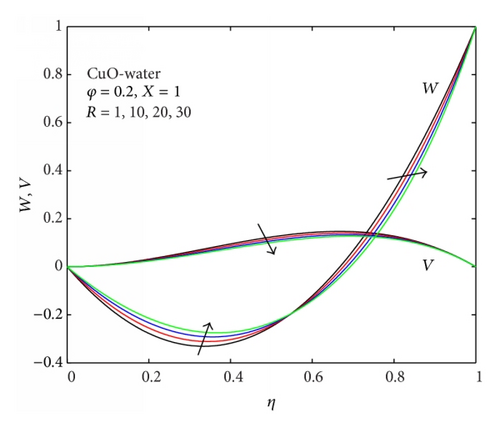
5.1. Velocity Profiles with Parameter Variation

Figures 2–4 illustrate the effects of parameter variation on both the axial and normal velocity profiles. Generally, flow reversal is observed in the region near the lower fixed plate as represented by negative value of the axial velocity (W) while the fluid near the upper accelerating plate moves faster forward in the axial direction. Also the normal velocity profiles (V) are skewed towards the upper plate due to the drag force exerted on the fluid by the upper plate acceleration. Figure 2 shows that the intensity of flow reversal near the lower fixed plate and the skewness of the normal velocity towards the upper moving plate produced by CuO-water are higher than that of Al2O3-water under the same parametric conditions. With CuO-water as the working nanofluid, it is observed that increasing nanoparticles volume fraction concentration from 0 to 30% increases the flow reversal near the lower fixed plate and the skewness of the normal velocity towards the upper moving plate as shown in Figure 3. With increasing acceleration of the upper plate (i.e., R increasing), a decrease in the flow reversal near the lower fixed plate and the skewness of the normal velocity towards the upper plate is observed as depicted in Figure 4. This decrease in flow reversal can be attributed to an increase in the drag force exerted on the fluid by the upper plate. The intersection of the velocities W and V at a region near the upper moving plate as shown in Figures 2, 3, and 4 indicates that both the axial and the normal velocities of nanofluids at this point (i.e., between eta = 0.75 and 0.78) are the same. This implies that the axial acceleration of the upper plate may not have any noticeable influence on both W and V velocities at this intersecting region.

5.2. Temperature Profiles with Parameter Variation

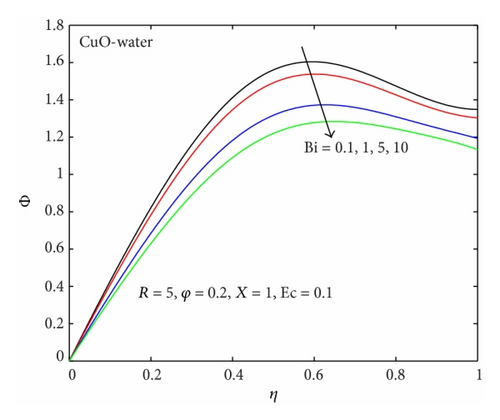
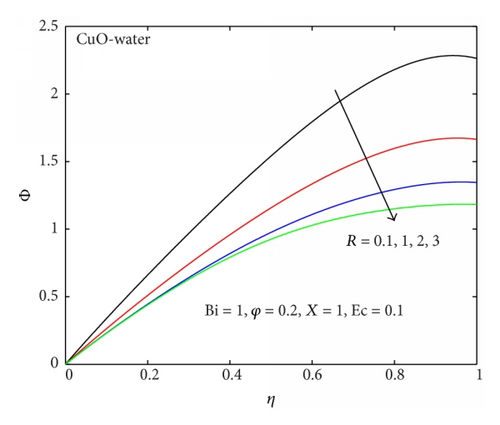
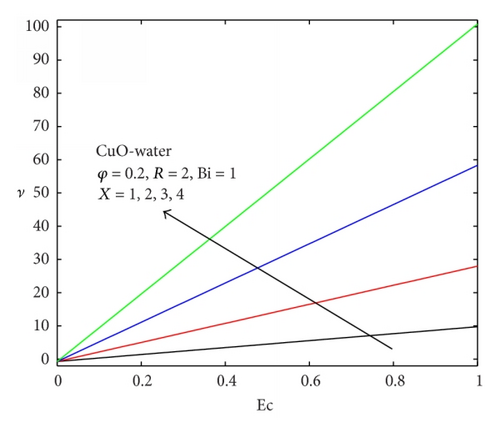
The temperature profiles of the nanofluids with different parameter variation are displayed in Figures 5–10. Generally, the fluid temperature increases within the channel and decreases near the upper moving plate due to convective heat loss to ambient surrounding. It is noteworthy that the temperature produced by CuO-water nanofluid is generally higher than that of Al2O3-water nanofluid under the same flow condition as shown in Figure 5. With CuO-water as the working nanofluid, the temperature increases with a rise in nanoparticles volume fraction from 0 to 30% as illustrated in Figure 6. Similar effect of an increase in nanofluid temperature is observed in Figures 7 and 8 with an increase in Ec due to viscous dissipation and axial distance along the channel. This may be attributed to the fact that as Ec increases, the internal heat generation within the fluid due velocity gradient increases, leading to a rise in temperature. The axial increase in temperature may be justified by the quadratic expression in axial distance for fluid temperature in (16) (i.e., Φ(X, η) = H(η) + X2θ(η)). Figures 9 and 10 show that the nanofluid temperature decreases with increasing Biot number (Bi) and upper plate acceleration (R). This is expected, since an increase in Biot number indicates a rise in convective cooling due to heat loss to the ambient surrounding from the upper plate. Moreover, an increase in the upper plate acceleration also enhanced convective heat loss; consequently, the nanofluid temperature decreases.

5.3. Skin Friction, Pressure Gradient, and Nusselt Number

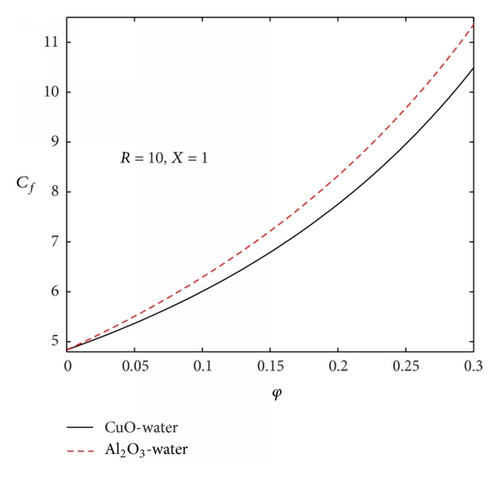
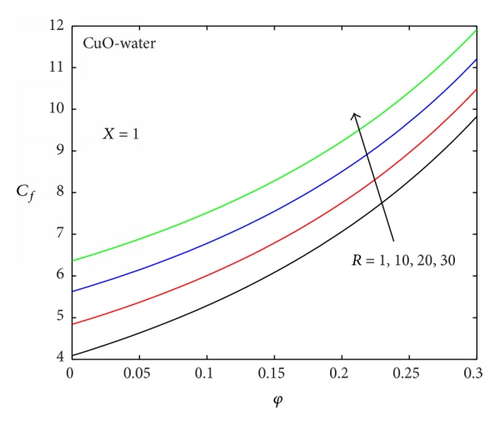
Figures 11 and 12 depict the skin friction profiles for both CuO-water and Al2O3-water nanofluids at the upper moving plate. The skin friction generally increases with an increase in nanoparticles volume fraction; however, it is noticed that the skin friction produced by Al2O3-water is more intense than the one produced by CuO-water as shown in Figure 11. This is expected since the axial velocity gradient of Al2O3-water at the upper moving plate is higher than that of CuO-water. With CuO-water as the working nanofluid, it is observed that the skin friction increases with an increase in upper plate acceleration as indicated by increasing values of R in Figure 12. The pressure drop along the channel is illustrated in Figures 13 and 14. For both CuO-water and Al2O3-water nanofluids, it is seen in Figure 13 that the pressure drop increases with increasing nanoparticles volume fraction and CuO-water produced higher pressure drop as compared to Al2O3-water. With CuO-water as the working nanofluid, an increase in the upper plate acceleration causes a decrease in pressure drop as shown in Figure 14. Figures 15–17 illustrate the effects of parameter variation on the rate of heat transfer at the moving upper plate. For both nanofluids, the Nusselt number increases with an increase in nanoparticles volume fraction and the Nusselt number produced by CuO-water nanofluid is higher than that of Al2O3-water nanofluid (see Figure 15). In Figures 16 and 17, it is observed that the strength of the upper plate heat transfer rate is enhanced with increasing axial distance, viscous dissipation, and convective cooling. This may be attributed to a rise in the temperature gradient due to convective heat exchange with the ambient along the upper plate. However, a decrease in the Nusselt number is observed with increasing upper plate acceleration. The closeness of the profiles for the Nusselt number values in Figure 15 with small increase in nanoparticles volume fraction shows that at very small values of nanoparticles volume fraction (φ < 0.12) the rate of heat transfer across the upper moving plate surface for both nanofluids is the same; however, as the nanoparticles volume fraction increases, the CuO-water produces higher heat transfer rate as compared to Al2O3-water.

6. Conclusions

We analysed the combined effects of viscous dissipation and convective cooling on Couette flow and heat transfer of water base nanofluids containing CuO and Al2O3 as nanoparticles. The nonlinear boundary value problem is solved using both perturbation series improvement method and Runge-Kutta-Fehlberg integration numerical technique coupled with shooting scheme. The summary of essential features of physical interest from the above analysis is given below.

The flow reversal near the lower fixed plate and the skewness of the normal velocity towards the upper moving plate produced by CuO-water are higher than that of Al2O3-water which increases with φ and decreases with R. CuO-water produced higher temperature as compared to Al2O3-water. The temperature increases with φ, Ec, and X but decreases with Bi and R. The coefficient of skin friction increases with R and φ while Nusselt number increases with increasing φ, Ec, Bi, and X and decreases with R. Moreover, Al2O3-water produced higher skin friction while CuO-water produced higher Nusselt number. The pressure drop produced by CuO-water is higher than that of Al2O3-water and it is enhanced by φ but decreases with R.

Nomenclature

  • (u, v):
  • Velocity components
  • (x, y):
  • Coordinates
  • knf:
  • Nanofluid thermal conductivity
  • Pr⁡:
  • Prandtl number
  • Bi:
  • Local Biot number
  • Ta:
  • Ambient temperature
  • F:
  • Dimensionless stream function
  • T0:
  • Lower wall temperature
  • T:
  • Temperature
  • H:
  • Dimensionless temperature
  • R:
  • Reynolds number
  • cp:
  • Specific heat at constant pressure
  • ks:
  • Solid fraction thermal conductivity
  • kf:
  • Base fluid thermal conductivity
  • W:
  • Dimensionless axial velocity
  • V:
  • Dimensionless normal velocity
  • Ec:
  • Eckert number
  • E:
  • Upper wall acceleration parameter
  • X:
  • Dimensionless axial coordinate
  • A:
  • Axial pressure gradient coefficient
  • a:
  • Channel width
  • Nu:
  • Nusselt number
  • Cf:
  • Skin friction coefficient.
  • Greek Symbols
  •  
  • ψ:
  • Stream function
  • θ:
  • Dimensionless temperature
  • μnf:
  • Nanofluid dynamic viscosity
  • αnf:
  • Nanofluid thermal diffusivity
  • η:
  • Dimensionless normal coordinate
  • ρnf:
  • Nanofluid density
  • ρs:
  • Solid fraction density
  • υf:
  • Base fluid kinematic viscosity
  • μf:
  • Base fluid dynamic viscosity
  • φ:
  • Solid volume fraction parameter
  • ρf:
  • Base fluid density
  • Ω:
  • Vorticity
  • :
  • Dimensionless stream function
  • :
  • Dimensionless vorticity
  • Φ:
  • Dimensionless temperature.

    • Conflict of Interests

    The authors declare that there is no conflict of interests regarding the publication of this paper.

    Acknowledgments

    The authors wish to express their sincere thanks to anonymous reviewers for their valuable suggestions and comments.

      Appendix

      Consider
      ()

        The full text of this article hosted at iucr.org is unavailable due to technical difficulties.