Representing and Counting the Subgroups of the Group
Abstract
We deduce a simple representation and the invariant factor decompositions of the subgroups of the group , where m and n are arbitrary positive integers. We obtain formulas for the total number of subgroups and the number of subgroups of a given order.
1. Introduction
Let be the group of residue classes modulo m and consider the direct product , where m and n are arbitrary positive integers. This paper aims to deduce a simple representation and the invariant factor decompositions of the subgroups of the group G. As consequences we derive formulas for the number of certain types of subgroups of G, including the total number s(m, n) of its subgroups and the number sk(m, n) of its subgroups of order k (k∣mn).
Subgroups of (sublattices of the two-dimensional integer lattice) and associated counting functions were considered by several authors in pure and applied mathematics. It is known, for example, that the number of subgroups of index n in is σ(n), the sum of the (positive) divisors of n. See, for example, [1, 2], [3, item A001615]. Although features of the subgroups of G not only are interesting by their own but also have applications, one of them is described below, it seems that a synthesis on subgroups of G cannot be found in the literature.
In the case m = n, the subgroups of play an important role in numerical harmonic analysis, more specifically in the field of applied time-frequency analysis. Time-frequency analysis attempts to investigate function behavior via a phase space representation given by the short-time Fourier transform [4]. The short-time Fourier coefficients of a function f are given by inner products with translated modulations (or time-frequency shifts) of a prototype function g, assumed to be well localized in phase space, for example, a Gaussian. In applications, the phase space corresponding to discrete, finite functions (or vectors) belonging to is exactly . Concerned with the question of reconstruction from samples of short-time Fourier transforms, it has been found that when sampling on lattices, that is, subgroups of , the associated analysis and reconstruction operators are particularly rich in structure, which, in turn, can be exploited for efficient implementation (cf. [5–7] and references therein). It is of particular interest to find subgroups in a certain range of cardinality; therefore, a complete characterization of these groups helps choose the best one for the desired application.
We recall that a finite Abelian group of order >1 has rank r if it is isomorphic to , where and nj∣nj+1 (1 ≤ j ≤ r − 1), which is the invariant factor decomposition of the given group. Here the number r is uniquely determined and represents the minimal number of generators of the group. For general accounts on finite Abelian groups see, for example, [8, 9].
Formula (3) was derived by Călugăreanu [12, Section 4] and recently by Petrillo [13, Proposition 2] using Goursat’s lemma for groups. Tărnăuceanu [14, Proposition 2.9] and [15, Theorem 3.3] deduced (3) and (4) by a method based on properties of certain attached matrices.
Therefore, s(m, n) and sk(m, n) can be computed using (1), (3) and (2), (4), respectively. We deduce other formulas for s(m, n) and sk(m, n) (Theorems 3 and 4), which generalize (3) and (4) and put them in more compact forms. These are consequences of a simple representation of the subgroups of , given in Theorem 1. This representation might be known, but the only source we could find is the paper [5], where only a special case is treated in a different form. More exactly, in [5, Lemma 4.1] a representation for lattices in of redundancy 2, that is, subgroups of having index n/2, is given, using matrices in Hermite normal form. Theorem 2 gives the invariant factor decompositions of the subgroups of G. We also consider the number of cyclic subgroups of (Theorem 5) and the number of subgroups of a given exponent in (Theorem 8).
Our approach is elementary, using only simple group-theoretic and number-theoretic arguments. The proofs are given in Section 4.
Throughout the paper we use the following notations: , , τ(n) and σ(n) are the number and the sum, respectively, of the positive divisors of n, ψ(n) = n∏p∣n (1 + 1/p) is the Dedekind function, ω(n) stands for the number of distinct prime factors of n, μ is the Möbius function, ϕ denotes Euler’s totient function, and ζ is the Riemann zeta function.
2. Subgroups of
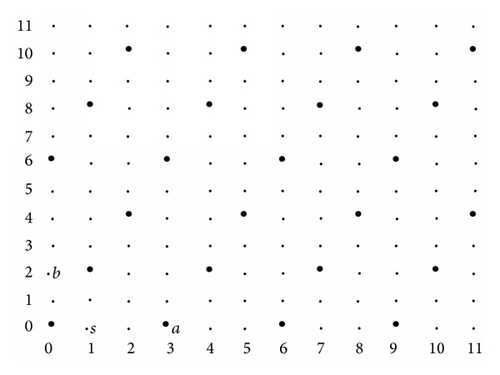
The subgroups of can be identified and visualized in the plane with sublattices of the lattice . Every two-dimensional sublattice is generated by two basis vectors. For example, Figure 1 shows the subgroup of having the basis vectors (3,0) and (1,2).
This suggests the following representation of the subgroups.
Theorem 1. For every , let
Then Ha,b,t is a subgroup of order mn/ab of and the map (a, b, t) ↦ Ha,b,t is a bijection between the set Im,n and the set of subgroups of .
This notation for s will be used also in the rest of the paper. Note also that in the case a ≠ m, b ≠ n the area of the parallelogram spanned by the basis vectors is ab, exactly the index of Ha,b,t.
We say that a subgroup H = Ha,b,t is a subproduct of if H = H1 × H2, where H1 and H2 are subgroups of and , respectively.
Theorem 2. (i) The invariant factor decomposition of the subgroup Ha,b,t is given by
(ii) The exponent of the subgroup Ha,b,t is β.
(iii) The subgroup Ha,b,t is cyclic if and only if α = 1.
(iv) The subgroup Ha,b,t is a subproduct if and only if t = 0 and . Here Ha,b,0 is cyclic if and only if gcd(m/a, n/b) = 1.
For example, for the subgroup represented by Figure 1 one has m = n = 12, a = 3, b = 2, s = 1, α = 2, and β = 12, and this subgroup is isomorphic to . It is not cyclic and is not a subproduct.
According to Theorem 1, the number s(m, n) of subgroups of can be obtained by counting the elements of the set Im,n. We deduce the following.
Theorem 3. For every , s(m, n) is given by
Formula (10) is a special case of a formula representing the number of all subgroups of a class of groups formed as cyclic extensions of cyclic groups, deduced by Calhoun [16] and having a laborious proof. Note that formula (10) is given, without proof in [3, item A054584].
Note also that the function (m, n) ↦ s(m, n) is representing a multiplicative arithmetic function of two variables; that is, s(mm′, nn′) = s(m, n)s(m′, n′) holds for any such that gcd(mn, m′n′) = 1. This property, which is in concordance with (1), is a direct consequence of formula (10). See Section 5.
Let N(a, b, c) denote the number of solutions of the system of equations xy = a, zt = b, xz = c.
Theorem 4. For every , such that k∣mn,
The identities (3) and (4) can be easily deduced from each of the identities given in Theorems 3 and 4, respectively.
Theorem 5. Let .
(i) The number c(m, n) of cyclic subgroups of is given by
(ii) The number of subproducts of is τ(m)τ(n) and the number of its cyclic subproducts is τ(mn).
Formula (17), as a special case of an identity valid for arbitrary finite Abelian groups, was derived by the third author [17, 18] using different arguments. The function (m, n) ↦ c(m, n) is also multiplicative.
3. Subgroups of
In the case m = n, which is of special interest in applications, the results given in the previous section can be easily used. We point out that n ↦ s(n): = s(n, n) and n ↦ c(n): = c(n, n) are multiplicative arithmetic functions of a single variable (sequences [3, items A060724, A060648]). They can be written in the form of Dirichlet convolutions as shown by the next corollaries.
Corollary 6. For every ,
Corollary 7. For every ,
Theorem 8. For every with δ∣n, the number of subgroups of exponent δ of equals the number of cyclic subgroups of .
4. Proofs
Proof of Theorem 1. Let H be a subgroup of . Consider the natural projection given by π2(x, y) = y. Then π2(H) is a subgroup of and there is a unique divisor b of n such that π2(H) = 〈b〉: = {jb : 0 ≤ j ≤ n/b − 1}. Let s ≥ 0 be minimal such that (s, b) ∈ H.
Furthermore, consider the natural inclusion given by ι1(x) = (x, 0). Then is a subgroup of and there exists a unique divisor a of m such that .
We show that . Indeed, for every , (ia + js, jb) = i(a, 0) + j(s, b) ∈ H. On the other hand, for every (u, v) ∈ H one has v ∈ π2(H) and hence there is such that v = jb. We obtain (u − js, 0) = (u, v) − j(s, b) ∈ H, and there is with u − js = ia.
Here a necessary condition is that (sn/b, 0) ∈ H (obtained for i = 0 and j = n/b), that is, a∣sn/b, equivalent to a/gcd(a, n/b)∣s. Clearly, if this is verified, then for the above representation of H it is enough to take the values 0 ≤ i ≤ m/a − 1 and 0 ≤ j ≤ n/b − 1.
Also, dividing s by a we have s = aq + r with 0 ≤ r < a and (r, b) = (s, b) − q(a, 0) ∈ H, showing that s < a, by its minimality. Hence s = ta/gcd(a, n/b) with 0 ≤ t ≤ gcd(a, n/b) − 1. Thus we obtain the given representation.
Conversely, every (a, b, t) ∈ Im,n generates a subgroup Ha,b,t of order mn/(ab) of and the proof is complete.
Proof of Theorem 2. (i)-(ii) We first determine the exponent of the subgroup Ha,b,t. Ha,b,t is generated by (a, 0) and (s, b); hence, its exponent is the least common multiple of the orders of these two elements. The order of (a, 0) is m/a. To compute the order of (s, b) note that m∣rs if and only if m/gcd(m, s)∣r. Thus the order of (s, b) is lcm(m/gcd(m, s), n/b). We deduce that the exponent of Ha,b,t is
For every finite Abelian group the rank of a nontrivial subgroup is at most the rank of the group. Therefore, the rank of Ha,b,t is 1 or 2. That is, with certain such that A∣B. Here the exponent of Ha,b,t equals that of , which is lcm(A, B) = B. Using (ii) already proved we deduce that B = β. Since the order of Ha,b,t is AB = mn/(ab) we have A = mn/(abβ) = α.
(iii) According to (i), where α∣β. Hence Ha,b,t is cyclic if and only if α = 1.
(iv) The subgroups of are of form {ia : 0 ≤ i ≤ m/a − 1}, where a∣m, and the properties follow from (6) and (iii).
Proof of Theorem 3. By its definition, the number of elements of the set Im,n is
To obtain formula (11) apply the Gauss formula n = ∑d∣n ϕ(d) () by writing the following:
Now (12) follows from (11) by the Busche-Ramanujan identity (cf. [19, Chapter 1]):
Proof of Theorem 4. According to Theorem 1,
Proof of Theorem 5. (i) According to Theorems 1 and 2/(iii) and using that ∑d∣n μ(d) = 1 or 0 and according to n = 1 or n > 1,
Now regrouping the terms according to ei = z and be = t we obtain
The next results follow applying Gauss’ formula and the Busche-Ramanujan formula, similar to the proof of Theorem 3.
(ii) For the subproducts Ha,b,0 the values a∣m and b∣n can be chosen arbitrary and it follows at once that the number of subproducts is τ(m)τ(n). The number of cyclic subproducts is
5. Further Remarks
- (1)
As mentioned in Section 2 the functions (m, n) ↦ s(m, n) and (m, n) ↦ c(m, n) are multiplicative functions of two variables. This follows easily from formulae (10) and (17), respectively. Namely, according to those formulae s(m, n) and c(m, n) are two variables Dirichlet convolutions of the functions (m, n) ↦ gcd(m, n) and (m, n) ↦ ϕ(gcd(m, n)), respectively, with the constant 1 function, all multiplicative. Since convolution preserves the multiplicativity we deduce that s(m, n) and c(m, n) are also multiplicative. See [17, Section 2] for details.
- (2)
Asymptotic formulas with sharp error terms for the sums ∑m,n≤x s(m, n) and ∑m,n≤x c(m, n) were given in the paper [20].
- (3)
For any finite groups A and B a subgroup C of A × B is cyclic if and only if and have coprime orders, where ι1 and ι2 are the natural inclusions ([21, Theorem 4.2]). In the case , , and C = Ha,b,t one has and and the characterization of the cyclic subgroups Ha,b,t given in Theorem 2/(iii) can be obtained also in this way. It turns out that regarding the sublattice, Ha,b,t is cyclic if and only if the numbers of points on the horizontal and vertical axes, respectively, are relatively prime. Note that in the case m = n the above condition reads ngcd(a, b, s) = ab. Thus it is necessary that n∣ab. The subgroup on Figure 1 is not cyclic.
- (4)
Note also the next formula for the number of cyclic subgroups of , derived in [22, Example 2]:
() -
where the sum is over all ordered pairs (d, e) such that lcm(d, e) = n. For a short direct proof of (40) write , with gcd(a, b) = 1. Then , , and obtain
() -
according to (21).
- (5)
Every subgroup K of has the representation , where 0 ≤ s ≤ a and 0 ≤ b are unique integers. This follows like in the proof of Theorem 1. Furthermore, in the case a, b ≥ 1, 0 ≤ s ≤ a − 1 the index of K is ab and one obtains at once that the number of subgroups K having index n () is ∑ab=n ∑0≤s≤a−1 1 = ∑ab=n a = σ(n), mentioned in Section 1.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Acknowledgments
Nicki Holighaus was partially supported by the Austrian Science Fund (FWF) START-Project FLAME (Y551-N13). László Tóth gratefully acknowledges support from the Austrian Science Fund (FWF) under Project no. M1376-N18. Christoph Wiesmeyr was partially supported by EU FET Open Grant UNLocX (255931).




