International Journal of Partial Differential Equations
Volume 2014, Issue 1 461046
Research Article
Open Access

Semilinear Evolution Problems with Ventcel-Type Conditions on Fractal Boundaries

Maria Rosaria Lancia, 

Corresponding Author

Maria Rosaria Lancia

Dipartimento di Scienze di Base e Applicate per l′Ingegneria, Università degli Studi di Roma “La Sapienza”, Via A. Scarpa 16, 00161 Roma, Italy uniroma1.it

Search for more papers by this author
Paola Vernole, 

Paola Vernole

Dipartimento di Matematica, Università degli Studi di Roma “La Sapienza”, Piazzle Aldo Moro 2, 00185 Roma, Italy uniroma1.it

Search for more papers by this author
First published: 22 January 2014
https://doi.org/10.1155/2014/461046
Citations: 1
Academic Editor: William E. Fitzgibbon

Abstract

A semilinear parabolic transmission problem with Ventcel′s boundary conditions on a fractal interface S or the corresponding prefractal interface Sh is studied. Regularity results for the solution in both cases are proved. The asymptotic behaviour of the solutions of the approximating problems to the solution of limit fractal problem is analyzed.

1. Introduction

In this paper we study the parabolic semilinear second-order transmission problem which we formally state as
(1)
where Q is the bounded open set (−1,1) 2 × (0,1), and L is a “cylindrical” layer dividing the set Q into two subsets Q1 and Q2 (see Figure 2). When L is the Koch-type surface S = K × I, where K is the snowflake and I = [0,1] (see Section 2), EL is the energy functional ES introduced in (12); when L is the prefractal surface Sh, EL is the energy functional introduced in (24). J is a nonlinear function from a subset of L2(Q) into L2(Q). ui denotes the restriction of u to Qi, [u] = u1 − u2 denotes the jump of u across L, ΔL denotes the Laplace operator defined on the layer L (see (12) in Section 3), and [∂u/∂n] = ∂u1/∂n1 + ∂u2/∂n2 denotes the jump of the normal derivatives across L, to be intended in a suitable sense.

More precisely, we assume that J(u) is a nonlinear mapping from L2p(Q) to L2(Q) for any fixed p > 1, locally Lipschitz; that is, Lipschitz on bounded sets in L2p(Q) with Lipschitz constant l(r) when restricted to B(0, r) ⊂ L2p(Q), satisfying suitable growth conditions (see conditions (i) and (ii) in Section 4). Examples of this type of nonlinearity include, for example, J(u) = u | u|p−1,  p > 1 which occur in combustion theory (see [1]) and in the Navier-Stokes system (see [2]).

In the recent years there has been an increasing interest in the study of linear transmission problems across irregular layers of fractal type and the corresponding prefractal layers [3–7]. Problems of this type are also known in the literature as problems with Ventcel’s boundary conditions [8] or second-order transmission conditions. Fractal layers can provide new interesting settings in those model problems, in which the surface absorption of tension, electric conduction, or flow is the relevant effect. The literature on semilinear equations on smooth domains is extensive (see e.g., [9–13] and the recent review in [14]); the fractal case is more awkward (see e.g., [15–19]).

In our case one has to take into account that the diffusion phenomenon takes place both across the smooth domain Q and the cylindrical layer L; this fact has a counterpart in the structure of the energy functional E[u] and hence on problem . In [18] the authors proved local existence and uniqueness results of the “mild” solution of an abstract evolution transmission problem across a prefractal or fractal interface (see (36) and (37)).

In this paper we give a strong interpretation of the abstract problem studied in [18],;namely, we prove that the solution of the abstract problem solves problem in a suitable sense (see Theorems 22 and 20).

The results on the strong interpretation in the prefractal case are deduced by proving regularity results for the solutions of elliptic problems in polyhedral domains. It turns out that the restriction of the solution uh to belongs to suitable weighted Sobolev spaces (see the proof of Theorem 22). This regularity result is important not only in itself but also in the numerical approximation procedure; to this regard, see [20]. Following this point of view, it is also important to study the asymptotic behaviour of the solutions of the prefractal problems.

The proof of the convergence of the solution of the prefractal problems to the one of the (limit) fractal problem relies on the convergence, in the Mosco’s sense, of the energy forms which, in turn, implies the convergence of semigroups in the strong operator topology of L2(Q) (see Theorem 16). The plan of the paper is as follows. In Section 2 we describe the geometry of the problem; in Section 3 we introduce the Dirichlet energy forms and the associated semigroups and we recall the results on the convergence of the approximating energy forms (see [21] for details). In Section 4 we recall existence and uniqueness results for the local mild solution as well as global existence and regularity results. In Section 5 we prove that the solution of the abstract Cauchy problems (P) and (Ph) solves problem in the fractal and prefractal cases, respectively, (see Theorems 22 and 20). In Section 6 we prove the convergence of the solutions of the approximating problems to the solution of the limit fractal problem in a suitable functional space. In Appendices A and B, for the reader convenience, we introduce the functional spaces and traces involved.

2. Geometry of the Fractal Layers S and Sh

In the paper by |P − P0| we denote the Euclidean distance in ℝD and the Euclidean balls by B(P0, r) = {P ∈ ℝD:|P − P0 | < r},  P0 ∈ ℝD,  r > 0. By the Koch snowflake F, we will denote the union of three coplanar Koch curves (see [22]) K1, K2, and K3 as shown in Figure 1. We assume that the junction points A1, A3, and A5 are the vertices of a regular triangle with unit side length; that is, |A1 − A3 | = |A1 − A5 | = |A3 − A5 | = 1. In this section we briefly recall the essential notions on the geometry; for details see [18].

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Decomposition of the snowflake.
Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Two different viewpoints of the domain Q and the layer S.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Two different viewpoints of the domain Q and the layer S.

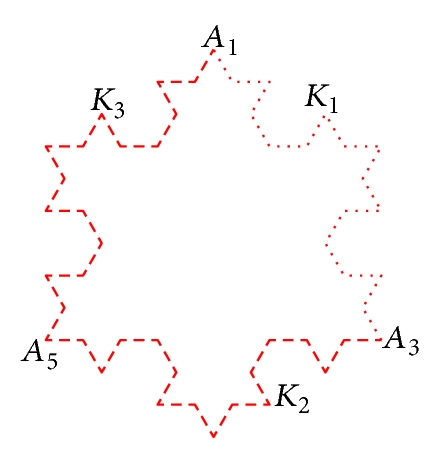
The Hausdorff dimension of the Koch snowflake is given by df = log⁡⁡4/log⁡⁡3. This fractal is no longer self-similar (and hence not nested).

One can define, in a natural way, a finite Borel measure μF supported on F by
(2)
where μi denotes the normalized df-dimensional Hausdorff measure, restricted to Ki, i = 1,2, 3.
The measure μF has the property that there exist two positive constants c1 and c2:
(3)
where d = df = log⁡⁡4/log⁡⁡3 and B(P, r) denotes the Euclidean ball in ℝ2. As μF is supported on F, it is not ambiguous to write in (3) μF(B(P, r)) in place of μF(B(P, r)∩F). In the terminology of Appendices A and B, we say that F is a d-set with d = df.

Remark 1. The Koch snowflake can be also regarded as a fractal manifold (see [23] Section  2.2).

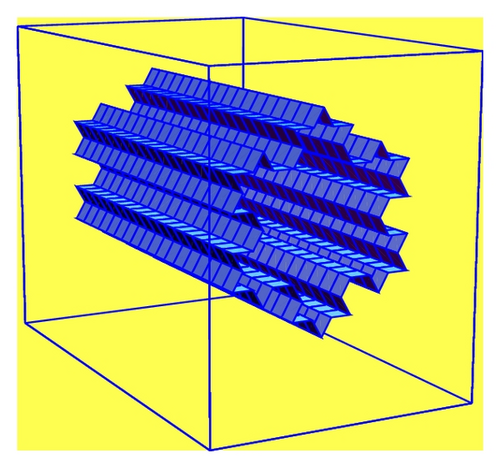
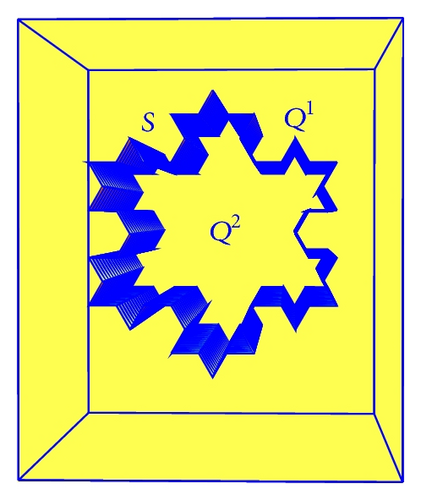
Let Q denote a bounded open set in ℝ3; in our basic model, Q denotes the parallelepiped Q = (−1,1) 2 × (0,1) and S denotes a “cylindrical” layer in Q of the type S = F × I, where I = [0,1] and F is the Koch snowflake. We assume that S is located in a median position inside Q and divides Q in two subsets Q1 and Q2 (see Figure 2).

We give a point P ∈ S the Cartesian coordinates P = (x, y), where x = (x1, x2) are the coordinates of the orthogonal projection of P on the plane containing F and y is the coordinate of the orthogonal projection of P on the y-line containing the interval I: P = (x, y) ∈ S, x = (x1, x2) ∈ F, y ∈ I.

One can define, in a natural way, a finite Borel measure m supported on S as the product measure
(4)
where dy denotes the one-dimensional Lebesgue measure on I. The measure m has the property that there exist two positive constants c1 and c2:
(5)
where d = df + 1 = log⁡⁡12/log⁡⁡3 and B(P, r) denotes the Euclidean ball in ℝ3. As m is supported on S, it is not ambiguous to write in (5) m(B(P, r)) in place of m(B(P, r)∩S). Thus S turns out to be a d-set with d = df + 1 (see Appendices A and B).

By Sh, we denote the prefractal layer of the type Sh = Fh × I, h = 1,2, …, Fh is the piecewise linear prefractal approximation of F at the step h. Sh is a surface of polyhedral type. Sh divides Q in two subsets ,  i = 1,2.

We give a point P ∈ Sh the Cartesian coordinates P = (x, y), where x = (x1, x2) are the coordinates of the orthogonal projection of P on the plane containing Fh and y is the coordinate of the orthogonal projection P on the y-line containing the interval I.

3. Energy Forms and Semigroups Associated

3.1. The Energy Form E

In this section we introduce the energy functional on S. We first define the energy functional on the cross section F by integrating its Lagrangian on F. For the concept of Lagrangian on fractals, that is, the notion of a measure-valued local energy, we refer to [24, 25]. Here for the sake of simplicity we only mention that the Lagrangian on K, ℒK, is a measure-valued map on 𝒟(F) × 𝒟(F) which is bilinear symmetric and positive (ℒK[u] is a positive measure.) The measure-valued Lagrangian takes on the fractal K the role of the Euclidean Lagrangian dℒ(u, v) = ∇u · ∇vdx. Note that in the case of the Koch curve, the Lagrangian is absolutely continuous with respect to the measure μ; on the contrary, this is not true on most fractals (see [24]). In [23] the Lagrangian ℒF on the snowflake F has been defined by using its representation as a fractal manifold. Here we do not give details on the construction and definition of ℒF and we refer to Section  4 in [23] for details; in particular in Definition 4.5 a Lagrangian measure ℒF on F and the corresponding energy form ℰF as
(6)
with domain 𝒟(F) have been introduced. The domain 𝒟(F), which is a Hilbert space with norm
(7)
has been characterized in terms of the domains of the energy forms on Ki (see [23] Theorem 4.6).

In the following, we will omit the subscript F, the Lagrangian measure will be simply denoted by ℒ(u, v), and we will set ℒ[u] = ℒ(u, u); an analogous notation will be adopted for the energies.

We define the energy forms ES on the fractal layer S = F × I by setting
(8)
where σ1 and σ2 are positive constants. Here ℒx(·, ·)(dx) denotes the measure-valued Lagrangian (of the energy form ℰF of F with domain 𝒟(F)) now acting on u(x, y) and v(x, y) as function of x ∈ F for a.e. y ∈ I; μF(dx) is the df-Hausdorff measure acting on each section F of S for a.e. y ∈ I with df = log⁡⁡4/log⁡⁡3; Dy(·) denotes the derivative in the y direction.
The form ES is defined for u ∈ 𝒟(S), where 𝒟(S) is the closure in the intrinsic norm
(9)
of the set
(10)
where L2(F) = L2(F, μF(dx)).
In the following, we will also use the form ES(u, v) which is obtained from ES[u] by the polarization identity:
(11)

Proposition 2. In the previous notations and assumptions, the form ES with domain 𝒟(S) is a regular Dirichlet form in L2(S, m) and the space 𝒟(S) is a Hilbert space under the intrinsic norm (9).

The proof can be carried on as in Proposition 3.1 of [26]. For the definition and properties of regular Dirichlet forms, we refer to [25]. We now define the Laplace operator on S. As (ES, 𝒟(S)) is a closed, bilinear form on L2(S, m), there exists (see Chapter 6, Theorem  2.1 in [27]) a unique self-adjoint, nonpositive operator ΔS on L2(S, m)—with domain 𝒟(ΔS)⊆𝒟(S) dense in L2(S, m)—such that
(12)
Let (𝒟(S))′ denote the dual of the space 𝒟(S). We now introduce the Laplace operator on the fractal S as a variational operator from 𝒟(S) → (𝒟(S))′ by
(13)
for z ∈ 𝒟(S) and for all w ∈ 𝒟(S), where is the duality pairing between (𝒟(S))′ and 𝒟(S). We use the same symbol ΔS to define the Laplace operator both as a self-adjoint operator in (12) and as a variational operator in (13). It will be clear from the context to which case we refer.

In the next, we will also use the spectral dimension ν of S. We find that if r(λ) is the number of eigenvalues associated with ES smaller than λ, then r(λ) ~ λν/2. It can be shown that in our case ν = 2 (see [28, 29]). We stress the fact that in the fractal case ν < d < D, while in the Euclidean setting ν = d.

Consider now the space of functions u : Q → ℝ as
(14)
Here we denote by the symbol f|S the trace γ0f of f to S (see Appendices A and B).
The space V(Q, S) is nontrivial; see Proposition 3.3 of [4]. We now introduce the energy form
(15)
defined on the domain V(Q, S). Here and in the following, dQ denotes the 3-dimensional Lesbesgue measure and E(u, v) denotes the corresponding bilinear form
(16)
defined on V(Q, S) × V(Q, S).

As in Theorem 3.2 of [26], the following result can be proved.

Proposition 3. The form E defined in (15) is a regular Dirichlet form in L2(Q) and the space V(Q, S) is a Hilbert space equipped with the scalar product

(17)

We denote by ∥u∥V(Q,S) the norm in V(Q, S), associated with (17), that is
(18)
As in Propositions (3.6) and (3.1) in [4], the following result can be proved.

Proposition 4. The space 𝒟(S) is embedded in .

Proposition 5. The space 𝒟(S) is embedded in , α < 1.

As (E, V(Q, S)) is a closed bilinear form on L2(Q) with domain V(Q, S) dense in L2(Q), there exists (see Chapter 6 Theorem  2.1 in [27]) a unique self-adjoint nonpositive operator A on L2(Q) with domain 𝒟(A)⊆V(Q, S) dense in L2(Q) such that
(19)
Moreover in Theorem 13.1 of [25] it is proved that to each closed symmetric form E a family of linear operators {Gα, α > 0} can be associated with the property
(20)
and this family is a strongly continuous resolvent with generator A, which also generates a strongly continuous semigroup {T(t)} t≥0.

For the reader’s convenience, we recall here the main properties of the semigroup {T(t)} t≥0; the reader is referred to Proposition  3.5 in [21] for the proof.

Proposition 6. Let {T(t)} t≥0 be the semigroup generated by the operator A associated with the energy form in (19). Then {T(t)} t≥0 is an analytic contraction positive preserving semigroup in L2(Q).

Remark 7. It is well known that the symmetric and contraction analytic semigroup T(t) uniquely determines analytic semigroups on the space Lp, 1 ≤ p < ∞ (see Theorem 1.4.1 [30]) which we still denote by T(t) and by Ap its infinitesimal generator.

From Theorem  2.11 in [31], the following estimate on the decay of the heat semigroup holds.

Proposition 8. There exists a positive constant M such that

(21)
One will consider the case n = 3 and ν = 2; here ν is the spectral dimension of S.

From interpolation theory results, it can be proved (see Section  3.1 in [18]) that
(22)

3.2. The Energy Forms

By Q we denote the parallelepiped as defined in Section 3 and by Sh we denote the prefractal layer of the type Sh = Fh × I, h = 1,2, …, Fh is the prefractal approximation of F at the step h (see Section 2). Sh divides Q in two subsets , i = 1,2.

We first construct the energy forms on the prefractal layers Sh = Fh × I, h ∈ ℕ. By ℓ we denote the natural arc-length coordinate on each edge of Fh and we introduce the coordinates x1 = x1(ℓ), x2 = x2(ℓ), and y = y on every affine “face” of Sh. By dℓ we denote the one-dimensional measure given by the arc-length ℓ and by dσ are denote the surface measure on each face of Sh; that is, dσ = dℓdy. We define by setting
(23)
where and are positive constants and u ∈ H1(Sh), the Sobolev space of functions on the piecewise affine set Sh (see Appendices A and B). By Fubini theorem, we can write this functional in the form
(24)
We denote the corresponding bilinear form by . In the sequel we denote by the symbol the trace γ0f to Sh.
Consider now the space of functions u : Q → ℝ as
(25)
it is not trivial as it contains 𝒟(Q).
Consider now the energy form
(26)
defined on the domain V(Q, Sh).
By E(h)(u, v) we will denote the corresponding bilinear form
(27)
defined on V(Q, Sh) × V(Q, Sh).

Theorem 9. The form E(h), defined in (26), with domain V(Q, Sh) is a regular Dirichlet form in L2(Q) and the space V(Q, Sh) is a Hilbert space equipped with the scalar product

(28)

For the proof, see Theorem  4.1 in [4].

We denote by the corresponding energy norm in V(Q, Sh); that is,
(29)
Proceeding as in Section 3.1 we denote by , Ah, and {Th(t)} t≥0 the resolvents, the generators, and the semigroups associated to E(h), for every h ∈ ℕ, respectively.

As in Proposition 6, the following result can be proved.

Proposition 10. Let {Th(t)} t≥0 be the semigroup generated by the operator Ah associated with the energy form in (27). Then {Th(t)} t≥0 is an analytic contraction positive preserving semigroup in L2(Q).

By proceeding as in Remark 7, one can show that for every h ∈ ℕ the symmetric and contraction analytic semigroup Th(t) uniquely determines analytic semigroups on the space Lp,  1 < p < ∞ (see Theorem 1.4.1 [30]) which we still denote by Th(t) and by its infinitesimal generator.

The following estimate on the decay of the heat semigroup holds (see e.g., [32]).

Proposition 11. There exists a positive constant such that

(30)
where does not depend on h. One considers the cases n = 3 and ν = 2; here ν is the Euclidean dimension of S.

As before by interpolation results it can be proved that
(31)

3.3. The Convergence of Forms and Semigroups

We now recall the results proved in [21] on the convergence of the approximating energy forms E(h) to the fractal energy E. In this asymptotic behaviour, the factors and have a key role and can be regarded as a sort of renormalization factors of the approximating energies. These factors take into account the nonrectifiability of the curve F and hence the irregularity of the surface S and in particular the effect of the D-dimensional length intrinsic to the curve; for details, see [6]. The convergence of functional is here intended in the sense of the M-convergence which we define below.

3.3.1. The M-Convergence of Forms

We recall, for the sake of completeness, the definition of M-convergence of forms introduced by Mosco in [33].

We extend the form E defined in (15) and E(h) defined in (26) on the whole space L2(Q) by defining
(32)

Definition 12. A sequence of form {E(h)} M-converges to a form E in L2(Q) if

  •  

    (a)  for  every {vh} converging weakly to u in L2(Q)

    (33)

  •  

    (b) for  every u ∈ L2(Q) there exists {wh} converging strongly to u in L2(Q) such that

    (34)

Definition 13. The sequence of forms {E(h)} is asymptotically compact in L2(Q) if every sequence {uh} with

(35)
has a subsequence strongly convergent in L2(Q).

Proposition 14. The sequence of forms (26) is asymptotically compact in L2(Q).

Remark 15. We point out that, as the sequence of forms (26) is asymptotically compact in L2(Q), M-convergence is equivalent to the Γ-convergence (see Lemma  2.3.2 in [34]) and thus we can take in (a) vh strongly converging to u in L2(Q).

Theorem 16. Let and ; then the sequence of forms {E(h)} defined in (26) M-converges in the space L2(Q) to the form E defined in (15). The sequence of semigroups {Th(t)} associated with the form E(h) converges to the semigroup T(t) associated with the form E in the strong operator topology of L2(Q) uniformly on every interval [0, t1].

4. Evolution Problems: Existence and Convergence of the Solutions

In this Section we recall the results on existence and uniqueness of the solution of the abstract problems (P) and (Ph) (see below) and the asymptotic behaviour of the solutions of the abstract problems. In Section 5 we will show that the solutions of the abstract problems solve in both cases. We refer the reader to [18].

We consider the abstract Cauchy problems as
(36)
and for every h ∈ ℕ
(37)
where A : 𝒟(A) ⊂ L2(Q) → L2(Q) and Ah : 𝒟(Ah) ⊂ L2(Q) → L2(Q) are the generators associated, respectively, to the energy form E and the energy forms E(h) introduced in (15) and (26), T is a fixed positive real number, and ϕ and ϕh are given functions in L2(Q). We assume that J is a mapping from L2p(Q) → L2(Q), p > 1 locally Lipschitz, that is, Lipschitz on bounded sets in L2p(Q); we let l(r) denote the Lipschitz constant of J:
(38)
where . We also assume that J(0) = 0. This assumption is not necessary in all that follows, but it simplifies the calculations (see [11]). In order to prove the local existence theorem, we make the following assumptions on the growth of l(r) when r → ∞.
We set for brevity a : = (n/4)(1 − (1/p)); we note that 0 < a < 1, for n ≤ 4, and p > 1.
  • (i)

    There exists 0 < b < a such that l(r) = 𝒪(r(1−a)/b),  r → ∞.

  • (ii)

    Consider

    (39)

  •  

    for every τ > 0.

We note that (ii) implies (i) for all 0 < b < a since l(r) is nondecreasing and
(40)
Thus l(r)r1−(1/a) is bounded as r → ∞ which implies (i) for 0 < b < a.

In Theorem 5.1 of [18], the following local existence theorem has been proved.

Theorem 17. Let condition (i) hold. Let K > 0 be sufficiently small if ϕ ∈ L2(Q) and

(41)
There is a T > 0 and a
(42)
with u(0) = ϕ satisfying
  • (1)

    u ∈ C((0, T]; L2p(Q)), and ;

  • (2)

    for every t ∈ [0, T],

    (43)

  •  

    with the integral being both an L2-valued and L2p-valued Bochner integral;

  • (3)

    if v : (0, T1] → L2p is strongly measurable with and also satisfies (43), then u(t) = v(t), for every t ∈ (0, T1].

Let condition (ii) hold; there exist a T > 0 and a unique u(t) ∈ C([0, T]; L2(Q)) with u(0) = ϕ satisfying

  • (1)

    u ∈ C((0, T]; L2p(Q))

    (44)

  • (2)

    for every t ∈ [0, T], u(t) satisfies (43) with the integral being both an L2-valued and L2p-valued Bochner integral;

  • (3)

    if v : (0, T1] → L2p is strongly measurable with bounded and also satisfies (43), then u(t) = v(t), for every t ∈ (0, T1].

The claim of the Theorem is proved by a contraction mapping argument on suitable spaces of continuous functions with values in Banach space.

By exploiting the analyticity of the semigroup T(t) both on L2(Q) and L2p(Q), the following regularity result for the maximal solution holds (see Theorem 5.3 [18]).

Theorem 18. Under the assumptions of Theorem 17, one has that the solution u(t) can be continuously extended to a maximal interval (0, Tϕ) as a solution of (43), until as t → Tϕ, and it is a classical solution; that is,

(45)
and satisfies
(46)

For every fixed h ∈ ℕ, the claims of Theorems 17 and 18 hold for problem (Ph) with the obvious changes.

We now recall the convergence results of the sequence of the approximating solutions {uh} when h goes to infinity (see Theorem  6.2 in [18]).

Theorem 19. Let u and uh be the mild solutions of problems (P) and (Ph); let and be as in Theorem 16. In the notations and assumptions of Theorem 17, one has the following;

  • (a)

    let assumption (i) hold; let ϕh and ϕ belong to Lq(Q) with q = 2pn/(n + 4pb) and ϕh → ϕ in L  q(Q); then

    (47)

  • (b)

    if assumption (ii) holds and ϕh → ϕ in L2(Q), then

    (48)

  •  

    with a = n/4(1 − 1/p).

5. Strong Formulation of the Transmission Problems

5.1. The Fractal Layer

Theorem 20. Let u be the solution of problem (P). Then one has, for every fixed t ∈ (0, T],

(49)
where ui is the restriction of u to Qi, ∂ui/∂ni, i = 1,2 is the inward “normal derivative,” to be defined in a suitable sense, [∂u/∂n] = (∂u1/∂n1) + (∂u2/∂n2) is the jump of the normal derivative, and ΔS is the fractal Laplacian. Moreover .

Proof. Let φ(P) be an arbitrary function in V(Q, S) such that ; by multiplying for φ (36) in (P) and integrating over Q we have

(50)
From (19) and taking into account that φ ∈ 𝒟(Qi), we have
(51)
From the arbitrariness of φ, we have that, for fixed t ∈ (0, T],
(52)
From the density of 𝒟(Qi) in L2(Qi) and since J(u(t, ·)) ∈ L2(Q), we obtain the first assertion in (49). From this equality, we obtain Δu(t, P) = ut(t, P) − J(u(t, P)) and since the right-hand side belongs to C((0, T]; L2(Qi)) we deduce that Δu(t, P) ∈ C((0, T]; L2(Qi)); hence u(t, ·)   ∈ C((0, T]; V(Qi)), where
(53)
here the Laplacian is intended in the distributional sense. By proceeding as in (3.26) of [4], we prove that, for every fixed t, the normal derivative ∂ui/∂ni is in the dual of the space , where β = df/2 and
(54)
for every t ∈ (0, T] and every . By proceeding as in Section 6.1 of [21], we can prove that .

From Proposition 4 and proceeding as in Section 6 of [3], it can be proved that the transmission condition

(55)
That is, for every t ∈ (0, T],
(56)
As a consequence of Theorem 20, the solution of problem (P) is the solution of the following transmission problem. For every t ∈ (0, T],
  •  

    (j)

    (57)

  •  

    (jj)

    (58)

  •  

    (jjj)

    (59)

  •  

    (jv)

    (60)

  •  

    (v)

    (61)

Remark 21. Actually from Proposition 6, one deduces that equalities (jv) and (v), respectively, hold in and in with α < 1.

5.2. The Prefractal Layer

Theorem 22. Let uh be the solution of problem (Ph). Then one has, for every fixed t ∈ (0, T],

(62)
where is the restriction of uh to , is the jump of the normal derivatives across Sh, ni, i = 1,2, is the inward normal vector, and is the piecewise tangential Laplacian associated to the Dirichlet form . Moreover .

Proof. The first equality in (62) easily follows by proceeding as in Theorem 20. From this, it follows that, for every t ∈ [0, T],

(63)
For every fixed t ∈ (0, T], let denote the restriction of the solution uh to . By usual duality arguments (see Appendix  4 in [35]), the normal derivatives , i = 1,2 belong to the dual space of . By proceeding as in Section 6.2 of [21], it is possible to prove that .

Then, by the Green formula for Lipschitz domains, one can prove that

(64)
That is, the transmission condition
(65)
holds in the dual of (see Proposition  2.2 in [5] for details). In order to prove that , we proceed as in Section 4.2 of [4]. Let us consider, for each fixed t ∈ (0, T], the weak solutions and in of the following auxiliary problems:
(66)
(67)
The regularity of follows from the regularity of and since
(68)
From a regularity result of Jerison and Kenig (see Theorems 2 and 3 of [36]), we deduce that
(69)
and .

As to the solution of (67), we preliminary observe that the right-hand side in the first equation of (67) belongs to . From Proposition  4.5 in [4], it follows that

(70)
where 1 < s1 < 8/5 and 1 < s2 < 7/4; hence
(71)
for every ϵ > 0; then by trace results (see Proposition A.1), we obtain, for i = 1,2,
(72)
and . It follows from (67), (68), and (69) that , i = 1,2; hence the jump belongs to L2(Sh). As is dense in L2(Sh) (see e.g., [37]), we deduce that the transmission condition (64) actually holds in the L2-sense and in particular . The proof that easily follows from (69), (72), and the fact that uh, Ahuh, J(uh), and belong to C((0, T]; L2(Q)).

From Theorem 22, it follows that the solution of problem (Ph) is the solution of the following transmission problem. For every t ∈ (0, T],

  •  

    (j)

    (73)

  •  

    (jj)

    (74)

  •  

    (jjj)

    (75)

  •  

    (jv)

    (76)

  •  

    (v)

    (77)

6. Convergence Results

Now we are interested in the behavior of the sequence {uh} when h goes to ∞.

Theorem 23. Let u and uh be the solutions of problems (P) and (Ph) according to Theorem 19. Let and be as in Theorem 16. For every fixed positive ϵ, one has

  • (i)

    J(uh) converges to J(u) in L2([ϵ, T] × Q);

  • (ii)

    {duh/dt} weakly converges to du/dt in L2([ϵ, T] × Q);

  • (iii)

    {Ahuh} weakly converges to Au in L2([ϵ, T] × Q);

  • (iv)

    {uh} converges to u in .

Proof. We prove condition (i), that is,

(78)
From (38), we have
(79)
From Theorem 19 (a), we have
(80)
And hence, for every fixed ϵ > 0,
(81)
This concludes the proof of condition (i).

We now prove condition (ii). From the local Lipschitz continuity of J(u) and the Hölder continuity of uh(t) in (ϵ, T) into L2p, one can prove that is bounded by a constant which does not depend on h; actually the constants depend only on the constants of the semigroups which in turn do not depend on h. From this, together with Theorem 18, we have that there exists a constant c independent of h such that

(82)

Thus in particular it holds ; thus, for every fixed t ∈ [ϵ, T], .

From (82), it follows that for each h, duh/dt belongs to L2([ϵ, T] × Q) and .

From the boundedness of the sequence {duh/dt} in L2([ϵ, T] × Q), it follows that there exists a subsequence, which we denote with {duh/dt} and a function v ∈ L2([ϵ, T] × Q) such that {duh/dt} weakly converges to v in L2([ϵ, T] × Q) as h goes to ∞.

In order to prove (ii), it is enough to prove that v = du/dt.

Since C1([ϵ, T] × Q) is dense in L2([ϵ, T] × Q), for every φ ∈   C1([ϵ, T] × Q), we have

(83)

Integrating by parts the left-hand side, we get

(84)
From (47) or (48), we have
(85)
From the uniqueness of weak limit, we get v = du/dt a.e.. From the convergence of the sequence {uh} to u in L2([ϵ, T]   ×   Q) and the weak convergence of the subsequence {dun/dt} to du/dt in L2([ϵ, T]   ×   Q), we deduce that the whole sequence {duh/dt} weakly converges to du/dt in L2([ϵ, T]   ×   Q).

We now prove condition (iii). It is an easy consequence of (i) and (ii). In fact Ahuh = (duh/dt) − J(uh); taking the weak limit in L2([ϵ, T] × Q), we get the thesis.

We now prove condition (iv). From (i), (iii), and the property of the scalar product in L2([ϵ, T] × Q), we get that

(86)
That is,
(87)
From the relation between a Dirichlet form and the associated generator, it follows that
(88)
There exists a constant c such that
(89)
Hence
(90)
There exists a subsequence Dun weakly converging to w in L2([ϵ, T] × Q) 3. We now prove that
(91)
From Theorem 19, it follows in particular that un converges to u in L2([ϵ, T] × Q); hence w = Du and uh⇀u in ; in particular (91) holds. We now prove assertion (iv) as
(92)
Taking the upper limit as h → ∞, we have
(93)
(94)
(95)
where the last inequality follows from (4.9) in [21]. Hence the sequence {uh} converges to u in and therefore {Duh} converges to Du in L2([ϵ, T];   (L2(Q)) 3).

Proposition 24. Let u and uh be the solutions of problems (P) and (Ph), respectively. Then u and uh ∈ H1([ϵ, T] × Q).

Proof. We prove the thesis for u. From Theorem 18, it follows that u ∈ C([ϵ, T]; 𝒟(A)) and (du/dt) ∈ C([ϵ, T]; L2(Q)). Since , we obtain ; hence Du ∈ C([ϵ, T]; (L2(Q)) 3). The thesis follows as C([ϵ, T]; L2(Q)) ⊂ L2([ϵ, T] × Q). The result for uh can be proved analogously.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

This research was partially supported under the Grant no. 1109356 by Fractal Fibers and Singular Homogeneization National Science Foundation.

    Appendices

    Here we recall some definitions of functional spaces and trace results.

    A. Sobolev Spaces

    Let Q be a polyhedral domain; just to fix the ideas, the parallelepiped is as in Section 2. For every integer h ≥ 1, let Sh be the prefractal surface approximating the Koch-type surface S and let us denote every affine “face” of Sh by ; Sh divides Q into two subsets and .

    By Lp(·), p > 1 we denote the Lebesgue space with respect to the Lebesgue measure on subsets of ℝ3, which will be left to the context whenever that does not create ambiguity. Let 𝒯 be a closed set of ℝ3; by C(𝒯) we denote the space of continuous functions on 𝒯; by C0(𝒯) we denote the space of continuous functions vanishing on ∂𝒯. Let 𝒢 be an open set of ℝ3; by H1(𝒢) we denote the usual Sobolev spaces (see Necas [38]); is the closure of 𝒟(𝒢) (the smooth functions with compact support on 𝒢), with respect to the -norm. In the following, we will make use of trace spaces on boundaries of polyhedral domains of ℝ3.

    By we denote the closure in H1(Sh) of the set
    (A.1)
    By Hr(Sh), 0 < r ≤ 1 we denote the Sobolev space on Sh, defined by local Lipschitz charts as in Necas [38].

    It is to be pointed out that the Sobolev space Hr(Sh) (defined in [38]) coincides, with equivalent norms, with the trace space defined in Buffa and Ciarlet in [37] (see also [39] for the case of polygonal boundaries).

    When r > 1, the trace spaces on nonsmooth boundaries can be defined in different ways; we now recall two trace theorems, specialized to our case, referring to [40] and [41] for a more general discussion.

    For f in H1(𝒢), we put
    (A.2)
    at every point , where the limit exists. It is known that the limit (A.2) exists at quasi every with respect to the (1,2)-capacity [42].

    We now recall the results of Theorem  3.1 in [36] specialized to our case, referring to [41] for a more general discussion.

    Proposition A.1. Let 𝒢 denote, respectively, , and  and let Γ denote Sh, , , and ∂Q. Then H1/2(Γ) is the trace space to Γ of H1(𝒢) in the following sense:

    • (i)

      γ0 is a continuous and linear operator from H1(𝒢) to H1/2(Γ);

    • (ii)

      there is a continuous linear operator Ext⁡ from H1/2(Γ) to H1(𝒢), such that γ0∘Ext⁡ is the identity operator in H1/2(Γ).

    B. Besov Spaces

    Definition B.1. Let 𝒯 ⊂ ℝD be a closed nonempty subset. It is a d-set  (0 < d ≤ D) if there exists a Borel measure μ with supp⁡  μ = 𝒯 such that, for some constants c1 = c1(𝒯) > 0 and c2 = c2(𝒯) > 0,

    (B.1)
    Such a μ is called a d-measure on 𝒯.

    Proposition B.2. The set F is a d-set with d = df. The measure μF is a d-measure. The layer S is a d-set with d = df + 1. The measure m is a d-measure.

    See [23, 26].

    We now come to the definition of the Besov spaces. Actually there are many equivalent definitions of these spaces; see, for instance, [43, 44]. We recall here the one which best fits our aims and we will restrict ourselves to the case α positive and noninteger, p = q = 2; the general setting is being much more involved; see [44].

    Let 𝒯 be a d-set in ℝD.

    Let α > 0 be noninteger, k = [α] the integer part of α, and j a D-dimensional multi-index of length |j| ≤ k.

    If f and {f(j)} are functions defined μ-a.e. on 𝒯, we set
    (B.2)
    where f(0) = f and l denotes a D-dimensional multi-index. We now define the Besov space as .

    Definition B.3. One says that if there exists a family {f(j)} with |j| ≤ k, as above, such that f(j) ∈ L2(𝒯, μ) and , where an is the smallest number such that

    (B.3)
    The norm of f in is
    (B.4)
    The family {f(j)} in the previous definition is uniquely determined by f, as shown in [44], for d-sets with d > D − 1.

    Let us note that for 0 < α < 1 the norm can be written as
    (B.5)

    Proposition B.4. Let 𝒯 be a d-set, . Let s > (3 − d)/2, (s − (3 − d)/2) ∉ ℕ); then is the trace space to 𝒯 of Hs(Q) in the following sense:

    • (i)

      γ0  is a continuous linear operator from  Hs(Q)  to  ;

    • (ii)

      there is a continuous linear operator  Ext  from    to  Hs(Q)  such  that  γ0∘Ext⁡  is the identity operator in .

    For the proof, we refer to Theorem 1 of Chapter VII in [44]; see also [43].

    From Proposition B.4, it follows that when 𝒯 = S and s = 1 the trace space of H1(Q) is .

    Let β = df/2. The space is a subspace of ; more precisely
    (B.6)
    equipped with the norm
    (B.7)

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.