The passenger travel demands for intercity rail lines fluctuate obviously during different time periods, which makes the rail departments unable to establish an even train operation scheme. This paper considers an optimization problem for train operations which respond to passenger travel demands of different periods in intercity rail lines. A satisfactory function of passenger travelling is proposed by means of analyzing the passengers’ travel choice behavior and correlative influencing factors. On this basis, the paper formulates a bilevel programming model which maximizes interests of railway enterprises and travelling satisfaction of each passenger. The trains operation in different periods can be optimized through upper layer planning of the model, while considering the passenger flow distribution problem based on the Wardrop user equilibrium principle in the lower layer planning. Then, a genetic algorithm is designed according to model features for solving the upper laying. The Frank-Wolfe algorithm is used for solving the lower layer planning. Finally, a numerical example is provided to demonstrate the application of the method proposed in this paper.

1. Introduction

On intercity rail lines, the train dispatching density is quite high and passengers normally choose their travel time according to their own travel habits. The passenger travel demand varies at different time periods, and the distribution of passenger flow during the day has obvious peaks and troughs. The railway department will fully consider the characteristic of passengers’ travel time when setting the train operation scheme of intercity rail lines. If the evened train dispatching mode is adopted for the whole day, it will cause the dissatisfaction of the demands in some peak periods and excess supply in some trough periods. Therefore, to divide the service time into several periods and adopt the evenly dispatching mode based on period will make a better balance between passengers’ travel demand and benefits of railway transportation. In addition, passengers will also consider traveling in high-satisfactory time periods according to the train operation scheme. Therefore, to develop a reasonable operation scheme can effectively eliminate the shortage issue of dispatching capacity on stations during peak hours, also leading passengers to travel at different time periods without reducing their travel satisfactions.

Domestic and overseas scholars have done a great amount of researches on the passenger train operation scheme of railway transportation. Considering that the traveling characteristic of intercity passenger flow is different from that of ordinary railway, some scholars have analyzed and researched passenger flow characteristics of intercity railway. Through massive investigation data, Mandel et al. have done a systematic research on the high-speed railway market and analyzed the fact that the characteristics of passengers’ demand are similar to those of city bus passenger demands on high-speed railway in Germany [1]. Zhao has systematically analyzed the fact that the traveling characteristics of intercity railway passenger flow are remarkably different from those of the urban residents in the aspects of traveling objective, time, intensity, distance, cost, and distribution [2]. Through numerous researches by domestic and overseas scholars, it is found that the passenger flow of intercity railway has a higher variability, on the elastic demand of which some scholars have done researches. Cascetta and Coppola have established an optimized model of train operation timetable under the elastic demand, aiming to optimize the ticket pricing structure of high-speed railway [3]. Shi et al. have analyzed the affecting factors related to the passenger train operation scheme and constructed a function of elastic passengers’ transport demand [4]. Some scholars believe that the reasonable distribution of passenger flow is the premise of optimizing the passenger train operation scheme. Peng and Zhu have described the interactive relationship between transport demand and the operation scheme, established a dynamic assignment model of passenger flow which reflects the transition process for different types of passenger flow, and constructed multiobjective planning model which gives a comprehensive consideration to maximum benefit of railway department, minimum total cost of passenger, and satisfaction of passenger flow demand to the greatest extent [5]. Some scholars have given enough thought to the impact of congestion on passengers’ travel when optimizing the train operation scheme. Niu and Zhou have studied the optimizing issue of train timetable for city rail transportation under time-varying and congestion condition. Using time-varying based passenger flow data collected from the automatic ticket inspection system of city rail transportation, they established the nonlinear integer planning model for dispatching trains on rail under the given condition by the number of motor train units [6]. There are many issues to be taken into account in order to develop a reasonable passenger train operation scheme, and the various factors often have association relationship with each other. Therefore, some scholars have tried to establish bilevel planning model to give mathematical description to this issue and obtained certain achievements. He et al. have analyzed the balancing condition of passenger flow for different types of trains and established the generalized cost function for different types of trains, based on which they have constructed multiobjective bilevel planning model for developing the dedicated passenger train operation scheme. This model takes the maximum benefit of train operation and maximum convenient degree of passenger as target and also considers the assignment issue of different types of trains based on minimum travel cost to passengers [7]. Shi et al. have analyzed the relevant cost and optimizing objective of the passenger train operation scheme, evenly considered the enterprise profit and the passengers’ demand, combined the train operation scheme and passenger transference scheme, and established the optimized bilevel planning model of the passenger train operation scheme which takes distribution of passenger flow in railway transference network as the lower layer planning [8]. Considering that the intercity railway train operation scheme may affect the travel convenience of passenger flow and passenger’s satisfactory degree, He et al. have studied the convenience for passengers in different time periods based on market investigation data [7]. Chang et al. developed a multiobjective programming model for the optimal allocation of passenger train service on an intercity high-speed rail line without branches. Minimizing the operator’s total operating cost and minimizing the passenger’s total travel time loss are the two planning objectives of the model [9]. Huang and Niu have analyzed the relevant factors that affected the traveling satisfaction of passengers and established an optimized model of train operation scheme aiming at getting maximum traveling satisfaction of passengers [10]. However, the above research did not consider the effect of passenger flow distribution for passengers’ satisfaction and the feedback relationship between train operations scheme and passengers’ demand. Therefore, this paper will construct a bilevel programming model to optimize train operations based on passengers’ satisfaction.

The remainder of this paper is organized as follows: Section 2 presents and analyzes the researching issues; Section 3 establishes bilevel planning model of intercity railway train operation scheme; Section 4 gets solution by adopting genetic algorithm based on model features; Section 5 verifies the model through examples; in the end, the content of study in this paper and the further issues to be researched are summarized.

2. Problem Statement

2.1. Division of Passenger Travelling Time Period

On intercity rail lines, different passengers will choose different travelling time periods based on their own demands. For example, some passengers will make decisions on travelling time in accordance with their habits; some will do so according to the congestion level of urban traffic, while some will do it as requested by their working hours and so on. However, through the research on the travelling time period of intercity railway passengers, it shows that passenger flow is not distributed equally in different time periods but has obvious peaks and troughs throughout the day.

According to the above analysis, the passengers’ travel demand is uneven in different time periods. Therefore, the passenger travel demand in different time periods needs to be taken into account when developing the intercity railway train operation scheme. In order to make an easy study, this paper divides the service time of intercity rail lines into m travel periods by hour; that is, one hour represents one travel period. P serves as the set of travelling time periods and P ∈ {p∣1,2, …, m}.

2.2. Generalized Passenger Travel Cost

Passengers must pay the cost of ticket and time when travelling. Thereof, time cost consists of two parts: waiting time cost and travelling time cost. Waiting time cost means the average waiting time after the passenger arrives at the station; travelling time cost is the time period that passenger has to spend in order to complete the spatial displacement, which remains unchanged when the train speed is constant. Therefore, only the waiting time cost will be taken into consideration in this paper. Meanwhile, as congestion causes inconvenience for passenger’s travelling, congestion cost is used to quantize the passenger’s travelling convenient degree in this paper. The generalized passenger travel cost defined in this paper includes three parts: ticket cost, waiting time cost, and congestion cost, as shown in

(1)

Thereof, V_p is the generalized travel cost of each passenger in the time period p; C is the ticket cost; λ is the time value of passenger; t_p is the average waiting time of each passenger in the travelling time period p (the variation of the value is related to the train dispatching intervals, as shown in formula (2)); k_p is the congestion cost for the passengers in the travelling time period p (the value is on the basis of ticket cost, as shown in formula (3)). We have

(2)

where I_p is the train dispatching intervals in the travelling time period p, and

(3)

where Q_p is the passenger flow volume which is assigned in the travelling time period p; N is the service capacity of the station; exp⁡(i) is the natural exponential function. The greater the N/Q_p, the lower the passenger congestion (the value exp⁡(−N/Q_p) at this point gets closer to zero); the smaller the N/Q_p, the higher the level of passenger congestion (the value exp⁡(−N/Q_p) at this point gets closer to 1).

2.3. Passenger’s Travelling Satisfaction

The passenger’s travelling satisfaction defined in this paper means the satisfaction level of expected travelling time and the generalized travel cost for all passengers in the same time period. The factors affecting passenger’s travelling satisfaction include two parts as follows.

(1) Average Satisfaction Level of Travelling Time Period. As previously mentioned, different passengers will choose different travelling time periods according to their own demands. The key factor affecting the passenger’s satisfaction is whether enough transportation capacity could be provided by the railway department according to the passenger’s demand of travelling time period. The average passenger satisfaction A_p of the travelling time period p is

(4)

where M_p is the passenger demand of the travelling time period p, which can be obtained through market survey; when Q_p ≥ M_p, it indicates all passengers expecting to travel at the p time period, whose demands on travelling time can be satisfied. When Q_p < M_p, it indicates that some passengers have to choose other time periods, and therefore the average satisfaction of the passengers will decrease. The value range of Q_p/M_p is [0,1). The smaller the Q_p is, the lower the passenger’s average satisfaction gets.

(2) Passenger Satisfaction of Generalized Travel Cost. Passengers always expect the minimum travel cost. The lower the generalized cost of passenger’s travelling is, the higher its satisfaction gets. The passenger’s travelling satisfaction B_p of generalized cost in the travelling time period p is

(5)

As mentioned above, the ticket cost C that passenger has to pay when travelling is a set value, while the generalized cost V_p paid by passenger at the travelling time period p is a variable value. V_p − C shows the extra cost paid by passenger in addition to the ticket cost. The more this part costs, the lower the passenger’s satisfaction level gets.

Through the above analysis, the passenger’s travelling satisfaction presents a dynamic balance. When passenger can travel according to his/her expected time period, he/she may pay a higher generalized cost and his/her travelling satisfaction will decrease. Therefore, to better describe this dynamic balance status, a satisfactory function of passenger travelling at the p time period is constructed in this paper, as follows:

(6)

where ρ indicates the passenger’s preference of the travelling time period satisfaction and 0 < ρ < 1.

3. Bilevel Planning Model

3.1. Lower Layer Planning

(1) Equilibrium Assignment Conditions of Passenger Flow. As mentioned above, passengers always expect the maximum satisfaction when travelling. Under the condition that the train operation scheme is set, passengers will choose their travel plans with the maximum satisfaction. It is incompatible with passenger flow equilibrium assignment condition of minimum travelling impedance in UE assignment model. Therefore, according to the feature of value range [0,1] in satisfaction function g_p(Q_P), the paper constructs an Impendence Function suitable for lower layer planning in this paper, as shown in

(7)

The value range of y_p(Q_p) is [0,1] and minimum of y_p(Q_p) equals maximum of g_p(Q_P). According to utility theory, among all the optional travel plans, the impedances of all the plans chosen by passengers are the same and not greater than those of the unselected plans, as shown in

(8)

where y_p is the travel impedance of each passenger in the travelling time period p; y_min⁡ is the travel impedance under balanced status.

(2) Equilibrium Assignment Model. The paper has done an equivalent exchange to the UE assignment model proposed by Beckmann. The following formula is the objective function:

(9)

where the upper limit h_p of integral indicates the segment flow on the route p.

Formula (10) is the sum of passenger flow on all routes. This constraint indicates conservation relation between the route flow and total passenger flow demand:

(10)

The following formula ensures that all the route flows are positive, thus satisfying the equilibrium assignment condition of passenger flow expressed in formula (9):

(11)

The following formula is the relationship of segment flow and route flow:

(12)

This paper constructs passenger travel network, and every travelling time period is one route, with total of m routes. One route only has one segment. Therefore, segment flow h_p is the route flow Q_p.

3.2. Upper Layer Planning

(1) Objective Function. The objective of upper layer planning is to maximize the economic benefits of the railway transportation enterprises, as follows:

(13)

where X_p is the quantity of trains operated in the travelling time period p; W is the operation cost of a single train; C · Q_p is the ticket revenue; W · X_p is the operation cost for all trains in the travelling time period p.

(2) Dispatching Capacity Constraints of the Station. On the intercity railway, section carrying capacity is relatively sufficient comparing with the transport demand. However, the dispatching capacities of peak-hour time periods may not meet the transport demand of that time period. Therefore, dispatching capacity constraints should be considered when developing the upper layer planning model, as shown in

(14)

where n_p is the dispatching capacity of the travelling time period p.

(3) Constraint of Passenger Flow Demand. As mentioned above, passenger flow has obvious variability, and the passenger flow demand may be greater than the dispatching capacity during some time periods of the day. But the transport capacity provided by all the trains operating throughout the day will be greater than the sum of passenger flow demands at each time period of the day, as shown in

(15)

where D is the maximum seats of a train and ∑_p∈PD · X_p shows the seating capacity of all trains provided by the railway department during one day.

(4) Passenger Flow Constraints of Each Time Period. Consider

(16)

D · X_p shows that the seating capacity provided by the railway department in the travelling time period p should be able to satisfy the passenger flow Q_p of that time period.

(5) Train Overload Constraint. During passenger flow peak hours, standing ticket is allowed to sell on the intercity railway. For example, the standing tickets have reached 20% during peak hours on Beijing-Tianjin Intercity Railway. Therefore, this paper proposes train overload constraint, as shown in

(17)

where mod⁡ is the calculation of dividing modulus and keeping remainder and π is the maximum overload coefficient of the train.

(6) Nonnegativity and Integer Constraint. Consider

(18)

3.3. Associations Relationship between Upper Layer Planning and Lower Layer Planning

Lower layer planning satisfies the UE flow distribution under the Wardrop equilibrium assignment condition and could generate the passenger flow distribution scheme Q_p according to the passenger flow equilibrium assignment condition. Upper layer planning is the optimized model aiming at maximizing the railway operational benefit and can obtain the train operation scheme X_p through optimizing calculation.

Upper layer planning and lower layer planning are not isolated but correlated with each other. Based on the train operation scheme X_p defined by upper layer planning, the correlation parameters of Impendence Function for lower layer planning can be obtained as

(19)

This paper assumes that trains are evenly dispatched at one time period and each travelling time period equals 1 hour without exception. Therefore, 1/X_p shows the train dispatching interval of the time period p.

According to the passenger flow distribution scheme Q_p of lower layer planning, the ticket revenue ∑_p∈PC · Q_p of upper layer planning and passenger flow constraint conditions of each time period can be obtained.

Through the nested calculation of the upper layer and lower layer planning, this paper proposes the equilibrium relationship between upper layer optimized scheme X_p and passenger flow distribution scheme Q_p of lower layer, as follows:

(20)

(21)

where ceil(j) is rounddown function and η is the minimum occupancy rate of the train; θ is variable between 0 and 1, the value of which is calculated according to formula (21).

4. Algorithm Design

The model established in this paper is a bilevel planning problem of nonlinear mixed integer and is widely acknowledged as one of the optimization problems that are extremely difficult to solve. This paper adopts a genetic algorithm to get the solution of the model. This algorithm has better global convergence and is able to search for satisfactory solution in a short time, the core concept of which is to keep the high fitness of the individual to the next generation while eliminating the low fitness ones, based on the principle of natural evolution “Survival of the fittest."

4.1. Genetic Algorithm Design

(1) Chromosome Coding. Chromosome is made up of m gene segments which indicate m travelling time periods, respectively. Integer coding is used for chromosome coding. The position of each chromosome indicates the quantity of dispatched trains in the corresponding time period. The structure is as shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Chromosome structure.

(2) Fitness Function. In the genetic algorithm, whether the individual can be kept to the next generation is determined by its fitness. The higher the individual fitness is, the bigger possibility it gets to be transmitted to the next generation; conversely the possibility is smaller. This paper adopts the following formula as a fitness function:

(22)

In the formula, E indicates the target value of chromosome.

(3) Genetic Operation. Genetic operation (selection operation, crossover operation, and mutation operation) is the core step of genetic algorithm, and it can produce a new generation through the genetic operation to the population. This paper adopts the improved crossover mutation method in literature [11].

4.2. Algorithm Process

Step 1 (initialization). According to the above described chromosome coding regulations and formulae (14)–(18), randomly generate the initial population of feasible solution with the scale of popsize; set optimal goal E^* = 0 of the upper layer planning; initialize operation scheme WP^* to zero vector; proposal inspection set Ψ is an empty set; the number of iterations is t = 1.

Step 2 (genetic operation). Based on the genetic algorithm designed in Section 4.1, conduct the selection, crossover, and mutation operation to the initial population, and search for feasible solution (operation scheme) WP^t with the highest fitness in the current population; the number of iterations is t = t + 1.

Step 3 (checking). If WP^t ∉ Ψ, then add it into check set Ψ and go to Step 4; otherwise, go to Step 2.

Step 4 (user equilibrium assignment). For the current operation scheme WP^t, use the Frank-Wolfe algorithm to get solution for lower layer planning, and obtain Q_pt in conformity with the Wardrop user equilibrium criterion.

Step 5. Bring the current operation scheme WP^t and passenger flow demand Q_pt into the upper layer objective function, and calculate the objective function E; if E > E^*, then let E^* = E and WP^* = WP^t.

Step 6 (termination of inspection). If the number of iterations t is greater than the upper limits G, then generate the optimal solution WP^*; otherwise, go to Step 2.

5. Numerical Example

The paper takes the optimization of train operation scheme on Beijing-Tianjin Intercity Railway as an example to verify the model and algorithm presented in this paper.

5.1. Parameter Value

(1) Division of Time Period. The paper divides the service time (7:00–23:00) of Beijing-Tianjin Intercity Railway into 17 intervals, on the basis of one hour per interval.

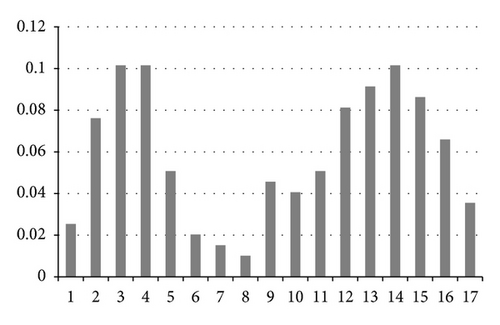
(2) Passenger Travel Demands. The paper uses the official forecast data of the Beijing Railway Bureau. The average daily passengers would reach 117,400 by 2015 on Beijing-Tianjin Intercity Railway; that is, M = 117400. According to passenger flow survey, the passenger travel demand proportion of different time periods on Beijing-Tianjin Intercity Railway is as shown in Figure 2. Therefore, the passenger travel demand M_p in each time period is as shown in Table 1.

Table 1. Passenger travel demands of different time periods on Beijing-Tianjin Intercity Railway.

p	1	2	3	4	5	6	7	8	9
M_p	2980	8939	11919	11919	5959	2384	1788	1192	5363
p	10	11	12	13	14	15	16	17
M_p	4768	5959	9535	10727	11919	10131	7747	4172

(3) Relevant Operation Parameters of Beijing-Tianjin Intercity Railway. Relevant operation parameters are set as [8, 9]: C is 57.25 yuan, D is 928 person, W is 18000 yuan/train, N is 5000 person, λ is 21.3 yuan, π is 0.2, η is 0.6, n_p = {10,12,12,10,10, 10,10,10,10,10, 12,12,12,10, 10,10,10 }, and p ∈ P.

(4) Algorithm Parameter Settings. According to the algorithm designed in the paper, the population size popsize = 100; obtaining crossover probability P_c = 0.6 and mutation probability P_m = 0.4 based on experience, the maximum stagnation iteration number is 15 and the maximum iteration number is 500.

5.2. Calculation Result and Analysis

This paper considers three kinds of situations, ρ = 0.25, ρ = 0.5, and ρ = 0.75, and calculates the passenger flow Q_p, quantity of trains operated X_p, and average occupancy rate τ_p in each time period, respectively. The calculation result is as shown in Table 2.

Table 2. Calculation result.

p	ρ = 0.25			ρ = 0.5			ρ = 0.75
p	Q_p	X_p	τ_p	Q_p	X_p	τ_p	Q_p	X_p	τ_p
1	6212	7	0.96	6763	7	1.04	6084	7	0.94
2	6212	7	0.96	8846	10	0.95	8196	9	0.98
3	5218	6	0.94	6763	7	1.04	10014	11	0.98
4	8324	9	1	7310	8	0.98	8068	9	0.97
5	7454	8	1	7586	8	1.02	7301	8	0.98
6	7827	8	1.05	6043	7	0.93	5635	6	1.01
7	6833	7	1.05	6783	7	1.04	3458	4	0.93
8	5466	6	0.98	6783	7	1.04	7556	8	1.02
9	7206	8	0.97	5566	6	1	7684	8	1.04
10	7206	8	0.97	8390	9	1	7300	8	0.98
11	8199	9	0.98	8866	10	0.96	6403	7	0.99
12	5218	6	0.94	3923	4	1.06	6019	6	1.08
13	9939	11	0.97	7023	8	0.95	8196	9	0.98
14	6460	7	0.99	6773	7	1.04	8837	10	0.95
15	4100	4	1.1	6773	7	1.04	6916	7	1.06
16	9314	10	1	6470	7	1	4354	5	0.94
17	6212	7	0.96	6739	7	1.04	5379	6	0.97

Total	117400	128	/	117400	126	/	117400	128	/

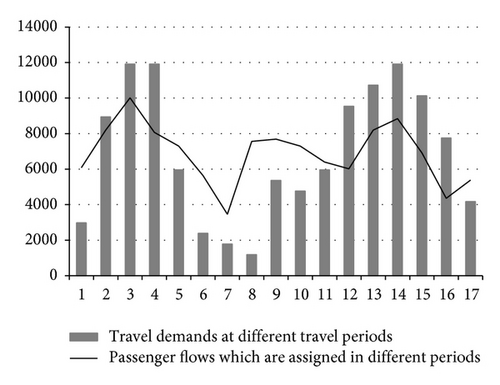
The paper obtains the following information based on the calculation data in Table 2. (1) Quantity of trains operated X_p in each time period is less than dispatching capacity n_p, which meets the train operation condition. (2) Average train occupancy rate τ_p of each time period is greater than the minimum occupancy rate η and τ_p − 1 is less than the maximum overload rate π. (3) When ρ increases, passenger’s requirements of travelling time period satisfaction rise and passenger flow Q_p shows obvious peaks and troughs in each time period. When ρ = 0.75, passenger flow Q_p changing trend of each time period is consistent with transport demand M_p to the greatest extent, as shown in Figure 3. (4) When ρ = 0.5, the total number of dispatched trains in all time periods is 126; when ρ = 0.75 and ρ = 0.25, the total number of dispatched trains in all time periods is 128.

6. Conclusions

The paper applies the UE equilibrium assignment theory to the decision of travel plans for intercity railway passengers and proposes the bilevel planning model of train operation scheme on intercity rail lines. Aiming at maximizing passenger’s average travelling satisfaction, the paper constructs the passenger’s travel impedance function and uses this function as passenger flow equilibrium assignment condition for lower layer planning to conduct assignment; meanwhile, it takes the maximum benefit of railway transport enterprises as target to make optimization. Through optimizing calculation, it obtains the passenger flow of each time period and the train operation scheme. By analyzing the calculation results, the model and algorithm proposed in this paper can effectively optimize the train operation scheme of intercity rail lines. Next, the paper will conduct a deep research on passenger travel choice under the condition of time-based pricing.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

The work described in the paper was supported by the National Natural Science Foundation of China under Grant no. 71261014.

References

1 Mandel B., Gaudry M., and Rothengatter W., A disaggregate box-cox logit mode choice model of intercity passenger travel in Germany and its implications for high-speed rail demand forecasts, Annals of Regional Science. (1997) 31, no. 2, 99–120, 2-s2.0-0031428838.
10.1007/s001680050041
Web of Science® Google Scholar
2 Zhao C. J., Study on Theory and Application of Inter-City Rail Network Planning, 2009, China Academy of Railway Science, Beijing, China.
Google Scholar
3 Cascetta E. and Coppola P., An elastic demand schedule-based multimodal assignment model for the simulation of high speed rail (HSR) systems, EURO Journal on Transportation and Logistics. (2012) 1, no. 1-2, 3–27.
10.1007/s13676-012-0002-0
Google Scholar
4 Shi F., Huang Z. C., Zhou W. L., and Deng L. B., Optimization on departure time distribution of passenger trains based on user equilibrium analysis, Journal of Railways Science and Engineering. (2008) 5, no. 6, 69–75.
Google Scholar
5 Peng H. Q. and Zhu Y. J., Intercity train operation schemes based on passenger flow dynamic assignment, Journal of Transportation Systems Engineering and Information Technology. (2013) 13, no. 1, 111–117.
10.1016/S1570-6672(13)60094-X
Google Scholar
6 Niu H. M. and Zhou X. S., Optimizing urban rail timetable under time-dependent demand and oversaturated conditions, Transportation Research C. (2013) 36, 212–230.
10.1016/j.trc.2013.08.016
Web of Science® Google Scholar
7 He Y.-Q., Zhang H.-Z., Mao B.-H., and Chen T.-S., Multiobjective bi-level programming model of making train working plan for passenger-only line, Journal of the China Railway Society. (2006) 28, no. 5, 6–10, 2-s2.0-33846183842.
Google Scholar
8 Shi F., Deng L., and Huo L., Bi-level programming model and algorithm of passenger train operation plan, China Railway Science. (2007) 28, no. 3, 110–116, 2-s2.0-34347254219.
Google Scholar
9 Chang Y.-H., Yeh C.-H., and Shen C.-C., A multiobjective model for passenger train services planning: application to Taiwan′s high-speed rail line, Transportation Research B. (2000) 34, no. 2, 91–106, 2-s2.0-0034011719, https://doi.org/10.1016/S0191-2615(99)00013-2.
10.1016/S0191-2615(99)00013-2
Web of Science® Google Scholar
10 Huang Z. and Niu H., Study on the train operation optimization of passenger dedicated lines based on satisfaction, Discrete Dynamics in Nature and Society. (2012) 2012, 11, 451201, https://doi.org/10.1155/2012/451201, MR2984243, ZBL1253.90066.
10.1155/2012/451201
Web of Science® Google Scholar
11 Luo G., Liu E. L., and Wang J., Resource planning optimization in network schedule using genetic algorithms, Joural of Tianjin University. (2004) 32, no. 2, 179–183.
Google Scholar

Citing Literature

All articles

A Bilevel Programming Model to Optimize Train Operation Based on Satisfaction for an Intercity Rail Line

Abstract

1. Introduction

2. Problem Statement