The problem of finite-time stabilization for switched discrete-time systems under both fast and slow switching is addressed. In the fast switching case, the designed static state feedback controller combines controllers for each subsystem and resetting controller at switching instant, it is shown that the resetting controller can reduce the conservativeness on controller design. Then the results are extended to output feedback controller design. Under slow switching, both static state feedback and output feedback controller are designed with admissible average dwell time, respectively. Several numerical examples are given to illustrate the proposed results within this paper.

1. Introduction

A switched system consists of a finite number of subsystems that are switched according to the time variation of the system’s mode of operation. Many physical processes possess switched and hybrid nature [1–3], and switched systems arise in many engineering applications, for example, in motor engine control [4], constrained robotics [5], and networked control systems [6]. Due to their ubiquity in modern engineering problems, switched systems are receiving increasing interest and attention as the recent books [1, 2] and survey articles [3, 7, 8] indicate. Stability and stabilization are the main concerns in the field of switched systems. Many Lyapunov function techniques are effective tools dealing with switched systems [9–11]. Dwell time and average dwell time approaches were employed to study the stability and stabilization of time-dependent switched systems [12–14].

On the other hand, the finite-time stability is a concept dealing with the boundness of system during a fixed finite-time interval, which mainly focuses on admitting the state does not exceed a certain bound during a fixed finite-time interval, for instance, to avoid saturations or the excitation of nonlinear dynamics. A distinction should be made between classical Lyapunov stability and finite-time stability (or short-time stability). The concept of Lyapunov asymptotic stability is largely known to the control community; conversely a system is said to be finite-time stable if, once we fix a time interval, its state does not exceed some bounds during this time interval. Often asymptotic stability is enough for practical applications, but there are some cases where large values of the state are not acceptable, for instance, in the presence of saturations. In these cases, we need to check that these unacceptable values are not attained by the state; for these purposes finite-time stability could be used. Some early results about finite-time stability can be found in [15–17]. More recently, [18] investigated the output feedback finite-time stabilization for continuous linear system. Finite-time stability and stabilization for discrete linear system were investigated in [19]. Moreover, the robust finite-time control for linear switched discrete-time system with norm-bounded disturbance was considered in [20], and continuous-time case is considered in [21].

Similar as indicated for asymptotic stability, the finite-time stability is supposed to be affected significantly by switching among several subsystems [20, 21]. Thus, besides Lyapunov asymptotic stability, another important system property we are interested in is the boundness of the state during the short time interval in which the switching occurs, and it is explicit that the boundness of state during the short time interval could be influenced significantly by the switching. To avoid the state reaching the unacceptable large values caused by switching during the short time interval, the boundness property of state, that is, the finite-time stability, needs to be considered when we design the controller and switching law. However, most of the existing stability results were about Lyapunov stability; few results have been reported in literature about the finite-time stability of switched systems so far. This motivates the present study.

In this paper, solutions for finding state and output feedback controller guaranteeing the finite-time stabilization of switched discrete-time system are given in both fast switching and slow switching case. In fast switching case, a natural idea is to find a single common positive matrix satisfying finite-time stabilization condition for each subsystem to ensure the finite-time stability of closed-loop switched system which is similar to the common Lyapunov function approach dealing with asymptotic stability. However, it often yields overly conservativeness. To reduce the conservativeness our approach is based on searching for a set of positive matrices; furthermore it is worth noting that the controller combines the controller for each subsystem and resetting controller at switching instant which generates a proper state impulsive jumping which could further reduce the conservativeness in finite-time controller design. In slow switching case, the controller design is proposed including the controllers for subsystems and the admissible average dwell time. The results in fast and slow switching case are both extended to output feedback case. Several numerical simulations are proposed to show the effectiveness of our approach.

The rest of this paper is organized as follows. In Section 2 the problem formulation and some preliminaries are introduced. The main results, finite-time stabilization under fast switching and slow switching, are given in Sections 3 and 4, respectively; several numerical simulations are given to illustrate our proposed results. Conclusions are given in Section 5.

Notations. The notations used in this paper are fairly standard. The superscript “T” stands for matrix transposition, denotes the n-dimensional Euclidean space and represents the set of nonnegative integers, and the notation ‖·‖ refers to the Euclidean norm. In addition, in symmetric block matrices, we use * as an ellipsis for the terms that are introduced by symmetry and diag⁡{⋯} stands for a block-diagonal matrix. λ_min⁡(P) and λ_max⁡(P) stand for the smallest and the largest eigenvalue of matrix P. The notation P > 0 (P ≥ 0) means P is real symmetric and positive definite (semipositive definite).

2. Preliminaries

In this paper, a switched discrete-time system we consider is described as follows:

()

where

is the discrete state,

is the control input, and

is the measurement of the system. A_i, B_i, and C_i are real known constant matrices with appropriate dimensions.

is a piecewisely constant function of discrete-time k, called switching law or switching signal, which takes its values in finite set

. N > 0 is the number of subsystems. For simplicity, at any arbitrary discrete-time

the switching signal i(k) is denoted by i. Given switched system ((1a), (1b)), the switching sequence can be defined as

, where k₀ denotes the initial time and k_l denotes the lth switching instant. In this paper, we assume that the switching signal is available in real time; that is, the activated subsystem is explicitly known at each switching instant and the corresponding controller can be activated immediately.

For switched discrete-time system, the general conception of finite-time stability concerns the boundness of discrete state x(k) over finite discrete-time interval [0, M], with respect to given initial condition x₀. This conception can be formulized through following definition.

Definition 1 (finite-time stability). Switched system

()

is said to be finite-time stable with respect to (δ, ε, R, M), where 0 ≤ δ < ε, R is a positive definite matrix, and

, if x^T(k)Rx(k) < ε², ∀k ∈ {1,2, …, M} whenever

Then we recall the following lemma, which will be used in the proof of our main results.

Lemma 2 (see [22].)The linear matrix inequality

()

where

and

are equivalent to

()

Lemma 2 is the well-known Schur complement lemma.

3. Finite-Time Stabilization under Fast Switching

In this section we consider the finite-time stabilization for switched discrete-time system under fast switching. A set of static state feedback controllers are given as u(k) = K_ix(k),

during the subsystems activation time and u(k) = K_i,jx(k),

and i ≠ j,

at the switching instant when system ((1a), (1b)) switches from subsystem i to j. Then the closed-loop switched system becomes

()

Remark 3. From (5a) and (5b) we see that the state impulsive jumping idea is applied since the state feedback controller combines controllers for each subsystem and resetting controller generating a proper state impulsive jumping at switching instant.

Before deriving the conditions for finite-time stabilization of switched system ((1a), (1b)), some explicit facts are recalled. For a symmetric positive definite matrix , it is easy to verify that R can be factorized according to R = (R^1/2) ^TR^1/2, where is a symmetric positive definite matrix. And for any positive definite matrix , there always exist which is positive definite. We present our first result on controller design ensuring the closed-loop system ((5a), (5b)) finite-time stable by following theorem.

Theorem 4. The closed-loop switched system ((5a), (5b)) is finite-time stable with respect to (δ, ε, R, M), if there exist a set of matrices S_i, , X_i,j, , and positive scalars α > 0, β > 0, and γ ≥ 1 such that the following conditions are satisfied :

()

Then the set of state feedback controllers is given by

and

Proof. Let K_i,i = K_i and Substituting X_i,j = K_i,jS_i, into (6a); we get

()

For pre- and postmultiplying (7) by the symmetric matrix

, the following equivalent condition of (7) is obtained:

()

Let

and

in (8); we have

()

Then by Lemma 2 we get

()

Let V_i(k) = x^T(k)P_ix(k),

, for each subsystem of closed-loop ((5a), (5b)); then we construct following Lyapunov-like function:

()

where

and

is the indication function indicating the activated subsystem. In (14), the case i = j shows that the closed-loop system ((5a), (5b)) works in the ith mode described by A_i, and the case i ≠ j implies the closed-loop system ((5a), (5b)) is switching from subsystem i to j at switching instant k, k ∈ {1,2, …, M}. Thus, (10) implies that

()

Applying iteratively (12), we obtain

()

From (11) we know for

and ∀k ∈ {1,2, …, M}

()

where Q_i = R^−1/2P_iR^−1/2,

On the other hand we have

()

using the fact γ ≥ 1 and x^T(0)Rx(0) ≤ δ² we get

()

Using (13), (14), and (16) altogether the following inequality can be derived:

()

Now, to ensure the finite-time stability of closed-loop switched system ((5a), (5b)) with respect to (δ, ε, R, M), the following condition should be satisfied:

()

From (6b) and by Lemma 2, we have

()

then since

, it arrives

()

and from (6c) we have

()

with both (20) and (21) we can obtain

()

which implies (18) is satisfied. Therefore we can conclude that closed-loop switched system ((5a), (5b)) is finite-time stable. Then the proof is completed.

It is worth mentioning that the class of switching signal is not specified during above discussion; thus Theorem 4 supplies us with a sufficient condition for finite-time stability of switched system ((5a), (5b)) under arbitrarily fast switching. We note that the result in Theorem 4 depends on the parameter γ. For a fixed γ, conditions (6a), (6b), and (6c) can be expressed in an LMI form. Obviously, in order to find a suitable γ, a one parameter search may be necessary; nevertheless this does not represent a hard computational problem.

Remark 5. Once the state bound ε is not ascertained, a set of optimized controller gains and with minimum value ε_min⁡ is of interest. Since from (6c) we have ε² > βγ^Mδ²/α, the minimum value ε_min⁡ can be found by solving optimization problem min⁡βγ^Mδ²/α subject to (6a) and (6b). Furthermore, when δ is fixed and letting α = 1, β = κα be derived through optimization procedure according to

()

with a fixed parameter γ and the minimum

, which can be implemented on some numerical optimization software tools such as the optimization toolbox of Matlab to ascertain the optimized value κ and finally ascertain the minimum

. And when the admissible initial state bound δ is not ascertained, a set of optimized controller gains with the maximum δ_max⁡ with a fixed ε is of interest, and the search for δ_max⁡ can be executed by a similar way.

When we let K_i,j = K_i, , the following design results can be derived.

Corollary 6. The closed-loop switched system ((5a), (5b)) is finite-time stable with respect to (δ, ε, R, M), if there exist a set of matrices S_i, X_i, , and positive scalars α > 0, β > 0, and γ ≥ 1 such that the following conditions are satisfied :

()

Then the set of state feedback controllers is given by

Furthermore, if we chose S = S_i, , then we get the following results based on search for a single positive matrix.

Corollary 7. The closed-loop switched system ((5a), (5b)) is finite-time stable with respect to (δ, ε, R, M), if there exist a set of matrices S, X_i, , and positive scalars α > 0, β > 0, and γ ≥ 1 such that the following conditions are satisfied :

()

Then the set of state feedback controllers is given by K_i = X_iS⁻¹.

Obviously, the results in both Theorem 4 and Corollary 6 are based on searching for a set of positive matrices, which would be explicitly less conservative than that based on searching for a common positive matrix in Corollary 7. Moreover, the main advantage of Theorem 4 is that the controller for switched system ((1a), (1b)) designs a reset controller at switching instant, which could reduce the conservativeness compared to Corollary 6 only considering controller for each subsystem. To compare the conservativeness of the above proposed results, a numerical simulation is given in following example.

Example 8. Consider a second order switched system with two subsystems given by

()

We chose

, R = I, and M = 10. Then we assume that ε is not ascertained; our aim in this example is to design the controller ensuring the minimum value ε_min⁡ through optimization procedure (23). In order to illustrate the advantages of our approach based on searching for a set of positive matrices and applying resetting controller at switching instant, three approaches are used.

(1) Firstly we design controller based on searching for a single positive matrix by Corollary 7; the controllers are

()

and the minimum value ε_min⁡ = 7.0739. The simulation result under a random generated switching signal is given in Figure 1. Note that “o” denotes the initial state x(0) and “+” denotes the discrete state x(k), ∀k ∈ {1,2, …, 10}. The solid line denotes the bound for initial state x(0) and the dotted line is the bound for discrete state x(k), ∀k ∈ {1,2, …, 10}.

(2) Then we propose the simulation results by Corollary 6 based on searching for a set of positive matrices but without resetting controller. In this case, we only design controller for each subsystem. The controllers are

()

The minimum value ε_min⁡ = 3.8430. The simulation result is given in Figure 2.

(3) Finally we use the proposed approach by Theorem 4 based on searching for a set of positive matrices and with resetting controller. According to Theorem 4, the controllers are given by

()

The minimum value ε_min⁡ = 3.1179 which explicitly has the smallest value among the three proposed approaches. The simulation result is given in Figure 3.

Comparing three simulation results in this example, we can see that the conservativeness can be reduced by searching for a set of positive matrices and further considering the resetting controller design.

Then we consider the static output feedback controller u(k) = K_iy(k), , and u(k) = K_i,jy(k), and i ≠ j, ; the closed-loop switched system becomes

()

Motivated by the same idea, the output feedback finite-time stabilization will be investigated. At first, the following assumption is given.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

State response and minimum bound by Corollary 7.

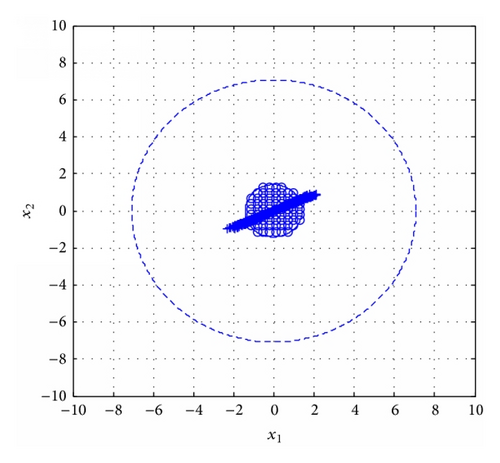
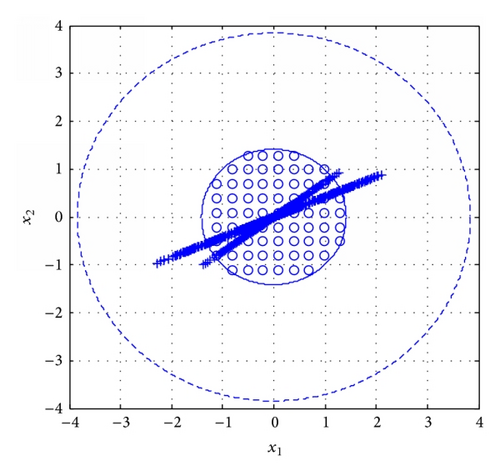
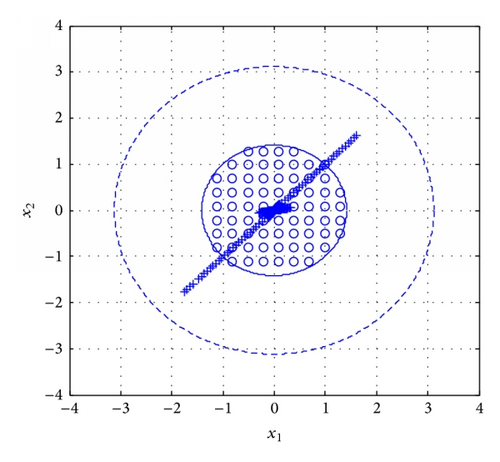
Assumption 9. Matrices C_i, , are full of row rank.

Similar to state feedback controller design and based on Assumption 9, the following result can be derived.

Theorem 10. The closed-loop switched system ((30a), (30b)) under Assumption 9 is finite-time stable with respect to (δ, ε, R, M), if there exist a set of matrices S_i, , X_i,j, , and positive scalars α > 0, β > 0, and γ ≥ 1 such that the following conditions are satisfied :

()

Then the set of state feedback controllers is given by

and

Proof. From (31a) we know that S_i, , are positive matrices, and C_i, , are full of row rank by Assumption 9; it follows that Y_i, , is full of rank and invertible. Thus by (31d), letting K_i,i = K_i and substituting X_i,j = K_i,jY_i we obtain

()

So (31a) is equivalent to

()

For pre- and postmultiplying (33) by the symmetric matrix

, the following equivalent condition of (33) is obtained as

()

Let

and

in (34); we have

()

Then by Lemma 2 we get

()

Let V_i(k) = x^T(k)P_ix(k),

for each subsystem of closed-loop ((30a), (30b)); then we construct the following Lyapunov-like function:

()

where

and

. Thus, (36) implies that

()

Then from (31b) and (31c) and by the same guideline in Theorem 4, we can establish the finite-time stability of closed-loop switched system ((30a), (30b)). Then the proof is completed.

Remark 11. As what is discussed in Remark 3, a set of optimized controller gains and with the minimum ε_min⁡ can be derived through similar optimization procedure according to

()

with a fixed parameter γ and the minimum

4. Finite-Time Stabilization under Slow Switching

In this section, the finite-time stabilization under slow switching is considered. Now we consider a class of average dwell time switching; the definition of average dwell time is given as follows.

Definition 12 (see [13].)For switched system ((1a), (1b)) and any k₂ > k₁ ≥ 0, let N(k₁, k₂) be the number of switchings in the interval [k₁, k₂). If for any given positive numbers N₀ ≥ 0 and τ_a > 0 we have N(k₂, k₁) ≤ N₀ + (k₂ − k₁)/τ_a, then τ_a and N₀ are called average dwell time and chatter bound.

The following closed-loop switched system is considered:

()

Thus, the objective here is to design controller u(k) = K_ix(k),

, ensuring the finite-time stability of closed-loop switched system ((1a), (1b)) with the admissible average dwell time.

Theorem 13. The closed-loop switched system (40) is finite-time stable with respect to (δ, ε, R, M), if there exist a set of matrices S_i, X_i, , and positive scalars α > 0, β > 0, and γ ≥ 1 such that the following conditions are satisfied

()

Then the set of state feedback controllers is given by

Proof. Substituting X_i = K_iS_i, , into (41a) we get

()

For pre- and postmultiplying (42) by the symmetric matrix

, the following equivalent condition of (42) is obtained:

()

Let

in (43); we have

()

Then by Lemma 2 we get

()

Let V_i(k) = x^T(k)P_ix(k),

, for each subsystem of closed-loop (40); then we construct following Lyapunov-like function:

()

where

and

. And by (45) we obtain

()

Similar to the proof line in Theorem 4, from (41b) we get

()

We can easily obtain from (47) that

()

By Definition 12, we get

()

Then let Q_i = R^−1/2P_iR^−1/2,

; we get

()

On the other hand

we have

()

using the fact that x^T(0)Rx(0) ≤ δ² we get

()

Using (50), (51), and (53) altogether, the following inequality can be derived:

()

Now, to ensure the finite-time boundness of switched system (40) with respect to (δ, ε, R, M), the following condition should be satisfied:

()

since we have

()

and from (41c) we have

()

both with (56) and (57) we can obtain

()

Therefore we can conclude that closed-loop switched system (40) is finite-time bounded. Then the proof is completed.

Example 14. Consider switched system with 2 subsystems as follows:

()

We chose ; by Theorem 13 the state feedback controller is designed as

()

and the admissible average dwell time τ_a > 9.9366; thus we chose a periodical switching that the switching occurs every 10 seconds which is shown in Figure 4.

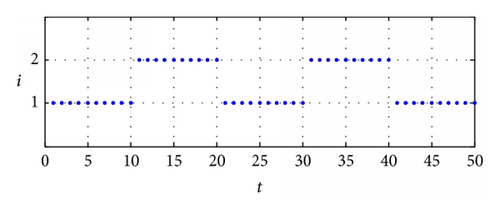
The simulation result is in Figure 5.

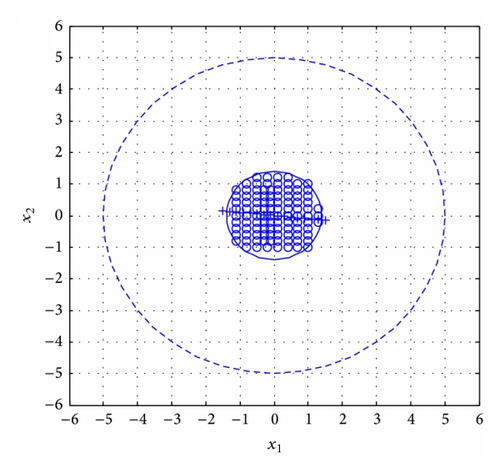
It is explicit that the controller and the switching law with the admissible average dwell time meet requirement of finite-time stabilization.

Then we consider the static output feedback controller u(k) = K_iy(k),

; the closed-loop switched system becomes

()

Similar to the state feedback case, the following results can be derived.

Theorem 15. The closed-loop switched system (61) under Assumption 9 is finite-time stable with respect to (δ, ε, R, M), if there exist a set of matrices S_i, X_i, , and positive scalars α > 0, β > 0, and γ ≥ 1 such that the following conditions are satisfied:

()

Then the set of state feedback controllers is given by

Proof. From the similar guideline in Theorem 10, let , we have

()

Let V_i(k) = x^T(k)P_ix(k),

, for each subsystem of closed-loop system (61); then we construct the following Lyapunov-like function:

()

where

and

. By (63) and (64) we can easily get that

()

Then from the same guideline in Theorem 13, (62b) and (62c) guarantee the finite-time stability of closed-loop switched system (61).

5. Conclusions

The problem of finite-time stabilization for switched discrete-time system is investigated in this paper. Combining the controllers for subsystems and resetting controller at switching instant, the state and output feedback controllers are designed under fast switching. The controller can be obtained by solving a set of LMIs. Then under slow switching, the state and output feedback controllers for subsystems are designed with admissible average dwell time. Several numerical simulations are given to illustrate our approach in this paper.

Conflict of Interests

The authors (Liaoliang Xiao and Mingyang Yu) declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

This work is supported by Hunan Provincial Education Department (no. 13C592).

References

1 Liberzon D., Switching in Systems and Control, 2003, Birkhäuser, Boston, Mass, USA, Systems & Control: Foundations & Applications, https://doi.org/10.1007/978-1-4612-0017-8, MR1987806.
10.1007/978-1-4612-0017-8
Google Scholar
2 Sun Z. and Ge S. S., Switched Linear Systems—Control and Design, 2005, Springer, London, UK.
10.1007/1-84628-131-8
Google Scholar
3 Decarlo R. A., Branicky M. S., Pettersson S., and Lennartson B., Perspectives and results on the stability and stabilizability of hybrid systems, Proceedings of the IEEE. (2000) 88, no. 7, 1069–1082, https://doi.org/10.1109/5.871309, 2-s2.0-33646910241.
10.1109/5.871309
Web of Science® Google Scholar
4 Balluchi A., Benedetto M. D., Pinello C., Rossi C., and Sangiovanni-Vincentelli A., Cut-off in engine control: a hybrid system approach, Proceedings of the 36th IEEE Conference on Decision and Control, 1997, 4720–4725.
Google Scholar
5 Bishop B. E. and Spong M. W., Control of redundant manipulators using logic-based switching, Proceedings of the 36th IEEE Conference on Decision and Control, 1998, 16–18.
Google Scholar
6 Zhang W., Branicky M. S., and Phillips S. M., Stability of networked control systems, IEEE Control Systems Magazine. (2001) 21, no. 1, 84–97, https://doi.org/10.1109/37.898794, 2-s2.0-0034831393.
10.1109/37.898794
CAS Web of Science® Google Scholar
7 Liberzon D. and Morse A. S., Basic problems in stability and design of switched systems, IEEE Control Systems Magazine. (1999) 19, no. 5, 59–70, https://doi.org/10.1109/37.793443, 2-s2.0-0033311181.
10.1109/37.793443
Web of Science® Google Scholar
8 Lin H. and Antsaklis P. J., Stability and stabilizability of switched linear systems: a survey of recent results, IEEE Transactions on Automatic Control. (2009) 54, no. 2, 308–322, 2-s2.0-61349147303, MR2491959, https://doi.org/10.1109/tac.2008.2012009.
10.1109/TAC.2008.2012009
Web of Science® Google Scholar
9 Narendra K. S. and Balakrishnan J., A common Lyapunov function for stable LTI systems with commuting A-matrices, IEEE Transactions on Automatic Control. (1994) 39, no. 12, 2469–2471, 2-s2.0-0028728038, MR1337573.
10.1109/9.362846
Web of Science® Google Scholar
10 Branicky M. S., Multiple Lyapunov functions and other analysis tools for switched and hybrid systems, IEEE Transactions on Automatic Control. (1998) 43, no. 4, 475–482, https://doi.org/10.1109/9.664150, MR1617575, 2-s2.0-0032047505.
10.1109/9.664150
Web of Science® Google Scholar
11 Xiang W., Xiao J., and Iqbal M. N., Asymptotic stability, l₂ gain, boundness analysis, and control synthesis for switched systems: a switching frequency approach, International Journal of Adaptive Control and Signal Processing. (2012) 26, no. 4, 350–373, https://doi.org/10.1002/acs.1287, MR2913645, 2-s2.0-84859786253.
10.1002/acs.1287
Web of Science® Google Scholar
12 Xiang W. and Xiao J., Stabilization of switched continuous-time systems with all modes unstable via dwell time switching, Automatica. (2014) 50, no. 3, 940–945, https://doi.org/10.1016/j.automatica.2013.12.028, MR3173995.
10.1016/j.automatica.2013.12.028
Web of Science® Google Scholar
13 Hespanha J. P., Liberzon D., and Morse A. S., Stability of switched systems with average dwell-time, Proceedings of the 38th IEEE Conference on Decision and Control (CDC ′99), December 1999, 2655–2660, 2-s2.0-0033314314.
Google Scholar
14 Xiang W. and Xiao J., Convex sufficient conditions on asymptotic stability and l₂ gain performance for uncertain discrete-time switched linear systems, IET Control Theory & Applications. (2014) 8, no. 3, 211–218, https://doi.org/10.1049/iet-cta.2013.0409, MR3185346, 2-s2.0-84893961151.
10.1049/iet-cta.2013.0409
Web of Science® Google Scholar
15 Weiss L. and Infante E. F., Finite time stability under perturbing forces and on product spaces, IEEE Transactions on Automatic Control. (1967) 12, 54–59, MR0209589.
10.1109/TAC.1967.1098483
Web of Science® Google Scholar
16 Michel A. N. and Wu S. H., Stability of discrete systems over a finite interval of time, International Journal of Control. (1969) 9, 679–693, https://doi.org/10.1080/00207176908905789, MR0249855.
10.1080/00207176908905789
Web of Science® Google Scholar
17 DAngelo H., Linear Time-Varying Systems: Analysis and Synthesis, 1970, Allyn and Bacon, Boston, Mass, USA.
Google Scholar
18 Amato F., Ariola M., and Cosentino C., Finite-time stabilization via dynamic output feedback, Automatica. (2006) 42, no. 2, 337–342, https://doi.org/10.1016/j.automatica.2005.09.007, MR2195173, 2-s2.0-29244452125.
10.1016/j.automatica.2005.09.007
Web of Science® Google Scholar
19 Amato F. and Ariola M., Finite-time control of discrete-time linear systems, IEEE Transactions on Automatic Control. (2005) 50, no. 5, 724–729, https://doi.org/10.1109/tac.2005.847042, MR2141582, 2-s2.0-20344397953.
10.1109/TAC.2005.847042
Web of Science® Google Scholar
20 Xiang W. and Xiao J., H_∞ finite-time control for switched nonlinear discrete-time systems with norm-bounded disturbance, Journal of the Franklin Institute. Engineering and Applied Mathematics. (2011) 348, no. 2, 331–352, https://doi.org/10.1016/j.jfranklin.2010.12.001, MR2771844, 2-s2.0-79251600177.
10.1016/j.jfranklin.2010.12.001
Web of Science® Google Scholar
21 Xiang W. and Xiao J., Finite-time stability analysis and stabilization for switched linear systems, International Journal of System Science. (2013) 44, no. 2, 384–400, https://doi.org/10.1080/00207721.2011.604738.
10.1080/00207721.2011.604738
Web of Science® Google Scholar
22 Boyd S., El Ghaoui L., Feron E., and Balakrishnan V., Linear Matrix Inequalities in System and Control Theory, 1994, 15, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, Pa, USA, SIAM Studies in Applied Mathematics, https://doi.org/10.1137/1.9781611970777, MR1284712.
10.1137/1.9781611970777
Google Scholar

Citing Literature

All articles

On Finite-Time Feedback Control for Switched Discrete-Time Systems under Fast and Slow Switching

Abstract

1. Introduction

2. Preliminaries

3. Finite-Time Stabilization under Fast Switching

4. Finite-Time Stabilization under Slow Switching

5. Conclusions

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

On Finite-Time Feedback Control for Switched Discrete-Time Systems under Fast and Slow Switching

Abstract

1. Introduction

2. Preliminaries

3. Finite-Time Stabilization under Fast Switching

4. Finite-Time Stabilization under Slow Switching

5. Conclusions

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Related

Information