International Journal of Engineering Mathematics
Volume 2014, Issue 1 426593
Research Article
Open Access

Inviscid Uniform Shear Flow past a Smooth Concave Body

Abdullah Murad, 

Corresponding Author

Abdullah Murad

Department of Mathematics, University of Chittagong, Chittagong 4331, Bangladesh cu.ac.bd

Search for more papers by this author
First published: 23 July 2014
https://doi.org/10.1155/2014/426593
Academic Editor: Shouming Zhong

Abstract

Uniform shear flow of an incompressible inviscid fluid past a two-dimensional smooth concave body is studied; a stream function for resulting flow is obtained. Results for the same flow past a circular cylinder or a circular arc or a kidney-shaped body are presented as special cases of the main result. Also, a stream function for resulting flow around the same body is presented for an oncoming flow which is the combination of a uniform stream and a uniform shear flow. Possible fields of applications of this study include water flows past river islands, the shapes of which deviate from circular or elliptical shape and have a concave region, or past circular arc-shaped river islands and air flows past concave or circular arc-shaped obstacles near the ground.

1. Introduction

Shear flow is a common type of flow that is encountered in many practical situations. Milne-Thomson [1] has discussed inviscid uniform shear flow past a circular cylinder. It should be noted here that in practical situations, objects past which flows occur deviate from regular geometric shapes. In the present paper, we have examined two-dimensional incompressible inviscid uniform shear flow past a smooth concave cylinder. We have obtained a stream function for the resulting flow. It is found that the stream function given in [1] (obtained by using Milne-Thomson’s second circle theorem [1]) for the resulting flow due to insertion of a circular cylinder in a uniform shear flow of an inviscid fluid is a special case of that of the resulting flow past the concave body presented in this paper. Moreover, flow around the same body has been studied for an oncoming flow that is a combination of uniform stream and uniform shear flow. The stream function for each of shear flow past a circular arc or a kidney-shaped two-dimensional body has been calculated from the main result as special cases.

The mathematical results for inviscid fluid flows hold good for flows of common fluids like water and air; the result is valid for the whole region of a flow field except in the thin layer, called boundary layer, adjacent to the body around which the flow occurs. The results of the present study may have applications in many areas of science, engineering, and technology. Here we would like to mention a few particular areas for applications of the present theoretical work, in water flows around river islands, the shapes of which deviate from circular or elliptical shape and have a concave region, noting that rivers have shear flow across and from riverbed to surface; it should be mentioned here that the present results for oncoming flow parallel to line of symmetry of the concave body (i.e., parallel to horizontal axis) can easily be extended to the cases where oncoming flows make arbitrary angles with the line of symmetry. The result for inviscid shear flow past circular arc, obtained here as special case, may find its application in flows past circular arc-shaped islands in rivers. As air flow near the ground is shear flow, the present study may also have applications in scientific investigation of air flow past concave or circular arc-shaped obstacles near the ground.

2. The Shape of the Body

The shape of the body forms owing to inversion of the oblate ellipse by transformation [2]:
(1)
where
(2)
which defines geometrical inversion with respect to the unit circle centered at the point (c, 0) in the z1 ≡ (x1, y1) plane.
Transformation (1) can be conveniently expressed in complex form as
(3)
The two-dimensional body in the inverse plane (z ≡ (x, y) plane) in general has a concave region facing the fluid.
Here the boundary in the z1 plane is an oblate ellipse given by
(4)
A parametric form of (4) can be written as
(5)
where ζ = eiϕ, 0 ≤ ϕ ≤ 2π, in the ζ-plane.
The inverse transformation of (5) is expressed by
(6)
in order that the exterior of the unit circle |ζ| = 1 maps onto the exterior of the ellipse. Moreover, for c > 1 − λ2 and
(7)
the exterior of the ellipse inverts into the exterior of the closed curve in the z plane and vice versa. The equation, obtained from (4) by using transformation (3), that represents the closed curve in the z plane is
(8)
Since corresponding to different values of the parameter λ (4) will represent distinct oblate ellipses, consequently, (8) will also yield distinct smooth closed two-dimensional objects in the z plane for a given fixed c. It is mentioned in Ranger [2] that λ = 0, , and λ = 1 correspond to, in the same order, a circle, a concave body, and a circular arc in z plane; a figure of an object which is a smooth closed curve with a concavity is given in [2], without mentioning any mathematical equation for it. We note that a kidney-shaped body may be obtained for and c = 1 [3] (Figure 1).
Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
(a) Oblate ellipse in z1 ≡ x1 + iy1 plane and (b) kidney-shaped body in z ≡ x + iy plane (found by putting λ2 = 1/2 and c = 1 in (8)).
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
(a) Oblate ellipse in z1 ≡ x1 + iy1 plane and (b) kidney-shaped body in z ≡ x + iy plane (found by putting λ2 = 1/2 and c = 1 in (8)).

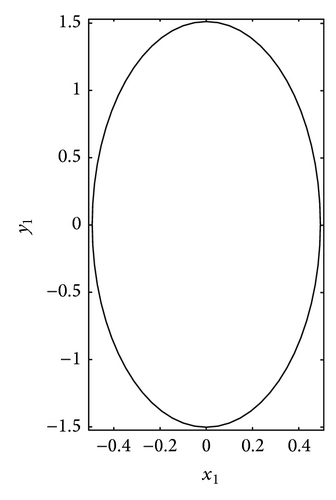
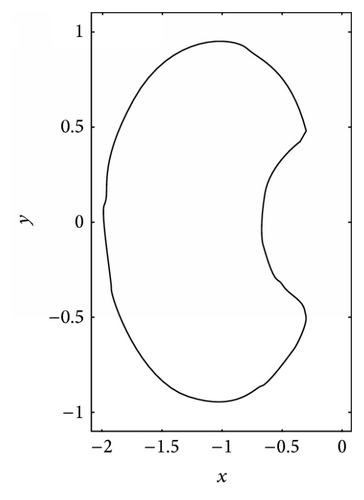
3. Mathematical Formulation and Solution

A uniform shear flow parallel to the x-axis in the z plane, in absence of any boundary, may be expressed by the stream function:
(9)
where ω is the constant vorticity.
The stream function (9) can be mapped onto the z1-plane using transformation (3), which yields
(10)
Again, the mapping of the stream function (10), by utilizing transformation (5), onto the ζ-plane leads to
(11)
where z1 is given by (5) and prime (′) stands for differentiation with respect to ζ.
Now we insert a circular cylinder of radius unity with its centre at the origin, represented by . Since the stream function (11) does not have constant vorticity, we cannot use circle theorem [1] or second circle theorem [1] in order to obtain the resulting flow. In this situation, we propose a formula that will give the resulting flow, and it is
(12)
where and are resulting and basic stream functions, respectively, and is a perturbation stream function.

Since on the boundary of the circle , therefore, becomes zero on the boundary of the unit circle; moreover, becomes the same as as |ζ| → d. If we assume that all the singularities of lie at a distance greater than unity from the origin, then all the singularities of lie inside the circle of radius unity. Regarding , we assume that all the singularities lie inside the unit circle and or a constant on |ζ| = 1 and for |ζ| → d. Thus, the stream function in (12) possesses all the properties to represent the resulting flow.

In the light of (12) the resulting flow for the present case may be written as
(13)
The function Ψ⊗ will be evaluated afterwards in this paper, and we will show that the function satisfies all the conditions that the function must fulfill in accordance with the proposed formula (12).
The flow (13) around the circular boundary can be mapped, by using transformation (6), onto the region outside the oblate ellipse in the z1-plane, which yields
(14)
Again, the flow, given by (14), around oblate ellipse can be mapped onto the region outside the smooth concave body, given by (8), in the z plane by using transformation (3), which leads to
(15)

4. Uniform Shear Flow around a Fixed Circular Cylinder or a Circular Arc or a Kidney-Shaped Cylinder

4.1. Uniform Shear Flow past a Circular Cylinder

For λ = 0, (8) represents a circle in the z plane; the circle is given by
(16)
We put λ = 0 in the stream function (15) to obtain the stream function for flow around the circle (16) as
(17)
The transformation
(18)
gives us the equation of the circle (16) as
(19)
Under transformation (18) the stream function (17) takes the form
(20)
Since there can be no change in the value of vorticity near the cylinder, therefore
(21)
Utilizing (21), on calculation, it is found that in (20)
(22)

Therefore, the result (20) represents uniform shear flow past a circular cylinder, which is in agreement with the known result [1] for the same flow.

The relation (22) implies that
(23)
where
(24)
It is clear from (23) that all the singularities of lie inside the unit circle in ζ-plane (since d > 1), and as ζ → d and (a constant) on the circle |ζ| = 1. Thus, the function Ψ⊗ satisfies all the assumptions that we have made in proposing formula (12), which, therefore, effectively gives the resulting flow due to insertion of a circular cylinder in the flow (11), of which vorticity is not constant.

4.2. Uniform Shear Flow past a Circular Arc

The stream function for uniform shear flow past a circular arc can be obtained by putting λ = 1 (and when λ = 1, c = (d2 − 1)/d) in the stream function (15), which yields
(25)

4.3. Uniform Shear Flow past a Kidney-Shaped Two-Dimensional Body

The stream function for the uniform shear flow past a kidney-shaped cylinder can be obtained by putting λ2 = 1/2 and c = 1 in the stream function (15), which yields
(26)

5. Flow Consisting of a Uniform Stream of Constant Velocity V Parallel to x-Axis and a Uniform Shear Flow Parallel to the Same Axis with Constant Vorticity ω past a Concave Body

Here the basic flow in the z plane is
(27)
Now if we insert the two-dimensional concave body given by (8) into the flow (27), the resulting flow, following an analogous procedure that we have adopted to obtain stream function (15), may be expressed as
(28)
where is given by (15).
The resulting flow due to insertion of a circular cylinder represented by the circle (16) into the oncoming flow (27) can be obtained by putting λ = 0 (and when λ = 0, c = d) in (28) as
(29)
Using transformation (18) (i.e., considering the centre of the circle (16) as the origin of the coordinate system) and with the help of relation (22), the stream function (29) can be written as
(30)
The resulting flow due to inclusion of the circular arc into the basic flow (27) can be obtained by putting λ = 1 (and when λ = 1, c = (d2 − 1)/d) in (28) as
(31)
where is given by (25).
The stream function for resulting flow due to insertion of the kidney-shaped two-dimensional body into the oncoming flow (27) can be obtained by putting λ2 = 1/2 and c = 1 in (28), which leads to
(32)
where is given by (26).

The function Ψ⊗ is given by (23). Therefore, the stream functions (15), (20), (25), and (26) explicitly give resulting flow for the uniform shear flow past a concave body, a circular cylinder, a circular arc, and a kidney-shaped body, respectively. And stream functions (28), (29), (31), and (32) explicitly give the resulting flow around a concave body, a circle, a circular arc, and a kidney-shaped body, respectively, where in each of the cases the oncoming flow is the combination of the uniform stream and the uniform shear flow.

6. Conclusions

In this work, we have obtained a stream function in complex variables for inviscid uniform shear flow past a two-dimensional smooth body which has a concavity facing the fluid flow. It is found that the result for the same flow past a circle that is deduced from the central result as a special case agrees completely with the known result. Also, stream functions for the same flow past a circular arc or a two-dimensional kidney-shaped body are evaluated.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

The author would like to thank Professor Dr. S. K. Sen (retired) of Jamal Nazrul Islam Research Centre for Mathematical and Physical Sciences, University of Chittagong, Bangladesh, for valuable discussions during preparation of this paper.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.