Flow accelerated corrosion (FAC) of carbon steels in water has been a concern in nuclear power production for over 40 years. Many theoretical models or empirical approaches have been developed to predict the possible occurrence, position, and rate of FAC. There are a number of parameters, which need to be incorporated into any model. Firstly there is a measure defining the hydrodynamic severity of the flow; this is usually the mass transfer rate. The development of roughness due to FAC and its effect on mass transfer need to be considered. Then most critically there is the derived or assumed functional relationship between the chosen hydrodynamic parameter and the rate of FAC. Environmental parameters that are required, at the relevant temperature and pH, are the solubility of magnetite and the diffusion coefficient of the relevant iron species. The chromium content of the steel is the most important material factor.

1. Introduction

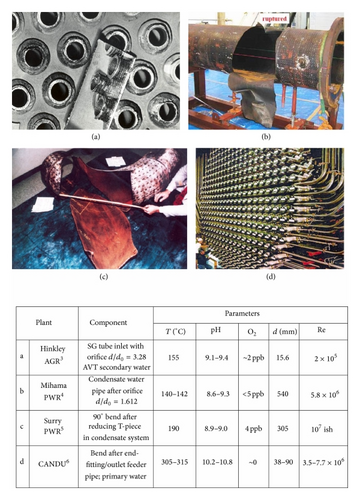
Flow accelerated corrosion (FAC) of carbon steels in water has been a major concern in civil nuclear power production for over 40 years [1, 2]. The important features of FAC are the linear or increasing rate with time and the generation of a scalloped surface. Its effects have been unique in two important ways. Firstly it has affected nearly every reactor type worldwide and sometimes in more than one location; Figure 1 shows some examples [3–6]. Secondly it is probably the only corrosion mechanism that has led to accidents that have caused fatalities. There have been pipe ruptures leading to a release of steam and deaths of workers, but it must be emphasized that such fatalities are not unique to nuclear plants.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Examples of FAC in nuclear power plants.

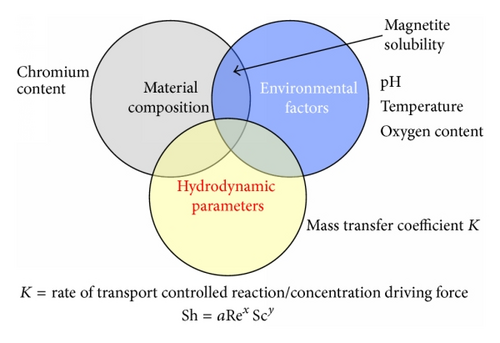
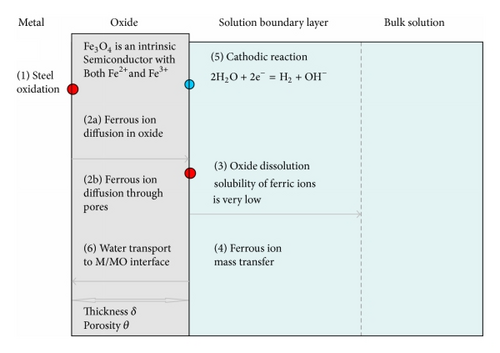
The occurrence of FAC, or erosion corrosion as it is sometimes known, is critically dependent on the following: the temperature and chemistry of the environment (pH and oxygen content), the hydrodynamics of the system, and the composition of the steel particularly the chromium content; this is shown schematically in Figure 2.

There are various approaches to predicting the possibility and the rate of flow accelerated corrosion. Testing has involved either actual components or a chosen specimen. In addition there are theoretical or empirical models, some computer based, available to allow the prediction of attack.

It is readily apparent that any review must be very selective; other reviews are available [7–10]. This review has tried to cover areas that the author has been involved with over the last 40 years that have been neglected or are contentious. It follows earlier reviews [11–14] but focuses on FAC of steels in the nuclear power plant industry. For both practical and mechanistic reasons there is a need to identify the hydrodynamic parameter which controls the occurrence and rate of erosion corrosion. It was previously suggested [12] that there was a spectrum of mechanisms which could be involved in erosion corrosion. This review concentrates on the corrosion end of the spectrum. It is argued that for dissolution based mechanisms the important hydrodynamic parameter is the mass transfer coefficient (K). The relationship between the rate of FAC and K is discussed in some detail and the development and effect of surface roughness on both K and FAC are considered. Finally some aspects of the solubility of magnetite and the prediction and prevention of FAC are discussed. This review is not a best buy guide to predictive programs.

2. Hydrodynamics

The various hydrodynamic parameters that have been credited with controlling the occurrence and rate of flow assisted corrosion are as follows.

(i)
Velocity (V).
(ii)
Reynolds number (Re).
(iii)
Mass transfer coefficient (K).
(iv)
Surface shear stress (τ).
(v)
Intensity of turbulence (TI).
(vi)
Freak energy density (FED).

An attempt to describe how each of these parameters might be measured is given in Table 1. It is widely accepted that it is neither the velocity nor the Reynolds number that is critical. Both the surface shear stress and the mass transfer coefficient are widely believed to be important. The former in the oil and gas field the latter in the power generating industry. But recently τ has gained some devotees [15] in the power generating industry. However there are some workers [16] who believe the following.

The mass transfer coefficient is intimately linked to wall shear stress, and the two cannot be practically separated either experimentally or mathematically [16].

Table 1. Possible important parameters and some measurement techniques.

Parameter	Some measuring techniques	References
The velocity (V).	(i) Calculated from flow rate and flow area (ii) Ultrasonic sensors (iii) Pitot tube	[11, 17, 18].

Reynolds number (Re).	Calculated from velocity, diameter of tube, and kinematic viscosity	[11, 17, 18].

Mass transfer coefficient (K). Requirements: (1) Use of realistic geometries (2) Measurement of both smooth and rough surfaces (3) Use in two-phase flow	(i) Dissolution of sparingly soluble solid (ii) Limiting current (iii) Analogy with heat transfer (iv) Computational	[12, 19–23].

The surface shear stress (τ). Requirements as for K	(i) On isolated surface element using force transducer (ii) Pressure drop (iii) Various types of heat transfer sensors (iv) Limiting current density on isolated small electrode, but not for separated flows (v) Computational	[12, 18–20, 24, 25].

Intensity of turbulence (TI). Requirements as for K	(i) Analysis of fluctuations in limiting current density on isolated small electrode. (ii) Hot wire (iii) Laser-Doppler anemometer	[11, 18–20].

Freak energy density (FED). Requirements as for K	Complex analysis of fluctuations in limiting current density on isolated small electrode, single author use.	[26–28].

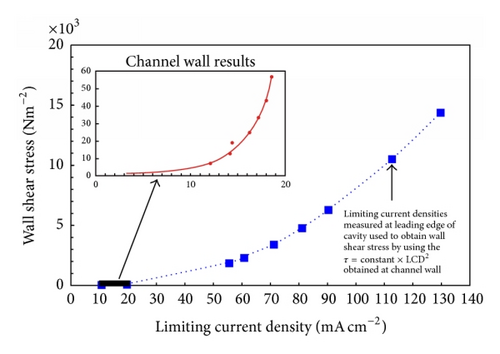
This view has been challenged by a number of workers [25, 29] based on the breakdown of the analogy between mass, heat, and momentum in detached flow. The consequences of this are that in detached flow the surface shear stress cannot be calculated from the measured limiting current density (LCD) at an isolated microelectrode, where in normal flow τ is proportional to the cube of the limiting current density (Leveque equation); this is demonstrated in Figure 3. This problem seems to have been ignored by Schmitt and Gudde [30] whose approach was to obtain a functional relationship between shear stress and limiting current density for a normal flow situation (Figure 4). Then to use the same relationship to convert LCDs measured in disturbed flow to shear stresses (Figure 4). Apart from being invalid this approach involved the extrapolation of a maximum shear stress in the channel wall of under 60 N/m² to over 14000 N/m² in the disturbed flow.

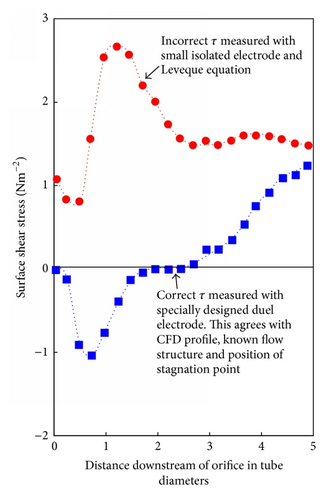
One way of refuting the importance of τ is its variation, for example, downstream of an orifice where the FAC and shear stress profiles are fundamentally different (see Figures 3 and 5). This refutation of the importance of τ has apparently been misunderstood [32]. A similar rejection of the dominant role of τ has been made by Matsumura et al. [33, 34] in work with an impinging jet. Another reason to believe that τ is unimportant is because it seems that the surface shear stress is not sufficient to produce the effects ascribed to it, namely, mechanically disrupt a surface film.

For copper alloys in seawater Matsumura showed that the FAC profile did not correspond to the measured shear stress distribution on an impinging jet specimen but could be explained by the forces, measured with a pressure transducer, due to the peak in turbulence intensity at about 2 jet diameters from the centre of the specimen. Of course mass transfer is caused by bulk convection and turbulent convection, so while ruling out the primacy of the importance of shear stress this does not prove the importance of mechanical factors. It must be remembered that increased mass transfer can dissolve away a protective surface layer; this was elegantly analysed by Coney [35].

Schmitt and Mueller initially proposed [36] a fatigue based model for oxide failure, and it is not clear to this author why such an approach was apparently rejected for the freak energy density (FED) model. Although this was applied to the oil and gas industry [27] his ideas have been published in power plant chemistry [28] and thus warrant discussion. The FED model is conceptually similar to Matsumura’s view on the importance of the turbulent flow generating high local stresses.

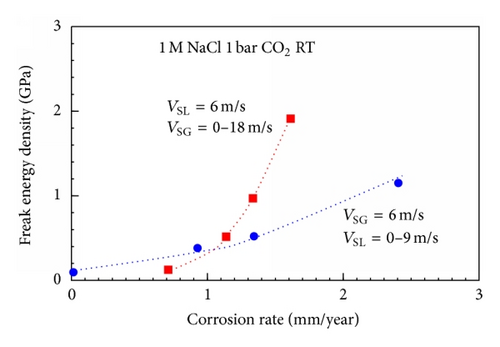
It was found that forces in high energy microturbulence elements oriented perpendicularly to the wall are finally responsible for the scale destruction (freak energy density (FED) Model). The maximum FED in a flow system can be measured with appropriate tools; however, in practical cases this is not necessary, because in a given flow system the FED is proportional to the wall shear stress by a factor in the order of 10⁵ to 10⁶. Thus, for practical application and flow system evaluations wall shear stresses can be used to quantify flow intensities in given flow systems [27].

FED is a derived freak value from measuring the noise in the limiting current density (LCD) on isolated small point electrodes (ISPE). It appears [27, 28] that this is a complex process involving wavelet transforms, simulations, and phasing in of waves. The net result is a freak current density; values of as high as 500 A cm⁻² have been quoted. The energy density of a freak wave volume element accelerated towards the surface can be expressed according to classic wave dynamics from

()

where w is energy density (Pa), ρ is density (kg/m³), A is wave amplitude (m), and ώ is wave frequency (s⁻¹). Both energy density and wall shear stress have the unit Pascal in common. It was, therefore, assumed that the same relation used in the Leveque equation can be used to calculate the freak energy density from the freak current density. For the freak current density of 500 A cm⁻² a freak energy density of 3 GPa was derived.

Such an approach can be questioned on a number of important points.

(1)
Although there are time response limitations involved in LCD measurements it might be expected that some freak events could at least be partially detected, after all real freak waves can be observed.
(2)
No attempt to measure such high stresses was made, for example, by fast response pressure transducers, as Matsumura did.
(3)
The use of the Leveque equation to obtain freak energy densities from freak current densities is highly questionable.
(4)
There is not a single relationship between τ and FED [27, 28] and from a practical point of view this would have to be obtained for each geometry of interest. And measuring surface shear stresses in detached flow is, as outlined earlier, not possible using Schmitt’s technique.
(5)
How rough surfaces that develop naturally during corrosion are dealt with is unclear.

Also as yet there has been no data that supports the use of FED to predict FAC, indeed Figure 6 from a 2009 paper [27] appears key since it suggests that there is not a single relationship between corrosion rate and FED, for two different flow conditions, in the same environment. Finally there is a mechanistic problem in what exactly happens when a surface layer is cracked; Schmitt has suggested the following.

Once removed the high local flow intensities prevent the re-formation of protective layers and, hence, start fast mass transport controlled local metal dissolution (FILC, also called erosion corrosion).

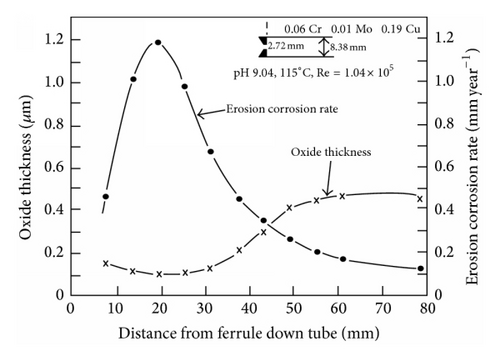
For steels in pure boiler water there is good evidence that the protective magnetite layer is thinned (not cracked) and the FAC rate correlates with this thinning [31] and the mass transfer coefficient (Figure 5). There is also the possibility that the mass transfer could be large enough to lead to the film being completely removed by dissolution. In this case the subsequent rate of attack would probably be limited by activation kinetics. This film dissolution appears to have occurred on carbon steel exposed to sodium nitrate solutions under an impinging jet [11].

Of course in most situations in which corrosion is occurring the surface undergoes some roughening; this then raises the question of how to measure the changes in the hydrodynamic parameter as the roughness develops. Roughness development and other considerations (Table 1) led the current author to develop, justify, and apply the dissolution of copper in ferric chloride solutions [21, 37–41] (Figure 7), to the measurement of mass transfer coefficients; typical specimens from single-phase and two-phase studies are shown in Figures 8 and 9.

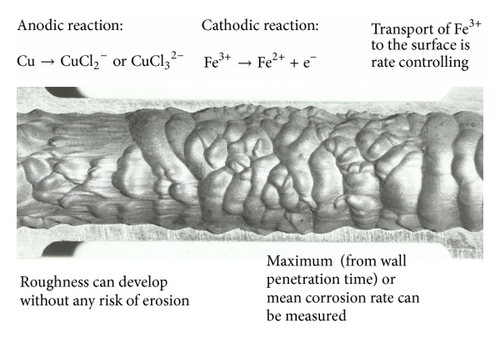
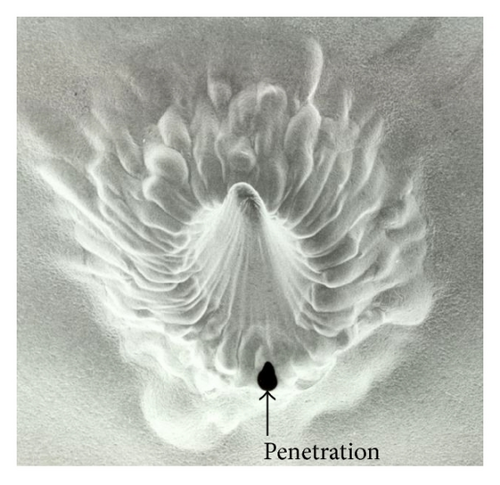
Because some predictive models use an enhancement factor to describe a geometries effect relative to a straight tube such a factor is often quoted. It must be emphasised that this factor is usually a function of the Reynolds number and its use has nothing to do with—the mass transfer coefficient at the point of interest becomes difficult to measure or even define, so “enhancement factors” over the straight-pipe values are employed [32].

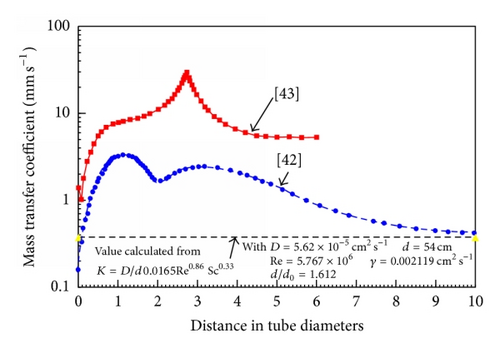
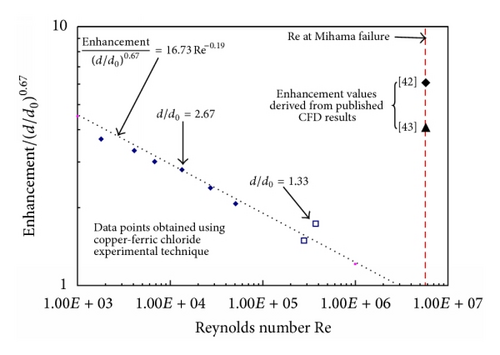
Recently there has been an increasing tendency to use computation fluid dynamics (CFD) techniques to obtain hydrodynamic parameters for subsequent use in FAC assessments. CFD has the ability to investigate very high Re’s, which often cannot be reached in experimental studies. However CFD results must be shown to agree with well established data before it can be applied to the higher flows. A number of applications of CFD are listed in Table 2; unfortunately some of these computations have been carried out without any comparison to well established experimental data; in some cases there are significant differences. This is particularly evident after the Mihama-3 FAC failure downstream of an orifice; the mass transfer characteristics of which have been studied by a number of workers and reviewed by others. Figures 10 and 11 are a summary of and comparison with excepted correlations. The difference between the two CFD predictions is of some interest; the higher results may be a misprint in units, as the other data agrees very well with a simple calculation for fully developed flow. It is of great interest that the CFD predicted enhancements are much higher than those from expected correlations downstream of an orifice, yet no comparison with the well established lower Reynolds number data were made. Also in this authors’ view CFD has not been shown to be capable of modelling the roughness and its effects that develops naturally by metal dissolution or oxide deposition.

Table 2. Examples of the use of CFD in FAC.

Authors	Purpose	Comments	References
Uchida et al.	Prediction of FAC with Mihama as test case	No comparison with existing data and its extrapolation to high Re’s or effects of roughness	[42]

Hoashi et al.	Prediction of FAC with Mihama as test case	No comparison with existing data and its extrapolation to high Re’s or effects of roughness.	[43]

Pietralik and Smith, Pietralik and Schefski	Prediction/explaining CANDU feeder FAC	Compares with some but not all bend data. Attempts to deal with roughness development and component interactions	[44, 45]

Nesic and Postlethwaite	Predict e-c following sudden expansion	Makes key point that profiles of K and shear stress do not correlate	[29]

Zinemams and Herszaz	Predict FAC in bifurcation and nozzle	Limited detail to check results but claims there is agreement, effects of roughness not considered.	[46]

Yoneda	Predict FAC in PWR and BWR, of 45° elbow	Interesting but again no comparison with others or the effects of roughness	[47]

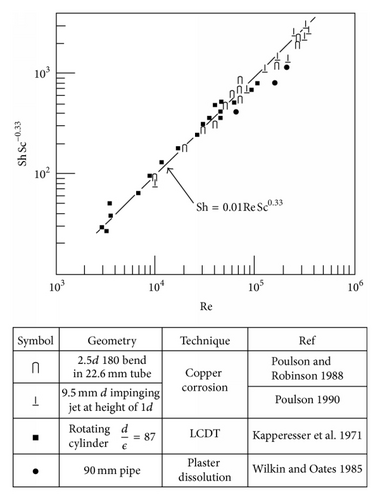
Roughness development in situations where a solid is dissolving under mass transfer control has been investigated by a number of workers. One theory attributes roughness to the imprinting of the fluid on the surface [48] and the other to the role of surface defects [49]. Criteria for the development of roughness have not been fully developed and it is perhaps overlooked that there is a tendency for leveling of any surface which is dissolving under diffusional control [39]. For example, consider an isolated roughness element exposed to single phase flow. It would be expected that the rates of dissolution of both the peak of the roughness element and the region after the roughness element were both higher than the region upstream. For roughness to develop the region after the roughness peak must dissolve faster than the roughness peak itself. In two phase flow it is probable that the annular film would leave the wall after the peak rather than inducing separated flow as in single phase conditions. Thus it would seem reasonable that in annular two-phase flow roughness development would be more difficult and would tend to occur only when the thickness of the wall film was such that a recirculation zone could form.

It is the effect of roughness that is of general relevance, and our findings [37–41] can be summarized as follows.

(1)
While defects can produce surface roughness, they are not a requirement. The roughness that develops usually reflects the flow structure. For example, Figure 7 illustrates the symmetrical peaks at the inlet to the 180° bend and evidence of counter rotating vortices in the bend region.
(2)
There appears to be a critical Re required for roughness to develop. The critical Re value ~5 × 10⁴ in 8 mm diameter tubing [40] is significantly higher than that found using dissolving plaster of Paris [22], where roughness developed at the lowest Re tested of 1.9 × 10⁴ in 25 mm diameter tubing.
(3)
There are other indications [39] that using the dissolving plaster of Paris technique can give misleadingly high values of K due to erosion of the plaster occurring.
(4)
If the surface roughens the mass transfer can increase and there are indications [40] that the roughness becomes more important then than the geometry in influencing mass transfer.
(5)
An upper bound mass transfer correlation for all rough surfaces has been proposed [38] as shown in Figure 12:
()
(6)
There is some evidence, Table 3 [41], that the development of roughness has a smaller effect on geometries where flow is separated, as compared to normal flow. In the former turbulence is generated away from the wall, while in normal flow it is generated close to the wall. This was first realized with the region downstream of an orifice in that some enhancement in mass transfer occurred in some tests but again nowhere near a Re_o dependency (Figure 10). Also for a multi-impinging jet and a cylinder in restricted cross flow the rough surface mass transfer correlations all have a Reynolds number dependency with an exponent less than one, Figure 13, with
()
(7)
If roughness develops, the height (ε) and wavelength (λ) of the roughness elements decrease with increasing Re [40]. This means that the enhancement in mass transfer caused by roughness does not increase with increases in ε/d. There is a suggestion [50] that the roughness that develops at any Re produces the maximum resistance to flow.
(8)
If roughness develops the enhancement factor of any geometry over a straight tube is not a constant [37] and will usually increase with the Reynolds number. For the region downstream of an orifice the enhancement decreases with increases in Re for both smooth and rough surfaces.

In summary the initial surface roughness (or defects) will influence the subsequent development of dissolution induced roughness which will occur at lower flow rates for rougher initial surfaces. However the final or equilibrium roughness that develops as a result dissolution will probably be largely dependent on the flow rate, with smaller scallops as the Reynolds number increases. The effect of roughness developing, in increasing the rate of mass transfer and thus the rate of FAC, is expected to be less for geometries where flow separation or detachment occurs.

Table 3. Differences between normal and separated flow.

	Normal flow	Separated flow
Shear stress and K	Related	Not related
Turbulence created	Near wall	Away from wall
Roughness effects on K and ΔP	Both increase	Evidence for increase lacking
Roughness effects on FAC	Limited clear evidence of increase	Evidence for increase lacking

But in all probability there will be a number of situations that are between these two extremes.

In two-phase flow it is not immediately obvious how the mass transfer data can be simply incorporated since there is some evidence [39] that Chen’s correlation is not valid. Figure 14 shows a simple model can apparently be used to relate the tightness of bends to the resulting influence of the annular flow on the mass transfer at bends. There is evidence that mass transfer effects dominate at least up to 50 m s⁻¹; but clearly mechanical damage will occur above some critical velocity which needs to be defined; this leads to the concept of a spectrum of mechanisms as suggested earlier [12]. Models ascribing droplet impingement causing mechanical damage are referenced later in predictive models but are outside the scope of this paper.

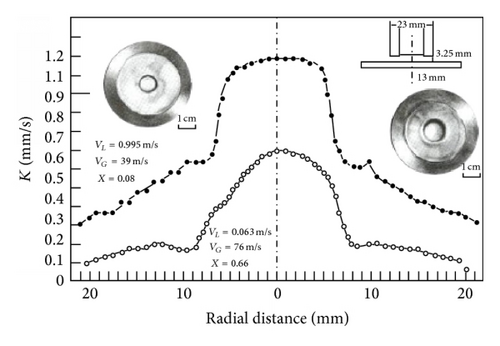
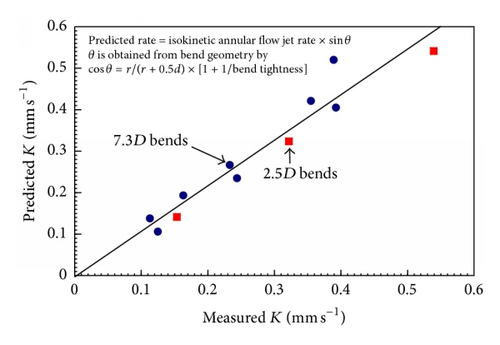
The relationship between K and FAC must not be assumed to be linear; this is discussed later in this review.

3. Environmental Variables

It is widely accepted as shown schematically in Figure 1 that the three most important environmental parameters influencing the occurrence and rate of FAC are as follows.

(i)
Temperature.
(ii)
pH.
(iii)
Oxygen content.

These have been discussed in detail and further discussion is beyond the scope of this review. However each of these variables probably exerts their influence through their effect on the solubility of magnetite. It is believed that this has been a neglected topic. For example in one of the first reported cases of FAC at 300°C it was suggested [51] to be the result of high mass transfer and low Cr content in the steel with little consideration to the reduced solubility of the magnetite at that temperature. A similar situation occurred in a recent paper [52] describing low temperature FAC.

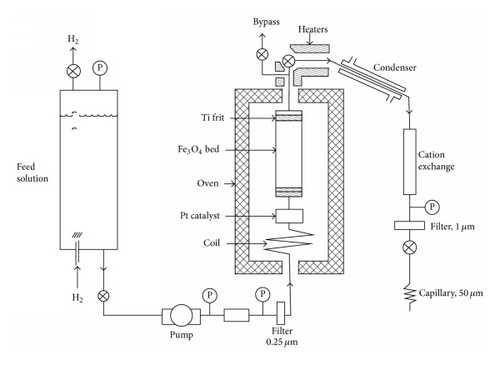
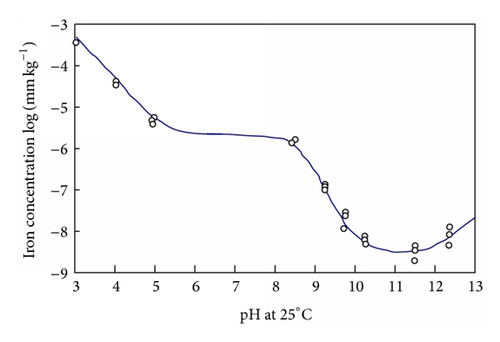
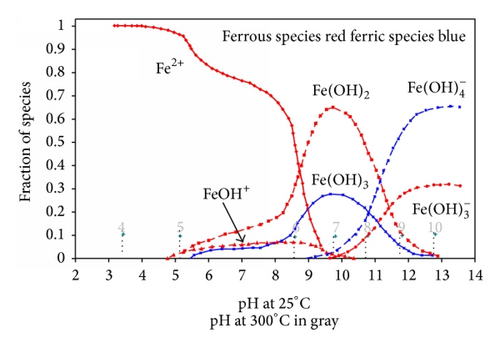
In general solubility’s can be calculated from available thermodynamic data or measured. For a very sparingly soluble oxide like magnetite the preferred option has been to experimentally determine it using equipment such as that shown in Figure 15. There are a number of experimental difficulties such as the need to establish steady state conditions under controlled redox conditions, the problems with colloidal material, and the influence of trace impurities. Such solubility data, for example, Figure 16, is then used to obtain thermodynamic data for the various possible dissolving species, for example, Figure 17. The total solubility of iron species can then be modeled and predictions can be made (Figure 18).

From an examination of the key papers [53, 55–58] there are certain key facts, some are well known, for example, 1 and 2, and form the basis of controlling of deposition in primary circuits, others are not, yet they could significantly influence the ability to predict FAC.

(1)
The gradient of solubility with respect to pH changes from negative to positive at a critical pH, producing a typical U-shaped curve, Figure 16. The pH value this occurs at is of intense interest; an estimate (using T&LeB data [53]) can be obtained from
()
(2)
The gradient of solubility with respect to increasing temperature changes from negative at lower pH to positive at higher pH, Figure 18; this occurs at ~9.4 and 9.9 at temperatures of 300°C and 150°C, respectively [53].
(3)
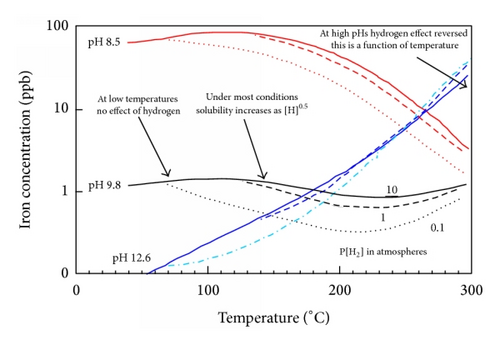
There are various functional relationships between iron solubility and hydrogen content which arise because of the details of the stable species and the nature of the oxide dissolution reaction, Table 4 and Figure 18.
- (i)
  Usually [53, 56] the solubility is proportional to :
  ()
- (ii)
  As pHs increases the solubility is predicted [53] to become proportional to , and that will occur above a certain temperature [55]. Consider
  ()
  However the data appears to be insufficient to make accurate predictions of pH’s and temperature’s and the expectation is that the transition will be gradual.
- (iii)
  Solubility is independent of [H₂] at low temperatures below ~83°C [55]. But this temperature increases with increases in [H₂]. This is due to the activity of ferrous ions in solution being controlled by a hydrous ferrous oxide phase rather than magnetite [55].
(4)
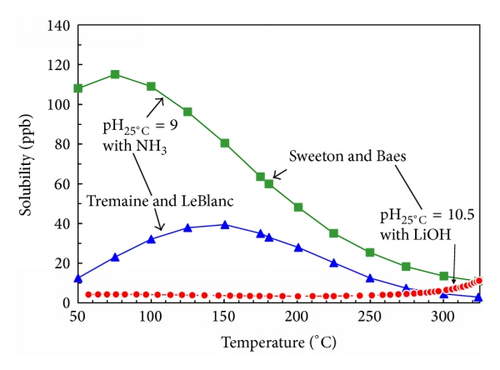
There appear to be significant differences between the two most quoted data sets as shown in Figure 19. In particular the values of Tremaine and LeBlanc (T&LeB) are lower than those of Sweeton and Baes (S&B) and mirror the temperature dependency of FAC more closely.
(5)
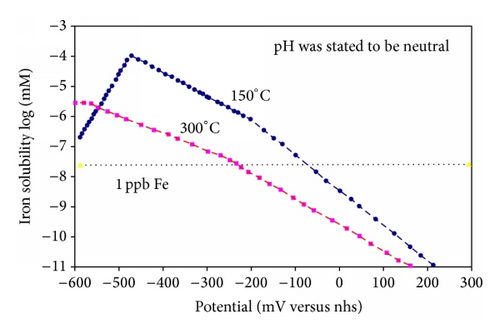
Under conditions where ferrous ions are dominant the effect of potential [59], Figure 20, or oxygen content of the water is profound and of great practical importance; the solubility of haematite is exceedingly small.
(6)
There is no solubility data available for magnetite containing chromium; such data might allow the role of chromium to be clarified.

There are different functional relationships between pH_RT and pH_HT for ammonia, morpholine, ethylamine, and lithium hydroxide, which depend on basicity, volatility, temperature, and steam quality which need to be considered; this has been discussed recently by Bignold [60].

Table 4. Possible variations in magnetite solubility dependency on hydrogen concentration.

Regiem	Hydrogen dependency	Reference
Normally	[H]^1/3	[53, 55, 56]
At high pHs above ~220°C	[H]^−1/6	[53, 55]
At temperatures below ~80–110°C	Independent	[55]
At high temperatures above pH~9.8	Less than [H]^1/3	[55]

Such effects could influence both dissolution and deposition.

As indicated earlier another important parameter influenced by the environment is the diffusion coefficient (D) of the relevant dissolving iron species. This is rarely discussed, either the value utilized or how it was obtained. One of the few relevant discussions was presented by Coney [61]; it was indicated that there were a number of possible dissolving ions, and diffusion coefficients were calculated using both anionic and cationic data. As Newman [62] and others [12] have pointed out it is the ionic diffusion coefficient (cm²/s) which should be calculated using the Nernst-Einstein equation:

()

where R the universal gas constant is 8.3143 J mole deg, λ means the ionic equivalent conductance is in ohm-cm²/equiv, T is the temperature in degrees Kelvin, n is the charge on the ion, and F is Faraday’s constant 96,487 C/equiv. The effects of temperature are usually calculated using Stokes-Einstein equation or Wilkes rule (Dμ/T = constant) and this has been compared to an activation energy approach and found in reasonable agreement [12].

In Figure 21 the results of Coney are shown and compared to the recalculated values for FeOH⁺, which Coney suggests is the most relevant species. It appears that the recalculated values are approximately half of the earlier values and a correlating equation obtained using Table Curve^* is given.

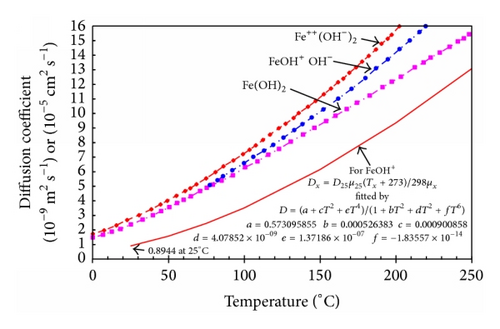
Temperature also influences the density and viscosity of water; such values are readily available in the literature.

4. Material Influences

It has been known for some considerable time that the chromium content of steel [63, 64] has an important role in influencing flow accelerated corrosion; typical results are shown in Figures 22 and 23. There is some evidence [63] that under some situations copper and molybdenum may also be beneficial. Suggested correlations for the fractional reduction (FR) in FAC caused by alloying include

()

It is of considerable interest that welds can have weld metal lower or higher in chromium than the parent metal; this needs to be considered in any assessment.

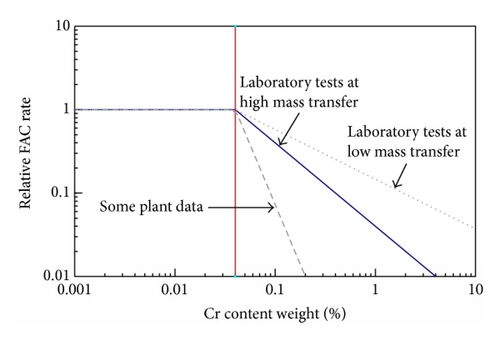
In general water chemistry changes are so much easier to implement than material changes; it is only in new or replacement components that material changes can be made.

It is believed that the first instance when the possibility of FAC influenced, indeed determined, the choice of material (1%Cr1/2%Mo) was for the economizers for the British advanced gas cooled reactors (AGRs) once through boilers at Torness and Heysham 2. This was substantiated by long term tests (22800 hour) in laboratory rigs, on-site rigs, and in situ SGs exposure. Both tight 180° bends and orifice geometries were utilized, Figure 24. Interestingly the feedwater system for the British PWR at Sizewell, ordered later, was specified as carbon steel. While there is no dispute as too the benefits of chromium additions there have been at least three suggestions as to its mechanism.

(i)
It slowly enriches at the dissolving magnetite surface and limits the solubility [66, 67].
(ii)
It alters the kinetics of oxide dissolution, possibly after enriching at the surface [68].
(iii)
It changes the oxide porosity [69].

5. Predictive Approaches

5.1. Testing

There are two possible approaches. The first is to test all geometric features of interest under realistic and accelerated conditions to obtain margins of safety. Figure 24 shows such a rig used to test AGR components at design and twice design velocities for times up to 22800 hours.

The alternative approach is to use a specimen with a range of mass transfer rates as illustrated in Figure 25, or a single specimen over a range of flow rates. In all cases it is good practice to check any relationship, between the suspected hydrodynamic parameter and the rate of FAC, with tests using a different specimen geometry.

The author can see no point in using a specimen for which there is no mass transfer data available. It is important in all cases to ensure the following.

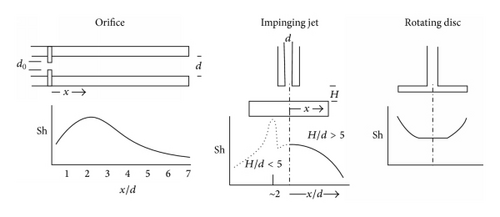
(1)
Tests are carried out long enough to obtain realistic steady state rates.
(2)
The method of measuring the corrosion rate has the required precision; various methods have been suggested [12].
(3)
The environmental conditions in the test rig really do correspond to the practical situation. The use of a marker geometry, that is, one which corrodes at a known rate, has much to commend itself.

The advantage of the first approach is that real components can be tested and the dependency between corrosion rate and mass transfer will be established if the latter is known. It must be emphasized that this might change if the environmental conditions change. The advantage of the second approach is that it might prove possible to obtain the FAC versus K relationship with a single specimen where high precision measurements are possible. One difficulty in using specimens is that the development of roughness can be significantly different between geometries. The specific example of using small diameter tubes to obtain data relevant to large diameter pipes has been covered in some detail [40].

5.2. Theoretical Based Models

There appears to be reasonably widespread agreement that the basic mechanism of FAC is the enhanced transport of dissolved ferrous ions away from the metal surface. This causes the protective magnetite film to be thinned down and results in essentially linear kinetics. This is to be compared to parabolic kinetics during normal corrosion.

The simplest formulation of an FAC model gives the corrosion rate as the product of the mass transfer coefficient (K) and the solubility driving force (ΔC), where ΔC is difference between the solubility and the bulk solution level:

()

K is usually obtained from correlations of the general form

()

where Sh (the dimensionless mass transfer Sherwood number) is given by K(d/D).

Re (the dimensionless Reynolds number) is given by V(d/γ) and Sc (the dimensionless Schmitt number) is given by γ/D.

V is the relevant velocity (m s⁻¹), d is the characteristic specimen length (m), γ is the kinematic viscosity (m² s⁻¹), and D is the diffusivity of the relevant species (m² s⁻¹).

Substituting for K,

()

So in principal, if the mass transfer is known and the concentration driving force is known, the only other parameters required are the diffusion coefficient of the relevant ionic species and the appropriate kinematic viscosity.

However, most if not all the predictive models involve additional processes shown in Figure 25. The differences in the various mechanistic models arise in the way the processes are quantified and combined, in particular in the explanation of the key environmental parameters especially the temperature and how the flow dependency of the measured FAC rates can be explained.

From a predictive aspect a very important difference is that some theories predict a linear relationship between mass transfer and flow accelerated corrosion rate: a nonlinear rate is predicted by other models particularly the CEGB theory of Bignold, Garbett, and Woolsey. Other workers have argued that a greater-than-linear dependency of rate on mass transfer equates to a mechanical contribution probably in removing oxide.

The CEGB model [10, 54, 66, 67, 70, 71] (Bignold, Garbett, and Woolsey) was developed because the maximum FAC rate and the measured FAC profile downstream of an orifice could not be explained by the available magnetite solubility data, and a linear relationship between FAC and mass transfer. In addition to explain the decrease of FAC at lower temperatures, it was postulated that the rate of magnetite dissolution (R of Fe₃O₄ dissolution) controls the rate of FAC at low temperatures:

()

There is strong evidence that the solubility of magnetite is a function of the hydrogen content of the water. Thus it appears that the process could be self-accelerating in that the higher the corrosion rate is, the more hydrogen is produced locally, and this could enhance the solubility of the magnetite. An electrochemical model was developed which indicated that the solubility of magnetite could be proportional to the square of the mass transfer coefficient.

Thus the FAC rate could be proportional to the cube of the mass transfer coefficient, or in general with n being a variable between 1 and 3:

()

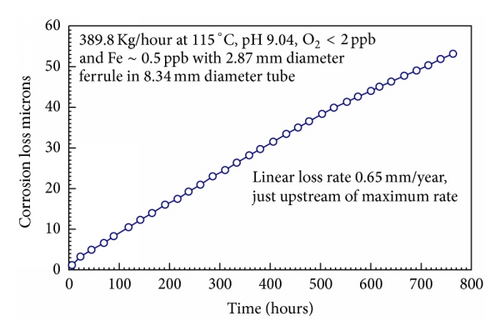
High resolution measurements of the FAC rate downstream of a ferrule or orifice suggested that the rate did not increase with time as the surface roughened, Figure 27, and roughness effects do not appear to have been incorporated into the CEGB model.

The EDF model [65, 69, 72–76] has been developed with a number of modifications, most importantly the incorporation of the oxide porosity θ, oxide thickness δ, and k the rate constant for magnetite dissolution as important parameters. The original formulation in 1980 was

()

From which one gets

()

Then this was modified, after the Sanchez Calder model to take account of oxide porosity:

()

And if mass transfer is the rate controlling step [1/k ≪ 0.5(1/K + δ/D)] and for thin oxides (1/K ≫ δ/D) this reduces to

()

The solubility of magnetite is obtained from Sweeton and Baes. Mass transfer coefficient is obtained by using a straight tube correlation modified for surface roughness and an enhancement factor to account for the component geometry:

()

Early versions of their model appeared to explain the variation of FAC with temperature and alloying effects, particularly the effect of chromium, by varying the values of oxide porosity θ and thickness δ. In the latest description of the model, the following is stated [65].

The porosity behavior with temperature is difficult to model. It appears to be temperature dependent and not linear. Based on many experiments using the CIROCO test loop, taking into account different temperatures, mass transfers and chemicals, (16) has been simplified as

()

where H(T) is a temperature-dependent function normalized to K and which leads to a hydrogen content (in mg kg⁻¹) equivalent for increasing the iron solubility. Only experiments can lead to this function and data are not shown.

The Sanchez Calder model [77] was developed to predict the rate of FAC in steam extraction lines. It incorporated most of the processes shown in Figure 26, with an equation similar to the EDF model, and highlighted their view of the importance of the oxide porosity, which was subsequently incorporated into some other models.

Workers at Penn state Uni [79] pointed out the basic Sanchez Calder model predicted rates that were 100 to 1000 times smaller than measured rates and suggested changes to the model including:

(i)
improved magnetite solubility data,
(ii)
assumption that porosity was a function of oxygen content of water,
(iii)
introduction of several piping configurations and surface finishes.

Since the occurrence of FAC at the outlet headers in the carbon steel primary circuit of CANDU reactors and the failure of a condensate pipe downstream of an orifice at Mihama PWR, various other mechanistic approaches have been formulated.

Burrill and Cheluget [80] followed a similar approach to CEGB workers in having the magnetite solubility (calculated using S&B) as a function of potential and thus the corrosion rate. However under CANDU condition of high pH and high temperature the dependency of magnetite solubility could be less than the normally accepted [H]^1/3 relationship.

Canadian/Japanese Approach [4, 15, 32, 81, 82]. Lister and Long suggested that an earlier model [83] which incorporated both film dissolution and mass transfer could not explain the occurrence of FAC on CANDU outlet feeders. This was because the film dissolution step was not sufficiently fast to keep up with the observed FAC rates. In addition because the FAC rate was a function of the velocity to a power of 1.5–2 it was stated that the surface shear stress (τ) must be important in causing magnetite removal. The stages in this model are thus as follows.

(1)
Some magnetite dissolution occurs.
(2)
Dissolution loosens magnetite crystals.
(3)
Surface shear stress spalls or erodes crystals.
(4)
Thinned magnetite is less protective.

An electrochemical model was developed which could predict corrosion potentials magnetite solubility’s and FAC rates.

Subsequent work in collaboration with Japanese workers, including Uchida, has subsequently developed their own evaluation program because Unfortunately, details of their (other models) theoretical basis and of the data bases of the program packages are classified due to intellectual property rights. Both traceability of the computer program package and its validation are required for making policy on plant reliability when applying the package calculations.

A paper covering the evaluation of FAC simulation code based on verification and validation has been published [82], which describes the steps involved as follows.

Step 1. Define flow velocities and temperatures in system: 1D CFD code RELAPS used.

Step 2. Calculate O₂ levels ECP, and so forth: 1D O₂-hydrazine reaction code CORRENV used.

Step 3. Distribution of mass transfer coefficients: 3D CFD code PLASY MTCEXTRA used.

Step 4. Danger zone evaluation: chart analysis DRAWTHREE-FAC.

Step 5. Distribution of wall thinning: wall thinning code WATH.

Step 6. Evaluation of residual life and effect of counter measures: final evaluation DRAWTHREE-FAC.

Interestingly this paper appears to indicate the importance of obtaining the mass transfer rate but does not mention the importance of the surface shear stress.

5.3. Empirical Models

The Keller model [84–86] was probably one of the first predictive models. The basis for the formulation was a combination of experience gained from damage in wet steam systems and the pressure drops expected at various components:

()

where K_c is a component geometry factor and Ks is a constant that must be exceeded for FAC to occur, X is the steam quality, T is the temperature, and V is the velocity.

This was clearly inadequate since no environmental influence was included and was subsequently modified by Kastner et al. [85] to include the following.

(a)
Environmental factors.
(b)
A modified K_c, which also included downstream influences:
()

After the Surry failure this was developed into WATHEC and is used in conjunction with DASY to manage data obtained from NDT examination.

EPRI CHEC [2, 87, 88] (Chexal and Horriwtz). After the Surry failure EPRI collected all British, French, and German experimental data together with USA plant data. Other than being consistent with mechanistic understanding no presumptions were made as to the form of the correlation between FAC rate and all the influencing variables resulting in the formulation:

()

where α is a factor for void fraction in two-phase flow. There have been various modifications and improvements made to this code and its use in plant examination.

5.4. Other Models

A trained artificial neural network (ANN) was used [79] to make predictions, but the details of the results were only given in graphical form. The following was suggested.

The combination of a deterministic model which reflects a mechanistic picture of FAC and a purely nondeterministic ANN model which reflects best experimental representation of the phenomenon are the best tools for extracting information from complex phenomenon such as FAC [79].

A Russian program ECW-02 based on CHECWORKS has been developed, and a Ukrainian program KASESC based on WATHEC has also been produced. RAMEK is a more original Russian approach that has been described and reviewed [8] that appears to combine a loss rate due to mass transfer with a loss rate due to the surface shear stress peeling of the oxide layer.

Various models [89–91] have been developed to predict droplet attack at bends in two-phase flow, but they appear to ascribe damage to be mechanical in nature. As outlined earlier the conditions causing such attack, as opposed to corrosion, need defining.

The relative usage of the various programs is that CHECWORKS is used in USA, Canada, Taiwan, Japan, South Korea, Czechia, Slovakia, and Slovenia ~153 units, EDF is only used in France but in all 58 units, and COMSY is used in Germany, Spain, Finland, Hungary, and Bulgaria ~17 units.

6. Discussion

A simplified summary of how the prediction schemes deal with some of the variables that have been dealt with in this review is given in Table 5, and suggested reasons for the bell shaped dependency of FAC rate with temperature are summarized in Figure 29.

Table 5. Models and how they deal with key variables.

Model	FAC function of V^m or Kⁿ	Roughness effects	Solubility relationship	Cause of FAC reduction at Low T and High T
CEGB [54, 66, 67, 70, 71]	Nonlinear n > 1 < 3.	Acknowledged but not specifically integrated.	S and B	MDR * Solubility

EdeF [65, 69, 72–76]	Linear n = 1 or less	Yes and specified relationship	S and B	Porosity Porosity MDR

Sanchez Calder [77]	Linear n = 1 or less	Apparently not	S and B	Porosity Porosity MDR

Penn S [79]	Mechanistic model-linear? ANN model nonlinear.	Yes but not specified	Their own which is bell shaped at pH 7 and increases with temperature at pH 9	Unclear

EPRI [2, 87, 88]	Not stated but m apparently between 0.6 and 0.7	Yes but suggested and did not occur	Unclear which or if incorporated into model, though clearly identified differences between S and B and T and LeB data	MDR Solubility

Siemens KWU [84–86]	FAC_rate e^cV where c is complex f of time and temperature	Apparently not	Unclear which or if incorporated into model	Unclear

Lister and Lang [15] and Uchida et al [81]	Nonlinear n > 1 due to shear stress on oxide	Yes	S and B or T and LeB?	Unclear

^*MDR is magnetite dissolution reaction.

6.1. Importance of Mass Transfer

It is widely agreed that the mass transfer coefficient is the hydrodynamic parameter that controls the occurrence and rate of FAC. A relationship between rate of FAC and the mass transfer coefficient, with a power dependency of greater than one, is an erroneous reason to invoke the importance of τ the surface shear stress. It is believed that there are more cogent reasons to reject the involvement τ as an important parameter. These have been dealt with in detail earlier and elsewhere. Briefly the variations in τ, K, turbulence level, and flow assisted corrosion rate with distance downstream of an orifice are sufficient to confirm that τ is not important. It is probable that a similar statement will be found for other regions where detached flow occurs and the relationship between mass transfer heat-transfer and pressure drop breaks down.

6.2. Relationship between FAC and Mass Transfer and Magnetite Solubility

It is clear that there is not always a simple linear relationship between the FAC rate and the mass transfer rate, for example, the variation in FAC downstream of an orifice. Of the various predictive schemes only the EdF model appears to suggest a linear model, and the position of the EPRI code is unclear. Figure 28 compares some CEGB and EDF data.

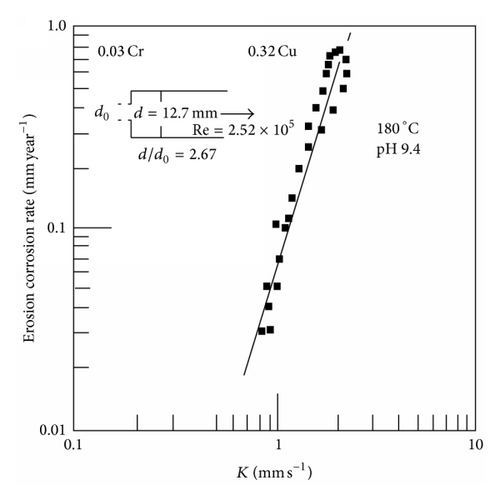
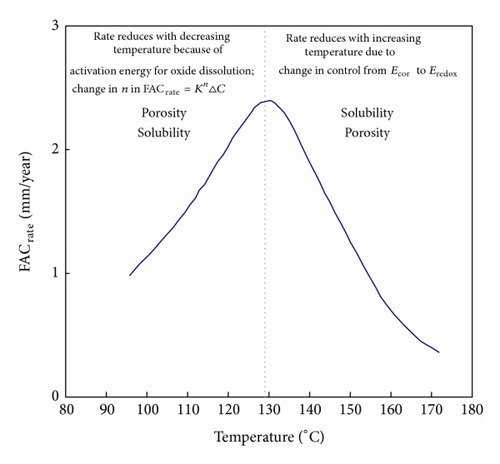
It has been suggested that at low temperatures the FAC rate is limited by the magnetite dissolution rate. However an empirical fit of the data produced an activation energy that was a function of the mass transfer rate [70]. At temperatures above the FAC peak it has been suggested that redox reactions could become more important than the corrosion potential in determining the rate of FAC. Both of these situations would produce a lower dependency on mass transfer than at the peak temperature where the highest value of n is associated with the maximum feedback between the FAC rate, the corrosion potential, the production of hydrogen, and the solubility of magnetite.

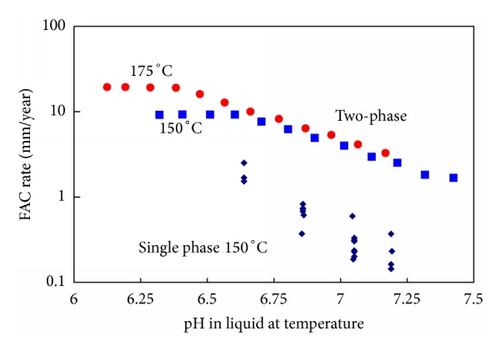
Except for very high plateau FAC rates at low pH’s (Figure 30) there is no convincing evidence for the importance of any processes other than mass transfer and magnetite solubility. The importance of magnetite dissolution kinetics being limiting at low temperatures appears to result from the widespread use of the solubility data of Sweaton and Baes. Most importantly this data suggests that magnetite solubility increases with decreasing temperatures down to about 60°C. However the data of Tremaine and LeBlanc show a bell shaped magnetite solubility curve (Figure 19), which more closely resembles the temperature dependence of FAC. In addition there are theoretical reasons why solubility should not be related to hydrogen partial pressure at low temperatures. Other reasons proposed to explain the temperature dependence of the FAC rate are summarized in Figure 28.

6.3. Influence of Roughness Development

The way the different models deal with roughness development, mass transfer, and the influences on the rate of FAC is summarised in Table 5. It appears that only the WATHEC model does not incorporate roughness effects. However it is not clear how the smooth to rough surface transition is handled by any of the models. The EdF model incorporates a formulation very similar to Figure 12 with the factor 0.01 being replaced with 0.193(ε/d) ^0.2. This would appear a reasonable formulation in line with pressure drop formulations. However it is clear that that as Re increases the size of scallops produced by FAC decreases, although the mass transfer enhancement over a smooth surface is increased; this appears inconsistent, except possibly during the initial stages of attack.

6.4. Mechanistic Comments on Prediction Models

It is surprising that after over 40 years of investigation and development there is no widespread agreement on a number of important mechanistic aspects, which have an impact on the ability to predict the rate of FAC, these include the following.

(1)
The relevance of various processes particularly oxide porosity.
(2)
The relationship between FAC and K.
(3)
Which solubility data to use.
(4)
The mechanism of improvement due to Cr content of the steel.
(5)
The importance and treatment of roughness development.

Thus despite the ability to prevent its occurrence to say that FAC is well understood is somewhat premature.

6.5. Relationship of FAC to Deposition and SCC?

The roughness that develops during both FAC and the deposition of rippled magnetite both increase the resistance to flow. Such effects are usually represented graphically in terms of the friction factor (f) as a function of the Reynolds number; the friction factor relates the pressure drop and thus τ to the velocity. Such a diagram was constructed, by Moody for pipes having roughness elements of varying heights and distributions. Similar diagrams can be constructed for surfaces with uniform roughness, for example, with sand grains. There are some differences between these two types of diagrams [18]. However in both cases under turbulent conditions the friction factor increases with the relative roughness (ε/d) and decreases with increases in Reynolds number. A simplified equation was recommended [18] to estimate such effects:

()

For surfaces that roughen as a result of dissolution or deposition the relative roughness produced decreases with increasing flow or Re. The evidence is that such roughness produced a greater resistance than expected from its ε/d value. From the upper bound mass transfer correlation and the analogy with heat and momentum transfer a single upper bound value of f can be estimated as a function of Re as f = 0.02Re, but this has not been tested. It has been suggested, and there is some evidence for, the resistance peaking at the Reynolds number at which the roughness was formed [50, 92].

The difficulties predicting the occurrence of deposition have been indicated [64], although a velocity below 1.6–2.9 m/s was stated [93] as necessary to prevent the occurrence in straight tubes; otherwise pressure drop increases of 20 times at a Re of 10⁶ could occur. Deposition appears preferentially at regions of high mass transfer and it has been suggested [94] that this is due to electrokinetically generated currents at regions of separated flow, but deposition does occur on straight pipes and bends, Figure 31. If electrokinetically currents are important deposition might be expected to occur at any dissolved iron levels (like electrodeposition). However there is still some debate about the roles of soluble or particulate iron. Like FAC deposition can be controlled by the addition of oxygen to the water or pH changes reducing the iron solubility.

The SCC of highly stressed experimental orifice holders undergoing FAC was reported [12]. It was suggested that the electrochemical conditions for FAC and SCC are often similar. For example it was shown that the potential range promoting SCC and FAC, of carbon steels in carbonate solution, is identical. Also both SCC and FAC of carbon steels occur in carbonate, nitrate, and caustic solutions. The relationship between oxide solubility and crack propagation has also been suggested [95]. However from a practical viewpoint for carbon steels in water it is clear that cracking is favored by oxidizing conditions, which inhibit the occurrence of FAC. The occurrence of both FAC and SCC assumed importance by the occurrence of both FAC and SCC on the outlet headers of a CANDU plant; as yet there does not seem to be a full understanding of such cracking.

7. Preventing the Occurrence of FAC

If the three major influences on FAC are considered, that is, material, environmental, and hydrodrodynamic, as shown in Figure 2, then how to prevent its occurrence is straightforward and depends if at the design stage or postconstruction and into operation.

The history of the British AGRs once through steam generators illustrates this rather well. Damage was first observed at and downstream of the flow control orifice assemblies situated in the feedwater inlet headers. These are accessible and the problem was corrected by a redesign which included a stainless steel section of tubing downstream of the orifice. However this problem highlighted the risk to the carbon steel bends in the economizer section of the boiler, which was controlled initially by raising the pH. Although this appeared successful it limited the life of ion exchange beds. It was known that oxygen additions to the feedwater could be beneficial in terms of general corrosion [96, 97]. A large program demonstrated that adding a small amount of oxygen prevented FAC [78, 98]. High resolution surface activation measurements of FAC rate confirm this as shown in Figure 32. In addition it was shown that additions of oxygen and hydrazine could be made together and that the oxygen would inhibit FAC in the economizer prior to being reduced by the hydrazine and thus minimise the possibility of SCC at oxidising potentials. Thus very cleverly two additions can be made to the secondary water, having opposite effects and preventing two forms of corrosion occurring in different regions of the boiler.

It was postulated that the amount of oxygen that was needed to be added to prevent FAC was related to the FAC rate by Faradic equivalence:

()

where P is a constant as defined in Figure 33. Note that the concentration (weight/volume) of oxygen is given by O₂ ppm × ρ_water. The slope of the line in Figure 33 is a function of five parameters and its value seems to be an unreliable way of obtaining mechanistic information about the reactions involved.

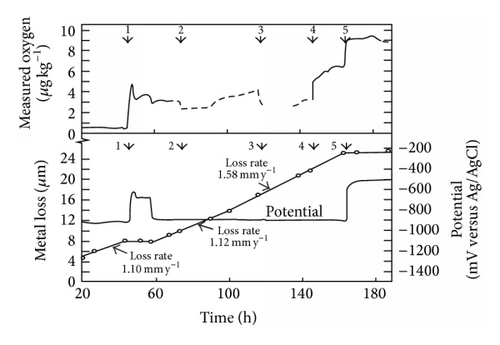
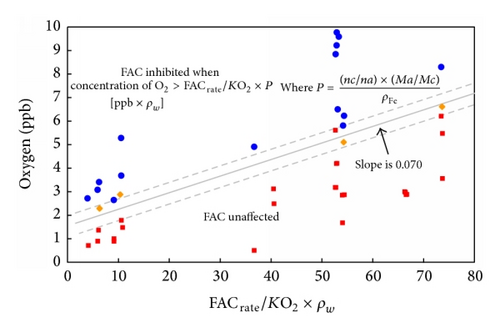
The success of such oxygen additions has been described [99] and the approach has been adopted in other situations [100]. Later AGR boilers were constructed using a 1%Cr 0.5%Mo steel after extensive testing had confirmed its suitability. The use of 1%Cr 0.5%Mo steel has the advantage that no postweld heat-treatment is usually required unlike 2.25%Cr 1%Mo and higher alloyed steels.

8. Conclusions

(1)
The available evidence continues to support the use of the mass transfer coefficient (K) as the best hydrodynamic parameter to characterize FAC in power plant.
(2)
The fundamental relationship between K and the rate of flow accelerated corrosion continues to be a significant difference between the different predictive schemes. However, there is strong evidence that the rate of FAC is not always a simple linear function of the mass transfer rate.
(3)
With normal flow as roughness develops mass transfer increases and the rate of FAC increases. There is now more evidence that this is much less important with detached flow.
(4)
It is clear that the influence of the environmental parameters such as temperature, pH, and oxygen content is through their effect on the solubility of magnetite. However, the details of this and the variation of magnetite solubility deserve closer attention. In particular it might prove possible to explain the temperature dependency of FAC in terms of magnetite solubility and its relationship to hydrogen partial pressure, without having to invoke a change in the rate controlling step.
(5)
There is the possibility that at higher pH’s and temperatures, for instance those in the CANDU primary system the effect of hydrogen partial pressure, on magnetite solubility might not be proportional to . As pH increases, at high temperatures, there will be a gradual reversal in the effect of hydrogen content on solubility, from being proportional to to .
(6)
The beneficial effect of chromium continues to be demonstrated under all conditions. However, it is not clear if this effect is due to a reduction in the solubility of the magnetite, a change in the kinetics of oxide dissolution or its influence on the oxide porosity.
(7)
It is clear that oxygen additions can prevent FAC but such additions to the environment might lead to other problems.
(8)
There is still no agreement on a number of important mechanistic aspects. The mechanistic models appear to have adjustable parameters particularly the f(T) in the EDF code and the n in the Kⁿ dependency of the FAC rate, in the CEGB model.
(9)
The pragmatic models do not give enough information to completely understand their operation.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

References

1 P. H. Berge and F. Khan, Proceedings of the Conference on Corrosion-Erosion of Steels in High Temperature Water and Wet Steam, 1983, Paris, France, Electricite de France.
Google Scholar
2 Flow-accelerated corrosion in power plants, TR-106611, 1996, EPRI.
Google Scholar
3 Bignold G. J., de Whalley C. H., Garbett K., Garnsey R., Woosey I. S., Libaert D. F., and Sale R., Erosion-corrosion of mild steel ammoniated water, Proceedings of the 8th International Congress on Metallic Corrosion, 1981, Mainz, Germany, 1548–1554.
Google Scholar
4 Uchida S., Evaluation method for FAC of components by corrosion analysis coupled with flow dynamics analysis, Proceedings of the Annual Meeting of the Executive Committee and Working Groups of the International Association for the Properties of Water and Steam (IAPWS ′06), September 2006, Witney, UK.
Google Scholar
5 Poulson B., S Greenwell B., Chexal B., and Horowitz G., Modelling hydrodynamic parameters to predict flow assisted corrosion—water reactors, Proceedings of the 5th International Conference on Environmental Degradation of Materials in Nuclear Power Systems, 1992, La Grange Park, Ill, USA, American Nuclear Society.
Google Scholar
6 Slade J. P. and Gendron S. T., T. R. King, P. J. King, and L. Nelson, FAC and cracking of carbon steel piping in primary water-operating experience at the Point Lepreau Generating station, Proceedings of the 12th International Conference on Envirinmental Degradation of Materials in Nuclear Power Systems-water Reactors, 2005, 773–784.
Google Scholar
7 Cragnolina G., G. J. Theus and J. R. Weeks, A review of erosion-corrosion of steels in high temperature water, Proceedings of the 3rd Environmental Degradation of Materials in Nuclear Power Systems—Water Reactors, 1988, The Metallurgical Society, 397–406.
Google Scholar
8 Betova I., Bojinov M., and Saario, Predictive modeling of flow-accelerated corrosion-unresolved problems and issues, VTT research report No VTT-R-08125-10, 2010.
Google Scholar
9 Garud Y. S., Issues and advances in the assessment of flow accelerated corrosion, Proceedings of the 14th International Conference on Environmental Degradation. (2008) .
Google Scholar
10 Bignold G. J., Erosion-corrosion: history causes and remedies, Modern Power Systems. (2005) 25, no. 2, 11–15.
Google Scholar
11 Poulson B., Electrochemical measurements in flowing solutions, Corrosion Science. (1983) 23, no. 4, 391–430, https://doi.org/10.1016/0010-938X(83)90070-7, 2-s2.0-0020506888.
Google Scholar
12 Poulson B., J. E. Strutt and J. R. Nichols, Predicting the occurrence of erosion corrosion, Plant Corrosion: Prediction of Materials Performance, 1987, Ellis Harwood, Chichester, UK, 101–132.
Google Scholar
13 Poulson B., Advances in understanding hydrodynamic effects on corrosion, Corrosion Science. (1993) 35, no. 1–4, 655–661, https://doi.org/10.1016/0010-938X(93)90201-Q, 2-s2.0-0027832556.
Google Scholar
14 Poulson B., L. L. Shrier, R. A. Jarman, and G. T. Burnstein, Erosion-Corrosion, Corrosion, 1994, 3rd edition, no. chapter 1–11, Butterworth/Heinnmann, Oxford, UK.
Google Scholar
15 Lister D. H. and Lang L. C., A mechanistic model for predicting FA and GC of carbon steel in reactor primary coolants, Proceedings of the International Conference on Water Chemistry of Nuclear Reactor Systems (CHIMIE ′02), 2002, Avignon, France, Societe Francaise d′Energie Nucleaire.
Google Scholar
16 Silverman D. C., K. J. Kennelley, R. H. Hausler, and D. C. Silverman, RCE-an approach for predicting velocity sensitive corrosion, Flow Induced Corrosion: Fundamental Studies and Industrial Experience, 1992, NACE, Houston, Tex, USA.
Google Scholar
17 Hewitt G. F., Measurement of two phase flow parameters, 1978, Academic Press, London, UK.
Google Scholar
18 Massey B., Mechanics of Fluids, 2006, 8th edition, Taylor & Francis, London, UK, Revised by J. Ward-Smith.
Google Scholar
19 Wragg A. A., Applications of the limiting diffusion current technique in chemical engineering, Chemical Engineer. (1977) no. 316, 39–49, 2-s2.0-0017428260.
Google Scholar
20 Mizushina T., The electrochemical method in transport phenomena, Advances in Heat Transfer. (1971) 7, 87–161.
Google Scholar
21 Poulson B. and Robinson R., The use of a corrosion process to obtain mass transfer data, Corrosion Science. (1986) 26, no. 4, 265–280, https://doi.org/10.1016/0010-938X(86)90048-X, 2-s2.0-0022562287.
Google Scholar
22 Coney M. W. E., Wilkin S. J., and Oates H. S., Thermal-hydraulic effects on mass transfer behaviour and on erosion corrosion metal loss rate paper 13 in ref 1, 1983.
Google Scholar
23 Wang D. D., Characterization of local mass transfer rate downstream of an orifice, Open Access Dissertations and Theses. Paper 7142, 2012, http://digitalcommons.mcmaster.ca/opendissertations/7142.
Google Scholar
24 Etebari A., Recent innovations in wall shear stress sensor technologies, Recent Patents on Mechanical Engineering. (2008) 1, no. 1, 22–28.
Google Scholar
25 Chouikhi S. M., Patrick M. A., and Wragg A. A., Two phase turbulent wall transfer processes downstream of abrupt enlargements of pipe diameter, Proceedings of the International Conference on the Physical Modelling of Multi-Phase Flow Coventry, 1983, Cranfield, UK, BHRA.
Google Scholar
26 Schmitt G., Werner C., and Bakalli M., Fluid mechanical interactions of turbulent flowing liquids with the wall-revisted with a new electrochemical tool, Paper, 2005, no. 5344, NACE, Houston, Tex, USA.
Google Scholar
27 Schmitt G. and Bakalli M., Maximum flow intensities at tools for measuring flow influenced corrosion, Paper, 2009, no. 9472, NACE, Houston, Tex, USA.
Google Scholar
28 Schmitt G. and Bakalli M., A critical review of measuring techniques for corrosion rates under flow conditions, PowerPlant Chemistry. (2007) 9, no. 6, 89–106.
Google Scholar
29 Nesic S. and Postlethwaite J., Hydrodynamics of disturbed flow and erosion-corrosion part I: single-phase flow study, The Canadian Journal of Chemical Engineering. (1991) 69, no. 3, 698–702, https://doi.org/10.1002/cjce.5450690311, 2-s2.0-0026174053.
Google Scholar
30 Schmitt G. and Gudde T., Local mass transport coefficients and local wall shear stresses at flow disturbances, paper 102 at Corrosion, NACE, Houston, Tex, USA, 1995.
Google Scholar
31 Woolsey I. S., Private communication, 1983.
Google Scholar
32 Lister D. H. and Uchicia S., Reflections on FAC mechanisms, Power Plant Chemistry. (2010) 12, no. 10, 590–597.
Google Scholar
33 Matsumura M. and Oka Y., Mechanism of erosion corrosion of copper alloys, Proceedings of the Pacific Corrosion, 1987, Melbourne, Australia.
Google Scholar
34 Matsumura M., Oka Y., Okumoto S., and Furuya H., Jet-in-slit test for studying erosion corrosion, STP866, 1985, ASTM, https://doi.org/10.1520/STP33791S.
Google Scholar
35 Coney M., CERL Report RD/L/N197/80, 1980.
Google Scholar
36 Schmitt G. and Mueller M., Critical Wall Shear Stresses in CO2 Corrosion of Carbon Steel, 1999, NACE, Houston, Tex, USA, Paper 44 Corrosion 99.
Google Scholar
37 Poulson B. and Robinson R., The local enhancement of mass transfer at 180° bends, International Journal of Heat and Mass Transfer. (1988) 31, no. 6, 1289–1297, https://doi.org/10.1016/0017-9310(88)90071-3, 2-s2.0-0024031720.
Google Scholar
38 Poulson B., Mass transfer from rough surfaces, Corrosion Science. (1990) 30, no. 6-7, 743–746, https://doi.org/10.1016/0010-938X(90)90037-6, 2-s2.0-0025068164.
Google Scholar
39 Poulson B., Measuring and modelling mass transfer at bends in annular two phase flow, Chemical Engineering Science. (1991) 46, no. 4, 1069–1082, https://doi.org/10.1016/0009-2509(91)85100-C, 2-s2.0-0025790699.
Google Scholar
40 Poulson B., Greenwell B. S., Chexal B., and Horowitz G., B. Dooly and A. Bursik, Roughness effects on flow assisted corrosion, Proceedings of the International Conference on Interaction of Iron Based Materials with Water and Steam, 1993, EPRI Palo Alto EPRI TR 102102.
Google Scholar
41 Poulson B., Complexities in predicting erosion corrosion, Wear. (1999) 233–235, 497–504, https://doi.org/10.1016/S0043-1648(99)00235-5, 2-s2.0-17544402999.
Google Scholar
42 Uchida S., Naitoh M., Uehara Y., Okada H., and Lister D. H., Evaluation method for FAC of components by corrosion analysis coupled with flow dynamics analysis, Proceedings of the 13th International Conference on Environmental Degradation of Materials in Nuclear Power Systems, August 2007, Whistler, Canada, CNS.
Google Scholar
43 Hoashi E., Yoshihashi-Suzuki S., Kanemura T. et al., Development of 3D CFD technology for flow-assisted corrosion, Proceedings of the Conference on Water Chemistry of Nuclear. Reactor Systems (NPC ′08), 2008, Berlin, Germany.
Google Scholar
44 Pietralik J. M. and Smith B. A. W., CFD application to FAC in feeder bends, Proceedings of the 14th International Conference on Nuclear Energy (ICONE ′06), 2006, Miami, Fla, USA.
Google Scholar
45 Pietralik J. M. and Schefski C. S., Flow and mass transfer in bends under FAC wall thinning conditions, Proceedings of the 17th International Conference on Nuclear Energy (ICONE ′09), 2009, Brussels, Belgium.
Google Scholar
46 Zinemams D. and Herszaz A., Flow accelerated corrosion: flow field and mass transport in bifurcations and nozzles, Proceedings of the International Conference on Water Chemistry for Nuclear Reactor Systems, 2008, Berlin, Germany, NPC.
Google Scholar
47 Yoneda K., Evaluation of hydraulic factors affecting flow accelerated corrosion and its verification with power plant data, Proceedings of the ASME 2009 Pressure Vessels and Piping Conference, 2009, Prague, Czech Republic, PVP.
Google Scholar
48 Allen J. R. L., Bed forms due to mass transfer in turbulent flows: a kaleidoscope of phenomena, Journal of Fluid Mechanics. (1971) 49, 49–63.
Google Scholar
49 Blumberg P. N. and Curl R. L., Experimental and theoretical studies of dissolution roughness, Journal of Fluid Mechanics. (1974) 65, no. 4, 735–751, https://doi.org/10.1017/S0022112074001625, 2-s2.0-0016383196.
Google Scholar
50 Thomas R. M., Size of scallops and ripples formed by flowing water, Nature. (1979) 277, no. 5694, 281–283, https://doi.org/10.1038/277281a0, 2-s2.0-0008478925.
Google Scholar
51 Tomlinson L. and Ashmore C. B., Erosion corrosion of carbon and low alloy steels by water at 300 degree C, The British Corrosion Journal. (1987) 22, no. 1, 45–52, https://doi.org/10.1179/000705987798271839, 2-s2.0-0023093076.
Google Scholar
52 Crockett H. M. and Horowitz J. S., Low temperature FAC, Proceedings of the ASME PV&P Div (PVP ′09), 2009, Prague Czech Republic, ASME.
Google Scholar
53 Tremaine P. R. and LeBlanc J. C., The solubility of magnetite and the hydrolysis and oxidation of ferrous ions in water to 300°C, Journal of Solution Chemistry. (1980) 9, no. 6, 415–441.
Google Scholar
54 Bignold G. J., B. Dooly and A. Bursik, Erosion-corrosion of steels in feedwater—a broader application of the theory, Proceedings of the International Conference on Interaction of Iron Based Materials with Water and Steam, 1993, Palo Alto, Calif, USA, EPRI, EPRI TR 102102.
Google Scholar
55 Ziemniak S. E., Jones M. E., and Combs K. E. S., Magnetite solubility and phase stability in alkaline media at elevated temperatures, Journal of Solution Chemistry. (1995) 24, no. 9, 837–877, https://doi.org/10.1007/BF00973442, 2-s2.0-21844494176.
Google Scholar
56 Sweeton F. H. and BaesC. F.Jr., The solubility of magnetite and hydrolysis of ferrous ion in aqueous solutions at elevated temperatures, The Journal of Chemical Thermodynamics. (1970) 2, no. 4, 479–500, https://doi.org/10.1016/0021-9614(70)90098-4, 2-s2.0-0000294085.
Google Scholar
57 Bohnsach G., Solubility of Magnetite in Water and Aqueous Solutions of Acid and Alkalies, 1987, Vulkan, Essen, Germany.
Google Scholar
58 Walker S. M. and Thorton E. W., Reanalysis of oxide solubility data, 5, Proceedings of the Water Chemistry of NRS, 1989, London, UK, BNES, 89–95.
Google Scholar
59 Bojinov M., Kinnunen P., Lundgren K., and Wikmark G., Characterisation and modelling of oxide films on stainless steels and Ni alloys in light water reactors, VTT Report No., 2004, no. BTU073-041285.
Google Scholar
60 Bignold G. J., Distribution of solutes between water and steam- influence on two phase, Proceedings of the FAC 8th International Conference Combined Cycle Plants with Heat Recovery Systems, 2006, EPRI Calgary.
Google Scholar
61 Coney M., Erosion-Corrosion: the calculation of mass-transfer coefficients, CERL Report, 1980, no. RD/L/N197/80.
Google Scholar
62 Newman J., R. W. Staehle, B. F. Brown, and J. Kruger, Mass transport and potential distributions in geometries of localized corrosion, 3, Proceedings of the U. R. Evans Conference on Localized Corrosion, 1974, Houston, Tex, USA, NACE, 45–61.
Google Scholar
63 Huijbregts W. M. M., P. H. Berge and F. Khan, The influence of chemical compositionof carbon steel on erosion corrosion in wet steam, Proceedings of the Conference on Corrosion-Erosion of Steels in High Temperature Water and Wet Steam, 1983, Paris, France, Electricite de France.
Google Scholar
64 Poulson B., Gartside H., and Robinson R., P. H. Berge and F. Khan, Corrosion aspects associated with orifice plates and orifice assemblies′, Proceedings of the Conference on Corrosion-Erosion of Steels in High Temperature Water and Wet Steam, 1983, Paris, France, Electricite de France, paper no 10.
Google Scholar
65 Trevin S., FAC in Nuclear Power Plant Components in Nuclear Corrosion Science and Engineering, 2012, Damien Féron Woodhead Publishing, Cambridge, UK.
Google Scholar
66 Bignold G. J., Garbett K., Garnsey R., and Woosey I. S., Erosion-corrosion in nuclear steam generators, INIS Collection Search. (1981) 1–14.
Google Scholar
67 Bignold J. G., DeWhalley C. H., Garbett K., and Woolsey I., Mechanistic aspects of erosion corrosion under boiler feedwater conditions, Water Chemistry, 1983, 3, British Nuclear Energy Society, London, UK, 219–226.
Google Scholar
68 Burrill K. A., Cheluget E. L., and Chocron M., Modelling the effect of Cr on FAC in reactor circuits, Proceedings of the Water Chemistry of NRS BNES, 1999, Bournemouth, UK, 528–537.
Google Scholar
69 Bouchacourt M., Improvements in EC mechanistic model: role of surface film, Water Chemistry of Nuclear Reactor Systems, 1992, 6, BNES, London, UK, 338–340.
Google Scholar
70 Bignold G. J., Garbett K., and Woolsey I. S., Erosion corrosion in boiler feedwater; comparison of laboratory and plant data, Proceedings of the UK Corrosion Conference, 1983, Birmingham, UK, Institute of Corrosion Science and Technology.
Google Scholar
71 Bates A. J., Bignold G. J., Garbett K., Middleton W. R., Penfold D., Tittle K., and Woolsey I. S., CEGB single phase erosion-corrosion research programme, Nuclear Energy. (1986) 25, no. 6, 361–370, 2-s2.0-0022990656.
Google Scholar
72 Ducreux B. J. and Saint-Paul P., Effects of chemistry on erosion-corrosion of steels in water, Proceedings of the Water Chemistry of NRS 2 BNES, London, UK, 19–23.
Google Scholar
73 Ducreux J., The influence of flow velocity on the corrosion-erosion of carbon steel in pressurized water, Proceedings of Water Chemistry of Nuclear Reactor Systems, London, UK, British Nuclear Energy Society, 227–233.
Google Scholar
74 Bouchacourt M. and Remy F.-N., EDF Study of FAC for the French PWR Secondary Circuit, 1991, NACE, Cambridge, UK, Predicting the life of Corroding Structures.
Google Scholar
75 Pavageau E.-M., de Bouvier O., Trévin S., Bretelle J.-L., and Dejoux L., Dejoux Update of the water chemistry effect on the FAC rate of carbon steel: iinfluence of hydrazine, boric acid, ammonia, morphine and ethanolamine, Proceedings 13th International Conference on Environmental Degradation of Materials in Nuclear Power Systems, August 2007, Whistler, Canada, CNS.
Google Scholar
76 Ardillon E., Villain B., and Bouchacourt M., Probabilistic analysis of FAC in French PWR: the probabilistic version of BRT-CICERO version 2.
Google Scholar
77 Sanchez-Caldera L. E., Griffith P., and Rabinowicz E., The mechanism of corrosion-erosion in steam extraction lines of power stations, Journal of Engineering for Gas Turbines and Power. (1988) 110, no. 2, 180–184, https://doi.org/10.1115/1.3240099, 2-s2.0-0023777323.
Google Scholar
78 Woolsey I. S., Bignold G. J., de Whalley C. H., and Garbett K., The influence of oxygen and hydrazine on E-C behaviour and electrochemical potentials of carbon steel under boiler feedwater conditions, Proceedings of the 4th International Conference on Water Chemistry of Nuclear Reactor Systems, 1986, British Nuclear Energy Society.
Google Scholar
79 Urquidi-Macdonald M., Vooris D. V., and Macdonald D. D., Prediction of single phase erossio corrosion in mild steel pipes using artificial neural networks and a deterministic model, Corrosion 95 paper 546 NACE, 1995.
Google Scholar
80 Burrill K. A. and Cheluget E. L., Corrosion of CANDU outlet feeder pipes, Proceedings of the JAIF International Conference on Water Chemistry, 1998, Kashiwazaki, Japan, NPP.
Google Scholar
81 Uchida S., Naito I. M., Uehara Y., Okada H., Koshizuka S., and Lister D. H., Evaluation of Flow Accelerated Corrosion of PWR Secondary Components by Corrosion Analysis Coupled with Flow Dynamics Analysis, 2008, Springer, Berlin, Germany.
Google Scholar
82 Uchida S., Naitoh M., Okada H., Ohira T., Koshizuka S., and Derek H., Lister evaluation of FAC simulation code based on verification and validation, Power Plant Chemistry. (2010) 12, no. 9, 550–559.
Google Scholar
83 Cook W. G., Lister D. H., and McInerney J. M., The effects of high liquid velocity and coolant chemistry on material transport in PWR coolants, Water Chemistry of Nuclear Reactor Systems, 2000, 8, BNES, London, UK.
Google Scholar
84 Keller H., Erosionskorrosion in Nassdampfturbinen, VGB Kraftwerkstechnik. (1974) 54, no. 5, 292–295.
Google Scholar
85 Kastner W., Erve M., Henzel N., and Stellwag B., Calculation code for erosion corrosion induced wall thinning in piping systems, Nuclear Engineering and Design. (1990) 119, no. 2-3, 431–438, https://doi.org/10.1016/0029-5493(90)90182-W, 2-s2.0-44949289844.
Google Scholar
86 Nopper H. and Zanderepri A., Lifetime evaluation of plant components affected by FAC with the COMSY code, Proceedings 13th International Conference on Environmental Degradation of Materials in Nuclear Power Systems, August 2007, Whistler, Canada, CNS.
Google Scholar
87 Schefski C., Pietralik J., Dyke T., and Lewis M., Flow-accelerated corrosion in nuclear power plants: application of checworks at darlington, Proceedings of the 3rd CNS International Conference on CANDU Maintenance, November 1995, Toronto, Canada.
Google Scholar
88 Crockett H. M. and Horowitz J. S., Determining FAC degradation from NDE data, Proceedings of the ASME Pressure Vessels and Piping Conference, July 2009, Prague, Czech Republic, 909–918, 2-s2.0-77953007967.
Google Scholar
89 Ohira T., Motira R., Tanji K. et al., Prediction of liquid droplet impingement erosion (LDI) trend in actual NPP, Proceedings of the AMSE PVP, 2009, Prague, Czech Republic.
Google Scholar
90 Morita R., Inada F., and Yoneda K., Development of evaluation system for liquid droplet impingement erosion (LDI), Proceedings of the AMSE PVP 20009, 2009, Prague, Czech.
Google Scholar
91 Satou M., Sato T., and Hasegawa A., Role of oxide layer on wall thinning caused by liquid droplet impingement (PVP ′09), Proceedings of the AMSE Pressure Vessels and Piping Conference, 2009, Prague, Czech Republic, https://doi.org/10.1115/PVP2009-77685.
Google Scholar
92 Schoch W., Wiehn H., Richter R., and Schuster H., Increase in pressure loss and magnetite formation in a benson boiler, British Corrosion Journal. (1971) 6, 258–268.
Google Scholar
93 Wyatt L. M., Materials of Construction for Steam Power Plant, 1976, Applied Science Publishers, London, UK.
Google Scholar
94 Woolsey M. I., Thomas R. M., Garbett K., and Bignold G. J., Occurrence and prevention of enhanced oxide deposition in boiler flow control orifices, 1, Proceedings of the 5th International Conference on the Water Chemistry of Nuclear Reactor Systems, London, UK, BNES, 219–228.
Google Scholar
95 Weeks J. R., Vyas B., and Isaacs S. H., Environmental factors influencing SCC in boiling water reactors, Corrosion Science. (1985) 25, 757–768.
Google Scholar
96 Freier R. K., Protective film formation on steel by oxygen in neutral water free of dissolved solids, Proceedings of the VGB Feedwater Conference, 1969, 11–17.
Google Scholar
97 Mann G. M. W., The oxidation of Fe base alloys containing less than 12%Cr in high temperature aqueous solutions, High Temperature High Pressure Electrochemistry in Aqueous Solutions: NACE-4, 1976, NACE, Houston, Tex, USA, 34–47.
Google Scholar
98 Gill G. M., Greene J. C., Harrison G. S., Penfold D., and Walker M. A., P. H. Berge and F. Khan, The effects of oxygen and iron in feedwater on erosion-corrosion of mild stel tubing paper 15, Proceedings of the Conference on Corrosion-Erosion of Steels in High Temperature Water and Wet Steam, 1983, Paris, France, Electricite de France.
Google Scholar
99 Quirk G. P., Woolsey I. S., and Rudge A., Use of oxygen dosing to prevent flow-accelerated corrosion in advanced gas-cooled reactors, Power Plant Chemistry. (2011) 13, no. 4.
Google Scholar
100 Ruhle W., Neder H., Holz G., and Schneider V., Oxygen injection into reheater steam of moisture separator reheaters, PowerPlant Chemistry. (2005) 7, no. 6, 355–363.
Google Scholar

Citing Literature

All articles

Predicting and Preventing Flow Accelerated Corrosion in Nuclear Power Plant

Abstract

1. Introduction

2. Hydrodynamics

3. Environmental Variables

4. Material Influences