Discrete Dynamics in Nature and Society
Volume 2014, Issue 1 408972
Research Article
Open Access

Synchronization of Fractional-Order Hyperchaotic Systems via Fractional-Order Controllers

Tianzeng Li, 

Tianzeng Li

School of Science, Sichuan University of Science and Engineering, Zigong 643000, China scu.edu.cn

Sichuan Province University Key Laboratory of Bridge Non-destruction Detecting and Engineering Computing, Zigong 643000, China

Search for more papers by this author
Yu Wang, 

Corresponding Author

Yu Wang

School of Science, Sichuan University of Science and Engineering, Zigong 643000, China scu.edu.cn

Sichuan Province University Key Laboratory of Bridge Non-destruction Detecting and Engineering Computing, Zigong 643000, China

Search for more papers by this author
Yong Yang, 

Yong Yang

School of Science, Sichuan University of Science and Engineering, Zigong 643000, China scu.edu.cn

Search for more papers by this author
First published: 01 April 2014
https://doi.org/10.1155/2014/408972
Citations: 6
Academic Editor: Beatrice Paternoster

Abstract

In this paper, the synchronization of fractional-order chaotic systems is studied and a new fractional-order controller for hyperchaos synchronization is presented based on the Lyapunov stability theory. The proposed synchronized method can be applied to an arbitrary four-dimensional fractional hyperchaotic system. And we give the optimal value of control parameters to achieve synchronization of fractional hyperchaotic system. This approach is universal, simple, and theoretically rigorous. Numerical simulations of several fractional-order hyperchaotic systems demonstrate the universality and the effectiveness of the proposed method.

1. Introduction

Fractional calculus is a 300-year-old mathematical topic. Although it has a long history, it has not been used in physics and engineering for many years. However, during the last twenty years or so, fractional calculus starts to attract increasing attentions of physicists and engineers from an application point of view [1, 2]. It was found that many systems in interdisciplinary fields could be elegantly described with the help of fractional derivatives. Many systems are known to display fractional-order dynamics, such as viscoelastic systems [3], dielectric polarization [4], electrode-electrolyte polarization [5], electromagnetic waves [6], quantitative finance [7], and quantum evolution of complex systems [8].

It is well known that chaos cannot occur in autonomous continuous-time systems of integer-order less than three according to the Poincarè-Bendixon theorem [9, 10]. A famous example of a continuous-time three-order system which exhibits chaos is the Lorenz system [11]. The order of this system can be defined as the sum of the orders of all involved derivatives. However, in autonomous fractional-order systems, it is not the case. For example, it has been shown that the fractional order Chua′s circuit with an appropriate cubic nonlinearity and with order as low as 2.7 can produce a chaotic attractor [12]. In [13], chaos and hyperchaos in fractional-order Rössler equations are discussed, in which it is shown that chaos can exist in the fractional-order Rössler equation with order as low as 2.4, and hyperchaos can also exist in the fractional-order Rössler hyperchaotic system with order as low as 3.8. Also in [14, 15], chaotic behaviors in the fractional-order Chen system are studied and the lowest order to have chaos in this fractional order Chen system is shown to be 2.1 and 2.92, respectively.

In recent years, hyperchaotic system is also considered with quickly increasing interest [16, 17]. Hyperchaotic system is usually defined as a chaotic system with more than one positive Lyapunov exponent, which implies that its dynamics are extended in several different directions simultaneously. It has more complex dynamical behaviors than chaotic system. Typical examples are fractional-order hyperchaotic Chen′s system [18], hyperchaotic Lorenz system [19, 20], and hyperchaotic Rössler system [21–23]. As we known, hyperchaos synchronization is very important, but it is also very difficult. However, there are only a few synchronization methods, such as feedback controller [20, 24] and nonlinear controller [25]. Most of the above synchronization methods concentrate on certain fractional systems, and there are few general methods that can be applied to control arbitrary fractional-order hyperchaotic systems.

On the other hand, the fractional-order control, which is a generalization of the traditional integer-order control, is becoming a matter of concern because of its flexibility and integrity [26–29]. The TID controller [27], the PIλDμ controller [28], and the CRONE controller [29] are the well-known fractional-order controllers. In these papers, it is verified that fractional-order controller is implemented more easily and more efficiently compared to the traditional controller.

Therefore, in this paper, we present a new fractional-order controller to synchronize the arbitrary 4D fractional-order hyperchaotic systems. The control approach which is based on the Lyapunov stability theory has the following three advantages. (1) It is so general that it can be applied to almost all four-dimensional (4D) hyperchaotic systems. (2) It can synchronize the systems very fast with little control cost and no changes on the parameters of the original systems. (3) It is very simple, easily realized experimentally, and more suitable for engineering applications. Numerical simulation results of synchronization of the fractional-order hyperchaotic Chen system, the fractional-order hyperchaotic Lorenz system, and the fractional-order hyperchaotic Lü system demonstrate the effectiveness and the validity of the proposed method.

2. Fractional Derivatives and Fractional Dynamic Systems

The fractional calculus plays an important role in modern science. In this paper, we mainly use the Caputo fractional operators [1, 26]. The Caputo definition of the fractional derivative, which is called smooth fractional derivative, is described as
()
where m is the lowest integer which is not less than q, and Γ is the Gamma function:
()
When we numerically solve the fractional differential equations, we also adopt the improved version of Adams-Bashforth-Moulton algorithm [26, 30] which is proposed based on the predictor-correctors scheme. To explain the method, we consider the following differential equation:
()
The differential equation (3) is equivalent to Volterra integral equation in the following:
()
Now, set h = T/N, tn = nh(n = 0,1, …, N). The integral equation can be discretized as follows:
()
where
()
()
()
The error of this approximation is described as follows:
()
where p = min⁡(2,1 + q).

In this paper, we mainly consider the order 0 < q < 1. There are some general properties of the fractional-order derivative which are described as follows [1, 26].

Property 1. Caputo fractional derivative is a linear operator; that is,

()
where λ, μ are real constants.

Property 2. Caputo fractional derivative satisfies additive index law (semigroup property); that is,

()
holds under some reasonable constraints on the function f(t).

Property 3. For the fractional-order nonlinear system , f(x(t)) satisfies the Lipschiz condition with respect to x; that is,

()
where ∥·∥ is 1-norm and l is a positive constant. Especially, if f(x) = 0 at x = 0. It follows that
()

In the following, we mainly consider a four-dimensional fractional-order nonlinear system:
()
where α(α ∈ (0,1]) is the fractional order of derivatives, x = (x1(t), x2(t), x3(t), x4(t)) T is the system state variable, x(0) = (c1, c2, c3, c4) T is the initial value, and denotes the Caputo fractional-order derivative operator [26]. The equilibrium points of system (14) are calculated via solving f(x*) = 0. Then we have the following conclusion for the stability of these equilibrium points.

Theorem 1 (see [26].)The equilibrium points x* of system (14) are globally asymptotically stable if all the eigenvalues λi  (i = 1,2, …, n) of the Jacobian matrix J = ∂F/∂x, evaluated at x*, satisfy the condition

()

3. Synchronization of the Fractional-Order Hyperchaotic Systems

For the 4D fractional-order nonlinear system (14), we assume that
()
where Ax,y is a bounded matrix with its elements depending on x and y. We consider the system (14) as a drive system, then the response system is given by
()
Adding a control function φ(u) to the system (17), the controlled response system is
()
Let synchronization error e = y − x, the error system from (14) and (18) is obtained as follows:
()
The control function is usually defined as
()
where k is the control parameter matrix which is always diagonal and u is defined as
()
with ω = diag⁡(ω1, ω2, ω3, ω4) being a nonnegative diagonal matrix.

According to the Property 2 and formula (21), we have . In the same way, according to Properties 1 and 3 of the Caputo fractional derivative operator, there is a positive number λ, such that ∥ωe∥ ≤ λ∥u∥. Let ω* be the positive minimum value of {ω1, ω2, ω3, ω4}, then ∥e∥ ≤ λ/ω*∥u∥, and if u = 0, then e = 0.

Then we can easily obtain that the systems (14) and (18) are synchronized if and only if the error system (19) is asymptotically stable at the origin point.

Theorem 2. The fractional-order controller can make the error system (19) asymptotically stable at the origin point; that is, systems (14) and (18) are globally asymptotically synchronized if the control parameters k  (ki ≥ 0,  i = 1,2, 3,4) and ω  (ωi ≥ 0,  i = 1,2, 3,4) satisfy the following conditions:

(1)

()

(2)

()

Proof. Since system (14) is fractional-order hyperchaotic system and Ax,y is a bounded matrix, there is a nonnegative constants M such that ∥Ax,y∥ ≤ M. We introduce a Lyapunov function

()

Differentiating V with respect to t, we have

()
The conclusion would be obtained, if the control parameters k and ω satisfy the following conditions:

(1)

()

(2)

()
After calculation, the above conditions are equivalent to

(1)

()

(2)

()
Hence, we have . Obviously, if and only if u = 0 (or e = 0). Then set is the largest invariant set for the system. According to the LaSalle invariance principle, the fractional-order controller can make the error system (19) be asymptotically stable at origin point, that is, systems (14) and (18) are globally asymptotically synchronized.

Consider a three-dimensional fractional-order nonlinear system

()
where α(α ∈ (0,1]) is the fractional order of derivative, x = (x1(t), x2(t), x3(t)) T is the system state variable, x(0) = (c1, c2, c3) T is the initial value, and denotes the Caputo fractional-order derivative operator. We consider the system (30) as a drive system, then the response system is given by
()
Let synchronization error e = y − x, the error system from (30) and (31) is obtained by the same way:
()
where the control function is usually given as (20). Then we can get the conclusion.

Corollary 3. The fractional-order controller can control the error system (32) responses to the asymptotically stable at the origin point, that is, systems (30) and (31) are globally asymptotically synchronized, if the control parameters k  (ki ≥ 0,  i = 1,2, 3) and ω  (ωi ≥ 0,  i = 1,2, 3) satisfy the following conditions:

(1)

()

(2)

()

4. Simulation and Analysis

In this section, three 4D fractional-order hyperchaotic systems are used as examples to illustrate how to use the results obtained in this paper to analyze the synchronization of fractional-order hyperchaotic systems.

4.1. Synchronization of the Fractional-Order Chen Hyperchaotic System

In 2005, Li et al. [18] proposed a new hyperchaotic chen system form Chen system, which is described as
()
where a, b, c, d, k ∈ ℝ. When a = 35, b = 3, c = 12, d = 7, and 0.085 < r ≤ 0.798, the system (35) is hyperchaotic [18]. Then we consider the fractional version of this system which is given by
()
where α  (0 < α ≤ 1) is the fractional order. When a = 35, b = 3, c = 12, d = 7, and k = 0.5, according to the numerical simulations, the lowest order of this system to generate hyperchaos is 0.946. If we select the order α = 0.96 and initial value (2,2, 1, −1), the system exhibits hyperchaotic behavior, as shown in Figure 1.
Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
Hyperchaotic attractors in the fractional-order hyperchaotic Chen system with α = 0.96. The panels (a) and (b) show the 3D views of x3 − x2 − x1 and x4 − x3 − x2, respectively.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
Hyperchaotic attractors in the fractional-order hyperchaotic Chen system with α = 0.96. The panels (a) and (b) show the 3D views of x3 − x2 − x1 and x4 − x3 − x2, respectively.
We consider the system (36) as a drive system, then the controlled response system is
()
where ki  (i = 1,2, 3,4) is control parameter and . According to systems (36) and (37), the error system is obtained as follows:
()
When the control parameters ki  (i = 1,2, 3,4) and ωi  (i = 1,2, 3,4) satisfy the conditions of Theorem 2, the system (38) can be stabilized to the original point; that is, the synchronization of systems (36) and (37) are achieved.

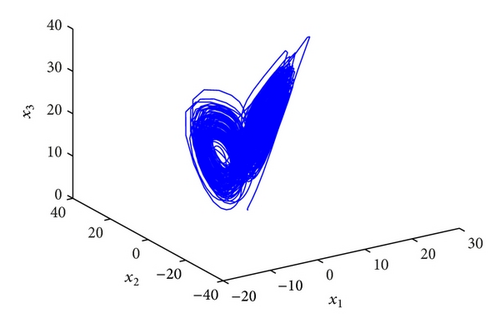
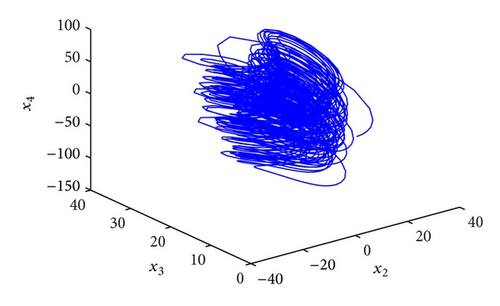
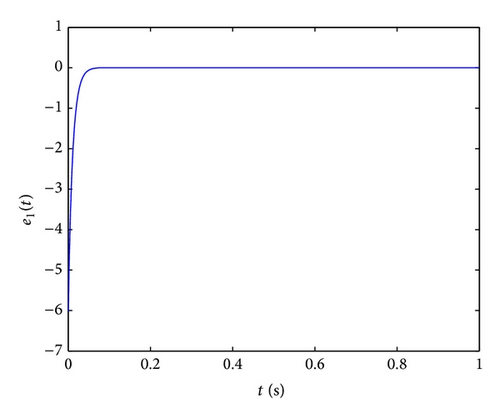
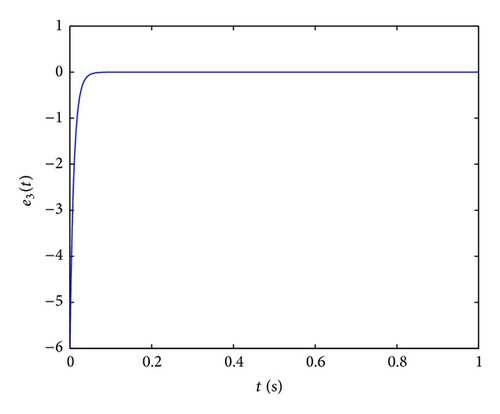
In order to implement this controller easily, we select the parameters k1 = k2 = k3 = k4 = 100, ω1 = ω2 = ω3 = ω4 = 1, and initial values x(0) = (2,2, 1,1), y(0) = (−4, −4, −5, −5), u(0) = 0; the numerical results, illustrated in Figure 2, show that the error system is driven to original point very fast; that is, the system (36) and (37) are synchronized. From Figure 2, we can obtain that two systems are synchronized about at 0.1 s, so the fractional-order controller can synchronize the hyperchaotic Chen systems very effectively.

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Time waveforms of synchronization errors e1 (a), e2 (b), e3 (c), and e4 (d) between two fractional-order hyperchaotic Chen systems.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Time waveforms of synchronization errors e1 (a), e2 (b), e3 (c), and e4 (d) between two fractional-order hyperchaotic Chen systems.
Details are in the caption following the image
Figure 2 (c)
Open in figure viewerPowerPoint
Time waveforms of synchronization errors e1 (a), e2 (b), e3 (c), and e4 (d) between two fractional-order hyperchaotic Chen systems.
Details are in the caption following the image
Figure 2 (d)
Open in figure viewerPowerPoint
Time waveforms of synchronization errors e1 (a), e2 (b), e3 (c), and e4 (d) between two fractional-order hyperchaotic Chen systems.
To get an optimal value of the parameters ki  (i = 1,2, 3,4) which make two hyperchaotic systems synchronize, we continuously increase the parameters k1 = k2 = k3 = k4, form 1 to 4650, in step 1. By the numerical simulations with same initial values, we find the following conclusion.
  • (i)

    When k1 = k2 = k3 = k4 < 5, two systems cannot achieve synchronization.

  • (ii)

    When 5 ≤ k1 = k2 = k3 = k4 < 25, two systems achieve synchronization, but the synchronization times are more than 1 s.

  • (iii)

    When 25 ≤ k1 = k2 = k3 = k4 ≤ 4650, two systems achieve synchronization very fast and the synchronization times are less than 1 s, which are shown in Figure 3(a).

  • (iv)

    When k1 = k2 = k3 = k4 > 4650, two systems cannot achieve synchronization.

Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
The waveform of synchronization time with the control parameters ki  (i = 1,2, 3,4) (a) and time waveforms of synchronization errors between two hyperchaotic Chen systems with parameter ki = 15 (b), 1875 (c), 4500 (d) (i = 1,2, 3,4), respectively.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
The waveform of synchronization time with the control parameters ki  (i = 1,2, 3,4) (a) and time waveforms of synchronization errors between two hyperchaotic Chen systems with parameter ki = 15 (b), 1875 (c), 4500 (d) (i = 1,2, 3,4), respectively.
Details are in the caption following the image
Figure 3 (c)
Open in figure viewerPowerPoint
The waveform of synchronization time with the control parameters ki  (i = 1,2, 3,4) (a) and time waveforms of synchronization errors between two hyperchaotic Chen systems with parameter ki = 15 (b), 1875 (c), 4500 (d) (i = 1,2, 3,4), respectively.
Details are in the caption following the image
Figure 3 (d)
Open in figure viewerPowerPoint
The waveform of synchronization time with the control parameters ki  (i = 1,2, 3,4) (a) and time waveforms of synchronization errors between two hyperchaotic Chen systems with parameter ki = 15 (b), 1875 (c), 4500 (d) (i = 1,2, 3,4), respectively.

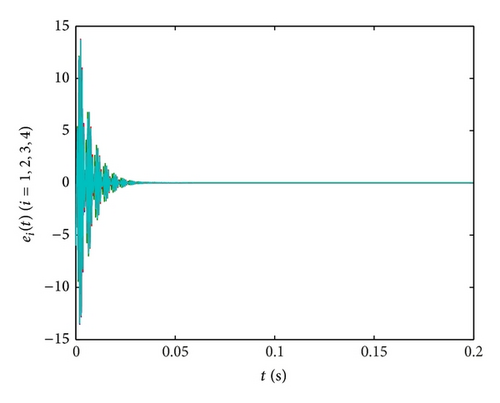
In Figures 3(b)–3(d), the time evolutions of the error functions between systems (36) and (37) are given with ki = 15,1875,4500  (i = 1,2, 3,4), respectively. Furthermore, we find that the optimal value of ki  (i = 1,2, 3,4) is about 750. And the more the parameters are close to 750, the shorter the time will be required for synchronization of the drive system and response system, the better the effect of synchronization will be.

4.2. Synchronization of the Fractional-Order Hyperchaotic Lorenz System

Lorenz system can be described as follows [26]:
()
When a = 10, b = 8/3, and c = 28, this system exhibits a chaotic behavior. X. Y. Wang and M. J. Wang [19] add a nonlinear controller x4 to the first equation of Lorenz system, and let , then a new system is obtained as follows:
()
When a = 10, b = 8/3, c = 28, and r = −1, the system exhibits a hyperchaotic behavior. Wang and Song [20] consider the 4D fractional-order Lorenz system which can be described as
()
When we select the parameters as a = 10, b = 8/3, c = 28, r = −1, and α = 0.98, the system (41) is hyperchaotic [20]. Now, we select the order α = 0.99 and initial value (2, −2,1, −1), the system exhibits hyperchaotic behavior, as shown in Figure 4.
Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
Hyperchaotic attractors in the fractional-order hyperchaotic Lorenz system with α = 0.99. The panels (a) and (b) show the 3D views of x3 − x2 − x1 and x4 − x3 − x2, respectively.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
Hyperchaotic attractors in the fractional-order hyperchaotic Lorenz system with α = 0.99. The panels (a) and (b) show the 3D views of x3 − x2 − x1 and x4 − x3 − x2, respectively.
We consider the system (41) as a drive system, then the controlled response system is given by
()
where ki  (i = 1,2, 3,4) is control parameter and . According to system (41) and (42), the error system is obtained as follows:
()
When the control parameters ki  (i = 1,2, 3,4) and ωi  (i = 1,2, 3,4) satisfy the conditions of Theorem 2, the system (43) can be stabilized to the original point; that is, synchronization of systems (41) and (42) is achieved.

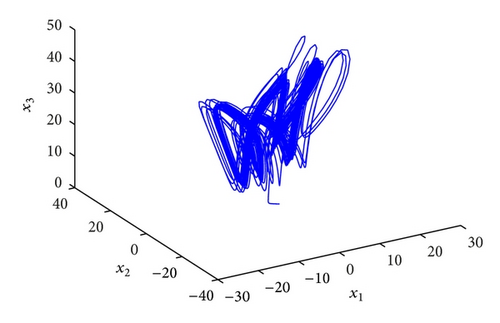
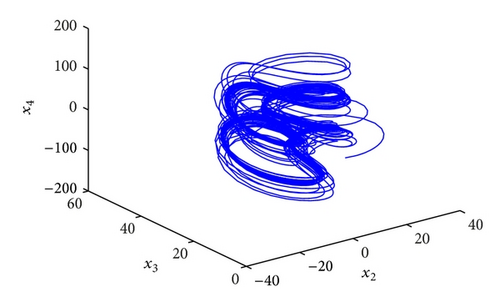
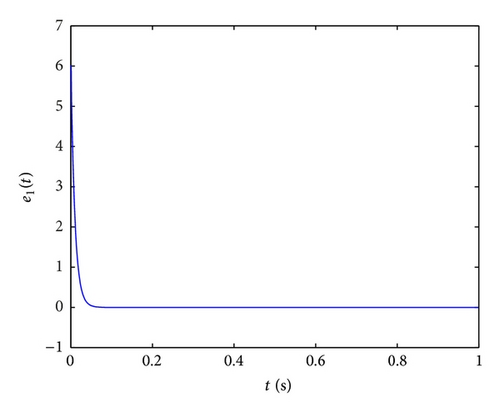
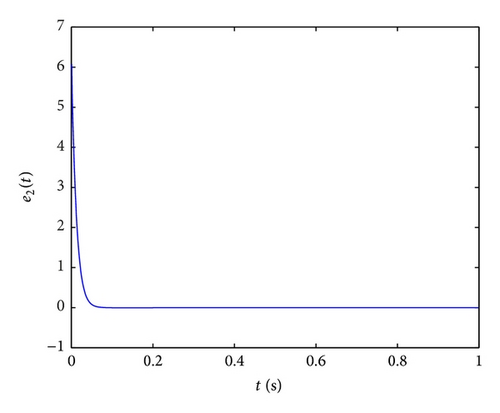
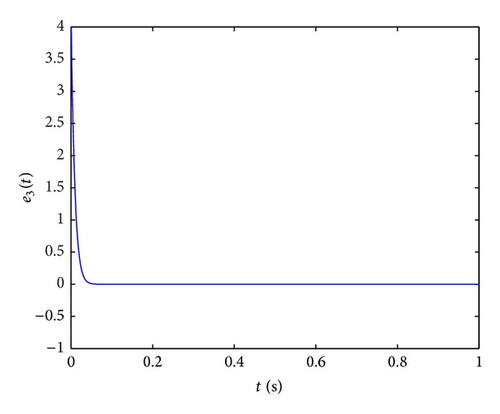
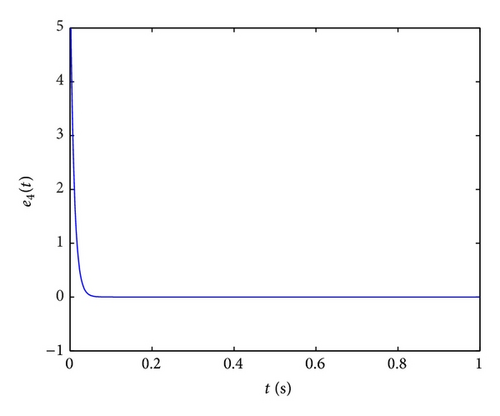
In order to implement this controller easily, we also select the parameters k1 = k2 = k3 = k4 = 100, ω1 = ω2 = ω3 = ω4 = 1 and initial values x(0) = (−2, −2, −1, −1), y(0) = (4,4, 5,5), u(0) = 0; the numerical results, illustrated in Figure 5, show that the error system (43) is driven to original point; that is, the systems (41) and (42) are synchronized. From Figure 5, two systems are synchronized about at 0.05 s, which demonstrates that the fractional-order controller can synchronize the Lorenz system very effectively and fast.

Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
Time waveforms of synchronization errors e1 (a), e2 (b), e3 (c), and e4 (d) between two fractional-order hyperchaotic Lorenz systems.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
Time waveforms of synchronization errors e1 (a), e2 (b), e3 (c), and e4 (d) between two fractional-order hyperchaotic Lorenz systems.
Details are in the caption following the image
Figure 5 (c)
Open in figure viewerPowerPoint
Time waveforms of synchronization errors e1 (a), e2 (b), e3 (c), and e4 (d) between two fractional-order hyperchaotic Lorenz systems.
Details are in the caption following the image
Figure 5 (d)
Open in figure viewerPowerPoint
Time waveforms of synchronization errors e1 (a), e2 (b), e3 (c), and e4 (d) between two fractional-order hyperchaotic Lorenz systems.
To get an optimal value of the parameters ki  (i = 1,2, 3,4) which make the two hyperchaotic systems synchronize, we continuously increase the parameters k1 = k2 = k3 = k4, form 1 to 2000, in step 1. By the numerical simulations with same initial values, we find the following conclusion.
  • (i)

    When k1 = k2 = k3 = k4 < 4, two systems cannot achieve synchronization.

  • (ii)

    When 4 ≤ k1 = k2 = k3 = k4 < 30, two systems achieve synchronization, but the synchronization times are more than 1 s.

  • (iii)

    When 30 ≤ k1 = k2 = k3 = k4 ≤ 1902, two systems achieve synchronization very fast and the synchronization times are less than 1 s, which are shown in Figure 6(a).

  • (iv)

    When k1 = k2 = k3 = k4 > 1902, two systems cannot achieve synchronization.

Details are in the caption following the image
Figure 6 (a)
Open in figure viewerPowerPoint
The waveform of synchronization time with the control parameters ki  (i = 1,2, 3,4) (a) and time waveforms of synchronization errors between two hyperchaotic Lorenz systems with parameter ki = 10 (b), 750(c), 1800 (d) (i = 1,2, 3,4), respectively.
Details are in the caption following the image
Figure 6 (b)
Open in figure viewerPowerPoint
The waveform of synchronization time with the control parameters ki  (i = 1,2, 3,4) (a) and time waveforms of synchronization errors between two hyperchaotic Lorenz systems with parameter ki = 10 (b), 750(c), 1800 (d) (i = 1,2, 3,4), respectively.
Details are in the caption following the image
Figure 6 (c)
Open in figure viewerPowerPoint
The waveform of synchronization time with the control parameters ki  (i = 1,2, 3,4) (a) and time waveforms of synchronization errors between two hyperchaotic Lorenz systems with parameter ki = 10 (b), 750(c), 1800 (d) (i = 1,2, 3,4), respectively.
Details are in the caption following the image
Figure 6 (d)
Open in figure viewerPowerPoint
The waveform of synchronization time with the control parameters ki  (i = 1,2, 3,4) (a) and time waveforms of synchronization errors between two hyperchaotic Lorenz systems with parameter ki = 10 (b), 750(c), 1800 (d) (i = 1,2, 3,4), respectively.

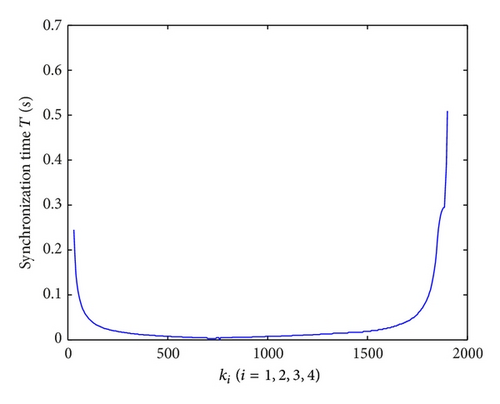
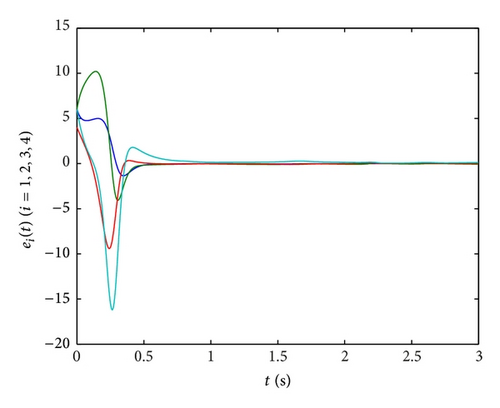
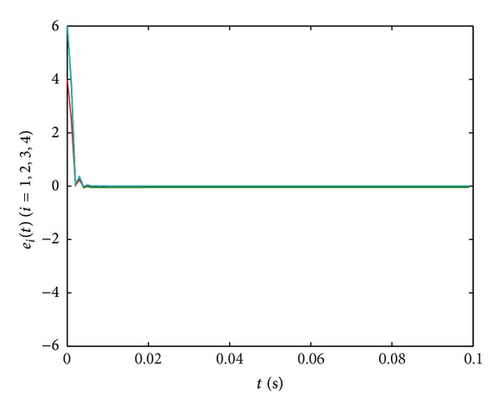
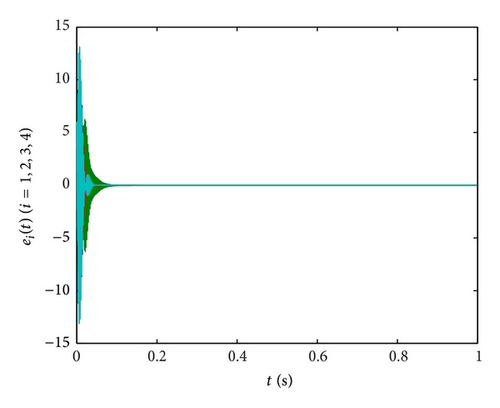
In Figures 6(b)–6(d), the time evolutions of the error functions between systems (41) and (42) are given with ki = 10,750,1800  (i = 1,2, 3,4), respectively. Furthermore, we find that the optimal value of ki  (i = 1,2, 3,4) is about 750. And the more the parameters are close to 750, the shorter the time will be required for synchronization of the drive system and response system, the better the effect of synchronization will be.

4.3. Synchronization of the Fractional-Order Hyperchaotic Lü System

In 2006, Chen et al. [31] construct a new hyperchaotic system based on Lü system by using a state feedback controller. It is given by
()
where a, b, c are the constants of Lü system and d is a control parameter. When a = 36, b = 3, c = 20, and −0.35 < d ≤ 1.30, system (44) has a hyperchaotic attractor [31]. Then we consider the fractional version of this system which is given by
()
If we select the order α = 0.95, d = 1.30 and initial value (0.1,0.1,0.1,0.2), the system exhibits hyperchaotic behavior, as shown in Figure 7.
Details are in the caption following the image
Figure 7 (a)
Open in figure viewerPowerPoint
Hyperchaotic attractors in the fractional hyperchaotic Lü system with α = 0.95. The panels (a) and (b) show the 3D views of x3 − x2 − x1 and x4 − x3 − x2, respectively.
Details are in the caption following the image
Figure 7 (b)
Open in figure viewerPowerPoint
Hyperchaotic attractors in the fractional hyperchaotic Lü system with α = 0.95. The panels (a) and (b) show the 3D views of x3 − x2 − x1 and x4 − x3 − x2, respectively.
We consider the system (45) as a drive system, then the controlled response system is
()
where ki  (i = 1,2, 3,4) is control parameter and . According to systems (45) and (46), the error system is obtained as follows:
()
When the control parameters ki  (i = 1,2, 3,4) and ωi  (i = 1,2, 3,4) satisfy the conditions of Theorem 2, the system (47) can be stabilized to the original point; that is, the synchronization of systems (45) and (46) is achieved.

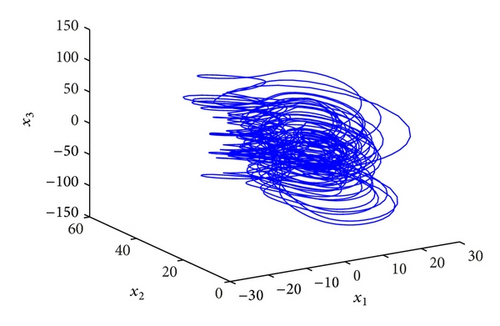
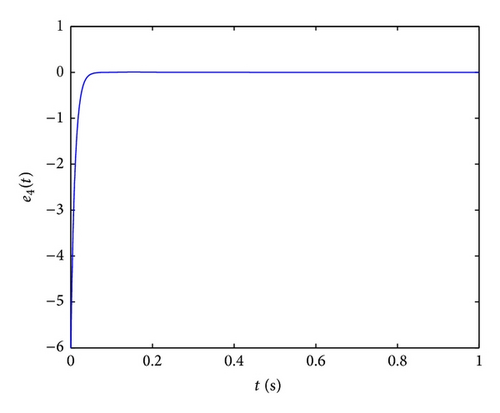
In order to implement this controller easily, we also select the parameters k1 = k2 = k3 = k4 = 100, ω1 = ω2 = ω3 = ω4 = 1 and initial values x(0) = (−2,2, −1,1), y(0) = (4, −4,5, −5), u(0) = 0; the numerical results, illustrated in Figure 8, show that the error system (47) is driven to original point; that is, the systems (45) and (46) are synchronized. From the Figure 8, we can obtain that two systems are synchronized about at 0.1 s, so the fractional-order controller can synchronize the Lü′s system very effectively and fast.

Details are in the caption following the image
Figure 8 (a)
Open in figure viewerPowerPoint
Time waveforms of synchronization errors e1 (a), e2 (b), e3 (c), and e4 (d) between two fractional-order hyperchaotic Lü systems.
Details are in the caption following the image
Figure 8 (b)
Open in figure viewerPowerPoint
Time waveforms of synchronization errors e1 (a), e2 (b), e3 (c), and e4 (d) between two fractional-order hyperchaotic Lü systems.
Details are in the caption following the image
Figure 8 (c)
Open in figure viewerPowerPoint
Time waveforms of synchronization errors e1 (a), e2 (b), e3 (c), and e4 (d) between two fractional-order hyperchaotic Lü systems.
Details are in the caption following the image
Figure 8 (d)
Open in figure viewerPowerPoint
Time waveforms of synchronization errors e1 (a), e2 (b), e3 (c), and e4 (d) between two fractional-order hyperchaotic Lü systems.
To get an optimal value of the parameters ki  (i = 1,2, 3,4) to make the two hyperchaotic systems synchronize, we continuously increase the parameters k1 = k2 = k3 = k4, form 1 to 4500, in step 1. By the numerical simulations with same initial values, we find the following conclusion.
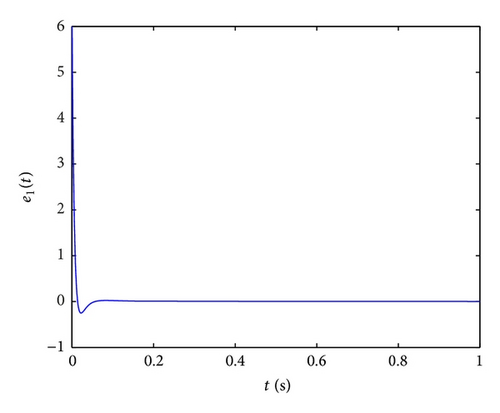
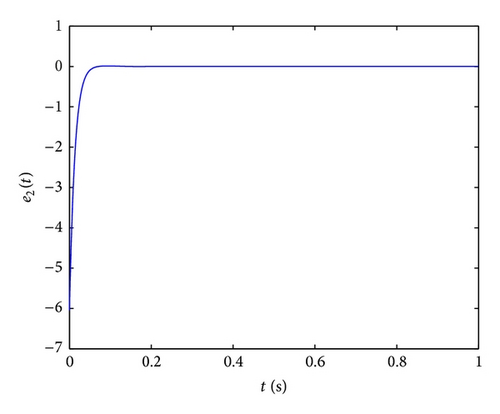
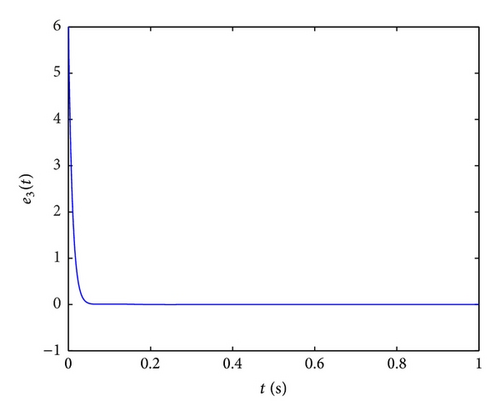
  • (i)

    When k1 = k2 = k3 = k4 < 10, two systems cannot achieve synchronization.

  • (ii)

    When 10 ≤ k1 = k2 = k3 = k4 < 205, two systems achieve synchronization, but the synchronization times are more than 0.1 s.

  • (iii)

    When 205 ≤ k1 = k2 = k3 = k4 < 4500, two systems achieve synchronization very fast and the synchronization times are less than 0.1 s, which are shown in Figure 9(a).

  • (iv)

    When k1 = k2 = k3 = k4 > 4500, two systems cannot achieve synchronization.

Details are in the caption following the image
Figure 9 (a)
Open in figure viewerPowerPoint
The waveform of synchronization time with the control parameters ki  (i = 1,2, 3,4) (a) and time waveforms of synchronization errors between two hyperchaotic Lü systems with parameter ki = 20 (b), 2000 (c), 4000 (d) (i = 1,2, 3,4), respectively.
Details are in the caption following the image
Figure 9 (b)
Open in figure viewerPowerPoint
The waveform of synchronization time with the control parameters ki  (i = 1,2, 3,4) (a) and time waveforms of synchronization errors between two hyperchaotic Lü systems with parameter ki = 20 (b), 2000 (c), 4000 (d) (i = 1,2, 3,4), respectively.
Details are in the caption following the image
Figure 9 (c)
Open in figure viewerPowerPoint
The waveform of synchronization time with the control parameters ki  (i = 1,2, 3,4) (a) and time waveforms of synchronization errors between two hyperchaotic Lü systems with parameter ki = 20 (b), 2000 (c), 4000 (d) (i = 1,2, 3,4), respectively.
Details are in the caption following the image
Figure 9 (d)
Open in figure viewerPowerPoint
The waveform of synchronization time with the control parameters ki  (i = 1,2, 3,4) (a) and time waveforms of synchronization errors between two hyperchaotic Lü systems with parameter ki = 20 (b), 2000 (c), 4000 (d) (i = 1,2, 3,4), respectively.

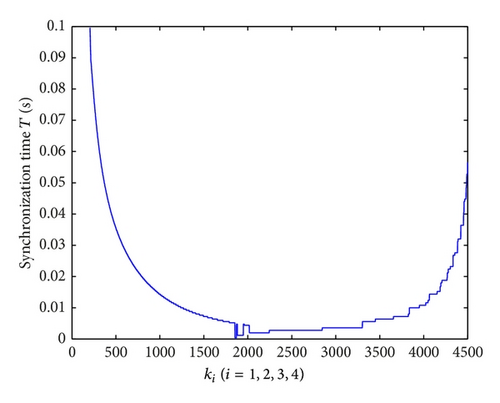
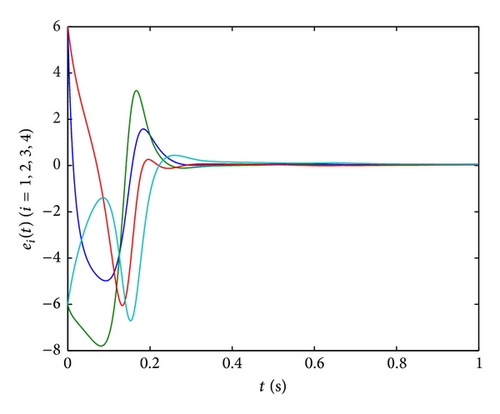
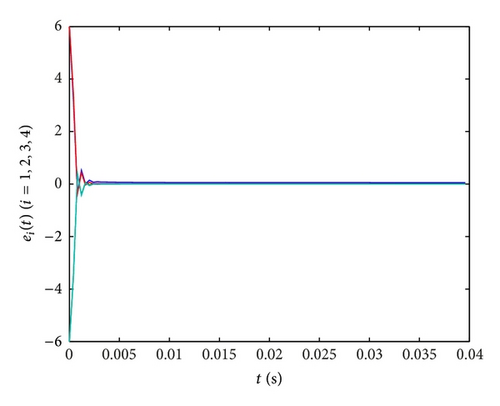
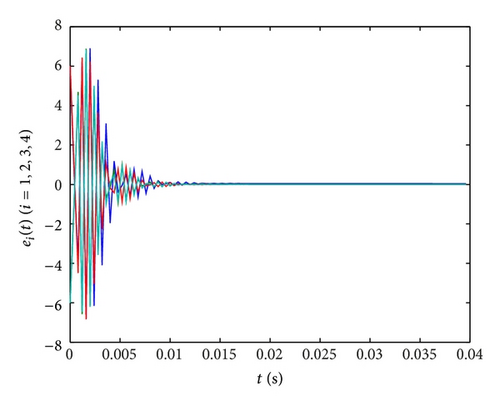
In Figures 9(b)–9(d), the time evolutions of the error functions between systems (45) and (46) are given with ki = 20,2000,4000  (i = 1,2, 3,4), respectively. Furthermore, we find that the optimal value of ki  (i = 1,2, 3,4) is about 2000. And the more the parameters are close to 2000, the shorter the time will be required for synchronization of the drive system and response system, the better the effect of synchronization will be.

4.4. Fractional-Order Control in the Presence of Measurement Noise

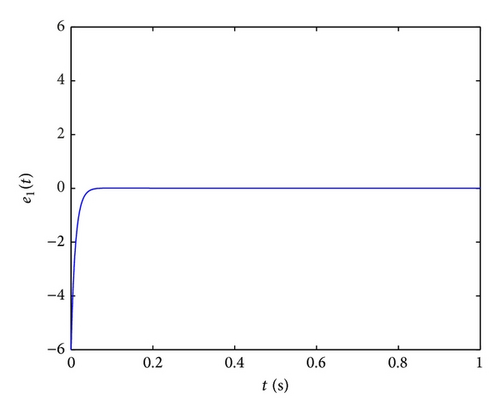
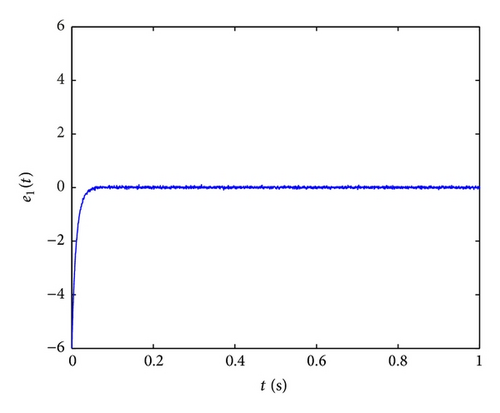
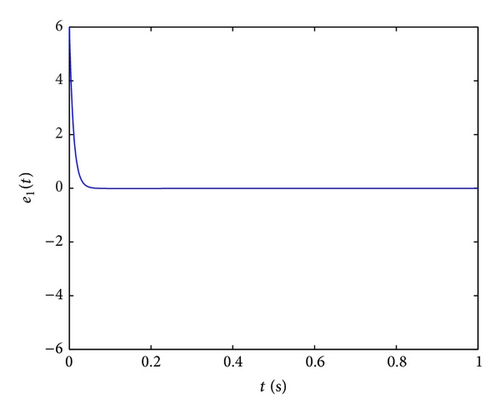
Further, in order to study the control performance of the proposed fractional-order controller in the presence of measurement noise, we add the white noise with variance D = 2 into the first formula of the controlled fractional-order hyperchaotic Chen system and Lorenz system. The control results of x1(t) without and with noise are given in Figures 10(a)–10(d), which show that the method can effectively filter out the out-of-band noise and thus reduce the noise effect on the control. This also shows the superiority of the proposed fractional-order controller.

Details are in the caption following the image
Figure 10 (a)
Open in figure viewerPowerPoint
Comparison of the time waveforms of synchronization errors e1(t) without and with noise, panels (a)-(b) and (c)-(d) show the results of the hyperchaotic Chen system and Lorenz system, respectively.
Details are in the caption following the image
Figure 10 (b)
Open in figure viewerPowerPoint
Comparison of the time waveforms of synchronization errors e1(t) without and with noise, panels (a)-(b) and (c)-(d) show the results of the hyperchaotic Chen system and Lorenz system, respectively.
Details are in the caption following the image
Figure 10 (c)
Open in figure viewerPowerPoint
Comparison of the time waveforms of synchronization errors e1(t) without and with noise, panels (a)-(b) and (c)-(d) show the results of the hyperchaotic Chen system and Lorenz system, respectively.
Details are in the caption following the image
Figure 10 (d)
Open in figure viewerPowerPoint
Comparison of the time waveforms of synchronization errors e1(t) without and with noise, panels (a)-(b) and (c)-(d) show the results of the hyperchaotic Chen system and Lorenz system, respectively.

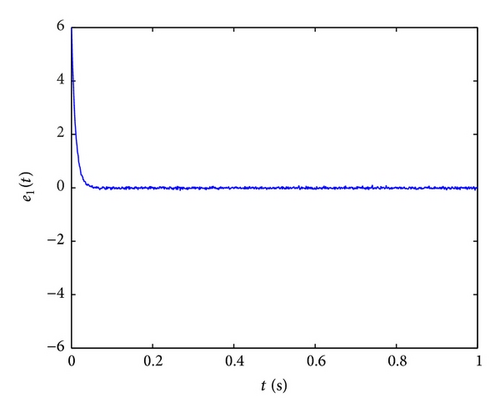
5. Conclusion

In conclusion, we proposed a fractional-order controller and presented a synchronization law for the 4D fractional-order hyperchaotic systems. According to the Lyapunov stability theorem of the fractional systems, the proposed method achieved to synchronize arbitrary 4D fractional-order hyperchaotic systems. Our proposed controller is very simple and could be easily realized experimentally. Furthermore, the present method is universal, that is, for almost all 4D fractional-order systems, and the controllers obtained are similar in form. Numerical simulation results of synchronization of the fractional-order hyperchaotic Chen system, the fractional-order hyperchaotic Lorenz system, and the fractional-order hyperchaotic Lü system demonstrate the effectiveness and the validity of the proposed method. And we give the optimal value of the parameters by numerical simulation. Furthermore, we have implemented and verified our method for other fractional-order hyperchaotic systems [21, 32, 33], namely, the generalized Henon-Heiles system [32], the Rössler system [21], the hyperchaotic Chua system [33], and so forth. The numerical simulation results indicated that the controller can make the fractional-order hyperchaotic systems synchronize very effectively and fast, and it provides a theoretical basis for the applications of synchronization in fractional hyperchaotic systems. In the future work, we will discuss the synchronization of hyperchaotic systems which have the different structure.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This work is supported by Artificial Intelligence Key Laboratory of Sichuan Province 2014RYJ05, The Opening Project of Sichuan Province University Key Laboratory of Bridge Non-Destruction Detecting and Engineering Computing 2013QYJ01, and Found of Sichuan University of Science and Engineering Grant nos. 2012PY17, 2012KY06.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.