Numerical Solutions of Two-Way Propagation of Nonlinear Dispersive Waves Using Radial Basis Functions
Abstract
We obtain the numerical solution of a Boussinesq system for two-way propagation of nonlinear dispersive waves by using the meshless method, based on collocation with radial basis functions. The system of nonlinear partial differential equation is discretized in space by approximating the solution using radial basis functions. The discretization leads to a system of coupled nonlinear ordinary differential equations. The equations are then solved by using the fourth-order Runge-Kutta method. A stability analysis is provided and then the accuracy of method is tested by comparing it with the exact solitary solutions of the Boussinesq system. In addition, the conserved quantities are calculated numerically and compared to an exact solution. The numerical results show excellent agreement with the analytical solution and the calculated conserved quantities.
1. Introduction
This work studies the numerical solution of this system by means of radial basis functions (RBFs). The use of these types of basis functions has become very popular in recent times; see for instance the work of Buhmann [11], Franke and Schaback [12], Driscoll and Heryudono [13], and the references therein. The main inspiration for this work is the very successful application of RBFs to solve the Kawahara equation [14] and the modified regularized long wave equation (MRLW) [15].
2. The Method of Lines for Radial Basis Functions
The RBFs approach is one of the most effective meshless methods to solve numerically PDEs. The key feature of the RBFs is that its implementation does not require a mesh at all. The method employs approximants whose values depend only on the distance between some center point and a domain point, in an appropriate norm. Due to the use of the distance functions, we can control the convergence up to an order proportional to the spacing of two points where we evaluate such functions [16].
The RK4 scheme does not have stability issues as long as the time step Δt is chosen sufficiently small. The selection of the time step is done by the following [18].
Rule of Thumbs. The method of lines is stable if the eigenvalues of the linearized spatial discretization operator, scaled by Δt, lie in the stability region of the time-discretization operator.
For the stability analysis nonlinearity in (22), F(t, y(t)) is set to zero and we compute the eigenvalues of M−1Γ. So the method is stable as long as the eigenvalues are in the stability region (−2.76 < Δtλj < 0). In order to have a stable scheme, we adjust the parameter φ so that the matrices remain in the region of stability. This was carried out in the numerical experiments.
3. Numerical Approximations of Boussinesq System
The integrals involving the conserved quantities were calculated by using the Trapezoidal rule.
3.1. Numerical Benchmark
| Method | φ | L2 error of v | L∞ error of v | Amplitude v | x |
|---|---|---|---|---|---|
| Analytic | — | — | — | 7.462309 | 37.43 |
| MQ | 1.23 | 3.074E − 05 | 2.721E − 05 | 7.462316 | 37.43 |
| G | 2.66 | 5.395E − 05 | 4.783E − 05 | 7.462310 | 37.43 |
| IQ | 1.00 | 2.244E − 03 | 2.129E − 03 | 7.462390 | 37.43 |
| IMQ | 2.05 | 2.450E − 03 | 1.224E − 03 | 7.462565 | 37.43 |
| Method | φ | L2 error of u | L∞ error of u | Amplitude (P-P) u | xmin | xmax |
|---|---|---|---|---|---|---|
| Analytic | — | — | — | 4.91342 | 36.23 | 37.43 |
| MQ | 1.23 | 3.381E − 05 | 2.606E − 05 | 4.91343 | 36.23 | 37.43 |
| G | 2.66 | 5.747E − 05 | 5.358E − 05 | 4.91339 | 36.23 | 37.43 |
| IQ | 1.00 | 2.313E − 03 | 2.204E − 03 | 4.91575 | 36.23 | 37.43 |
| IMQ | 2.05 | 2.804E − 03 | 1.950E − 03 | 4.91481 | 36.23 | 37.43 |
| Method | I1 | I2 | I3 | I4 |
|---|---|---|---|---|
| Analytic | 15.81139 | 0.0000 | 158.113 | −22.5876975726 |
| MQ | 15.81134 | −2.07E − 05 | 158.113 | −22.58776106781 |
| G | 15.81139 | −1.31E − 09 | 158.113 | −22.58776062211 |
| IQ | 15.81144 | −2.87E − 04 | 158.168 | −22.58432200892 |
| IMQ | 15.81156 | 6.92E − 04 | 158.152 | −22.58512792633 |
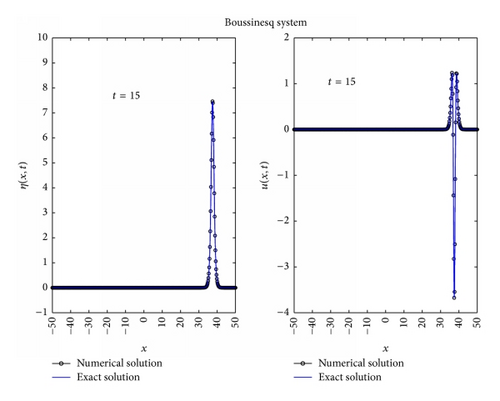
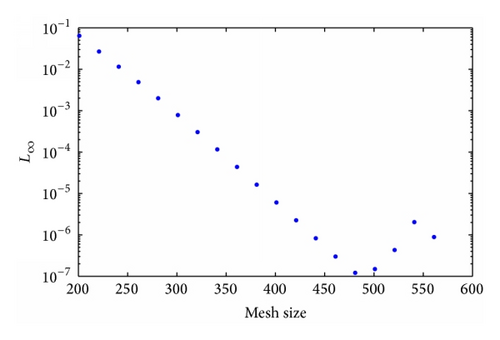
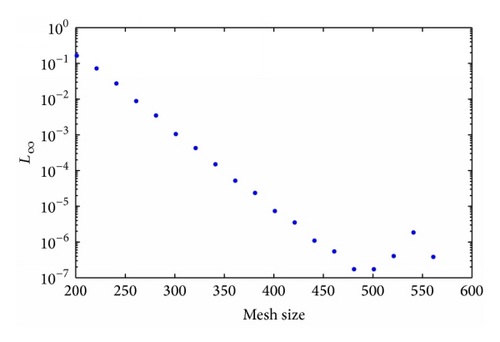
3.2. Problem
| Time | L2 error of v | L∞ error of v | L2 error of u | L∞ error of u | I1 | I2 |
|---|---|---|---|---|---|---|
| MQ | ||||||
| 0.5 | 3.467E − 08 | 4.122E − 08 | 4.437E − 08 | 5.202E − 08 | 1.7748239 | 1.6733200 |
| 1.0 | 1.544E − 07 | 1.766E − 07 | 1.892E − 07 | 2.231E − 07 | 1.7748238 | 1.6733198 |
| 2.0 | 3.061E − 07 | 3.130E − 07 | 3.372E − 07 | 3.550E − 07 | 1.7748235 | 1.6733196 |
| 3.0 | 3.960E − 07 | 3.480E − 07 | 4.206E − 07 | 3.796E − 07 | 1.7748233 | 1.6733193 |
| 4.0 | 4.585E − 07 | 3.600E − 07 | 4.762E − 07 | 3.825E − 07 | 1.7748231 | 1.6733195 |
| 5.0 | 4.501E − 07 | 3.490E − 07 | 4.604E − 07 | 3.689E − 07 | 1.7748232 | 1.6733192 |
| 10.0 | 4.758E − 07 | 2.765E − 07 | 4.881E − 07 | 2.864E − 07 | 1.7748237 | 1.6733193 |
| 15.0 | 5.607E − 07 | 2.351E − 07 | 5.715E − 07 | 2.400E − 07 | 1.7748246 | 1.6733198 |
| 20.0 | 7.205E − 07 | 2.102E − 07 | 7.300E − 07 | 2.138E − 07 | 1.7748260 | 1.6733205 |
| 25.0 | 1.116E − 06 | 3.704E − 07 | 1.143E − 07 | 3880E − 07 | 1.7748285 | 1.6733212 |
| 30.0 | 4.239E − 06 | 6.321E − 06 | 4.954E − 06 | 5.960E − 06 | 1.7748236 | 1.6733103 |
| Time | L2 error of v | L∞ error of v | L2 error of u | L∞ error of u | I1 | I2 |
|---|---|---|---|---|---|---|
| G | ||||||
| 0.5 | 2.268E − 10 | 1.442E − 10 | 2.188E − 10 | 1.425E − 10 | 1.7748239 | 1.6733200 |
| 1.0 | 4.548E − 10 | 2.948E − 10 | 4.351E − 10 | 2.877E − 10 | 1.7748238 | 1.6733198 |
| 2.0 | 9.045E − 10 | 5.976E − 10 | 8.672E − 10 | 5.848E − 10 | 1.7748235 | 1.6733196 |
| 3.0 | 1.343E − 09 | 9.038E − 10 | 1.295E − 09 | 8.901E − 10 | 1.7748233 | 1.6733193 |
| 4.0 | 1.775E − 09 | 1.195E − 09 | 1.710E − 09 | 1.172E − 09 | 1.7748231 | 1.6733195 |
| 5.0 | 2.194E − 09 | 1.476E − 09 | 2.113E − 09 | 1.445E − 09 | 1.7748232 | 1.6733192 |
| 10.0 | 4.065E − 09 | 2.570E − 09 | 3.909E − 09 | 2.490E − 09 | 1.7748237 | 1.6733193 |
| 15.0 | 5.600E − 09 | 3.353E − 09 | 5.371E − 09 | 3.232E − 09 | 1.7748246 | 1.6733198 |
| 20.0 | 6.900E − 09 | 3.976E − 09 | 6.601E − 09 | 2.821E − 09 | 1.7748260 | 1.6733205 |
| 25.0 | 2.992E − 08 | 4.345E − 08 | 2.668E − 08 | 4.097E − 08 | 1.7748285 | 1.6733212 |
| 30.0 | 4.193E − 06 | 6.322E − 06 | 3.718E − 06 | 5.960E − 06 | 1.7748236 | 1.6733103 |
| Time | L2 error of v | L∞ error of v | L2 error of u | L∞ error of u | I1 | I2 |
|---|---|---|---|---|---|---|
| IQ | ||||||
| 0.5 | 3.598E − 07 | 4.300E − 07 | 4.310E − 07 | 5.425E − 07 | 1.7748239 | 1.6733200 |
| 1.0 | 2.492E − 06 | 2.925E − 06 | 3.060E − 06 | 3.647E − 06 | 1.7748238 | 1.6733198 |
| 2.0 | 1.299E − 05 | 1.268E − 05 | 1.510E − 05 | 1.495E − 05 | 1.7748235 | 1.6733196 |
| 3.0 | 2.101E − 05 | 1.786E − 05 | 2.285E − 05 | 1.978E − 05 | 1.7748233 | 1.6733193 |
| 4.0 | 2.366E − 05 | 1.894E − 05 | 2.456E − 05 | 2.006E − 05 | 1.7748231 | 1.6733195 |
| 5.0 | 3.522E − 05 | 2.862E − 05 | 4.034E − 05 | 3.483E − 05 | 1.7748232 | 1.6733192 |
| 10.0 | 6.753E − 05 | 4.177E − 05 | 7.152E − 05 | 4.450E − 05 | 1.7748237 | 1.6733193 |
| 15.0 | 1.342E − 04 | 7.717E − 05 | 1.386E − 04 | 8.006E − 05 | 1.7748246 | 1.6733198 |
| 20.0 | 1.559E − 04 | 7.227E − 05 | 1.600E − 04 | 7.515E − 05 | 1.7748260 | 1.6733205 |
| 25.0 | 2.088E − 04 | 8.579E − 05 | 2.150E − 04 | 8.807E − 05 | 1.7748285 | 1.6733212 |
| 30.0 | 2.743E − 04 | 9.665E − 05 | 2.793E − 04 | 9.855E − 05 | 1.7748236 | 1.6733103 |
| Time | L2 error of v | L∞ error of v | L2 error of u | L∞ error of u | I1 | I2 |
|---|---|---|---|---|---|---|
| IMQ | ||||||
| 0.5 | 2.081E − 05 | 2.670E − 05 | 2.595E − 05 | 3.369E − 05 | 1.7748239 | 1.6733200 |
| 1.0 | 9.158E − 05 | 1.056E − 04 | 1.114E − 04 | 1.310E − 04 | 1.7748238 | 1.6733198 |
| 2.0 | 2.616E − 04 | 2.468E − 04 | 2.967E − 04 | 2.830E − 04 | 1.7748235 | 1.6733196 |
| 3.0 | 3.887E − 04 | 3.171E − 04 | 4.191E − 04 | 3.437E − 04 | 1.7748233 | 1.6733193 |
| 4.0 | 4.852E − 04 | 3.515E − 04 | 5.094E − 04 | 3.711E − 04 | 1.7748231 | 1.6733195 |
| 5.0 | 5.616E − 04 | 3.659E − 04 | 5.816E − 04 | 3.815E − 04 | 1.7748232 | 1.6733192 |
| 10.0 | 8.109E − 04 | 3.712E − 04 | 8.225E − 04 | 3.799E − 04 | 1.7748237 | 1.6733193 |
| 15.0 | 1.221E − 03 | 5.494E − 04 | 1.253E − 03 | 5.849E − 04 | 1.7748246 | 1.6733198 |
| 20.0 | 1.783E − 03 | 6.396E − 04 | 1.808E − 03 | 6.490E − 04 | 1.7748260 | 1.6733205 |
| 25.0 | 2.274E − 03 | 6.435E − 04 | 2.298E − 03 | 6.496E − 04 | 1.7748285 | 1.6733212 |
| 30.0 | 2.803E − 03 | 7.035E − 04 | 2.835E − 03 | 7.170E − 04 | 1.7748236 | 1.6733103 |
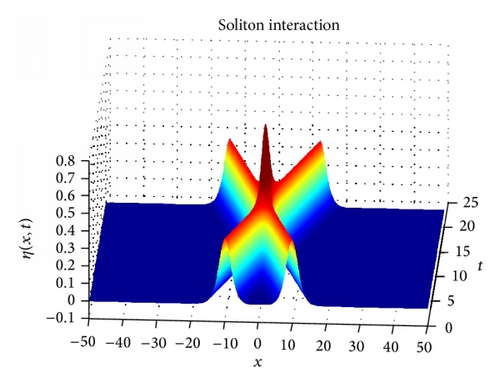
3.3. Problem
- (1)
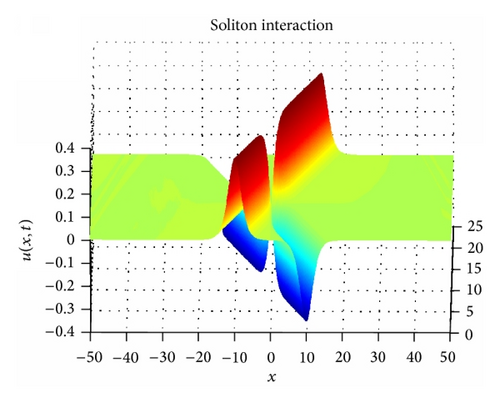
Solitons are permanent in form.
- (2)
Solitons are localized within a region.
- (3)
Solitons can interact with other solitons and emerge from the collision unchanged, except for a phase shift.
4. Conclusions
We have solved numerically the Boussinesq type system of nonlinear PDE by means of RBFs. In general this algorithm solves the system accurately. In particular, this method has optimal results for multiquadric and Gaussian radial basis functions. The conserved quantities were calculated and show good agreement with the analytical results. In the final section we ran a simulation for interacting solitons that is in agreement with the known properties of solitons. In conclusion the meshless method is shown to give good results for a system of PDEs having high order derivatives and mixed-partial derivatives.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.




