The online traffic signalization for intersection is addressed. A new model for intersection called positive switched system is presented. Then, based on the dissipativity analysis results for positive switched system, an online state-feedback control strategy for traffic signal in two-phase intersection section is proposed. A numerical example is provided to illustrate the effectiveness of our theoretical findings. Finally, in order to extend to more general cases, multiphase intersection is considered, and general dissipativity-based control is presented.

1. Introduction

Traffic signal control is a long-lasting research problem in urban transportation network system [1–3]. The effectiveness of a traffic signal system can reduce the incidence of delays, stops, fuel consumption, emission of pollutants, and accidents. Moreover, due to the rapid growth of traffic congestion, an effective traffic signalization plays an important role of relieving the oversaturated situation such as related articles [1, 4–11] and references cited therein. Most of the signal control strategies are based on fixed-time signal control [1, 4–7]. However, since the fixed-time strategies are based on historical data rather than real-time data, they are only applicable in undersaturated traffic conditions. In a few recent papers, some online signalization methods have been proposed [2, 8–13], which are more adaptive to the real-time traffic conditions. As for oversaturated condition, some significant results have been reported. For example, in [9], an optimal traffic light switching scheme was presented. Generally, it resorts to a minimization problem over a set of an extended linear complementarity problem, which is not an easy task when switching cycles is large. And concerned with recent notable result [10], a dissipative idea is applied into traffic signal design problem; a state feedback controller based on dissipativity-based control is derived. This dissipative approach provides a new insight on traffic signalization problem and intersection system. In our paper, we follow the dissipative idea and further exploit the positivity and switched properties of intersection system, which leads to a positive switched system approach into the dissipativity-based control framework. The particular class of hybrid system called positive switched system is used to model the intersection system.

Switched system can be efficiently used to model many practical systems which are inherently multimodel in the sense that several dynamical systems are required to describe their behavior. For more details of the recent results on the basic problems in stability and stabilization for switched systems, the reader is referred to survey papers [14–24] and the references cited therein. Moreover, positive switched system refers to the variables of system which are always confined to the positive orthant. Due to the obvious switched and positive characteristic of intersection system with traffic signal, the positive switched system is an appropriate model for it, but as far as we know, there exists no result based on the model of positive switched system. Thus, in our paper, we first set up a positive switched system model for two-phase intersection system, which is shown to be able to be modeled as a positive switched system with two subsystems. Then, a dissipativity-based control strategy is proposed by solving a set of linear programming (LP) problem which can be efficiently solved with aid of existing software toolbox. Then, an extension from two-phase intersection to multiphase intersection system is presented to meet more general cases.

The rest of this paper is organized as follows. In Section 2 the system model and problem formulation are introduced; dissipativity analysis for positive switched system is proposed in Section 3. The dissipativity-based control solution for two-phase intersection is given in Section 4. In Section 5 the results are extended to multiphase cases. Conclusions are given in Section 6.

Notations. The notations used in this paper are fairly standard. The superscript “T” stands for matrix transposition, denotes the n dimensional Euclidean space, and represents the set of nonnegative integers. In addition, in symmetric block matrices, we use * as an ellipsis for the terms that are introduced by symmetry. The notation A≻0 (A⪰0) means all the elements a_ij > 0 (a_ij ≥ 0), where a_ij denotes the element in the (i, j) position of A.

2. System Description and Problem Formulation

2.1. System Description and Modeling

The urban transportation system is composed of a network of intersections. Generally, an intersection is operated by a traffic signal that decides the movements of vehicles to pass the intersections or to stop to generate the queues. The movement may include vehicles going straight, turning left, turning right, or a combination of them.

In order to show our control idea clearly, we first consider the single intersection with four approaches and the traffic signal which has two phases, which are illustrated by Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Intersection with four approaches and two-phase signal.

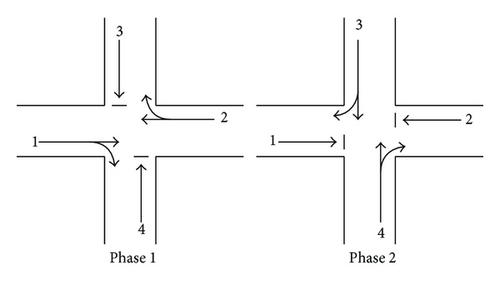
It is noted that the movements 1 and 2 are supposed to have same characteristics, and same consideration holds for movements 3 and 4.

Considering the transportation status at the time of the traffic signal turning from one phase to another, and denoting the time instant as k, , we are going to model the intersection system described in Figure 1; several useful definitions are introduced as follows.

Green Time g_p(k). It is the time for the movements for the successively activated phase p, , which is the control input signal required to be determined at each instant k for the intersection. It is assumed that there exists a g_p,max⁡ such that 0 ≤ g_p(k) ≤ g_p,max⁡.

Lost Time L. Lost time is defined as a period that is not used effectively in each phase by incoming traffic flow through an intersection, such as the start-up delay. Lost time is generally considered constant.

Effective Green Time . It is the time actually available for movement for phase p. Obviously, we can obtain , .

Input Flow Rate q_i. It is the input flow rate for movement i, .

Saturation Flow Rate s_i. It is the saturation flow rate for the movement i, , which is defined as the maximum number of vehicles being able to use the intersection without interruption during the effective green time.

The Number of Arrivals A_i,T. It is the number of vehicles joining the movement i during the time T. It can be figured out as A_i,T = q_iT.

The Number of Departures D_i,T. It is the number of vehicles departing from the movement i during the time T, which can be calculated by D_i,T = s_iT.

Queue Length x_i(k). It is the queue length of movement i, , at time instant k. It is assumed that the value of queue length x_i (number of vehicles) can be measured in real time, which can be obtained when video detection systems are utilized; otherwise, the local occupancy measurements o_i, collected in real time by traditional detector loops, can be transformed into (approximate) numbers of vehicles via suitable nonlinear functions x_i = f_i(o_i) such as in [3].

Moreover, since the congestion situation is not considered in our model, the queue lengths are always beneath their capacities, which is denoted by x_i,max⁡, . Thus, queue length x_i belongs to the region of admissible states as X_i = {x∣0 ≤ x_i ≤ x_i,max⁡}.

Based on the above definitions, we are now in the position to model the intersection system. Since there are two phases, it is natural that there are two dynamics for Phases 1 and 2, respectively.

Phase 1. The queue length x_i(k) evolves according to . For movements 1 and 2 which have same characteristics, it is obtained that , i = 1,2, and , i = 1,2; we have the following equation in Phase 1:

()

And for movements 3 and 4, since the movement is stopped which implies , i = 3,4, and , i = 3,4, it is obtained that

()

Phase 2. Following the same guideline in Phase 1, the following evolution equations can be derived:

()

Among the two subsystems concerned with two phases, there is a switching signal σ(k) determining which subsystem is activated at each instant k. Define

()

Augmenting the dynamics in Phases 1 and 2, the above equations can be restated as a switched system composed of two subsystems in state space form

()

where

()

Obviously, since the phases work in turns in the intersection system model, the switching signal σ(k) is defined as

()

which implies that the switching occurs at each instant k.

The most reported model is considered to have a fixed cycle (one repetition of the basic series of signal phases combinations at a junction), which has to be prespecified appropriately, and an inappropriate choice of cycle could lead to a bad control performance. On the other hand, there is no cycle time constraint in our switched system model, or no cycle time has to be designed previously; only controllable green time needs to be considered.

2.2. Control Problem Formulation

The purpose of our control is to relieve the oversaturated queue by the traffic signal. With the controllable green time g_p,

, we are going to design a state feedback controller in the form of

()

where K_p,

, is the feedback gains needed to be determined. Substituting state feedback controller (8) into system model (5), the closed loop of intersection system is expressed as

()

where A_p = I + B_pK_p. Under the control of (8), our design objective is to render the system (9) nonaccumulative with flux supply rate.

At first, the lengths of queue x_i(k),

, are supposed to be nonnegative in the evolution according to the system dynamics given any initial x_i(0) ≥ 0. Thus, to ensure the availability of designed state feedback controller, the positivity of x(k) has to be preserved during the time; that is,

()

Then, to make the system nonaccumulative, a particular copositive storage function indicating the total lengths of the movement stored in the system is introduced as

()

where

. The flow of vehicles supplied to the system is the total arrivals in each phase described by

()

And the total of departures in Phase 1 is D₁ = (s₁ + s₂)(g₁ − L) = (s₁ + s₂)g₁ − (s₁ + s₂)L and D₂ = (s₃ + s₄)(g₂ − L) = (s₃ + s₄)g₂ − (s₃ + s₄)L is for Phase 2. Thus, the flow of vehicles extracted from the system is

()

where d₁ = s₁ + s₂ and d₂ = s₃ + s₄. The flux supply rate in each phase can be defined as

()

that is,

()

where

and β_p = d_pL. To achieve a nonaccumulative system with storage function S(k) and supply rate θ(k), the following condition has to be satisfied:

()

which implies that the variation in the total queue length of the system is always less than or equal to the input flux minus the output flux. In this case the system with feedback controller (8) is nonaccumulative with respect to the flux supply rate θ(k).

3. Dissipativity Analysis for Positive Switched System

In this section, we will investigate the dissipativity of switched positive system, which plays the key role in solving the control problem for intersection system.

Consider the following switched positive system composed by P subsystems:

()

where

is the state vector, A_p and C_p are constant matrices with appropriate dimensions, and the switching law among subsystems is considered arbitrary.

Definition 1. System (1) is said to be positive if and only if, for any initial condition x(0)⪰0, the corresponding trajectory x(k)⪰0 holds for all .

Lemma 2. System (1) is positive if and only if A_p⪰0 and C_p⪰0, .

Proof. The sufficient part is obvious. We consider the necessity. Denote

()

we have

()

Since system (17) is positive, we can obtain

()

Hence, A_p⪰0 and C_p⪰0,

Definition 3. System (1) with supply rate , where α_p are vectors with appropriate dimensions and β_p are scalars, is said to be dissipative (strictly dissipative) if there exists a nonnegative function with S(0) = 0, called the storage function such that ΔS(k) ≤ θ(k) (ΔS(k) < θ(k)).

Remark 4. In strictly dissipative case, ΔS(k) < θ(k) can be expressed as ΔS(k)≤−ρS(k) + θ(k), where ρ > 0 provides a degree of freedom in choosing the quantity that we wish to dissipate. And if we enforce ρ = 0, it becomes the dissipative case. Hence, in the rest of paper, we consider the general dissipative performance satisfying ΔS(k)≤−ρS(k) + θ(k), where ρ ≥ 0.

For switched positive system, the switched copositive function , where h_p⪰0, ∀p ∈ P, can serve as a storage function. Then, the following theorem can be derived for the dissipativity of switched positive system (17) with respect to the particular supply rate .

Theorem 5. Consider switched positive system (17), given a scalar ρ ≥ 0. If there exists a set of vectors h_p⪰0, ∀p ∈ P, such that the following condition holds:

()

then switched positive system (17) is dissipative with respect to a supply rate

Proof. Given a set of vectors h_p⪰0, , the following switched copositive function is constructed:

()

By the definition of dissipativity and supply rate , we have to demonstrate the following inequality:

()

which ensures ΔS(k)≤−ρS(k) + θ(k). As this has to be satisfied for arbitrary switching signals, it follows that (23) has to hold for any special configuration

()

and for all nonzero

. Hence (23) means

()

Using the system model as x(k + 1) = A_px(k) + C_p, one has

()

From (21), it is easy to see that (26) is satisfied, which implies ΔS(k)≤−ρS(k) + θ(k) and the dissipativity of system (17).

Theorem 5 provides us with a switched copositive function method in search for a set of vectors h_p, . If we particularly choose a common vector h = h_p, , the following corollary can be obtained.

Corollary 6. Consider switched positive system (17), given a scalar ρ ≥ 0. If there exists a vector h⪰0 such that the following condition holds:

()

then switched positive system (17) is dissipative with respect to supply rate

Proof. Let h = h_p, in Theorem 5; Corollary 6 can be proved.

Remark 7. It is obvious to see that conditions in Theorem 5 are less conservative than Corollary 6 due to the explicit fact that a common storage function yields more conservative results than multiple storage function. But, in order to meet the actual intersection system, a common storage function S(k) = e^Tx(k), where , is particularly chosen to describe the total lengths of the movement stored in the system; thus Corollary 6 will be used to solve the control problem for intersection system.

4. Control Solution for Two-Phase Intersection

Now, based on the formulated control problem and analysis results in previous section, considering the two-phase intersection system, the feedback controller (8) has to be designed in which the state feedback gains K_p, , are the feedback gains needed to be determined. As what is discussed, to achieve a nonaccumulative closed loop with an available feedback controller, the design objective can be summarized as the following three points should be satisfied.

(1) Positivity. To ensure the availability of the feedback control in actual applications, we have that x(k)⪰0 holds for all and any x(0)⪰0, that is, preserving the positivity of closed loop.

(2) Dissipativity. Given the storage function S(k) = e^Tx(k), where , the closed loop should be dissipative with respect to supply rate , where α_p and β_p are defined in (15), which makes the intersection system nonaccumulative.

(3) Control Constraint. The constraint on the green time has to be satisfied to avoid unacceptable stop time for drivers in other approaches. By 0 ≤ g_p(k) ≤ g_p,max⁡ and g_p(k) = u_p(k) = K_px(k), the following constraint must be satisfied 0 ≤ K_px(k) ≤ g_p,max⁡.

Considering the closed loop system (9), the first point concerned with positivity can be solved through Lemma 2 for the switched positive system; that is, A_p⪰0,

, and C_p⪰0,

, should be satisfied. Obviously C_p⪰0, ∀p ∈ P, is automatically satisfied for two-phase intersection system since s_p > 0,

and L > 0. Moreover, A_p⪰0 can be rewritten as

()

to preserve positivity of feedback closed loop system.

Then, the second point on dissipativity can be solved by Corollary 6 where the common vector is chosen as

. Firstly, we have

()

Thus, it yields that e^TC_p − β_p ≤ 0,

, is satisfied for intersection system.

Moreover, to ensure dissipativity, the following condition has to be satisfied:

()

where

, d₁ = s₁ + s₂, and d₂ = s₃ + s₄.

At last, the constraint on the feedback is considered. Note that queue length x_i belongs to the region of admissible states as ; we denote set , where . Given any and 0 ≤ α ≤ 1, we have 0⪯αx₁ + (1 − α)x₂⪯x_max⁡, so is a convex set with 16 vertices which are denoted as v₁, v₂, …, v₁₆.

Furthermore, the constraint set on the green time can be expressed by set

. Since

is convex, we only need to check that the vertices v₁, v₂, …, v₁₆ are included in control constraint U_p; that is,

()

Summarizing above discussion, a solution for nonaccumulative feedback control is presented as follows.

Proposition 8. Consider the two-phase intersection system (5), given a scalar ρ ≥ 0. If there exist two feedback gains K₁ and K₂ such that

()

where vectors α_p and v_i are defined in (15) and (31), respectively, the green times chosen as g_p(k) = K_px(k),

, can guarantee the nonaccumulative performance of the closed loop system (9).

Remark 9. In actual applications, a lower boundary for the effective green time has to be selected as g_p,min⁡, thus the operation of the controller for each k is considered in the following form:

()

Here, it should be noted that since x(k) decrease along with the time to relieve the oversaturated queue, g_p(k) will finally converge to g_p,min⁡. Thus, g_p,min⁡ can be often chosen as an appropriate time for undersaturated situations.

Remark 10. Proposition 8 is an LP problem, which can be numerically solved by the LP optimal toolbox.

Example 11. Consider a two-phase intersection as s₁ = 0.4 veh/s, s₂ = 0.6 veh/s, s₃ = 0.7 veh/s, and s₄ = 0.6 veh/s, q₁ = 0.2 veh/s, q₂ = 0.1 veh/s, q₃ = 0.15 veh/s, and q₄ = 0.25 veh/s, and g_p,max⁡ = 100 s, g_p,min⁡ = 50 s. Given an initial oversaturated queue , the simulation results are shown in Figure 2.

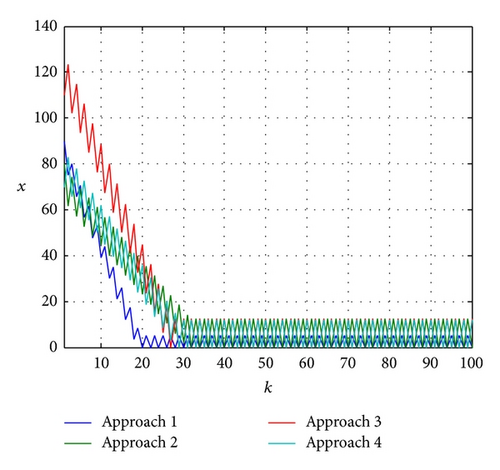
From the simulation results in Figure 2, we see that the oversaturated situation can be relieved by state feedback control, and we see that, after k = 30, the intersection runs in an undersaturated situation.

5. Extension to Multiphase Intersection

In this section, the results in previous section based on dissipativity and positivity of positive switched system will be generalized to multiphase intersection. At first, the system model for multiphase intersection will be presented as follows.

It is assumed that there exist P phases for the intersection with n movements. Hereby, the following sets are defined. For each phase , concerned with movements, we define , the activated movement set , and unactivated movement set ; similarly we have and .

In accordance with the modeling procedure for two-phase intersection, in each phase

, the queue length of movements x_i(k),

, evolves according to

()

Similar to the derivation of two-phase intersection model, we have

()

Thus, the evolution of movement

in phase

is described as follows:

()

With a switching signal σ(k) among subsystems

, define η_p(k) same as in (4). The above equations can be restated in state space form

()

where

()

The phases are working in turns in the intersection system model; the switching signal σ(k) is defined as

()

which implies that the switching occurs at each instant k.

With the aid of state feedback control as

()

the closed loop of intersection system is expressed as follows:

()

where A_p = I + B_pK_p.

Furthermore, following philosophy of positive and dissipative control for intersection in previous section, the positivity, dissipativity, and control constraint are guaranteed by the following steps.

Positivity. Based on Lemma 2, it is easy to see that the following condition is required to ensure the positivity:

()

Dissipativity. Since the storage function is S(k) = e^Tx(k), where

, and supply rate is

()

where

and

. Furthermore, by letting

, β_p = d_pL, where

, we get

, we can obtain e^TC_p − β_p ≤ 0,

, for multiphase intersection. Then, on the basis of Corollary 6, given a scalar ρ ≥ 0, the following condition should be satisfied to ensure the dissipativity:

()

Control Constraint. Each movement x_i belongs to

, and define convex set as

, where

; it is easy to see that there are N = n² vertices of

which are denoted as v₁, v₂, …, v_N. From the constraint set on the green time by set

, the following condition has to be satisfied:

()

Summarizing the above steps, the nonaccumulative feedback control solution multiphase intersection is presented as follows.

Proposition 12. Consider the P-phase intersection system (37), given a scalar ρ ≥ 0. If there exist p feedback gains K_p, , such that

()

where vectors α_p and v_i are defined in (44) and (45), respectively, the green times chosen as g_p(k) = K_px(k),

, can guarantee the nonaccumulative performance of the closed loop system (41).

6. Conclusions

By modeling the intersection into positive switched system, a dissipativity-based control strategy is proposed for online traffic signalization in this paper. Through fulfilling the positivity, dissipativity, and control constraint, an LP problem based design method is presented. A numerical example is provided to illustrate our results, and, furthermore, the two-phase intersection results are extended to multiphase intersection. The positive switched system approach provides us with a new insight on modeling intersection; introducing other advanced control schemes from positive switched system to intersection system is our future work.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Kaltenbach M. and Koivo H., Modelling and control of urban traffic flow, Proceedings of the Joint Automatic Control Conference, 1974, Houston, Tex, USA, University of Texas, 147–154.
Google Scholar
2 Tangsheng Y., On line traffic signalization using robust feedback control [Ph.D. thesis], 1997, Faculty of the Virginia Polytechnic Institute and State University, Virginia, Va, USA.
Google Scholar
3 Diakaki C., Papageorgiou M., and Aboudolas K., A multivariable regulator approach to traffic-responsive network- Wide signal control, Control Engineering Practice. (2002) 10, no. 2, 183–195, https://doi.org/10.1016/S0967-0661(01)00121-6, 2-s2.0-0036470455.
10.1016/S0967-0661(01)00121-6
Web of Science® Google Scholar
4 Gazis D., Optimal control of a system of oversaturated intersections, Operations Research. (1964) 12, 815–831.
10.1287/opre.12.6.815
Web of Science® Google Scholar
5 Gazis D. and Potts R., The oversaturated intersection, Proceedings of the 2nd International Symposium on the Theory of Road Traffic Flow Organization for Economic Cooperation and Development, 1965, Paris, France, 221–237.
Google Scholar
6 Green D., Control of oversaturated intersections, Operational Research Quarterly. (1967) 18, no. 2, 161–173, https://doi.org/10.2307/3007527.
10.1057/jors.1967.27
Google Scholar
7 D′Ans G. C. and Gazis D. C., Optimal control of oversaturated store-and-forward transportation networks, Transportation Science. (1976) 10, no. 1, 1–19, MR0416542, 2-s2.0-0016921209.
10.1287/trsc.10.1.1
Google Scholar
8 Chang T. and Lin J., Optimal signal timing for an oversaturated intersection, Transportation Research Part B. (2000) 34, no. 6, 471–491, https://doi.org/10.1016/S0191-2615(99)00034-X, 2-s2.0-0034083169.
10.1016/S0191-2615(99)00034-X
Web of Science® Google Scholar
9 de Schutter B. and de Moor B., Optimal traffic light control for a single intersection, European Journal of Control. (1998) 4, no. 3, 260–276, https://doi.org/10.1016/S0947-3580(98)70119-0, 2-s2.0-0032318345.
10.1016/S0947-3580(98)70119-0
Web of Science® Google Scholar
10 Motawej F., Bouyekhf R., and El Moudni A., A dissipativity-based approach to traffic signal control for an over-saturated intersection, Journal of the Franklin Institute. (2011) 348, no. 4, 703–717, https://doi.org/10.1016/j.jfranklin.2011.01.012, ZBL1214.90029, 2-s2.0-79953040902.
10.1016/j.jfranklin.2011.01.012
Web of Science® Google Scholar
11 Boillot F., Blosseville J. M., Lesort J. B., Motyka V., Papageorgiou M., and Sellam S., Optimal signal control of urban traffic networks, Proceedings of the 6th IEE International conference on Road Traffic Monitoring and Control, April 1992, London, UK, 75–79, 2-s2.0-0027041338.
Google Scholar
12 Dion F. and Yagar S., Real-time control of signalized networks different approaches for different needs, Proceedings of the 8th IEE International Conference on Road Traffic Monitoring and Control, 1996, London, UK, 56–60.
Google Scholar
13 Hunt P. B., Robertson D. I., and Bretherton R. D., The SCOOT on-line traffic signal optimisation technique, Traffic Engineering & Control. (1982) 23, no. 4, 190–192, 2-s2.0-0019899060.
Google Scholar
14 Decarlo R. A., Branicky M. S., Pettersson S., and Lennartson B., Perspectives and results on the stability and stabilizability of hybrid systems, Proceedings of the IEEE. (2000) 88, no. 7, 1069–1082, https://doi.org/10.1109/5.871309, 2-s2.0-33646910241.
10.1109/5.871309
Web of Science® Google Scholar
15 Lin H. and Antsaklis P. J., Stability and stabilizability of switched linear systems: a survey of recent results, IEEE Transactions on Automatic Control. (2009) 54, no. 2, 308–322, https://doi.org/10.1109/TAC.2008.2012009, MR2491959, 2-s2.0-61349147303.
10.1109/TAC.2008.2012009
Web of Science® Google Scholar
16 Xiang W. and Xiao J., Stabilization of switched continuous-time systems with all modes unstable via dwell time switching, Automatica. (2014) 50, no. 3, 940–945, https://doi.org/10.1016/j.automatica.2013.12.028, MR3173995.
10.1016/j.automatica.2013.12.028
Web of Science® Google Scholar
17 Xiang W. and Xiao J., Convex sufficient conditions on asymptotic stability and gain performance for uncertain discrete-time switched linear systems, IET Control Theory & Applications. (2014) 8, no. 3, 211–218, https://doi.org/10.1049/iet-cta.2013.0409, MR3185346.
10.1049/iet-cta.2013.0409
Web of Science® Google Scholar
18 Xiang W. and Xiao J., H_∞ finite-time control for switched nonlinear discrete-time systems with norm-bounded disturbance, Journal of the Franklin Institute. (2011) 348, no. 2, 331–352, https://doi.org/10.1016/j.jfranklin.2010.12.001, MR2771844, 2-s2.0-79251600177.
10.1016/j.jfranklin.2010.12.001
Web of Science® Google Scholar
19 Xiang W. and Xiao J., Stability analysis and control synthesis of switched impulsive systems, International Journal of Robust and Nonlinear Control. (2012) 22, no. 13, 1440–1459, https://doi.org/10.1002/rnc.1757, MR2956588, ZBL1287.93079, 2-s2.0-84864473393.
10.1002/rnc.1757
Web of Science® Google Scholar
20 Xiang W., Xiao J., and Iqbal M. N., Asymptotic stability, gain, boundness analysis, and control synthesis for switched systems: a switching frequency approach, International Journal of Adaptive Control and Signal Processing. (2012) 26, no. 4, 350–373, https://doi.org/10.1002/acs.1287, MR2913645, 2-s2.0-84859786253.
10.1002/acs.1287
Web of Science® Google Scholar
21 Xiang W., Xiao J., and Iqbal M. N., Robust observer design for nonlinear uncertain switched systems under asynchronous switching, Nonlinear Analysis: Hybrid Systems. (2012) 6, no. 1, 754–773, https://doi.org/10.1016/j.nahs.2011.08.001, MR2854912, 2-s2.0-80052535002.
10.1016/j.nahs.2011.08.001
Web of Science® Google Scholar
22 Zhao X., Zhang L., Shi P., and Liu M., Stability of switched positive linear systems with average dwell time switching, Automatica. (2012) 48, no. 6, 1132–1137, https://doi.org/10.1016/j.automatica.2012.03.008, MR2917523, 2-s2.0-84860315302.
10.1016/j.automatica.2012.03.008
Web of Science® Google Scholar
23 Zhao X., Liu X., Yin S., and Li H., Improved results on stability of continuous-time switched positive linear systems, Automatica. (2014) 50, no. 2, 614–621, https://doi.org/10.1016/j.automatica.2013.11.039, MR3163812.
10.1016/j.automatica.2013.11.039
Web of Science® Google Scholar
24 Zhao X., Yin S., Li H., and Niu B., Switching stabilization for a class of slowly switched systems, IEEE Transactions on Automatic Control. (2014) no. 99, 1, https://doi.org/10.1109/TAC.2014.2322961.
10.1109/TAC.2014.2322961
Google Scholar

Citing Literature

All articles

Positive Switched System Approach to Traffic Signal Control for Oversaturated Intersection

Abstract

1. Introduction

2. System Description and Problem Formulation

2.1. System Description and Modeling

2.2. Control Problem Formulation

3. Dissipativity Analysis for Positive Switched System

4. Control Solution for Two-Phase Intersection

5. Extension to Multiphase Intersection

6. Conclusions

Conflict of Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Positive Switched System Approach to Traffic Signal Control for Oversaturated Intersection

Abstract

1. Introduction

2. System Description and Problem Formulation

2.1. System Description and Modeling

2.2. Control Problem Formulation

3. Dissipativity Analysis for Positive Switched System

4. Control Solution for Two-Phase Intersection

5. Extension to Multiphase Intersection

6. Conclusions

Conflict of Interests

References

Citing Literature

Figures

References

Related

Information