We have presented a class of charged superdense star models, starting with a static spherically symmetric metric in isotropic coordinates for anisotropic fluid by considering Hajj-Boutros-(1986) type metric potential and a specific choice of electrical intensity E and anisotropy factor Δ which involve charge parameter K and anisotropy parameter α. The solution is well behaved for all the values of Schwarzschild compactness parameter u lying in the range 0 < u ≤ 0.2086, for all values of charge parameter K lying in the range 0.04 ≤ K ≤ 0.111 , and for all values of anisotropy parameter α lying in the range 0.016 ≥ α ≥ 0. With the increase in α, the values of K and u decrease. Further, we have constructed a superdense star model with all degree of suitability. The solution so obtained is utilized to construct the models for superdense star like neutron stars ρ_b = 2.7 × 10¹⁴ g/cm³ and strange quark stars ρ_b = 4.6888 × 10¹⁴ g/cm³ . For K = 0.06 and α = 0.01, the maximum mass of neutron star is observed as M = 1.53 M_⊙ and radius R = 11.48 km. Further for strange quark stars M = 1.16 M_⊙ and R = 8.71 km are obtained.

1. Introduction

Since the formulation of Einstein-Maxwell field equations, the relativists have been proposing different models of immensely gravitating astrophysical objects by considering the distinct nature of matter or radiation (energy-momentum tensor) present in them. Einstein-Maxwell field equations with anisotropic matter in isotropic coordinates have more importance over Einstein field equations for perfect fluid in curvature coordinates due to following rationale justifications.

(i)
The presence of some charge may avert the catastrophic gravitational collapse by counterbalancing the gravitational attraction by the electric repulsion in addition to the pressure gradient.
(ii)
The inclusion of charge inhibits the growth of space time curvature which has a great role in avoiding singularities (Ivanov [1]; de Felice et al. [2]).
(iii)
Bonnor [3] pointed out that a dust distribution of arbitrarily large mass and small radius can remain in equilibrium against the pull of gravity by a repulsive force produced by a small amount of charge.
(iv)
The solutions of Einstein-Maxwell equations are useful to study the cosmic matter.
(v)
The charge dust models and electromagnetic mass models are providing some clue about the structure of electron (Bijalwan [4]) and Lepton model (Kiess [5]).
(vi)
Several solutions which do not satisfy some or all the conditions for well-behaved nature can be renewed into well-behaved nature by charging them.
(vii)
Maharaj-Takisa [6] pointed out that the astrophysical objects have essential characteristics of rotational motion, which is caused by the presence of anisotropic parameter. Therefore, the matter in reality cannot be perfect fluid; Ruderman [7] and Sharma and Maharaj [8] also justified that the anisotropic always prevails in a certain density range ≈10¹⁵ g/cm³.
(viii)
Ivanov [9] pointed out that solutions in isotropic coordinates are more significant than the solutions in curvature coordinates, due to the following reasons: (a) the solutions in isotropic coordinates are simple in terms of algebraic expressions; (b) isotropic coordinates solutions can be used as seed solutions in Quasar modeling or nonstatic solutions.

Thus for realistic model it is desirable to study the insinuation of Einstein-Maxwell field equations with reference to the general relativistic prediction of gravitational collapse with anisotropic matter. For this purpose charged fluid ball models are required. The external field of such ball is to be matched with Reissner-Nordstrom solution. The solutions of Einstein-Maxwell field equations successfully explain the characteristics of massive objects like neutron star, quark star, or other superdense objects. Further, these stars are specified in terms of their masses and densities.

(a)
A neutron star has surface density ρ_b = 2.7 × 10¹⁴ g/cm³ (Astashenok [10]) and mass 1.4 M_⊙ − 2.9 M_⊙. However, Astashenok [10] established that f(R) models with realistic equation of state of neutron star have upper limit mass 2 M_⊙ and minimal radius close to 9 km.
(b)
A strange quark star has surface density ρ_b = 4.6888 × 10¹⁴ g/cm³ (Fatema and Murad [11]; Zdunik [12]) and possible maximum mass 2M_⊙. However, Dong et al. [13] established that due to presence of half skyrmions in the dense baryonic matter the stable strange quark star can have upper mass limit up to 2.4M_⊙.

In recent past, a considerable number of exact solutions with well-behaved nature of general relativistic field equation with anisotropic matter have been obtained; Dev and Gleiser [14], Komathiraj and Maharaj [15, 16], Thirukkanesh and Regel [17], Takisa and Maharaj [18, 19], Mak and Harko [20], Mak et al. [21], Ivanov [1], Maurya and Gupta [22, 23], Chaisi and Maharaj [24], and Feroze and Siddiqui [25] deal with curvature coordinates and some of them are charged models. By motivation of Maharaj-Takisa [6] and Ivanov [9], in this paper, we present a new class of well-behaved exact solutions of Einstein-Maxwell field equations in isotropic coordinates for anisotropic fluid assuming a particular form of one of the metric potentials and suitable choice of electric intensity and anisotropy.

2. Field Equations in Isotropic Coordinates

We consider the static and spherically symmetric metric in isotropic coordinates

()

where ω and ν are functions of r.

The Einstein-Maxwell field equations for a nonempty space-time are

()

where

is Ricci tensor,

is energy-momentum tensor, R is the scalar curvature, F_jm is the electromagnetic field tensor, p_r denotes the radial pressure, p_⊥ is the transversal pressure, ρ is the density distribution, χⁱ is the unit space-like vector in the radial direction, and vⁱ is the velocity vector, satisfying the relation

()

Since the field is static,

()

Thus we find that for the metric (1) under these conditions and for matter distributions with anisotropic pressure the field equation (2) reduces to the following:

()

where prime ( ^′) denotes differentiation with respect to r. From (5) and (6) we obtain the following differential equation in ω and υ:

()

Our task is to explore the solutions of (8) and to obtain the fluid parameters p_r, p_⊥, and ρ from (5), (6), and (7).

To solve the above equation we consider a seed solution as a particular case of Hajj-Boutros [26], Murad-Pant [27] and the electric intensity E of the following form:

()

where K is a positive constant defined as charge parameter. The electric intensity is so assumed that the model is physically significant and well behaved; that is, E remains regular and positive throughout the sphere. In addition, E vanishes at the center of the star and increases towards the boundary.

We also take

()

where “Δ” is the anisotropy factor whose value is zero at the center and increases towards the boundary and “α” is a positive constant defined as anisotropy parameter.

3. Conditions for Well-Behaved Solution

For well-behaved nature of the solution in isotropic coordinates, the following conditions should be satisfied (Mak and Harko [20] and Maurya and Gupta [22]).

(i)
The solution should be free from physical and geometrical singularities, that is, finite and positive values of central pressure, central density, and nonzero positive values of e^ω and e^υ.
(ii)
The radial pressure p_r must be vanishing, but the tangential pressure p_⊥ may not vanish at the boundary r = r_b of the sphere. However, the radial pressure is equal to the tangential pressure at the centre of the fluid sphere.
(iii)
The density ρ and pressures p_r, p_⊥ should be positive inside the star.
(iv)
and so that pressure gradient dp_r/dr is negative for 0 ≤ r ≤ r_b.
(v)
and so that pressure gradient dp_⊥/dr is negative for 0 ≤ r ≤ r_b.
(vi)
(dρ/dr)_r=0 = 0 and so that density gradient dρ/dr is negative for 0 ≤ r ≤ r_b.
Conditions (iv)–(vi) imply that pressure and density should be maximum at the centre and monotonically decreasing towards the surface.
(vii)
Inside the static configuration the casualty condition should be obeyed; that is, the speed of sound should be less than the speed of light; that is, and . In addition to the above the velocity of sound should be decreasing towards the surface; that is, (d/dr)(dp_r/dρ) < 0 or (d²p_r/dρ²) > 0 and (d/dr)(dp_⊥/dρ) < 0 or (d²p_⊥/dρ²) > 0 for 0 ≤ r ≤ r_b; that is, the velocity of sound is increasing with the increase of density. In this context it is worth mentioning that the equation of state at ultrahigh distribution has the property that the sound speed is decreasing outwards (Canuto and Lodenquai [28]).
(viii)
A physically reasonable energy-momentum tensor has to obey the conditions ρ ≥ p_r + 2p_⊥ and ρ + p_r + 2p_⊥ ≥ 0.
(ix)
The central red shift Z₀ and the surface red shift Z_b should be positive and finite; that is, and and both should be bounded.
(x)
Electric intensity E, such that E_r=0 = 0 and is taken to be monotonically increasing.
(xi)
The anisotropy factor Δ should be zero at the center and increasing towards the surface.

4. A New Class of Solutions

Equation (8) is solved by assuming the seed solution as a particular case of Hajj-Boutros [26], Murad-Pant [27] and the electric intensity E and the anisotropy factor Δ in such a manner that the solution can be obtained and physically viable. Thus we have

()

On substituting the above in (8), we get the following Riccati-differential equation in y:

()

which yields the following solution:

()

where A, B, C, and K are arbitrary constants and

()

where S is real for K + α ≥ 1/18.

The expressions for density, radial pressure, and transversal pressure are given by

()

where

()

5. Properties of the New Solution

The central values of pressure and density are given by

()

The central values of pressure and density will be nonzero positive definite if the following conditions are satisfied:

()

The pressure to density ratios are given by

()

Subjecting to the condition that the ratio of pressure to density should be positive and less than 1 at the centre, that is, p₀/ρ₀c² ≤ 1, the following inequality has to be satisfied.

()

All the values of A which satisfy (21) will also lead to the condition p₀/ρ₀c² ≤ 1.

Differentiating (16) with respect to r, we get

()

Thus it is found that maxima of p_r occur at the centre; that is,

()

Thus the expression of the right-hand side of (26) is negative for all values of A satisfying condition (21), showing thereby that the pressure (p_r) is maximum at the centre and monotonically decreasing.

Differentiating (17) with respect to r, we get

()

Thus it is found that maxima of p_⊥ occur at the centre; that is,

()

Thus the expression of the right-hand side of (28) is negative for all values of A satisfying condition (21), showing thereby that the transversal pressure is maximum at the centre and monotonically decreasing.

Now differentiating equation (15) with respect to r we get

()

Thus the maxima of ρ occur at the centre; that is,

()

Thus, the expression of the right-hand side of (30) is negative showing thereby that the density ρ is maximum at the centre and monotonically decreasing.

The square of adiabatic sound speed at the centre, (1/c²)(dp/dρ)_r=0, is given by

()

The causality condition is obeyed at the centre for all values of constants satisfying condition (21). Due to cumbersome expressions the trend of pressure-density ratios and adiabatic sound speeds are studied analytically after applying the boundary conditions.

6. Boundary Conditions in Isotropic Coordinates

For exploring the boundary conditions, we use the principle that the metric coefficients g_ij and their first derivatives g_ij,k in interior solution (I) as well as in exterior solution (E) are continuous up to and on the boundary B. The continuity of metric coefficients g_ij of I and B on the boundary is the known first fundamental form. The continuity of derivatives of metric coefficients g_ij of I and B on the boundary is the known second fundamental form.

The exterior field of a spherically symmetric static charged fluid distribution is described by Reissner-Nordstrom metric given by

()

where M is the mass of the ball as determined by the external observer and R is the radial coordinate of the exterior region.

Since Reissner-Nordstrom metric (33) is considered as the exterior solution, we will arrive at the following conclusions by matching first and second fundamental forms:

()

Equations (34) to (37) are four conditions, known as boundary conditions in isotropic coordinates. Moreover (35) and (37) are equivalent to zero pressure of the interior solution on the boundary.

Applying the boundary conditions from (34) to (37), we get the values of the arbitrary constants in terms of Reissner-Nordstrom parameter “d,” Schwarzschild parameters u = GM/c²R_b, and radius of the star R_b;

()

where we define a new parameter called Reissner-Nordstrom parameter “d” given by

()

whose value lies within 2/3 < d < 1 for

Surface density is given by

()

Central red shift is given by

()

The surface red shift is given by

()

7. Discussions and Conclusions

From Figures 1 and 2 it has been observed that the physical quantities p_r, p_⊥, p_r/ρc², p_⊥/ρc², dp_r/c²dρ, dp_⊥/c²dρ, and z are positive at the centre and within the limit of realistic state equation and monotonically decreasing while the quantities γ, Δ, E are increasing for all values of K, α, and u lying in the ranges 0.04 ≤ K ≤ 0.111, 0 < α ≤ 0.016, and 0 ≤ u ≤ 0.2086, respectively. For K + α > 0.111 the pressure is negative. With the increase in the value of K from 0.04 to 0.111 the Schwarzschild parameter “u” increases; hence the mass increases, but the value of α has to be decreased to 0. With α = 0 we recover the isotropic model.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The variation of p, ρ, p/ρc², Z, γ, and E from centre to surface for K = 0.06 and α = 0.01.

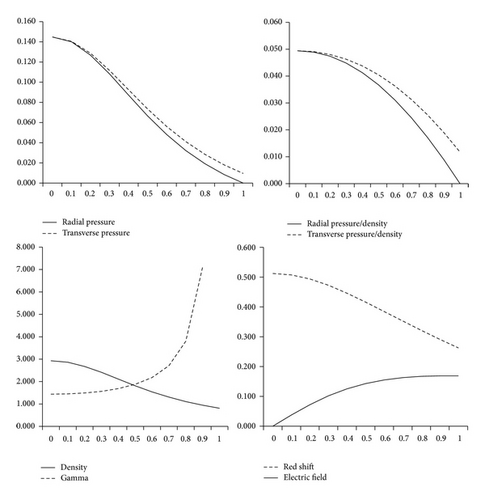
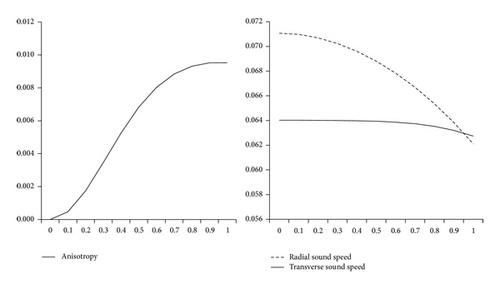
By increasing K above 0.111 the causality condition is obeyed throughout within the ball, but the trend of adiabatic sound speed (transversal) is erratic. Thus, the solution is well behaved for all values of u satisfying the inequality 0 ≤ u ≤ 0.2086 for K up to 0.111 and for α up to 0.016. From Figure 3 it is clearly shown that the mass of the superdense star has a linear dependence on its radius.

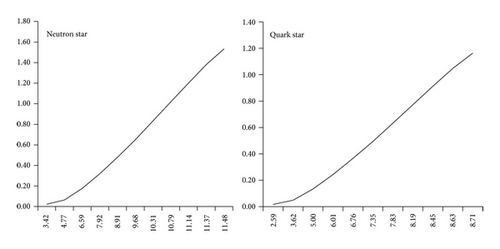
In Tables 1 and 2 we present a model of superdense neutron star and quark star based on the particular solution discussed above. By assuming surface density, ρ_b = 4.6888 × 10¹⁴ g/cm³ corresponding to α = 0.01, K = 0.06 for which u = 0.198, the resulting well-behaved solution has a maximum mass M = 1.16 M_⊙ and radius R = 8.71 km (for quark star) and by assuming the surface density ρ_b = 2.7 × 10¹⁴ g/cm³ the obtained maximum mass is M = 1.53 M_⊙ and radius R = 11.48 (for neutron star).

Table 1. Variation of maximum mass of neutron star and corresponding radius R_b with u for K = 0.06 and α = 0.01 by assuming the surface density ρ_b = 2.7 × 10¹⁴ g/cm³.

u		R_b (km)	M/M_⊙
0.010	0.08605	3.41575	0.02299
0.020	0.16661	4.77451	0.06413
0.040	0.31173	6.59067	0.17622
0.060	0.44198	7.92405	0.32153
0.080	0.54874	8.91444	0.48155
0.100	0.63497	9.68137	0.65060
0.120	0.70596	10.31179	0.83478
0.140	0.75730	10.78723	1.01872
0.160	0.79117	11.13602	1.20163
0.180	0.80834	11.36756	1.38018
0.198	0.81007	11.47792	1.53364

Table 2. Showing the variation of maximum mass of Quark star (ρ_b = 4.6888 × 10¹⁴ g/cm³), its radius, surface red shift, surface electric intensity, and surface anisotropy with u for K = 0.06 and α = 0.01.

u	R_B (km)	M/M_⊙	Z_b	E_br_b
0.010	2.59201	0.01745	0.010101	0.008901	0.000026
0.020	3.62309	0.04866	0.020408	0.017722	0.000105
0.040	5.00127	0.13373	0.041667	0.035122	0.000411
0.060	6.01310	0.24399	0.064963	0.053045	0.000938
0.080	6.76465	0.36542	0.088850	0.070282	0.001646
0.100	7.34663	0.49370	0.113586	0.087017	0.002524
0.120	7.82502	0.63347	0.140901	0.104300	0.003626
0.140	8.18579	0.77305	0.169317	0.121076	0.004886
0.160	8.45047	0.91185	0.199472	0.137677	0.006318
0.180	8.62618	1.04734	0.231679	0.154199	0.007926
0.198	8.70992	1.16379	0.262626	0.169054	0.009526

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

The authors acknowledge their gratitude to Major General Ashok Ambre, SM, Deputy Commandant, NDA, for his motivation and encouragement. They also extend their gratitude to Professor O. P. Shukla, Principal, NDA, for his encouragement. They are grateful to the anonymous referees for their rigorous review, constructive comments, and useful suggestions.

References

1 Ivanov B. V., Static charged perfect fluid spheres in general relativity, Physical Review D. (2002) 65, no. 10, 17, 104001, https://doi.org/10.1103/PhysRevD.65.104001, MR1918996.
10.1103/PhysRevD.65.104001
CAS Web of Science® Google Scholar
2 de Felice F., Yu Y., and Fang J., Relativistic charged spheres, Monthly Notices of the Royal Astronomical Society. (1995) 277.
Web of Science® Google Scholar
3 Bonnor W. B., The equilibrium of charged sphere, Monthly Notices of the Royal Astronomical Society. (1965) 137, no. 3, 239–251.
10.1093/mnras/137.3.239
Google Scholar
4 Bijalwan N., Exact solutions: classical electron model, Astrophysics and Space Science. (2011) 336, no. 2, 485–489, https://doi.org/10.1007/s10509-011-0796-5, 2-s2.0-81855198956.
10.1007/s10509-011-0796-5
Web of Science® Google Scholar
5 Kiess T. E., A nonsingular perfect fluid classical lepton model of arbitrarily small radius, International Journal of Modern Physics D. (2013) 22, 1350088.
10.1142/S0218271813500880
Web of Science® Google Scholar
6 Maharaj S. D. and Takisa P. M., Regular models with quadratic equation of state, General Relativity and Gravitation. (2012) 44, no. 6, 1419–1432, https://doi.org/10.1007/s10714-012-1347-2, 2-s2.0-84861231596.
10.1007/s10714-012-1347-2
Web of Science® Google Scholar
7 Ruderman R., Pulsars: structure and dynamics, Annual Review of Astronomy and Astrophysics. (1972) 10, 427–476, https://doi.org/10.1146/annurev.aa.10.090172.002235.
10.1146/annurev.aa.10.090172.002235
Web of Science® Google Scholar
8 Sharma R. and Maharaj S. D., A class of relativistic stars with a linear equation of state, Monthly Notices of the Royal Astronomical Society. (2007) 375, 1265–1268, https://doi.org/10.1111/j.1365-2966.2006.11355.x.
10.1111/j.1365-2966.2006.11355.x
Web of Science® Google Scholar
9 Ivanov B. V., Collapsing shear-free perfect fluid spheres with heat flow, General Relativity and Gravitation. (2012) 44, no. 7, 1835–1855, https://doi.org/10.1007/s10714-012-1370-3, MR2935208, ZBL1246.83154.
10.1007/s10714-012-1370-3
Web of Science® Google Scholar
10 Astashenok A. V., Capozziello S., and Odintsov S. D., Further stable neutron star models from f(R) gravity, 2013, http://arxiv.org/abs/1309.1978.
Google Scholar
11 Fatema S. and Murad M. H., An exact family of Einstein-Maxwell Wyman-Adler solution in general relativity, International Journal of Theoretical Physics. (2013) 52, no. 7, 2508–2529.
10.1007/s10773-013-1538-y
Web of Science® Google Scholar
12 Zdunik J. L., Strange stars—linear approximation of the EOS and maximum QPO frequenc, Astronomy & Astrophysics. (2000) 359, 311–315.
Web of Science® Google Scholar
13 Dong H., Kuo T. T. S., Lee H. K., Machleidt R., and Rho M., Half-Skyrmions and the equation of state for compact-star matter, Physical Review C. (2013) 87, 054332, https://doi.org/10.1103/PhysRevC.87.054332.
10.1103/PhysRevC.87.054332
Web of Science® Google Scholar
14 Dev K. and Gleiser M., Anisotropic stars: exact solutions, General Relativity and Gravitation. (2002) 34, no. 11, 1793–1818, https://doi.org/10.1023/A:1020707906543, MR1945325, ZBL1014.83015, 2-s2.0-0141453233.
10.1023/A:1020707906543
Web of Science® Google Scholar
15 Komathiraj K. and Maharaj S. D., Tikekar superdense stars in electric fields, Journal of Mathematical Physics. (2007) 48, 12, 042501, https://doi.org/10.1063/1.2716204, MR2319886.
10.1063/1.2716204
CAS Web of Science® Google Scholar
16 Komathiraj K. and Maharaj S. D., Analytical models for quark stars, International Journal of Modern Physics D. (2007) 16, no. 11, 1803–1811, https://doi.org/10.1142/S0218271807011103, MR2371532, 2-s2.0-36849006944.
10.1142/S0218271807011103
CAS Web of Science® Google Scholar
17 Thirukkanesh S. and Ragel F. C., Exact anisotropic sphere with polytropic equation of state, Pramana. (2012) 78, no. 5, 687–696, https://doi.org/10.1007/s12043-012-0268-7, 2-s2.0-84861498871.
10.1007/s12043-012-0268-7
Web of Science® Google Scholar
18 Takisa P. M. and Maharaj S. D., Compact models with regular charge distributions, Astrophysics and Space Science. (2013) 343, no. 2, 569–577, https://doi.org/10.1007/s10509-012-1271-7, 2-s2.0-84871927528.
10.1007/s10509-012-1271-7
Web of Science® Google Scholar
19 Takisa P. M. and Maharaj S. D., Some charged polytropic models, General Relativity and Gravitation. (2013) 45, no. 10, 1951–1969, https://doi.org/10.1007/s10714-013-1570-5, MR3103957, ZBL1277.83032, 2-s2.0-84883134839.
10.1007/s10714-013-1570-5
Web of Science® Google Scholar
20 Mak M. K. and Harko T., An exact anisotropic quark star model, Chinese Journal of Astronomy and Astrophysics. (2002) 2, no. 3, 248–260, https://doi.org/10.1088/1009-9271/2/3/248.
10.1088/1009-9271/2/3/248
CAS Web of Science® Google Scholar
21 Mak M. K., Dobson P. N., and Harko T., Exact model for anisotropic relativistic stars, International Journal of Modern Physics D. (2002) 11, 207–221.
10.1142/S0218271802001317
CAS Web of Science® Google Scholar
22 Maurya S. K. and Gupta Y. K., A family of anisotropic super-dense star models using a space-time describing charged perfect fluid distributions, Physica Scripta. (2012) 86, 025009, https://doi.org/10.1088/0031-8949/86/02/025009.
10.1088/0031-8949/86/02/025009
Web of Science® Google Scholar
23 Maurya S. K. and Gupta Y. K., Charged fluid to anisotropic fluid distribution in general relativity, Astrophysics and Space Science. (2013) 344, no. 1, 243–251, https://doi.org/10.1007/s10509-012-1302-4, ZBL1276.85010, 2-s2.0-84873992089.
10.1007/s10509-012-1302-4
Web of Science® Google Scholar
24 Chaisi M. and Maharaj S. D., Anisotropic static solutions in modelling highly compact bodies, Journal of Physics. (2006) 66, no. 3, 609–614, https://doi.org/10.1007/BF02704504, 2-s2.0-33645052999.
10.1007/BF02704504
Google Scholar
25 Feroze T. and Siddiqui A. A., Charged anisotropic matter with quadratic equation of state, General Relativity and Gravitation. (2011) 43, no. 4, 1025–1035, https://doi.org/10.1007/s10714-010-1121-2, MR2785370, ZBL1216.83031, 2-s2.0-79953062532.
10.1007/s10714-010-1121-2
Web of Science® Google Scholar
26 Hajj-Boutros J., Spherically symmetric perfect fluid solutions in isotropic coordinates, Journal of Mathematical Physics. (1986) 27, no. 5, 1363–1366, https://doi.org/10.1063/1.527091, MR836038, ZBL0594.76126, 2-s2.0-0345756559.
10.1063/1.527091
Web of Science® Google Scholar
27 Murad H. M. and Pant N., A class of exact isotropic solutions of Einstein’s equations and relativistic stellar models in general relativity, Astrophysics and Space Science. (2014) 350, no. 1, 349–359, https://doi.org/10.1007/s10509-013-1713-x.
10.1007/s10509-013-1713-x
Web of Science® Google Scholar
28 Canuto V. and Lodenquai J., Solidification of neutron matter, Physical Review C. (1975) 12, no. 6, 2033–2037, https://doi.org/10.1103/PhysRevC.12.2033, 2-s2.0-35949044944.
10.1103/PhysRevC.12.2033
CAS Web of Science® Google Scholar

Citing Literature

All articles

Anisotropic Charged Fluid Sphere in Isotropic Coordinates

Abstract

1. Introduction

2. Field Equations in Isotropic Coordinates

3. Conditions for Well-Behaved Solution

4. A New Class of Solutions

5. Properties of the New Solution

6. Boundary Conditions in Isotropic Coordinates

7. Discussions and Conclusions

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Anisotropic Charged Fluid Sphere in Isotropic Coordinates

Abstract

1. Introduction

2. Field Equations in Isotropic Coordinates

3. Conditions for Well-Behaved Solution

4. A New Class of Solutions

5. Properties of the New Solution

6. Boundary Conditions in Isotropic Coordinates

7. Discussions and Conclusions

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Related

Information