Discrete Dynamics in Nature and Society
Volume 2014, Issue 1 365981
Research Article
Open Access

Local Fractional Laplace Variational Iteration Method for Solving Linear Partial Differential Equations with Local Fractional Derivative

Ai-Min Yang, 

Ai-Min Yang

College of Science, Hebei United University, Tangshan 063009, China hebeiuniteduniversity.com

College of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China ysu.edu.cn

Search for more papers by this author
Jie Li, 

Jie Li

College of Science, Hebei United University, Tangshan 063009, China hebeiuniteduniversity.com

School of Materials and Metallurgy, Northeast University, Shenyang 110819, China neu.edu.cn

Search for more papers by this author
H. M. Srivastava, 

H. M. Srivastava

Department of Mathematics and Statistics, University of Victoria, Victoria, BC, Canada V8W 3R4, uvic.ca

Search for more papers by this author
Gong-Nan Xie, 

Gong-Nan Xie

School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an, Shaanxi 710048, China npu.edu

Search for more papers by this author
Xiao-Jun Yang, 

Corresponding Author

Xiao-Jun Yang

Department of Mathematics and Mechanics, China University of Mining and Technology, Xuzhou, Jiangsu 221008, China cumtb.edu.cn

Search for more papers by this author
First published: 17 July 2014
https://doi.org/10.1155/2014/365981
Citations: 12
Academic Editor: Bing Xu

Abstract

The local fractional Laplace variational iteration method was applied to solve the linear local fractional partial differential equations. The local fractional Laplace variational iteration method is coupled by the local fractional variational iteration method and Laplace transform. The nondifferentiable approximate solutions are obtained and their graphs are also shown.

1. Introduction

Fractional calculus [1] has successfully been used to study the mathematical and physical problems arising in science and engineering. Fractional differential equations are applied to describe the dynamical systems in physics and engineering (see [2, 3]). It is one of the hot topics for finding the solutions for the fractional differential equations for scientists and engineers. There are many analytical and numerical methods for solving them, such as the spectral Legendre-Gauss-Lobatto collocation method [4], the shifted Jacobi-Gauss-Lobatto collocation method [5], the variation iteration method [6], the heat-balance integral method [7], the Adomian decomposition method [8], the finite element method [9], and the finite difference method [10].

The above methods did not deal with some nondifferentiable problems arising in mathematics and physics (see [11–13]). Local fractional calculus (see [12–14] and the cited references) is the best choice to deal with them. Some methods for solving the local fractional differential equations were suggested, such as the Cantor-type cylindrical-coordinate method [15], the local fractional variational iteration method [16, 17], the local fractional decomposition method [18], the local fractional series expansion method [19], the local fractional Laplace transform method [20], and local fractional function decomposition method [21, 22]. More recently, the coupling schemes for local fractional variational iteration method and Laplace transform were suggested in [23]. However, the results are very little. In this paper, our aim is to use the local fractional Laplace variational iteration method to solve the linear local fractional partial differential equations. The structure of the paper is suggested as follows. In Section 2 the basic theory of local fractional calculus and local fractional Laplace transform are introduced. Section 3 is devoted to the local fractional Laplace variational iteration method. In Section 4, the four examples for the local fractional partial differential equations are given. Finally, the conclusions are considered in Section 5.

2. Local Fractional Calculus and Local Fractional Laplace Transform

In this section, we present the basic theory of local fractional calculus and concepts of local fractional Laplace transform.

The local fractional derivative of f(x) of order α is defined as [12–15]
(1)
where
(2)
The local fractional integral of f(x) of order α in the interval [a, b] is defined as [12–14, 16–23]
(3)
where the partitions of the interval [a, b] are (tj, tj+1), with Δtj = tj+1 − tj, t0 = a, tN = b, and Δt = max⁡{Δt0, Δt1, Δtj, …}, j = 0, …, N − 1.
The local fractional series of nondifferentiable function used in this paper are presented as follows [12–14]:
(4)
The properties of local fractional derivatives and integral of nondifferentiable functions are given by [12, 13]
(5)
The local fractional Laplace transform is defined as [12, 20–22]
(6)
where f(x) is local fractional continuous and sα = βα + iα∞α.
The inverse formula of local fractional Laplace transform is defined as [12, 20–22]
(7)
where sα = βα + iα∞α and Re(sα) = βα.
The local fractional convolution of two functions is defined as [12, 20–22]
(8)
The properties for local fractional Laplace transform used in the paper are given as [12]
(9)

3. Analysis of the Method

In this section, we introduce the idea of local fractional variational iteration method [16, 17], which is coupled by the local fractional variational iteration method and Laplace transform.

Let us consider the following nonlinear operator with local fractional derivative:
(10)
where the linear local fractional differential operator denotes Lα = (dkα/dskα) and u(x) is a source term of the nondifferential function.
Following the local fractional Laplace variational iteration method [23], we have the local fractional functional formula as follows:
(11)
which leads to
(12)
Using the local fractional Laplace transform, from (12), we get
(13)
Taking the local fractional variation [21], we obtain
(14)
which leads to
(15)
where
(16)
Hence, from (15) and (16) we get
(17)
which yields
(18)
Hence, we get the new iteration algorithm as follows:
(19)
where the initial value is suggested as
(20)
Therefore, we have the local fractional series solution of (10)
(21)
so that
(22)
The above process is called the local fractional variational iteration method.

4. The Nondifferentiable Solutions for Linear Local Fractional Differential Equations

In this section, we present the examples for linear local fractional differential equations of high order.

Example 1. The local fractional differential equation is presented as

(23)
subject to the initial value
(24)
From (19) and (23) we obtain
(25)
where the initial value is given by
(26)
Therefore, the successive approximations are
(27)
Hence, we get
(28)
and its graph is shown in Figure 1.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Plot of u(x, t) with the fractal dimension α = ln⁡⁡2/ln⁡⁡3.

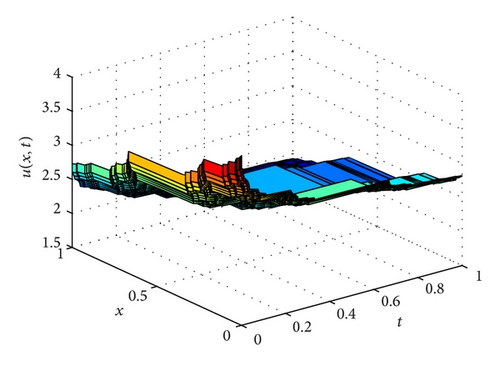
Example 2. We report the following local fractional partial differential equation:

(29)
The initial value is given by
(30)
In view of (19) and (29) the local fractional iteration algorithm can be written as follows:
(31)
where the initial value is
(32)
Making use of (31) and (32), the successive approximate solutions are shown as follows:
(33)
Therefore, the nondifferentiable solution of (29) reads
(34)
and its plot is presented in Figure 2.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Plot of u(x, t) with the parameters α = ln⁡⁡2/ln⁡⁡3 and k = 50.

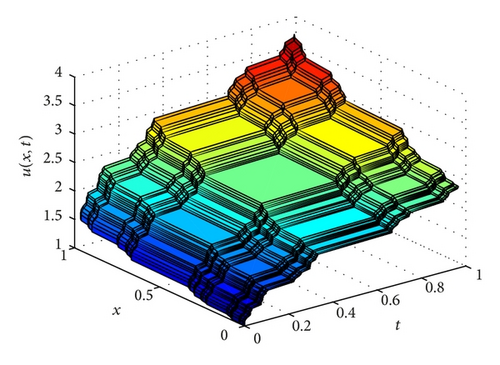
Example 3. The following local fractional partial differential equation

(35)
is considered and its initial value is
(36)
Making use of (19) and (35) the local fractional iteration algorithm reads
(37)
where the initial value is suggested as
(38)
From (38) we have the successive approximations as follows:
(39)
Hence, the approximate solution of (35) is given by
(40)
and its graph is presented in Figure 3.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Plot of u(x, t) with the parameters α = ln⁡⁡2/ln⁡⁡3 and k = 50.

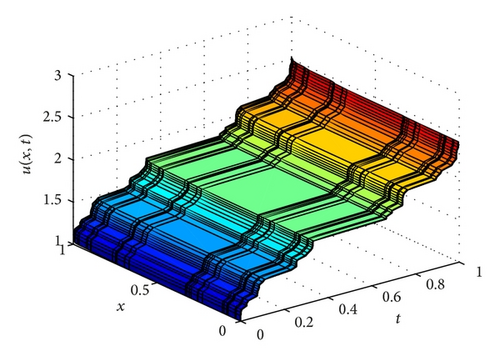
5. Conclusions

Local fractional calculus was successfully applied to deal with the nondifferentiable problems arising in mathematical physics. In this work we considered the coupling method of the local fractional variational iteration method and Laplace transform to solve the linear local fractional partial differential equations and their nondifferentiable solutions were obtained. The results are efficient implement of the local fractional Laplace variational iteration method to solve the partial differential equations with local fractional derivative.

Conflict of Interests

The authors declare that they have no competing interests in this paper.

Acknowledgments

This work was supported by National Scientific and Technological Support Projects (no. 2012BAE09B00), the National Natural Science Foundation of China (no. 51274270), and the National Natural Science Foundation of Hebei Province (no. E2013209215).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.