Advances in Statistics
Volume 2014, Issue 1 304724
Research Article
Open Access

Statistical Analysis of a Weibull Extension with Bathtub-Shaped Failure Rate Function

Ronghua Wang, 

Ronghua Wang

College of Mathematics and Science, Shanghai Normal University, Shanghai 200234, China shnu.edu.cn

Search for more papers by this author
Naijun Sha, 

Corresponding Author

Naijun Sha

Department of Mathematical Sciences, University of Texas at El Paso, El Paso, TX 79968, USA utep.edu

Search for more papers by this author
Beiqing Gu, 

Beiqing Gu

Business Information Management School, Shanghai University of International Business and Economics, Shanghai 201620, China suibe.edu.cn

Search for more papers by this author
Xiaoling Xu, 

Xiaoling Xu

Business Information Management School, Shanghai University of International Business and Economics, Shanghai 201620, China suibe.edu.cn

Search for more papers by this author
First published: 27 October 2014
https://doi.org/10.1155/2014/304724
Citations: 8
Academic Editor: Karthik Devarajan

Abstract

We consider the parameter inference for a two-parameter life distribution with bathtub-shaped or increasing failure rate function. We present the point and interval estimations for the parameter of interest based on type-II censored samples. Through intensive Monte-Carlo simulations, we assess the performance of the proposed estimation methods by a comparison of precision. Example applications are demonstrated for the efficiency of the methods.

1. Introduction

In reliability analysis, the failure rate function plays an essential role to characterize life phenomena. The failure pattern of many products/systems (as electronic and mechanical products, etc.) can be represented by a bathtub curve. It comprises three stages: initial stage (or burn-in) with a decreasing failure rate, middle stage with an approximately constant failure rate, and final stage with an increasing failure rate. Many probability distributions have been proposed to fit real life data with bathtub-shaped failure rates (e.g., [1–5]). Chen [6] proposed a two-parameter lifetime distribution (written as CZM(β, θ) throughout this paper) with bathtub failure rate whose distribution function is
()
where β > 0 is the shape parameter and θ > 0 the scale parameter. Obviously, the transformed random variable follows the standard exponential distribution Exp (1). Also note that for small x, and so the distribution CZM(β, θ), to some degree, can be treated as an extension of Weibull distribution.

In reliability engineering, two common censoring mechanisms are widely applied in reliability testing for product life. For type-I censoring, the test is continued until a prespecified time is reached; whereas for type-II censoring, the test is carried out until a preset number r of units failed. A significant amount of literature has emerged on various testing models with both data censoring schemes. Cha [7] considered a problem of determining optimal burn-in time in a bathtub-shaped failure model under both cases of type-I and type-II. Xiong [8] made a statistical inference on a step-stress model with type-II censored exponential data. Balakrishnan et al. [9] presented the order restricted MLE for multiple step-stress models with exponential lifetime under type-I and type-II censored sampling situations. A comparison of accelerated life testing for Weibull and lognormal distributions with type-II censoring was made by meeker [10], just to name a few.

Particularly, for the CZM(β, θ) distribution, there were some works done for parameter inference. Chen [6] presented the exact confidence intervals for the parameters based on type-II censored samples and gave an outline of the maximum likelihood estimation (MLE) procedure. Wu et al. [11] discussed the optimal pivotal quantities to provide a shortest exact confidence interval of the parameters and presented an alternate approximated one. Tang et al. [12] extended CZM(β, θ) to a three-parameter distribution, for which they studied the properties of the order statistics, and introduced the MLE estimation and likelihood ratio test. However, in general, this distribution has not been much explored for its characteristics and parameter inference.

In this paper, we will explore some features of CZM(β, θ) and primarily focus on the parameter inference. In Section 2, we first study the numerical and graphic characteristics of this distribution and correct some mistakes which appeared in Chen [6] and Tang et al. [12]. We present several methods of point and interval estimation for the parameters in Section 3. In Section 4 we assess the performance of the methods by comparing the estimation precision on simulation studies, followed by data examples in Section 5. Lastly we conclude the paper with a brief discussion in Section 6.

2. Characteristics of Distribution CZM(β, θ)

The density function for the distribution in (1) is
()
which has some interesting characteristics illustrated in Lemma 1.

Lemma 1. The density function f(x) has the following characteristics. (1) When β = 1, f(x) is decreasing for 0 < θ ≤ 1, and unimodal for θ > 1. (2) When β > 1, f(x) is unimodal. (3) When 0 < β < 1, (i) f(x) is decreasing for 0 < θ ≤ 1; (ii) if θ > 1, then f(x) is either decreasing, or first decreasing, then increasing and finally decreasing again.

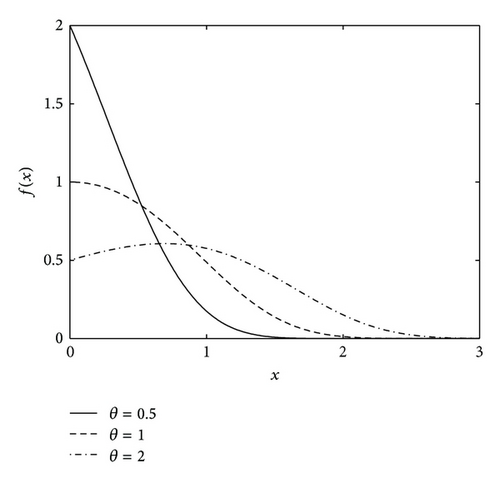
We provide a detail proof in the Appendix. Note that Lemma 1 corrects the wrong conclusion of Tang et al. [12], who claimed that the density f(x) was decreasing with β = 1, θ > 1. Figure 1 shows the density curves under various settings of parameter values. It is also worth noting that when β = 1, the distribution becomes an extreme value distribution, and when θ = 1, it reduces to an exponential power life distribution introduced by Dhillon [13], which can have increasing, decreasing, and bathtub-shaped failure rates. Hence, it seems that the distribution is flexible enough to model various situations of product life.

Details are in the caption following the image
Figure 1 (a) β = 1
Open in figure viewerPowerPoint
Density function f(x).
Details are in the caption following the image
Figure 1 (b) θ = 1,   β > 1
Open in figure viewerPowerPoint
Density function f(x).
Details are in the caption following the image
Figure 1 (c) θ = 1,   0 < β < 1
Open in figure viewerPowerPoint
Density function f(x).
Details are in the caption following the image
Figure 1 (d) θ = 10,   0 < β < 1
Open in figure viewerPowerPoint
Density function f(x).

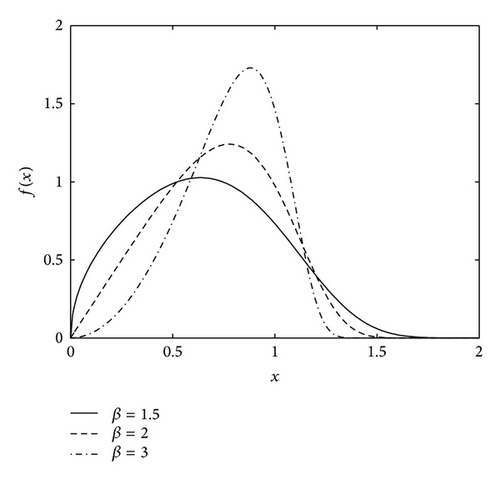
The failure rate function is , and , x > 0, thus λ(x) has a bathtub-shaped with achieving a minimum value at x = ((1 − β)/β)1/β when 0 < β < 1, and is increasing when β ≥ 1. Figure 2 illustrates λ(x) with various values of β and θ. Since the bottom of bathtub is the steady stage of failure rate function, it corresponds to the regular working stage of products and is very important for the practical application. To describe the length of time for working stage, we first give the definition of bathtub bottom width in the following.

Details are in the caption following the image
Figure 2 (a) θ = 1,   β ≥ 1
Open in figure viewerPowerPoint
Failure rate function λ(x).
Details are in the caption following the image
Figure 2 (b) θ = 1,   0 < β < 1
Open in figure viewerPowerPoint
Failure rate function λ(x).

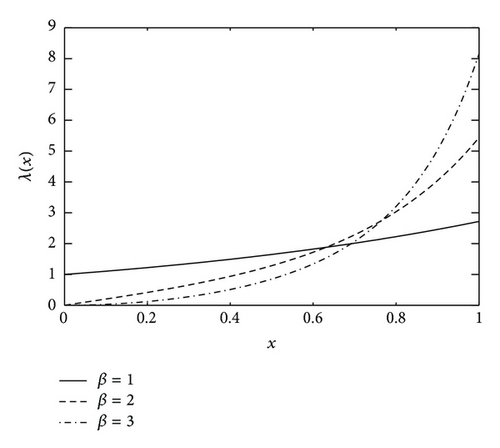
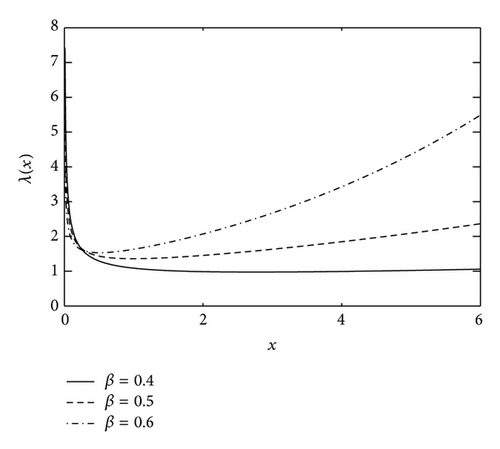
Definition 2. Suppose that a random variable X follows a bathtub-shaped failure rate function λ(x) with achieving the minimum at x0. For a given (bathtub height) ɛ > 0 and two roots x1, x2 of the equation λ(x) − λ(x0) = ɛ with x1 < x0 < x2, define the difference l(ɛ) = x2 − x1 as the bathtub bottom width of the given precision ɛ.

For CZM(β, θ) distribution, we have the following property of the bottom width for the failure rate function.

Theorem 3. For CZM(β, θ) with 0 < β < 1 and the bathtub-shaped failure rate function λ(x), then given ɛ > 0, the bathtub bottom width l(ɛ) is increasing for θ.

Proof. Since λ(x) has a bathtub-shaped for 0 < β < 1, given ɛ > 0, there are two roots x1 < x2 of the equation λ(x) − λ(x0) = ɛ with x0 = ((1 − β)/β)1/β. Taking derivative of the equation λ(x) − λ(x0) = ɛ with respect to θ, we have . Let , obviously g(x1) < 0 < g(x2) since x1 < x0 < x2. Thus, we obtain ∂l(ɛ)/∂θ = ∂(x2 − x1)/∂θ = (ɛ/β)[g(x2) − g(x1)] > 0. The theorem follows.

Given ɛ = 0.1,0.01,0.001,0.0001, and under various values of distribution parameters, the results of the bottom width are listed in Table 1, in which one can see that the width l(ɛ) is increasing for θ, on the contrary, l(ɛ) is decreasing for β.

Table 1. The bathtub bottom width.
β = 0.5 θ = 0.5
ε θ x1 x2 l(ε) = x2 − x1 β x1 x2 l(ε) = x2 − x1
0.1 0.5 0.5696 1.6729 1.1033 0.3 5.7180 44.6868 38.9688
1 0.4475 2.0322 1.5847 0.5 0.5696 1.6729 1.1033
2 0.3172 2.6219 2.3047 0.8 0.0867 0.3216 0.2349
  
0.01 0.5 0.8404 1.1841 0.3437 0.3 12.0165 23.3669 11.3504
1 0.7810 1.2679 0.4869 0.5 0.8404 1.1841 0.3437
2 0.7034 1.3943 0.6909 0.8 0.1428 0.2163 0.0734
  
0.001 0.5 0.9470 1.0555 0.1085 0.3 15.1556 18.7121 3.5565
1 0.9257 1.0792 0.1535 0.5 0.9470 1.0555 0.1085
2 0.8963 1.1135 0.2171 0.8 0.1655 0.1887 0.0232
  
0.0001 0.5 0.9830 1.0173 0.0343 0.3 16.2962 17.4198 1.1236
1 0.9760 1.0245 0.0485 0.5 0.9830 1.0173 0.0343
2 0.9662 1.0348 0.0686 0.8 0.1731 0.1805 0.0073

For the purpose of estimation, we explore other characteristics of the distribution including finite moments. Finite moments guarantee the rationality for the moment-based estimation methods such as method of moments. We display our findings for the properties of CZM(β, θ) shown in Theorem 4 whose proof is provided in the Appendix.

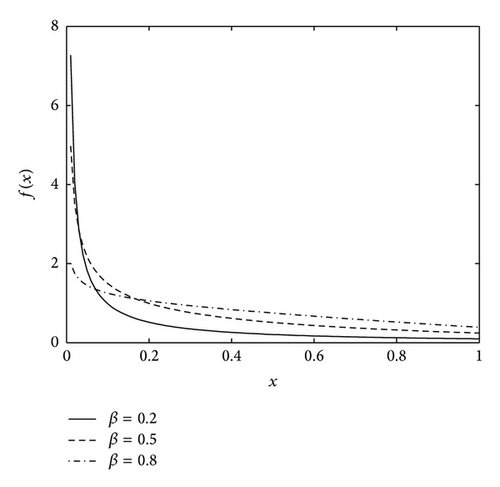
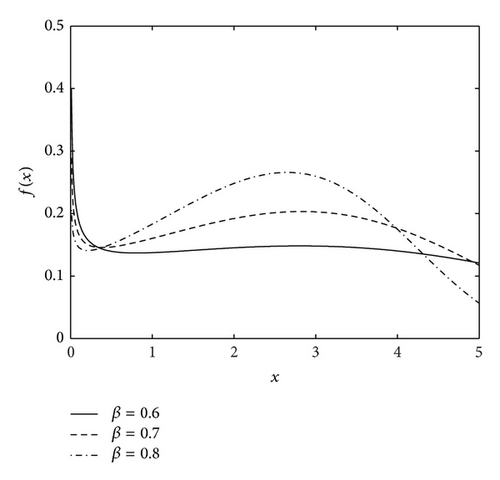
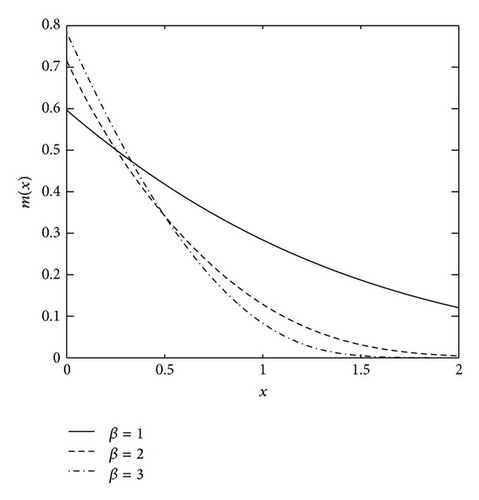
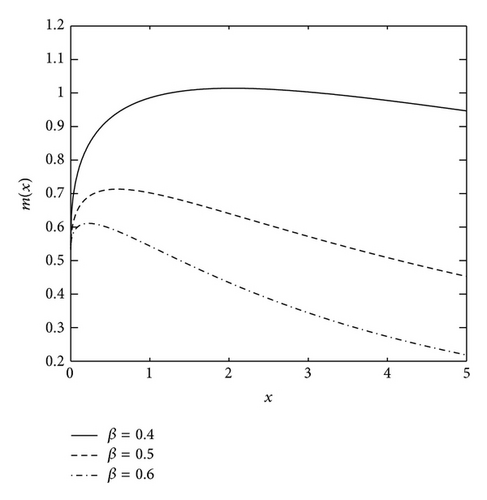
Theorem 4. Suppose X ~ CZM(β, θ). Then, (1) the moments exist; (2) the average failure rate G(x) = −(log⁡⁡(1 − F(x)))/x,  x > 0 is increasing for β ≥ 1 and has a bathtub-shaped (concave-up) for 0 < β < 1; (3) the average remaining lifetime function , x > 0 is decreasing for β ≥ 1, and unimodal for 0 < β < 1.

Not surprisingly, there is a similar characteristic for the failure rate λ(x) and average failure rate G(x). Figures 3 and 4 illustrate the shapes of G(x) and m(x) with various values of β.

Details are in the caption following the image
Figure 3 (a) θ = 1,   β ≥ 1
Open in figure viewerPowerPoint
Average failure function G(x).
Details are in the caption following the image
Figure 3 (b) θ = 1,   0 < β < 1
Open in figure viewerPowerPoint
Average failure function G(x).
Details are in the caption following the image
Figure 4 (a) θ = 1,   β ≥ 1
Open in figure viewerPowerPoint
Average remaining lifetime function m(x).
Details are in the caption following the image
Figure 4 (b) θ = 1,   0 < β < 1
Open in figure viewerPowerPoint
Average remaining lifetime function m(x).

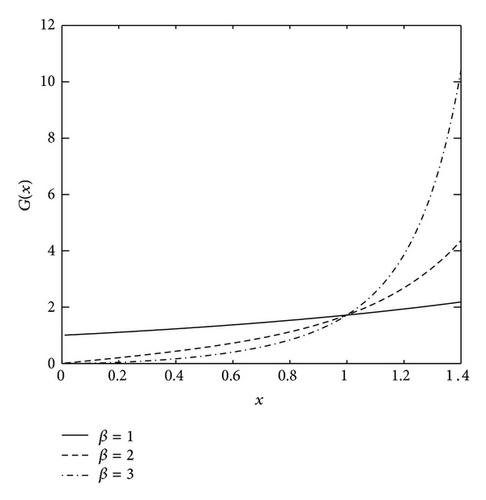
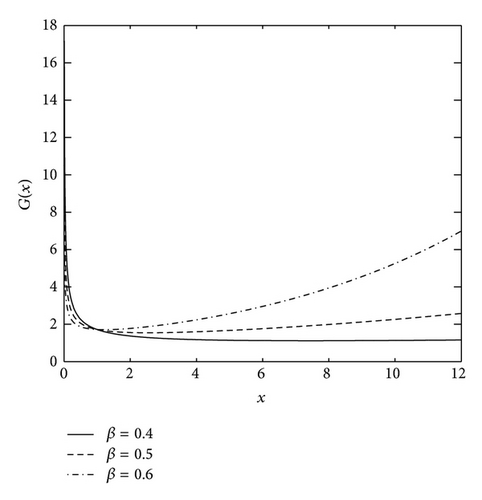
3. Estimation Methods

In this section, we discuss the estimation of parameters under type-II censored observational data. Suppose that n products whose lifetime follow CZM(β, θ) are placed on test and the test continues until predetermined r products fail with the ordered failure times x(1) ≤ x(2) ≤ ⋯≤x(r). We present the methods of point estimation for β, θ and the interval estimation only for the shape parameter β.

3.1. Maximum Likelihood Estimation

Under the above type-II censoring, the likelihood function is
()
The partial derivatives of log-likelihood equations (∂log⁡⁡L(β, θ))/∂β = 0, (∂log⁡⁡L(β, θ))/∂θ = 0 give us
()
The maximum likelihood estimate (MLE) for θ is , where no analytic form of MLE can be obtained, and a numeric method has to be applied. The uniqueness of MLE can be shown by using the following Lemma 5 presented in Chen [6] (in which a wrong proof was given). We provide a correct proof of the lemma as well as the uniqueness of MLE in the appendix.

Lemma 5. Let with the constants a > 0, b > 0, then

  • (1)

    ()

  • (2)

    For b > a > 0, ξ(β) is strictly increasing in β > 0.

3.2. Method of Moment Estimation

It is known that , i = 1,2, …, r are the first r ordered statistics of n random samples from Exp (1), and the mean and variance of Y(i) are and , respectively [14]. We set up the following equations by the first two “ordered” moments to obtain method of moment (MOM) estimates as follows:
()
where . Therefore, the MOM estimate is with being the root of . The uniqueness of is shown in the appendix. In addition
()
is a pivotal quantity (called MOM quantity) whose distribution is unknown. Under the different values of sample size n and number of failures r, we carry out 10000 Monte-Carlo simulations to compute some quantiles of the pivotal quantity a(n, r) and the mean , listed in Table 2. Then, we suggest a modified method of moment (MMOM) estimate , the root of equation , and accordingly .
Table 2. Some quantiles of pivotal quantity a(n, r) and mean in 10000 simulations.
n r 0.995 0.975 0.95 0.90 0.10 0.05 0.025 0.005
10 8 0.1363 0.1437 0.1484 0.1545 0.2375 0.2592 0.2820 0.3361 0.1921
9 0.1251 0.1324 0.1370 0.1433 0.2255 0.2467 0.2692 0.3232 0.1803
10 0.1178 0.1259 0.1311 0.1378 0.2367 0.2649 0.2927 0.3638 0.1819
  
15 11 0.1022 0.1072 0.1104 0.1144 0.1628 0.1740 0.1851 0.2117 0.1365
12 0.0956 0.1005 0.1035 0.1073 0.1534 0.1640 0.1747 0.1998 0.1285
13 0.0902 0.0951 0.0980 0.1018 0.1473 0.1582 0.1692 0.1951 0.1227
14 0.0862 0.0913 0.0944 0.0983 0.1461 0.1577 0.1695 0.1984 0.1202
15 0.0841 0.0898 0.0933 0.0978 0.1585 0.1750 0.1922 0.2333 0.1250
  
20 16 0.0740 0.0775 0.0796 0.0824 0.1123 0.1189 0.1252 0.1403 0.0963
17 0.0708 0.0744 0.0765 0.0792 0.1088 0.1154 0.1217 0.1363 0.0930
18 0.0684 0.0720 0.0742 0.0768 0.1071 0.1139 0.1204 0.1363 0.0908
19 0.0665 0.0704 0.0726 0.0754 0.1081 0.1156 0.1230 0.1405 0.0905
20 0.0661 0.0702 0.0728 0.0760 0.1185 0.1297 0.1410 0.1690 0.0952
  
25 20 0.0605 0.0633 0.0649 0.0670 0.0885 0.0928 0.0970 0.1067 0.0770
21 0.0586 0.0613 0.0629 0.0649 0.0861 0.0905 0.0948 0.1040 0.0748
22 0.0568 0.0596 0.0612 0.0632 0.0846 0.0890 0.0933 0.1031 0.0732
23 0.0555 0.0584 0.0600 0.0620 0.0842 0.0890 0.0937 0.1042 0.0723
24 0.0544 0.0575 0.0593 0.0614 0.0857 0.0911 0.0964 0.1095 0.0727
25 0.0546 0.0580 0.0600 0.0625 0.0942 0.1022 0.1102 0.1312 0.0769
  
30 24 0.0513 0.0536 0.0549 0.0565 0.0729 0.0762 0.0792 0.0860 0.0642
25 0.0499 0.0522 0.0534 0.0550 0.0711 0.0744 0.0774 0.0841 0.0626
26 0.0487 0.0510 0.0522 0.0538 0.0699 0.0732 0.0763 0.0832 0.0614
27 0.0477 0.0499 0.0512 0.0528 0.0691 0.0725 0.0758 0.0828 0.0605
28 0.0469 0.0492 0.0505 0.0521 0.0693 0.0729 0.0762 0.0837 0.0602
29 0.0465 0.0489 0.0503 0.0521 0.0710 0.0752 0.0792 0.0883 0.0609
30 0.0466 0.0495 0.0511 0.0531 0.0779 0.0842 0.0906 0.1068 0.0645

Furthermore, using this pivotal quantity, the 100 × (1 − α)% confidence interval for β is constructed from the roots of the equation a(n, r) = c with c the lower and upper (α/2)th quantiles under various settings of (n, r) in Table 2.

3.3. Inverse Method of Moment Estimation

It is well known that (n − i + 1)(Y(i) − Y(i−1)), i = 1,2, …, r with Y(0) = 0 is a random sample from Exp (1) [15], we define
()
By using the fact that , [16], we set up the equations by their first moments to get the root and 2Sr = 2r to get , termed as inverse method of moment (IMOM) estimates. In the case of small sample size n, we set up the equations by the distribution modes 2Sr = 2(r − 1), to get the modified inverse moment (MIM) estimates and .
The pivotal quantity (called MIM quantity) may result in a (1 − α) × 100% confidence interval for β with the lower and upper limits from the equations
()
with .
In what follows, we prove that the estimators and obtained above are unique. Note that
()
By Lemma 5, is strictly increasing of β for i > k and decreasing for i < k. Then, Sr/Sk is strictly increasing, so is . In addition, , then limβ→0(Sr/Sk) = 1, and thus . Also since
()
we have lim⁡β→+∞(Sr/Sk) = +∞, and thus . Hence, for any a > 0 (specifically for our case here, a = r − 1 > 0 or a = r − 2 > 0), the equation has a unique root in β > 0.
An exact confidence interval was provided in Wu et al. [11], who employed the fact that the pivotal quantities (called Wu’s exact quantity) (2(Sr − Sk)/2(r − k))/(2Sk/2k) = (k/(r − k))((Sr − Sk)/Sk) ~ F2(r−k),2k, k = 1,2, …, r − 1 to form the kth 100 × (1 − α)% confidence interval for β with the low and upper limits being the solutions from the following equation
()
where c = Fα/2,2(r−k),2k, F1−α/2,2(r−k),2k. The optimal interval is the one with the shortest width among the r − 1 intervals. Notice that the interval with k = 1 reduces to the one constructed in Chen [6]. Wu et al. [11] also provided an approximated interval estimation by using the idea of Mann et al. [17] through the following pivotal quantities (called Wu’s approx. quantity):
()
with , . Again, the optimal is the interval with the shortest width among the r − 1 intervals.

To determine what value of k, in general, results in the optimal for Wu’s methods, we conduct a simulation study under various settings of (n, r). We only show the results for Wu’s exact interval since similar findings were obtained for Wu’s approximated method. We consider 3 ≤ k ≤ r − 3 to ensure the variance existence of F2(r−k),2k and its symmetry F2k,2(r−k). We choose the true values of parameters β = 1, θ = 1 and significance level α = 0.05 and calculate the interval estimations of parameter β based on 1000 Monte-Carlo simulations. The average upper and lower limits, average interval widths, and coverage probabilities are shown in Table 3, in which the least average interval width occurs at k = [r/3], where [·] is the greatest integer function. Thus it seems that the shortest interval is achieved when the sampling distribution is close to symmetric as much as possible.

Table 3. 95% confidence interval for β in 1000 simulations by Wu’s exact.
n r k Average Average Average Coverage
Lower limit Upper limit Interval width Probability
10 8 3 0.4016 2.6205 2.2189 0.956
4 0.3626 2.7726 2.4100 0.951
5 0.3293 3.3279 2.9986 0.961
9 3 0.4493 2.3191 1.8699 0.953
4 0.4183 2.3419 1.9237 0,951
5 0.4190 2.7233 2.3043 0.942
  
15 13 3 0.5218 2.0465 1.5247 0.951
4 0.5113 2.0149 1.5036 0.946
5 0.5113 2.0591 1.5478 0.945
14 3 0.5350 1.9170 1.3820 0.951
4 0.5267 1.8683 1.3415 0.956
5 0.5238 1.8768 1.3530 0.968
  
20 16 4 0.5443 1.9095 1.3652 0.951
5 0.5324 1.8901 1.3577 0.956
6 0.5350 1.9469 1.4120 0.954
7 0.5248 1.9774 1.4526 0.954
17 4 0.5576 1.8412 1.2836 0.955
5 0.5490 1.8199 1.2709 0.951
6 0.5599 1.8739 1.3140 0.953
7 0.5420 1.8670 1.3250 0.962
18 5 0.5759 1.7837 1.2078 0.945
6 0.5658 1.7607 1.1948 0.956
7 0.5673 1.7889 1.2216 0.943
8 0.5615 1.8075 1.2460 0.957
  
25 20 5 0.5833 1.7904 1.2071 0.951
6 0.5726 1.7644 1.1918 0.942
7 0.5838 1.8197 1.2359 0.951
8 0.5695 1.8198 1.2503 0.962
21 6 0.5934 1.7386 1.1452 0.944
7 0.5854 1.7279 1.1425 0.946
8 0.5749 1.7237 1.1488 0.950
9 0.5810 1.7754 1.1944 0.951
22 6 0.6034 1.6876 1.0842 0.951
7 0.5974 1.6753 1.0779 0.949
8 0.5910 1.6730 1.0820 0.949
9 0.5925 1.6984 1.1060 0.947
  
30 25 7 0.6201 1.6580 1.0378 0.952
8 0.6097 1.6447 1.0350 0.946
9 0.6080 1.6520 1.0439 0.950
10 0.6084 1.6730 1.0646 0.954
26 7 0.6301 1.6321 1.0020 0.944
8 0.6219 1.6100 0.9881 0.951
9 0.6193 1.6158 0.9965 0.946
10 0.6166 1.6181 1.0016 0.958
27 8 0.6389 1.5909 0.9520 0.945
9 0.6303 1.5768 0.9465 0.955
10 0.6324 1.5931 0.9607 0.948
11 0.6298 1.5955 0.9657 0.947

4. Simulation Study

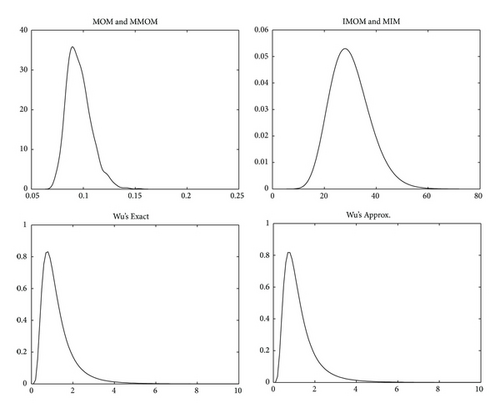
We investigate the precisions of presented point and interval estimation methods by Monte-Carlo simulations. We choose the true values of parameters β = 1, θ = 1, under which the density curve is shown in Figure 1(a), whose time scale is approximately 0 to 2. We generate 1000 random samples for each case of (n, r) in Table 4. The range of sample values is somehow related to the settings of (n, r). For example, the range of r = 8 observed values is 0.051 to 0.981 under n = 10, r = 8, while they are 0.0284 to 1.362 for n = 20, r = 18, and 0.018 and 1.483 for n = 30, r = 30. The point estimates of parameters β, θ for the 1000 generated samples under each case of (n, r) are calculated. Table 4 lists the mean and mean square error (MSE) of these estimates, among which MIM consistently produces the smallest MSE for the estimates and interestingly performs better than MLE under moderate sample size. To make more comparison, we also computed MOM estimates based on Wu’s exact quantity by setting up the equations through the first moments of , k = 1,2, …, r − 1. The least MSE occurs at k = [r/3] as well, and it lies (not shown in the table) between MSEs of MMOM and IMOM, so is larger than MIM’s. The 95% confidence intervals for β are also computed based on these simulated samples. The average upper and lower limits, average interval width and coverage probability are shown in Table 5, where Wu’s exact method in (12) selects the optimal interval estimation with k = [r/3]. It can be seen that MIM quantity in (9) produces the shortest average width of interval as well as least MSE for point estimation. We also did simulation studies under various settings of parameter values, including the case of bathtub-shape failure rate with 0 < β < 1. Similar results are obtained, showing that MIM approach consistently outperforms the other methods for both point and interval estimations (summary tables are not shown). The reason is that the log-scale expressed MIM quantity possesses less variability or its distribution is closer to symmetry than the distributions of other pivotal quantities. To illustrate this point, the density curves with n = 20, r = 16 of the four applied pivotal quantities: MOM, MIM, and Wu’s exact and approx. were shown in Figure 5, where the skewnesses of these distributions are 1.0878, 0.5164, 3.5058, and 3.5156, respectively, indicating the distribution of MIM pivot (whose skewness is 0.5164) is closest to symmetry.

Table 4. Comparison of point estimations for β (above), θ (below) with true values β = θ = 1.
n r MLE MOM MMOM IMOM MIM
Mean MSE Mean MSE Mean MSE Mean MSE Mean MSE
10 8 1.3251 0.4554 1.5849 1.0819 1.2588 0.4836 1.1701 0.3111 1.0034 0.2089
0.8921 0.1787 0.7928 0.2181 0.9077 0.1686 0.9427 0.1575 1.0073 0.1378
9 1.2712 0.3197 1.4863 0.7610 1.2325 0.3735 1.1225 0.2122 0.9882 0.1534
0.9241 0.1555 0.8650 0.1889 0.9260 0.1477 0.9604 0.1452 0.9948 0.1214
10 1.1985 0.1949 1.3882 0.5076 1.1983 0.2675 1.0959 0.1413 0.9873 0.1082
0.9933 0.1416 0.9883 0.1848 0.9879 0.1493 1.0005 0.1231 1.0088 0.1019
  
15 12 1.1955 0.1955 1.3323 0.3511 1.1466 0.1862 1.0893 0.1334 0.9907 0.1037
0.9197 0.1146 0.8448 0.1350 0.9305 0.1090 0.9704 0.1023 1.0107 0.0937
13 1.1565 0.1576 1.2694 0.2795 1.1167 0.1622 1.0744 0.1209 0.9878 0.0975
0.9515 0.1028 0.9002 0.1180 0.9567 0.0984 0.9746 0.0929 1.0016 0.0837
14 1.1349 0.1215 1.2318 0.2377 1.1073 0.1404 1.0650 0.0798 0.9887 0.0655
0.9629 0.0963 0.9346 0.1099 0.9642 0.0931 0.9784 0.0793 0.9944 0.0704
15 1.1200 0.0923 1.2292 0.2030 1.1257 0.1316 1.0525 0.0682 0.9858 0.0579
0.9853 0.0867 0.9814 0.1068 0.9832 0.0891 0.9906 0.0808 0.9960 0.0715
  
20 17 1.1305 0.1007 1.2089 0.1668 1.0958 0.1048 1.0673 0.0804 1.0023 0.0669
0.9503 0.0732 0.9069 0.0836 0.9569 0.0716 0.9717 0.0676 0.9940 0.0625
18 1.1028 0.0834 1.1752 0.1409 1.0781 0.0938 1.0492 0.0601 0.9905 0.0516
0.9621 0.0702 0.9287 0.0785 0.9629 0.0686 0.9836 0.0662 0.9991 0.0608
19 1.0948 0.0682 1.1685 0.1215 1.0867 0.0841 1.0450 0.0524 0.9915 0.0456
0.9716 0.0575 0.9502 0.0659 0.9691 0.0581 0.9857 0.0637 0.9953 0.0582
20 1.0921 0.0599 1.1683 0.1197 1.0978 0.0854 1.0371 0.0519 0.9892 0.0463
0.9974 0.0614 0.9938 0.0707 0.9954 0.0625 1.0030 0.0574 1.0061 0.0525
  
25 22 1.0801 0.0626 1.1397 0.0979 1.0597 0.0692 1.0399 0.0528 0.9925 0.0468
0.9624 0.0508 0.9294 0.0576 0.9631 0.0508 0.9824 0.0495 0.9968 0.0463
23 1.0782 0.0524 1.1362 0.0852 1.0644 0.0607 1.0358 0.0459 0.9917 0.0411
0.9746 0.0499 0.9507 0.0561 0.9741 0.0502 0.9848 0.0468 0.9952 0.0437
24 1.0789 0.0523 1.1273 0.0823 1.0656 0.0609 1.0489 0.0454 1.0075 0.0398
0.9795 0.0486 0.9649 0.0531 0.9781 0.0480 0.9876 0.0463 0.9940 0.0429
25 1.0634 0.0405 1.1251 0.0754 1.0725 0.0572 1.0267 0.0397 0.9893 0.0366
1.0019 0.0464 0.9994 0.0531 1.0007 0.0481 1.0136 0.0423 1.0158 0.0395
  
30 27 1.0679 0.0445 1.1110 0.0683 1.0494 0.0508 1.0310 0.0387 0.9934 0.0351
0.9775 0.0449 0.9536 0.0483 0.9775 0.0441 0.9831 0.0409 0.9933 0.0387
28 1.0649 0.0399 1.1101 0.0617 1.0556 0.0467 1.0293 0.0342 0.9939 0.0312
0.9755 0.0408 0.9590 0.0451 0.9756 0.0412 0.9846 0.0389 0.9922 0.0367
29 1.0606 0.0379 1.0957 0.0572 1.0492 0.0451 1.0386 0.0352 1.0052 0.0317
0.9845 0.0404 0.9746 0.0425 0.9839 0.0395 0.9860 0.0370 0.9909 0.0349
30 1.0549 0.0315 1.1104 0.0593 1.0677 0.0464 1.0159 0.0298 0.9853 0.0282
1.0014 0.0373 0.9980 0.0421 0.9992 0.0389 1.0046 0.0368 1.0065 0.0348
Table 5. Width comparison of interval estimations for 1000 simulations.
n r Wu’s exact MOM pivot MIM pivot
(coverage probability) (coverage probability) (coverage probability)
10 8 2.2189 (0.956) 2.4262 (0.962) 1.6850 (0.951)
9 1.8699 (0.953) 2.0865 (0.960) 1.4650 (0.954)
10 1.5398 (0.954) 1.8407 (0.957) 1.2372 (0.952)
  
15 12 1.5989 (0.946) 1.6231 (0.958) 1.2542 (0.956)
13 1.5036 (0.946) 1.5421 (0.946) 1.1714 (0.955)
14 1.3415 (0.956) 1.3138 (0.949) 1.0601 (0.953)
15 1.1966 (0.956) 1.2606 (0.951) 0.9537 (0.949)
  
20 16 1.3577 (0.956) 1.2771 (0.952) 1.0681 (0.950)
17 1.2709 (0.951) 1.2150 (0.961) 1.0018 (0.963)
18 1.1948 (0.956) 1.1268 (0.953) 0.9360 (0.955)
19 1.1022 (0.950) 1.0185 (0.943) 0.8821 (0.960)
20 1.0075 (0.950) 1.0016 (0.947) 0.8100 (0.950)
  
25 20 1.1918 (0.942) 1.0922 (0.943) 0.9306 (0.948)
21 1.1425 (0.946) 1.0411 (0.959) 0.8896 (0.950)
22 1.0779 (0.949) 0.9787 (0.954) 0.8455 (0.953)
23 1.0166 (0.945) 0.9380 (0.954) 0.8025 (0.955)
24 0.9526 (0.946) 0.8832 (0.948) 0.7578 (0.960)
25 0.8863 (0.951) 0.8644 (0.943) 0.7149 (0.953)
  
30 24 1.0806 (0.950) 0.9752 (0.954) 0.8420 (0.949)
25 1.0350 (0.946) 0.9187 (0.945) 0.8086 (0.956)
26 0.9881 (0.951) 0.8959 (0.951) 0.7785 (0.956)
27 0.9465 (0.955) 0.8407 (0.955) 0.7454 (0.961)
28 0.9022 (0.956) 0.8212 (0.945) 0.7150 (0.951)
29 0.8543 (0.943) 0.7807 (0.941) 0.6792 (0.954)
30 0.8039 (0.955) 0.7714 (0.947) 0.6438 (0.948)
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Densities of pivotal quantities with n = 20, r = 16.

5. Illustrative Examples

In this section, we apply the presented approaches on two examples to compare the efficiency of estimation methods.

Example 6. Wu et al. [11] presented a complete failure hour of 18 electronic equipments: 5, 11, 21, 31, 46, 75, 98, 122, 145, 165, 195, 224, 245, 293, 321, 330, 350, and 420. Xie et al. [18] showed that the data had bathtub failure rate function, so we fit this dataset by CZM(β, θ) to obtain the estimation results summarized in Table 6. In this case of relatively small sample size n = 18, MIM should yield reliable estimates based on the simulation study. From the results of the 95% confidence interval for β, one may see that the shortest Wu’s exact interval occurs at k = 7, a little narrower than that of Wu’s exact with k = [18/3] = 6. This indicates that maybe the data slightly deviate from CZM(β, θ). Although Wu’s approx. gives a shorter width than that from Wu’s exact, it is a large-sample based approach whose coverage probability might not be the same as the nominal under the small sample size. Overall, MIM pivot produces the shortest interval among all the methods in accordance with the findings in the simulation study.

Table 6. Estimation results using data in Wu et al. [11].
Parameter MLE MOM MMOM IMOM MIM
β 0.2893 0.3102 0.3005 0.2806 0.2741
θ 100.4048 189.7327 139.5206 78.9727 66.6931
  
Approach 95% confidence interval for β Length
  
Chen’s (Wu’s exact k = 1) (0.1986, 0.3697) 0.1771
Wu’s exact (k = 7) (0.2106, 0.3299) 0.1193
Wu’s exact (k = 6) (0.2066, 0.3261) 0.1195
Wu’s approximated (k = 5) (0.2122, 0.3220) 0.1098
MOM pivot (0.2304, 0.3640) 0.1336
MIM pivot (0.2237, 0.3260) 0.1023

Example 7. Chen [6] presented a type-II censoring data of n = 15 samples from CZM(0.5,50), in which there was r = 11 complete failures: 0.29, 1.44, 8.38, 8.66, 10.20, 11.04, 13.44, 14.37, 17.05, 17.13, and 18.35. Notably, since β = 0.5 < 1, the data was from the distribution with a bathtub-shaped failure rate. The estimation results by the proposed methods are shown in Table 7, where we notice that some methods perform better than MIM (particularly for the estimation of β), but not significantly. Despite only 11 complete failures out of 15 samples used in the estimation, MIM still yields a comparable point estimates. For the 95% confidence interval of β, Wu’s exact and approx. with k = [11/3] = 3 produce the least lengths among all intervals for k = 1,2, …, 10. Also MIM pivot gives the shortest length of interval as expected. In summary, although it is an example of bathtub-shaped failure rate, the results are in accordance with the findings in the simulation study, where the comparisons are based on the data generated from a nonbathtub shaped failure rate function with β = 1.

Table 7. Estimation results using data in Chen [6].
Parameter MLE MOM MMOM IMOM MIM
β 0.5068 0.5471 0.5071 0.4648 0.4584
θ 63.8939 102.2165 64.7495 40.3122 41.5428
  
Approach 95% confidence interval for β Length
  
Chen’s (Wu’s exact k = 1) (0.1900, 0.6200) 0.4300
Wu’s exact (k = 3) (0.3783, 0.7049) 0.3266
Wu’s approximated (k = 3) (0.3803, 0.6957) 0.3154
MOM pivot (0.3013, 0.6492) 0.3479
MIM pivot (0.2955, 0.5998) 0.3043

6. Conclusions

In this paper, we consider the parameter inference for a two-parameter life distribution. We present five point estimations and three interval estimations for the parameter of interest. Through the Monte-Carlo simulation technique, we determined a mechanism to obtain the optimal interval estimation originally proposed by Wu et al. [11]. The performance of the methods were assessed by a comparison of estimation precisions, and it showed that the MIM pivotal quantity with a log-scale expression leads to a relative effectiveness of the estimation under moderate sample size. This indicated that the quantity has less variability or its distribution is closer to symmetry. We applied the methods to two datasets and demonstrated the efficiency of MIM estimation method.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

Wang and Xu’s work was supported by the Grants from Innovation Program of Shanghai Municipal Education Commission (14YZ080, 14ZZ155). Wang’s work was also supported by Shanghai Normal University SK201306. Sha’s work was partially supported by NSF CMMI-0654417, and NIH NIMHD-8G12MD007592.

    Appendix

    Proof of Lemma 1. (1) When β = 1, we have f′(x) = (1 − ex/θ)/θexp⁡(x + (1 − ex)/θ). Obviously, f′(x) < 0 when 0 < θ ≤ 1, and f(x) is unimodal at x0 = log⁡⁡θ when θ > 1.

    For β ≠ 1, first we have

    ()
    Let , then obviously limx→0g(x) = (β − 1)θ, limx→+∞g(x) = −∞, and . Let , then and limx→0g1(x) = θ − 1, limx→+∞g1(x) = −∞. (i) for 0 < θ ≤ 1, we have g1(x) < 0, and thus g′(x) < 0. (ii) for θ > 1, there is a unique positive root x1 of g1(x) = 0, resulting in g1(x) > 0, g′(x) > 0 in 0 < x < x1, and g1(x) < 0,  g′(x) < 0 in x > x1.

    (2) When β > 1, we know limx→0g(x) = (β − 1)θ > 0, so there exists a unique positive root x0 of g(x) = 0. Therefore, g(x) > 0, and then f′(x) > 0 in 0 < x < x0, but g(x) < 0, then f′(x) < 0 in x > x0, as a result f(x) is unimodal.

    (3) When 0 < β < 1, then limx→0g(x) = (β − 1)θ < 0, limx→+∞g(x) = −∞. Note that limx→0f(x) = +∞, limx→+∞f(x) = 0. (i) for 0 < θ ≤ 1, then we have g′(x) < 0, and so g(x) < 0, thus f′(x) < 0, that is, f(x) is decreasing; (ii) for θ > 1, (a) if g(x1) ≤ 0, then we have g(x) ≤ 0, f′(x) ≤ 0, that is, f(x) is decreasing; (b) if g(x1) > 0, then there are two positive roots x01, x02 of g(x) = 0 with 0 < x01 < x1 < x02. First for 0 < x < x01, we have g(x) < 0, f′(x) < 0, and so f(x) is decreasing. Secondly for x01 < x < x02, we have g(x) > 0, f′(x) > 0, and so f(x) is increasing. Finally for x > x02, we have g(x) < 0, f′(x) < 0, and so f(x) is decreasing.

    The following mathematical result will be used in the proof of Theorem 4.

    Lemma A.1 (see [19].)Let g(x) be a nonnegative function at [a, +∞) and integrable at [a, b] for any b > a. If lim⁡x→+∞((log⁡⁡g(x))/log⁡⁡x) = p, then is convergent for −∞ ≤ p < −1, and divergent for −1 < p ≤ +∞.

    Proof of Theorem 4. (1) The kth moment is

    ()
    Let the integrand function and then by L’Hopital’s rule with t = xβ
    ()
    Thus the kth moment exists by Lemma A.1.

    (2) , so . Setting the function , we have limx→0g(x) = 0, limx→+∞g(x) = +∞, and , then

    • (i)

      when β ≥ 1, we have g′(x) > 0, then g(x) > 0, G′(x) > 0, that is, G(x) is increasing;

    • (ii)

      when 0 < β < 1, let x0 = ((1 − β)/β)1/β, and then we have g′(x) < 0 in 0 < x < x0 and g′(x) > 0 in x > x0. Also g(x0) = 1 − βe(1 − β)/β < 0, therefore, there exists a root x1 of g(x) = 0 with x1 > x0 > 0. Then we have g(x) < 0, G′(x) < 0, so G(x) is decreasing in 0 < x < x1, and g(x) > 0, G′(x) > 0, so G(x) is increasing in x > x1. That is G(x) is a bathtub-shape (concave-up) function.

    (3) , then

    ()
    Let , then
    ()
    • (i)

      When β > 1, we have g′(x) > 0, limx→0g(x) = −∞, limx→+∞g(x) = 0, so g(x) < 0, and thus m′(x) < 0.

    • (ii)

      When β = 1, we have g′(x) = θe−xexp⁡((1 − ex)/θ) > 0, , limx→+∞g(x) = 0, so g(x) < 0, m′(x) < 0.

    • (iii)

      When 0 < β < 1, with x0 = ((1 − β)/β)1/β, we get g′(x) < 0 in 0 < x < x0 and g′(x) > 0 in x > x0. Also , limx→+∞g(x) = 0, and = since (1 − β)t−β − β < 0 in t > x0. Thus, there is a unique root x1 of g(x) = 0 with 0 < x1 < x0, so that g(x) > 0, m′(x) > 0 in 0 < x < x1 and g(x) < 0, m′(x) < 0 in x > x1. That is, m(x) is unimodal.

    Proof of Lemma 5. The proof of (1) is clear, therefore we only show the proof for (2). Chen [6] gave a proof, but it was wrong since in general two increasing functions, say f(x), g(x) can not guarantee the product f(x)g(x) being increasing unless both f(x) and g(x) are positive functions. Here we give the correct proof as follows.

    Since , then

    ()
    To show ξ′(β) > 0, it is desired to prove that the function is strictly increasing in s > 0. To make the notation simple, let x = sβ, and f(x) = (xexlog⁡⁡x)/(ex − 1) = (xlog⁡⁡x)/(1 − e−x), we have . Note that , then .

    (i) for x ≥ 1, obviously log⁡⁡x ≥ 0, and so g(x) > 0.

    (ii) for 0 < x < 1, first k + 1 + xlog⁡⁡x ≥ 2 + xlog⁡⁡x for k ≥ 1. Additionally, we know g1(x) = 2 + xlog⁡⁡x is a concave-up function in 0 < x < 1 with achieving minimum value g1(e−1) = 2 − e−1 > 0, so g1(x) > 0, and then g(x) > 0 in 0 < x < 1.

    In conclusion, we obtain g(x) > 0 in x > 0, and so f′(x) > 0, that is, f(x) is strictly increasing in x > 0. The lemma follows.

    Proof of Uniqueness of MLE. We denote the left side of the second equation in (4) as H(β). It is obvious that limβ→0H(β) = −∞. Now we consider limβ→+∞H(β) for various cases by using Lemma 5.

    (1) When x(r) ≤ 1, then x(i) < 1, i = 1,2, …, r − 1. Note that

    ()
    with , , i < r, = and (since x(i) < x(r)), we have .

    (2) When x(r) > 1, note that

    ()
    with , , i < r, , then .

    In conclusion, H(β) is increasing and limβ→0H(β) = −∞, limβ→+∞H(β) > 0, thus the equation H(β) = 0 must have a unique positive root.

    Proof of Uniqueness of MOM. Let , then

    ()
    Obviously, for x > 0, and we would like to show the last function being positive in the above expression. Let and , we have , and from the proof of Lemma 5. Then by the Mean Value Theorem, there are ξ1,  ξ2 with min⁡(x(i), x(j)) < ξ1, ξ2 < max⁡(x(i), x(j)) satisfying
    ()
    Hence, we obtain H′(β) > 0, that is, H(β) is increasing. Also limβ→0H(β) = r(e−1)2/[r(e−1)]2 = 1/r, and from
    ()

    Additionally, on the one hand, , and on the other hand

    ()
    So . Thus, the equation has a unique root in β > 0.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.