Several oscillation results are proposed including necessary and sufficient conditions for the oscillation of fractional-order delay differential equations with constant coefficients, the sufficient or necessary and sufficient conditions for the oscillation of fractional-order delay differential equations by analysis method, and the sufficient or necessary and sufficient conditions for the oscillation of delay partial differential equation with three different boundary conditions. For this, α-exponential function which is a kind of functions that play the same role of the classical exponential functions of fractional-order derivatives is used.

1. Introduction

For the past three centuries, fractional calculus has been dealt with by mathematicians. In the recent decades, it is widely used in the fields of engineering, science, and economy. Recently, fractional differential systems have gained scholar’s attention [1–3]. Many researchers demonstrated applications of fractional calculus in the frequency dependent damping behavior of many viscoelastic materials, dynamics of interfaces between nanoparticles and substrates, the nonlinear oscillation of earthquakes, bioengineering, continuum and statistical mechanics, signal processing, filter design, circuit theory, and robotics. In some practical systems, such as economic systems, biological systems, and space-light industry systems, due to the transmission of the signal or the mechanical transmission, the research on fractional differential systems with delay is desired.

In [2], the authors described the application of the background and significance of the differential delay equations oscillation and fractional differential equations. The delay differential equation is different from ordinary differential equations. Moreover, compared with the periodic solution, oscillatory solution has more extensive application prospect and theory value in terms of the general solution of equation. In this paper, the necessary or sufficient conditions for the oscillation of several fractional-order delay differential equations are analyzed and discussed. Some oscillation results are proposed for the fractional-order linear delay differential equation as follows:

(1)

where 0 < α < 1. Some oscillation results are also given for the delay parabolic differential equation as follows:

(2)

For the purpose, known methods are expanded for our results.

2. Preliminaries

We first give some definitions and make some preliminaries. The fractional-order derivative D^αx(t) can be defined in different ways, wherein Riemann-Liouville’s definition and Caputo’s definition are two main expressions as follows.

Definition 1. Riemann-Liouville’s fractional order derivative [3, 4] is defined by

(3)

where

is the Gamma function.

Caputo’s fractional order derivative is defined by

(4)

Definition 2. α-exponential function is as follows [2]:

(5)

where

satisfies the differential equation

, (t > 0).

The derivative has the property of

(6)

Mittag-Lefflerfunction [3, 4] can be defined by

(7)

The first order delay differential equation including fractional-order derivative [2] is expressed by

(8)

where p, q, T ∈ R, 0 < α < 1. Since α is a positive rational number, let α = k/n = kβ satisfy 0 < α < 1. The expression for (1) with constant coefficients is given by

(9)

where

(10)

Equation (10) is the characteristic polynomial of (8). The contribution in [2] is considered.

Lemma 3. The following statements are equivalent.

(1)
Every solution of (8) oscillates.
(2)
The characteristic equation (10) has no real roots.

In this paper, the main results are derived from the application of the basic theory in [2]. The oscillation or nonoscillation of solutions for several fractional-order delay differential equations can be obtained based on these main results.

3. Main Result

3.1. The Fractional-Order Delay Differential Equation with Constant Coefficients

The general form of the fractional-order linear delay differential equation is

(11)

Since

, the characteristic polynomial of (11) is as follows:

(12)

The detailed derivation can be found in Appendices A, B, and C. Using Lemma 3, we have the necessary and sufficient conditions for oscillation of all solutions of (11) as follows.

Corollary 4. The following statements are equivalent.

(1)
Every solution of (11) oscillates.
(2)
The characteristic equation (12) has no real roots.

In order to use Corollary 4 more effectively, Theorem 6 is proposed. Before presenting the theorem, the function

(0 < t < +∞) is given (see Appendices A, B, and C for details), and the maximum of g(t) is as follows:

(13)

Lemma 5.

(1)
If or p < 0, (12) has a real root.
(2)
If , (12) has not a real root.

Proof. (1) If p < 0, it is obvious that (12) has a real root.

As p > 0, from the characteristic equation (12),

(14)

So p < 0 or , and (12) has a real root.

(2) In the same way, we get , and (12) has not a real root.

Theorem 6.

(1)
If or p < 0, the solution of (11) is nonoscillatory.
(2)
If , the solution of (11) is oscillatory.

Proof. The equation has a solution , if and only if λ is a root of characteristic of equation . Using the conditions for (11), we have the following.

(1)
If or p < 0, (12) has a real root, and the solution of (11) is nonoscillatory.
(2)
If , (12) does not have a real root, and the solution is oscillatory. So we can obtain , and the solutions of (11) are oscillatory. Therefore, the proof of the theorem can be completed.

Example 7. We consider delay differential equation with fractional-order derivatives

(15)

(16)

All the conditions of Theorem 6 are satisfied. Fractional derivative of some special functions is as D^1/2sint = sin(t + π/4). Thus, all the solutions of (15) are oscillatory. One of such solutions is x(t) = sint.

We consider the following fractional-order linear delay differential equation:

(17)

(H₁): u > 0, f(u) ≥ Cu.

Theorem 8. Assume that (H) holds, and are satisfied. Every solution of the delay differential equation (17) oscillates.

Proof. We may assume that (17) has eventually positive solution. Then, there exists t₀, and if t > t₀, , x(t) > 0, and x(t − T) > 0.

We consider the eventually positive solution of the following inequality:

(18)

Assume the inequality (18) has a solution :

(19)

If , the inequality does not have a real root. That means every solution of the inequality (18) is oscillatory. Thus, if , every solution of the delay differential equation (17) oscillates.

3.2. The Fractional-Order Delay Differential Equation with Oscillating Coefficients

We consider oscillation of solutions of the fractional-order delay differential equation with oscillating coefficients:

(20)

Let

. If t is sufficiently large,

(21)

We have the sufficient conditions for oscillation of all solutions of (20) as follows.

Theorem 9. If t is sufficiently large, . Then, the solution of (20) is oscillatory.

Proof. Assume that (20) has eventually positive solution. If there exists t₀ > 0 such that t > t₀, then x(t) > 0, x(t − T) > 0,

(22)

(23)

(24)

Similar to the proof process of Theorem 8, every solution of the inequality (24) is oscillatory due to . Thus, the inequality (24) does not have eventually positive solution. Therefore, if t is sufficiently large, , and every solution of (20) is oscillatory. The proof of the theorem is complete.

We consider the following fractional-order linear delay differential equations:

(25)

(26)

Their characteristic equations are expressed by (27) and (28), respectively:

(27)

(28)

where a, λ₀, p_k, q_k, T_k, σ_k are nonnegative constants.

Based on Lemma 3, the statements are equivalent for oscillation of all solutions of (25) and (26) as follows.

Corollary 10. The following statements are equivalent.

(1)
Every solution of (25) and (26) oscillates.
(2)
The characteristic equations of (27) and (28) have no real roots.

4. The Fractional-Order Delay Partial Differential Equation

To research the oscillation properties of solutions for delay partial differential equations, we consider the delay parabolic differential equations [5]:

(29)

where (x, t) ∈ Ω × (t, ∞) = G. ∂Ω is the bounded region with piecewise smooth in Rⁿ.

The hypotheses are always true as follows.

(C₁) a, b_k ∈ C([0, ∞); [0, ∞)), and q is a nonnegative constant.
(C₂) T, σ_k are nonnegative constants.

Consider the boundary conditions as follows:

where N is the unit exterior normal vector in ∂Ω.

If there are no special instructions in this section, we only discuss the oscillation of solutions of the fractional-order delay partial differential equation with respect to time variable t.

Theorem 11. Assume that (C₁) and (C₂) hold, and (B1) is satisfied.

(1)
As or q < 0, the solution of (29) and (B1) is nonoscillatory.
(2)
As , the solution of (29) and (B1) is oscillatory.

Proof. Let (x, t) ∈ Ω × [t₁, ∞). Equation (29) on both sides of the integral of x in Ω is expressed by

(30)

By using Green’s formula and boundary conditions (B1),

(31)

Let . Substituting (30) with (31),

(32)

Based on Corollary 10, (1) and (2) in Theorem 14 are proved.

Example 12. Consider the parabolic equation:

(33)

Because of , all the conditions in Theorem 11 (1) are satisfied. By using Theorem 11, every solution of (33), with

(34)

oscillates in (0, π) × R⁺. One of such solutions is u(x, t) = sintcos⁡2x.

For the more general equation of (29) with coefficients,

(35)

There are the boundary conditions as follows:

where N is the unit exterior normal vector in ∂Ω.

Assume that

(C₃) p_j, q_j, T_j, σ_j are nonnegative constants.

Some sufficient conditions for oscillation of all solutions of (35) with (B2) and (B3) are established in Theorem 15. Before presenting the theorem, the lemma is given as follows.

Lemma 13. For the Dirichlet problem,

(36)

where λ is a constant. The smallest eigenvalue λ₀ of problem (36) is positive, and the corresponding eigenfunction Φ(x) is also positive on x ∈ Ω [5]. With each solution u(x, t) of problem (35) with the boundary condition (B2), the function V(t) is defined as

(37)

Theorem 14. Assume that (C₁) and (C₃) hold, and (B2) is satisfied. Every solution of the delay differential equation (26) with several coefficients oscillates. Then, every solution of (35) oscillates.

Proof. Let (x, t) ∈ Ω × [t₁, ∞). If we multiply both sides of (35) by Φ(x) and integrate x in Ω, we obtain

(38)

where Φ(x) > 0, which satisfies Lemma 13.

By using Green’s formula and boundary condition (B2), we obtain

(39)

where dS is the surface element on ∂Ω. Substituting with (37), we obtain

(40)

Based on Corollary 10, the proof of the theorem can be immediately completed. Let v(t) be defined as , t > t₁, where u(x, t) denotes a solution of problem (35) with the boundary condition (B1) or (B3). Then, we obtain

(41)

Theorem 15. Assume that (C₁) (C₃) hold and (B1) is satisfied. Every solution of the delay differential equation with several coefficients (25) oscillates. Then, every solution of (35) with the boundary condition (B1) oscillates.

Proof. Let (x, t) ∈ Ω × [t₁, ∞) on the x be the definite integral in Ω. Assume that (35) with the boundary condition (B1) has a nonoscillatory solution and (35) has an eventually positive solution:

(42)

By using Green’s formula and boundary condition (B1), we obtain

(43)

where dS is the surface element on ∂Ω.

Let (t > t₁) be substituted into (42). We obtain

(44)

The detail of the proof process is similar to the proof process of Theorem 15.

Theorem 16. Assume that (C₁) and (C₂) hold and (B3) is satisfied. Every solution of the delay differential equation with the coefficients (25) oscillates. Then, every solution of (35) with the boundary condition (B3) oscillates.

Proof. Let (x, t) ∈ Ω × [t₁, ∞) on the x be the definite integral in Ω. For the sake of contradiction, assume that (35) with the boundary condition (B3) has a nonoscillatory solution and (35) with the boundary condition (B1) has an eventually positive solution:

(45)

By using Green’s formula and boundary condition (B3), we obtain

(46)

where dS is the surface element on ∂Ω. Let

(t > t₁) be substituted into (45). We obtain

(47)

The detail of the proof process is similar to the proof process of Theorem 15.

The delay parabolic differential equations are expressed by

(48)

Consider the boundary conditions, as shown in (B1) where N is the unit exterior normal vector in ∂Ω.

(C₄) T_k, σ_i are nonnegative constants.
(C₅) a(t), b_k(t), q_i(t) ∈ C([0, ∞); [0, ∞)), k = 1, 2, …, m; i = 1, 2, …, n; where q_i = inf⁡q_i(t) is a nonnegative constant.
(H₂) f_i(u) ∈ C(R, R), and u > 0, f_i(u) ≥ c_i u, i = 1, 2, …, n.

Theorem 17. Assume that (C₄), (C₅), and (H₂) hold and (B1) is satisfied. If , the solution of (48) with the boundary condition (B1) is oscillatory.

Proof. Let (x, t) ∈ Ω × [t₁, ∞). Assume that (48) with the boundary condition (B2) has no oscillation solutions, and (48) has eventually positive solution. If there exists t₂ > t₁ such that t > t₂, then u(x, t) > 0, u(x, t − T_k) > 0, u(x, t − σ_j) > 0. If (H₂) is satisfied, (48) can be transformed into the inequality as follows:

(49)

The inequality (49) on both sides of the integral of x in Ω is expressed by

(50)

By using Green’s formula and boundary conditions (B1), we obtain

(51)

Substituting (50) with (51) and , we obtain

(52)

By using Theorem 9, the proof of the theorem can be completed.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

The authors thank Mr. Weisheng Xu for useful discussions on the proof process in the paper.

Appendices

A. Maximum of

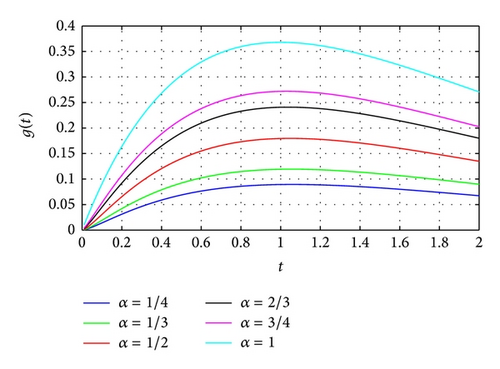
Figure 1 illustrates the curves of the function with different α. From bottom to top, α = 1/4, 1/3, 1/2, 2/3, 3/4, and 1, respectively. From Figure 1, it can be observed that there exists M such that (ω ≥ 1). In detail, the values of g(t) with different α are reported in Table 1. m is the maximum for a fixed α in Table 1.

Table 1. Values of g(t) with different α.

	α = 1/4	α = 1/3	α = 1/2	α = 2/3	α = 3/4	α = 1
t = 0.9	0.0881072	0.1176864	0.1774485	0.2383790	0.2694375	0.3659126
t = 0.95	0.0887969	0.1185872	0.1787170	0.2399068	0.2710383	0.3674039
t = 1	0.089205	0.1191138	0.1794311	0.2407091	0.2718332	0.3678794 (m)
t = 1.01	0.0892548	0.1191774	0.1795119	0.2407885	0.2719021	0.3678611
t = 1.02	0.0892949	0.1192275	0.1795730	0.240842	0.2719425	0.3678068
t = 1.03	0.0893251	0.1192646	0.1796147	0.2408705	0.2719547 (m)	0.3677171
t = 1.04	0.0893456	0.1192889	0.1796375	0.2408740 (m)	0.2719395	0.3675928
t = 1.05	0.0893567	0.1193007 (m)	0.1796417 (m)	0.2408533	0.2718973	0.3674346
t = 1.06	0.0893585 (m)	0.1193001	0.1796277	0.2408087	0.2718286	0.3672431
t = 1.07	0.0893512	0.1192875	0.1795959	0.2407409	0.2717341	0.3670191
t = 1.08	0.0893351	0.1192631	0.1795465	0.2406501	0.2716142	0.3667631
t = 1.09	0.0893102	0.1192271	0.1794801	0.2405370	0.2714694	0.3664759
t = 1.1	0.0892768	0.1191797	0.1793968	0.2404020	0.2713003	0.3661581
t = 1.15	0.0889875	0.1187809	0.17874	0.2394135	0.2701071	0.364132285
t = 1.2	0.0885098	0.1181318	0.1777141	0.2379416	0.2683777	0.361433054

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Curves of function (t > 0) with different α.

B. Supplementary Comment of g(t)

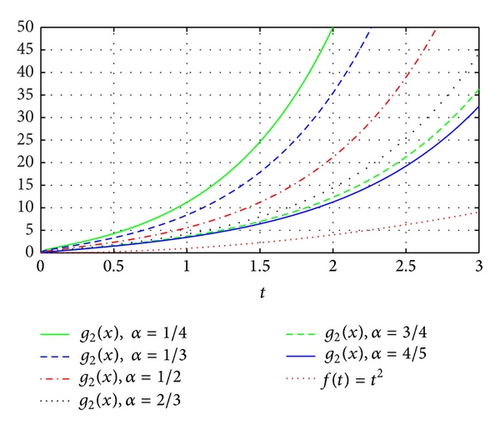
The curves of function and g₃(t) = t² (t > 0) are showed in Figure 2. The function g₂(t) is a supplementary comment of the maximum value of g(t). From top to bottom, α = 1/4, 1/3, 1/2, 2/3, 3/4, and 4/5, respectively.

C. The Characteristic Equation

The Laplace transforms for two fractional derivatives with 0 < α < 1 [6] are expressed as follows:

(C.1)

The fractional Laplace transform [2] is

. There exist M and μ such that

. By taking the Laplace transforms on both sides of (11),

(C.2)

where

. σ₀ denotes the abscissa of convergence of X(s); that is, σ₀ = inf⁡{σ ∈ R∣x(σ) exists}.

In the most general form F(s)X(s) = Q(s), we can obtain and Q(s) = x(0) − ph(sT). F(s) and Q(s) are both entire functions. Assume F(s) ≠ 0 for all real s. X(s) can be expressed as X(s) = Q(s)/F(s), Res > s₀ > 0. Therefore, is the characteristic polynomial of (11).

References

1 Wei J., The constant variation formulae for singular fractional differential systems with delay, Computers & Mathematics with Applications. (2010) 59, no. 3, 1184–1190, https://doi.org/10.1016/j.camwa.2009.07.010, MR2579482, 2-s2.0-74149083252.
10.1016/j.camwa.2009.07.010
Web of Science® Google Scholar
2 Bolat Y., On the oscillation of fractional-order delay differential equations with constant coefficients, Communications in Nonlinear Science and Numerical Simulation. (2014) 19, no. 11, 3988–3993, https://doi.org/10.1016/j.cnsns.2014.01.005, MR3212792.
10.1016/j.cnsns.2014.01.005
Web of Science® Google Scholar
3 Arikoglu A. and Ozkol I., Solution of fractional differential equations by using differential transform method, Chaos, Solitons and Fractals. (2007) 34, no. 5, 1473–1481, https://doi.org/10.1016/j.chaos.2006.09.004, MR2335397, ZBL1152.34306, 2-s2.0-34250215244.
10.1016/j.chaos.2006.09.004
Web of Science® Google Scholar
4 Trujillo J. J., Rivero M., and Bonilla B., On a Riemann-Liouville generalized Taylor′s formula, Journal of Mathematical Analysis and Applications. (1999) 231, no. 1, 255–265, https://doi.org/10.1006/jmaa.1998.6224, MR1670860, 2-s2.0-0042494532.
10.1006/jmaa.1998.6224
Web of Science® Google Scholar
5 Kubiaczyk I. and Saker S. H., Oscillation of delay parabolic differential equations with several coefficients, Journal of Computational and Applied Mathematics. (2002) 147, no. 2, 263–275, https://doi.org/10.1016/S0377-0427(02)00427-2, MR1933595, ZBL1011.35125, 2-s2.0-0037107467.
10.1016/S0377-0427(02)00427-2
Web of Science® Google Scholar
6 Tavazoei M. S. and Haeri M., Chaotic attractors in incommensurate fractional order systems, Physica D. (2008) 237, no. 20, 2628–2637, https://doi.org/10.1016/j.physd.2008.03.037, MR2514122, 2-s2.0-51249088596.
10.1016/j.physd.2008.03.037
Web of Science® Google Scholar

Citing Literature

All articles

The Oscillation of a Class of the Fractional-Order Delay Differential Equations

Abstract

1. Introduction

2. Preliminaries

3. Main Result

3.1. The Fractional-Order Delay Differential Equation with Constant Coefficients

3.2. The Fractional-Order Delay Differential Equation with Oscillating Coefficients

4. The Fractional-Order Delay Partial Differential Equation

Conflict of Interests

Acknowledgment

Appendices

A. Maximum of

B. Supplementary Comment of g(t)

C. The Characteristic Equation

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Oscillation of a Class of the Fractional-Order Delay Differential Equations

Abstract

1. Introduction

2. Preliminaries

3. Main Result

3.1. The Fractional-Order Delay Differential Equation with Constant Coefficients

3.2. The Fractional-Order Delay Differential Equation with Oscillating Coefficients

4. The Fractional-Order Delay Partial Differential Equation

Conflict of Interests

Acknowledgment

Appendices

A. Maximum of

B. Supplementary Comment of g(t)

C. The Characteristic Equation

References

Citing Literature

Figures

References

Related

Information