Mathematical Problems in Engineering
Volume 2014, Issue 1 248174
Research Article
Open Access

Delay-Aware Online Service Scheduling in High-Speed Railway Communication Systems

Shengfeng Xu, 

Shengfeng Xu

State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China njtu.edu.cn

Search for more papers by this author
Gang Zhu, 

Gang Zhu

State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China njtu.edu.cn

Search for more papers by this author
Chao Shen, 

Corresponding Author

Chao Shen

State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China njtu.edu.cn

Search for more papers by this author
Yan Lei, 

Yan Lei

State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China njtu.edu.cn

Search for more papers by this author
Zhangdui Zhong, 

Zhangdui Zhong

State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China njtu.edu.cn

Search for more papers by this author
First published: 24 March 2014
https://doi.org/10.1155/2014/248174
Citations: 6
Academic Editor: Hao Shen

Abstract

We investigate the downlink service scheduling problem in relay-assisted high-speed railway (HSR) communication systems, taking into account stochastic packet arrivals and quality-of-service (QoS) requirements. The scheduling problem is formulated as an infinite-horizon average cost constrained Markov decision process (MDP), where the scheduling actions depend on the channel state information (CSI) and the queue state information (QSI). Our objective is to find a policy that minimizes the average end-to-end delay through scheduling actions under the service delivery ratio constraints. To address the challenge of centralized control and high complexity of traditional MDP approaches, we propose a distributed online scheduling algorithm based on approximate MDP and stochastic learning, where the scheduling policy is a function of the local CSI and QSI only. Numerical experiments are carried out to show the performance of the proposed algorithm.

1. Introduction

Recently, high-speed railway (HSR) systems have developed rapidly all over the world. The passengers on the train will not only enjoy the short journey but also have a high demand on multimedia services. The cellular network deployed along the rail lines can provide seamless coverage and data packets delivery. However, the data transmission rate is strictly limited due to the penetration loss in traditional HSR communication systems. As an alternative solution, the relay-assisted HSR network architecture has been proposed in [1, 2], which was considered a better choice than direct transmission in case of large penetration loss [3] and becomes a promising architecture for future broadband mobile communications in providing high data-rate services [4].

We consider a relay-assisted two-hop HSR network architecture in this work. The data packets are delivered via a relay station (RS) instead of direct transmission to achieve a high data transmission rate. The passengers send service requests when the train is moving. If a large number of services are requested, the resource contention among multiple services should be resolved and an efficient scheduling scheme should be proposed, which not only considers the highly dynamic channel due to the extremely high moving speed but can also be implemented in a distributed manner with low complexity. In addition, the buffering at network devices, for example, content server and RS, is involved; it is thus important to consider not only the throughput performance but also the end-to-end (e2e) delay performance. Delay is a key quality-of-service (QoS) criterion for real-time multimedia services. As a result, we will focus on the delay issues for multimedia services and aim at developing a delay-aware scheduling algorithm for the relay-assisted HSR communication systems.

Many of the previous studies have been conducted to improve performance on scheduling and resource allocation in HSR communication systems. In order to support the e2e real-time data application, [5] studied a circuit domain latency model and employed a priority scheduling algorithm to estimate approximate service latency. In HSR networks with a cell array architecture, [6] proposed a scheduling and resource allocation mechanism to maximize the service rate by considering the channel variations and handover information. The optimal resource allocation problem in a cellular/infostation integrated HSR network has been investigated in [7], considering the intermittent network connectivity and multiservice demands. However, to the best of our knowledge, none of them has addressed the delay-aware scheduling in downlink relay-assisted HSR communication systems. Although the two-hop HSR network architecture is simple, how to schedule multiple services for such a network when taking account of stochastic packet arrivals and QoS requirements is still an open problem. This motivates us to investigate the delay-aware downlink scheduling problem for relay-assisted HSR communication systems.

The contributions of this paper are threefold. First, the two-hop scheduling problem is formulated as an infinite-horizon average cost constrained Markov decision process (CMDP) with the objective to minimize the average e2e delay under the service delivery ratio constraints. The above CMDP problem is converted into an unconstrained MDP by Lagrange theory and then the general solution of the CMDP problem is given by traditional iterative methods. Second, since the general solution could not give a simple implementable solution due to the curse of dimensionality, in order to simplify the solution and address the challenge of centralized control, we propose a distributed online scheduling algorithm based on approximate MDP and stochastic learning. A linear combination of per-node value functions is employed to approximate the value function of the associated optimality equation. Based on the per-node value functions, a distributed two-stage scheduling policy is derived, which is a function of the local state information only. Third, simulation results show that the proposed algorithm can achieve better performance in terms of e2e delay and service delivery ratio compared to conventional schemes. Moreover, the convergence of the proposed scheduling algorithm is established through simulations.

The remainder of the paper is organized as follows. Section 2 provides the details of the system model and assumptions. Section 3 presents the CMDP problem formulation and discusses the general solution. In Section 4, we propose a distributed online scheduling algorithm using approximate MDP and stochastic learning. Section 5 shows the performance evaluation results obtained through simulations. Finally, Section 6 makes some conclusions.

Notations. In this paper, |𝒜| is the cardinality of set 𝒜. 𝔼[·] denotes expectation.   Pr[·] is the probability measure. I[·] is an indicator function. ⌊x⌋ = max⁡{n ∈ ℤ∣n ≤ x} and [x] + = max⁡{x, 0}.

2. System Model and Assumptions

A relay-assisted HSR network architecture is shown in Figure 1. The cellular network deployed along the rail line can provide seamless coverage and data packets delivery. The base stations (BSs) are connected to the backbone network via wireline links. For simplicity, we assume that the bandwidth of the links from the backbone network to the BSs is sufficiently large so that the packets can be transmitted to BSs with a negligible delay. An RS with powerful antennas is installed on the top of the train to communicate with BSs. The RS is further connected to an access point (AP) which can be accessed by the users based on wireless local area network (WLAN) technologies. Thus, the two-hop wireless link consists of the BS-RS link and the AP-users link. With this two-hop architecture, radio signals do not need to penetrate into the carriages, and thus the radio signal penetration loss problem is resolved.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
System model.

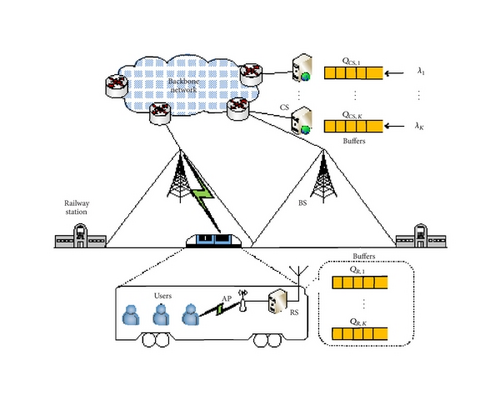
Distributed content servers are deployed in order to offload data traffic from the backbone network [8]. When a service is requested from the passengers, the data packets can be fetched from the corresponding content server (CS). To make the analysis of such network tractable, we assume each CS can provide one type of service. Notice that this can be easily extended to the situation where each CS can provide multiple types of services while one buffer is allocated to each type of service in the CS, which will be clear later on in Section 2.2. In order to simplify the protocol design for HSR applications, erasure coding based service delivery is considered [7] and the advantage is that no retransmission scheme is required for the transmission error due to a highly dynamic wireless channel condition.

Compared to the traditional cellular networks, the deterministic train trajectory in HSR networks is a unique feature [7, 9]. The train trajectory represents the location of a train at a specific time, and BS provides the service delivery if the train is under its coverage. Since the train moves on a predetermined rail line and the velocity is relatively steady, the information of train trajectory can be obtained in advance with high accuracy so that the service packets can be delivered by the specific BS at a certain time. Therefore, this paper focuses on the delay-aware service scheduling problem regardless of which BS is used for service delivery.

2.1. Physical-Layer Model

We consider a time-slotted system for downlink service transmission with slot period TB. When the train moves along the railway, BS and AP can transmit simultaneously without interference by operating on different frequency bands. For the communication in the BS-RS link, we consider the MAC frame structure proposed in [10] which is specifically designed for high-speed trains with a speed of up to 360 km/h. For the communication in the AP-users link, traditional WLAN standards, for example, IEEE 802.11a/b/g, are employed since passengers within the train are relatively stationary with respect to the AP.

Let H(t) = H1(t) ⋃   H2(t) be the joint CSI, where H1(t) = {HBS,R(t), ∀k} with the channel gain HBS,R in the BS-RS link and H2(t) = {HR,k(t), ∀k} with the channel gain HR,k between the AP and the user requesting service k. The channel from BS to the RS is assumed to follow the Rician distribution [11], while the channel between AP and the users can be treated as Rayleigh fading channel [3]. We assume that the channel gains remain constant during a slot duration and change across slots in an i.i.d. manner. In addition, to enhance transmission performance, the strong channel coding is used, and hence, the maximum achievable data rate is achieved by the instantaneous mutual information. For the BS-RS link with the bandwidth W1, the maximum achievable data rate in bit-per-second is given by
()
where PBS is the transmit power of the BS and N0 is the noise power. Since all the services share the common channel in the BS-RS link, they have the same data rate RBS. Likewise, for the AP-users link with the bandwidth W2, we have the maximum achievable data rate for service k
()
where PR is the transmit power of the AP. In addition, we assume the packets have equal size of G bits, the capacity CBS can be expressed by the maximum number of packets by converting RBS through a proportionality constant; that is, CBS = ⌊RBSTB/G⌋. Similarly, CR,k = ⌊RR,kTB/G⌋, ∀k.

2.2. Packet-Level Model

Assume that there are K types of services requested by the passengers. Each type of service is allocated with two buffers, one in the kth CS denoted by QCS,k and the other one in the RS denoted by QR,k, for k = 1, …, K. The two buffers for each service in the CSs and RS are in tandem. Let LQ be the maximum number of packets for the buffers in the RS and all CSs. Let Q(t) = Q1(t) ⋃ Q2(t) be the joint QSI, where Q1(t) = {QCS,k(t), ∀k} and Q2(t) = {QR,k(t), ∀k}. Specifically, QCS,k(t) and QR,k(t) denote the number of packets at the beginning of slot t in the buffer of kth CS and the kth buffer in RS, respectively.

These K heterogeneous services have different packet arrival rates and QoS requirements. Data packets from the higher layer application arrive into the buffers and are queued until they are transmitted. The packet arrival process for each type of service is assumed to be i.i.d. across slots. Let Ak(t) denote the number of packets arriving into the buffer in kth CS at slot t. Suppose in general, Ak(t) follows the truncated Poisson distribution fk(b) with average packet arrival rate λk = 𝔼[Ak(t)] for service k. The distribution fk(b) can be given as
()
where Jk is found assuming fk(Jk) → 0.

The average number of arriving packets at the kth CS is given by , where is the dropping probability. This is the same as the average number of packets received by the corresponding buffer in RS since the two buffers are in tandem. The sufficiently large buffer and negligible dropping probability () assumptions are considered in this paper.

2.3. MDP Model

In this paper, the service scheduling problem for the two-hop link in HSR networks is formulated as an infinite-horizon average cost CMDP. To make the analysis of the CMDP problem tractable in the sequel, it is necessary to identify the elements of MDP model in our scheduling problem. In general, an MDP model consists of five elements: decision epochs, states, actions, cost function, and state transition probability function. We describe these elements as follows.

The scheduling decisions for the data packet delivery in the two-hop link have to be made slot by slot and the instant slots are called decision epochs. Let 𝒮 and 𝒜 be the global state space and action space, respectively. 𝒮 = {S1, S2, …, S|𝒮|} = 𝒬 × ℋ, where 𝒬 is the global QSI state space and ℋ is the global CSI state space. The global system state at slot t is denoted by S(t) = (H(t), Q(t)). The action space is denoted by 𝒜 = 𝒳 × 𝒴, where 𝒳 = {xk ∈ {0,1}, ∀k} and 𝒴 = {yk ∈ {0,1}, ∀k}. xk and yk are scheduling actions for service k in the BS-RS link and AP-users link, respectively. The scheduling action is set to be 1 if the corresponding service k is scheduled and is set to 0 otherwise. Moreover, the scheduling actions should satisfy ∑k xk(t) = 1 and ∑k yk(t) = 1 at any slot t.

Given a current state S(t), the scheduling action can be decided according to a stationary policy. A stationary scheduling policy (Π) map 𝒮 to 𝒜, that is, Π : 𝒮 → 𝒜. Π is called feasible if the associated actions satisfy the constraints. We assume that the next state S(t + 1) only depends on the current state and scheduling actions but not on the previous states; hence the process {S(t)} for a given control policy Π is Markovian with the following state transition probability function:
()
where the equality holds because of the independence of channel state update processes and queue state update processes. The queue state update processes at CSs and RS are given in (5) and (6), respectively. Consider
()
()
Specifically, the dynamics of the buffers for all CSs in (5) are controlled by scheduling actions in the BS-RS link and the dynamics of the buffers in RS shown by (6) are controlled by scheduling actions in the two-hop link. Given a feasible policy Π, the induced Markov chain {S(t)} is ergodic and there exists a unique steady state distribution πS [12].
By Little’s law [13], for a sufficiently small dropping probability (), the average time that a data packet of the service k spends in the e2e system is (QCS,k + QR,k)/λk. Since the e2e delay in relay-assisted HSR networks is considered, the corresponding per-slot cost function is defined as
()

2.4. Optimization Objective and Constraints

Our goal is to find an optimal policy Π* so that the average e2e delay is minimized while satisfying the service delivery ratio constraints.

For any policy Π, the average e2e delay can be expressed as
()
where denotes the expectation with respect to the induced steady state distribution πS. The average e2e delay expressed by (8) means the average time that a data packet of all the services spends when transmitted from the CSs to users. In the MDP model, the average e2e delay can be regarded as the expected cost function. Similarly, in order to indicate heterogeneous delivery ratio requirements for different types of services, the delivery ratio constraints can be given by
()
where Tk(t) = min⁡{CR,k(t), QR,k(t)} is the maximum number of packets which can be successfully received for service k at slot t, and αk ∈ (0,1] denotes the delivery ratio requirement of service k, reflecting that the average delivery rate is proportional to the average arrival rate.

3. CMDP Problem Formulation

In this section, we formulate the delay-aware scheduling problem as an infinite-horizon average cost CMDP and discuss the general solution. The objective is to choose an optimal scheduling policy Π* so that the expected cost function (8) is minimized subject to the service delivery ratio constraints (9), which is expressed by
()
()
This problem is an infinite-horizon average cost CMDP with system state space 𝒮, action space 𝒜, the state transition probability (4), and per-slot cost function (7).

3.1. Lagrangian Approach and Unconstrained MDP

The above CMDP problem can be converted into an unconstrained MDP by Lagrange theory. As demonstrated in [14, Theorem 12.7], the optimal cost and policy of the CMDP can be obtained by an unconstrained MDP and Lagrangian approach. Firstly, the Lagrangian of (10a) and (10b) is expressed as
()
where
()
and β = [β1, β2, …, βK] T is the Lagrange multiplier (LM) vector. Hence, the corresponding unconstrained MDP is given by
()
where G(β) gives the Lagrange dual function. As shown in [15, Theorem 2.1], there exists an LM vector β≽0 such that Π* minimizes ℒ(Π, β) and the saddle point condition holds. Given an LM vector, the optimal policy Π* for (13) can be obtained by solving the associated optimality equation [12, 16] as follows:
()
where V(S) is the value function of the MDP and Pr[Sj∣Si, Π(Si)] is the state transition probability which can be obtained from (4). θ = min⁡Πℒ(Π, β) is the optimal average cost per-stage and Π*(Si) is the optimal policy minimizing the right-hand-side of (14) at any state Si. As shown in [12], the value iteration algorithm is an efficient stable iteration algorithm to solve the optimality equation, which operates by calculating successive approximation to the value function V(S) with computation complexity O(|𝒜| | 𝒮|2).

3.2. The Reduced State Optimality Equation for CMDP

The optimality equation (14) is very complicated to solve due to the huge cardinality of the system state space. In general, the channel state transition is often unavailable a priori in HSR environment. However, the statistical characteristics of the channel distribution can be obtained, which motivates us to simplify the optimality equation (14) in this subsection. By taking expectation on channel state H, the reduced state optimality equation is defined as follows:
()
where is the conditional average value function for state Qi, and is the conditional average cost and Pr[Qj∣Qi, Π(Qi)] = 𝔼H[Pr[Qj∣(Qi, H), Π(Qi, H)]] is the conditional average queue state transition probability. Instead of working on the global system state, the reduced state optimality equation (15) only depends on QSI. As shown in [17], the scheduling policy obtained by solving the optimality equation in (14) is the same as that obtained by solving the reduced state optimality equation.

4. Distributed Online Scheduling Algorithm

In certain cases of practical interest, there are still three difficulties in adopting the optimal scheduling policy presented above. Firstly, solving (15) has exponential complexity. Secondly, excessive latency may not be acceptable for real-time services due to multiple iterations. Finally, the optimal policy by solving (15) is a function of global QSI, which cannot be applied for distributed implementation. To overcome the above difficulties, we adopt the key theories of MDP and stochastic approximation and propose a distributed online scheduling algorithm, which illustrates how we could utilize the techniques of approximate MDP and stochastic learning to facilitate the distributed implementation with low complexity.

4.1. Approximate MDP

To reduce the size of the state space and decentralize the service scheduling, we approximate in (15) by the linear approximation of global value function, which is given below as
()
where is the global value function and and are regarded as per-node value functions at the buffer of kth CS and the kth buffer in RS, respectively.

We note that the dimension of the value function is greatly reduced through the linear approximation. Moreover, the per-node value function can only satisfy the optimality equation (14) in some particular states 𝒬par = {δk,q, ϕk,q∣∀ k = 1, …, K, q = 1, …, LQ}, where δk,q denotes Q1 with QCS,k = q and and ϕk,q denotes Q2 with QR,k = q and QR,k′ = 0  ∀ k′ ≠ k.

4.2. Distributed Scheduling Policy under MDP Approximation

Using the linear approximation in (16), we derive a distributed scheduling policy depending on the local CSI and QSI as well as the per-node value function of each buffer at RS and CSs. Specifically, the scheduling policy in (15) can be obtained by solving the following optimization problem:
()
()
where . Here we assume that the packet arrivals for all services follow the same distribution; that is, f(b) = fk(b)  ∀ k = 1, …, K.

From the above formula derivation, we can obtain the optimal scheduling scheme by solving (17b). Since the solution to the first link depends on the solution to the second link and vice versa, the scheduling decisions in the two-hop link are coupled. One feasible solution can be obtained by enumeration, but it cannot be distributed. In order to obtain the scheduling policy in a distributed manner, motivated by the observation in [18], we split the optimization problem into two stages, which correspond to the BS-RS link and AP-users link, respectively. In the first stage, CSs solve a local MDP problem to determine the scheduling actions in the BS-RS link. In the second stage, by using the scheduling results in the first stage, RS determines the scheduling actions in AP-users link such that the e2e delay is minimized. Specifically, these two stages are described as follows.

4.2.1. Distributed Scheduling Policy in First Stage

With the given per-node value functions and local queue state set , the scheduling policy in the first stage can be obtained by solving the following local MDP problem:
()
()
where
()
Notice that the derivation in (18a) and (18b) is similar to that in (17a) and (17b). The local MDP problem (18a) and (18b) can be solved by the distributed computing , which implies . As shown in (19), the probability density functions (PDFs) of the packet arrival processes are required to know a priori to evaluate the F1(k). However, the PDFs are often unavailable a priori in HSR communication systems, hence, developing an online scheduling algorithm without requiring known PDFs is necessary. Fortunately, due to the concept of opportunistically minimizing an expectation [19], an online algorithm can be developed by removing the expectation operator. Given the observed packet arrivals Ak for all services and the scheduling policy can be obtained by , where .

4.2.2. Distributed Scheduling Policy in Second Stage

By substituting the results from the first stage into (17a) and (17b), the scheduling policy in the second stage can be obtained by solving the following problem:
()
where
()
Similarly, given and , we can solve (20) by the distributed computing , which implies .

4.3. Distributed Online Scheduling Algorithm

Based on the distributed scheduling policy in two stages, we propose a distributed online scheduling algorithm using stochastic learning, which determines the scheduling actions and the per-node value functions as well as the LMs. As the train moves from the origin station to the terminal, the online algorithm allocates the network resource to multiple services slot by slot. The detailed steps of the proposed algorithm are given as follows.

Step 1 (initialization). RS initializes the value functions and LMs . Meanwhile, CSs initialize .

Step 2 (scheduling decisions). When the train is moving, each CS and RS decide the scheduling actions in the two stages separately at the beginning of slot t. After obtaining H1(t), the link capacity CBS(t) can be calculated. Then based on the local state information Ak(t), QCS,k(t), and , each CS calculates which is exchanged to determine the scheduling actions in the first stage. Similarly, using the scheduling results in the first stage, based on the local state information QR,k(t), H2(t), and , RS determines the scheduling actions in the second stage.

Step 3 (per-node value functions and LMs update). Each CS updates and the RS updates as well as the LMs according to the parameter update processes. Then let t : = t + 1 and go to Step 2 until convergence.

The parameters are updated by the subgradient method, which is described as follows:
()
()
()
where and are the step size sequences satisfying [17]: (1), , ; (2), , ; and (3). Furthermore, to enforce the convergence of the LMs and per-node value functions, and should also satisfy , for example, and .

As shown in [20], the key idea of iteration convergence is characterized as follows. In (22a), (22b), and (22c), the updates of the per-stage value functions and as well as the LMs βk are performed using different step sizes. The update rate of the value functions is faster than that of the LMs. From the perspective of the LMs, the value functions will approximately converge to the optimal values corresponding to their current values, because they are updated at a faster time scale. Also, from the perspective of the value functions, the LMs appear to be almost constant. These two time-scale updates ensure that the value functions and the LMs converge to the optimal solution.

4.4. Implementation Issues

The distributed online scheduling algorithm runs in the three steps when the train moves from the origin station to the terminal. At each decision epoch, the scheduling actions in both stages are decided after observing each local CSI and QSI. It is worth emphasizing that the proposed algorithm is different from the iterative algorithms in static optimization problems because the data packets can be delivered during the iteration steps.

As an alternative, a table look-up method can be used for service scheduling in HSR networks. Specially, once the scheduling policy is obtained by the distributed online scheduling algorithm or other algorithms it can be stored in a table format. Each entry of the table represents the scheduling action for the given global system state including CSI and QSI. At each decision epoch, after observing the current state, the network controller looks up the table to find out the corresponding scheduling action and then executes the scheduling decision. The table look-up method is effective with low computational complexity.

Furthermore, the periodic updates in the proposed algorithm are necessary. After the proposed algorithm converges, the updates can be performed with long frequency slots or at random slots instead of at every slot. Since all the channel and queue states are realized infinitely many times during the trip, the periodic updates can ensure that the proposed algorithm also converges to the optimal solution. If the table look-up method is used, the table storing the scheduling policy can also be updated corresponding to each update in the proposed algorithm.

5. Simulation Results and Discussions

In this section, we implement the proposed scheduling algorithms using MATLAB and present simulation results to illustrate the performance of the algorithm.

5.1. Simulation Setup

For the purpose of comparison, we evaluate three related scheduling schemes as reference benchmarks. The first one is the traditional round-robin (RR) scheme which schedules services in a predetermined order. At time-slot t, the (t mod⁡ (K + 1))th service is chosen for the two links. The second one is the greedy scheme, where service scheduling is done in a greedy method. Specifically, and . The third one is the heuristic packet scheduling algorithm proposed in [21] and used in the two links, where the services are scheduled for transmission depending on transmission rate, packet utility, and proportional fairness.

In order to better illustrate the performance of the scheduling algorithms, the suitable parameters should be set in simulations. We use a typical setting for HSR communication systems [10], with TB = 53 μs and G = 240 bits. The wireless communication in the two-hop link is established based on a carrier frequency of 2.4 GHz with bandwidth W1 = W2 = 10 MHz. The transmit power of the BS and AP is PBS = 47 dBm and PR = 14 dBm, respectively. The Rayleigh fading channel state HR,k(t) is sampled from the probability density function expressed as , h ≥ 0, and  dB. For the Rician fading channel state, HBS,R(t), Rician factor is 6 dB according to the Winner II project measurement results [22]. The maximum size LQ for all buffers can be set as 50 packets such that there is no packet dropped from the buffers. A single simulation runs the algorithms for 400 slots and the results are averaged over 100 simulation runs.

5.2. Simulation Results

In our proposed scheduling algorithm, the objective is to minimize the expected cost function defined in (8), which includes the e2e delay. In the simulation results, the average e2e delay and service satisfaction are used as metrics to show the performance improvement. In addition, the convergence of the proposed distributed online scheduling algorithm is established through simulations.

Figure 2 compares the delay performance of the four scheduling schemes with different numbers of requested services. We set the delivery ratio requirement αk = 0.8 for all services with an equal average packet arrival rate of 5 packets/slot. It can be observed that the proposed distributed scheduling algorithm could achieve significant performance gains in average e2e delay over the other schemes. This illustrates the advantages of the proposed algorithm with distributed scheduling policy, which could effectively reduce the value of expected cost function in the two-hop HSR networks. Furthermore, we can see that, as the number of requested services increases, the average e2e delay per service for all scheduling schemes grows. This can be explained as follows. Since the capacity of the wireless channel is fixed in general, when the number of requested services increases, there are more data packets to be transmitted and less scheduling chance will be given to a certain service; then the average e2e delay per service becomes larger. Therefore, to reduce the average delay for service delivery and satisfy the QoS requirements, multi-input multioutput (MIMO) antennas can be deployed to improve the capacity of the wireless channel in HSR communication systems.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Average e2e delay per service versus the number of services.

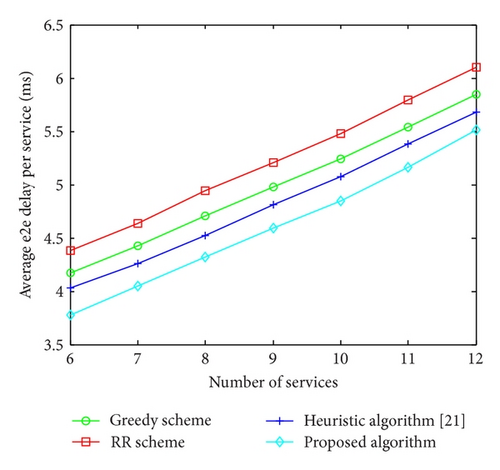
Figure 3 presents the delay performance with respect to the average packet arrival rate for the four scheduling schemes. In the simulation, there are 6 types of services supported and αk = 0.8 for each service. The average packet arrival rate for all services is set from 1 to 7 in order to prevent buffer overflow. From the figure, we can see that the average e2e delay per service in the proposed scheduling algorithm is smaller than the other schemes no matter how much the packet arrival rate is. In addition, the average delay value increases quickly with the increase of average packet arrival rate, which can be explained by Little’s law. For the video services on the train, the average packet arrival rate is very high, so it is necessary to provide a large buffer or improve wireless transmission rate so as to prevent buffer overflow.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Average e2e delay per service versus packet arrival rate.

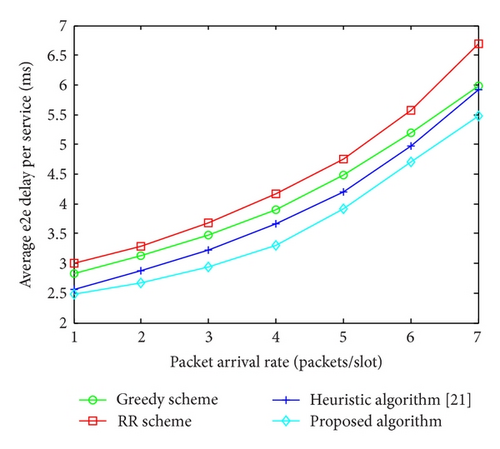
Figure 4 indicates the service delivery performance under the four scheduling schemes with K = 6 service types. The average packet arrival rates for all services are equal to 6 packets/slot. Based on the delivery ratio constraints (9), we define the satisfaction parameter εk of service k as the ratio of average throughput to αkλk; that is, . A larger εk represents the higher satisfaction of service k and εk ≥ 1 implies that the delivery ratio constraint for service k is satisfied. Let the delivery ratio requirements from service 1 to service K be 0.9, 0.9, 0.8, 0.8, 0.7, and 0.7. For service k, the rightmost bar shows the parameter εk for the proposed scheduling algorithm, and the remaining bars represent the parameter εk for the other three schemes. Simulation results show that the proposed distributed two-stage scheduling algorithm can achieve better service delivery performance over other schemes. This can be explained as follows. The RR scheme is fair in terms of scheduling opportunities but not channel/queue aware, the greedy scheme schedules the service with more packets in its buffer but does not consider the channel condition, and the heuristic scheduling algorithm is developed based on transmission rate, packet utility, and proportional fairness, which does not consider the heterogeneous delivery ratio requirements for different services. The same is true for both the two stages. Thus, the proposed algorithm, which is channel/queue aware and considers the service delivery ratio requirements, will be efficient on delivery ratio constraints in the long term.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Service delivery performance.

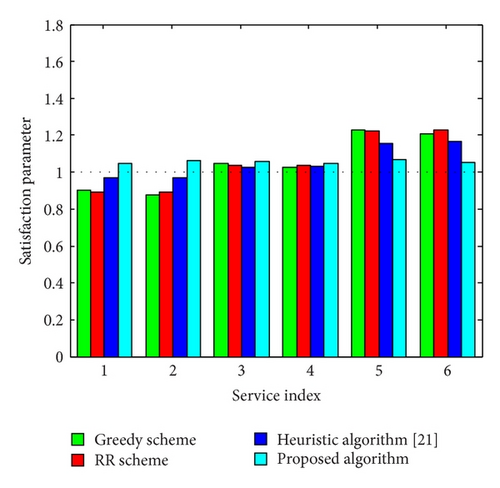
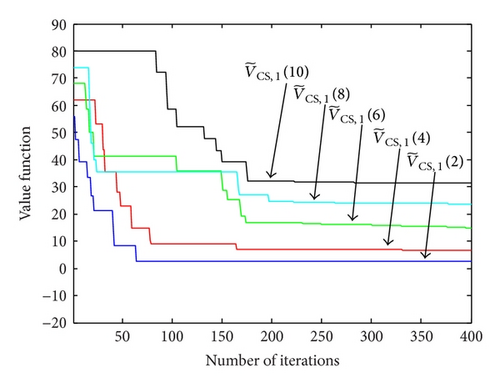
Figure 5 illustrates the convergence property of the proposed distributed online scheduling algorithm. We plot the value functions of the CS for the first type of service versus scheduling slot index. It can be seen that the distributed algorithm converges quite fast and the values are extremely close to the final converged results after 200 iterations. The similar results can be obtained for per-node value functions at other CSs and RS. By comparing different curves, we can see that the per-node value function is increasing in queue backlog q. There are two reasons to explain this property. First, the value of per-slot cost function (7) grow linearly with the increase of queue backlog q. Second, the value function is positively correlated with the per-slot cost function based on (15). Furthermore, unlike the iterations in static optimization problems, the proposed scheduling algorithm is online, implying that data packets are delivered during the iteration steps.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Illustration of the convergence of the proposed algorithm.

6. Conclusion

Providing passengers with multimedia services is one of the most important applications in HSR communication systems. This paper investigated delay-aware downlink service scheduling problem with stochastic packet arrivals and QoS requirements in relay-assisted HSR communication systems. We elaborate on the theory of MDP and illustrate how the approximate MDP and stochastic learning could help in obtaining low-complexity and distributed scheduling solutions. Simulation results show that the proposed algorithm outperforms other existing schemes in terms of average e2e delay and service delivery performances. Furthermore, the convergence of the proposed distributed online scheduling algorithm is shown by simulations.

For our future work, we will investigate the dynamic stochastic scheduling problem in the HSR networks using the stochastic network optimization approach. In addition, since the delay-aware is considered, motivated by [23], the design of a dynamic output feedback controller is necessary for multimedia services transmission in HSR communication systems.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This work is supported by the Fundamental Research Funds for the Central Universities (Grant no. 2014YJS026), the Key Projects of State Key Lab of Rail Traffic Control and Safety (nos. RCS2012ZZ004 and RCS2010ZT011), the China Postdoctoral Science Foundation (Grant no. 2013M530519), and the Natural Science Foundation of China (Grant no. U1334202).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.