Volume 2014, Issue 1 230847

Research Article

Open Access

Computing Singular Points of Projective Plane Algebraic Curves by Homotopy Continuation Methods

Zhongxuan Luo,

Corresponding Author

Zhongxuan Luo

[email protected]

School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China dlut.edu.cn

School of Software, Dalian University of Technology, Dalian 116620, China dlut.edu.cn

Search for more papers by this author

Erbao Feng,

Erbao Feng

orcid.org/0000-0001-7808-0950

School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China dlut.edu.cn

Search for more papers by this author

Jielin Zhang,

Jielin Zhang

orcid.org/0000-0001-9250-0632

School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China dlut.edu.cn

Search for more papers by this author

Zhongxuan Luo,

Corresponding Author

Zhongxuan Luo

[email protected]

School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China dlut.edu.cn

School of Software, Dalian University of Technology, Dalian 116620, China dlut.edu.cn

Search for more papers by this author

Erbao Feng,

Erbao Feng

orcid.org/0000-0001-7808-0950

School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China dlut.edu.cn

Search for more papers by this author

Jielin Zhang,

Jielin Zhang

orcid.org/0000-0001-9250-0632

School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China dlut.edu.cn

Search for more papers by this author

First published: 05 June 2014

https://doi.org/10.1155/2014/230847

Academic Editor: Baodong Zheng

Share a link

Email
Wechat
Bluesky

Abstract

We present an algorithm that computes the singular points of projective plane algebraic curves and determines their multiplicities and characters. The feasibility of the algorithm is analyzed. We prove that the algorithm has the polynomial time complexity on the degree of the algebraic curve. The algorithm involves the combined applications of homotopy continuation methods and a method of root computation of univariate polynomials. Numerical experiments show that our algorithm is feasible and efficient.

1. Introduction

Algebraic curves are a classic research object in mathematics. The related computation of algebraic curves arises in several applications, including number theoretic problems [1], ancient and modern architectural designs, error-correcting [2], biological shape [3], cryptographic algorithms [4, 5], and computer aided geometric design [6, 7]. Singular points and their multiplicities and characters play an important role in the research of algebraic curves [8]. They help to determine the genus of an algebraic curve. Singular points also show some shape features, such as nodes, self-intersections or cusps of real curves in robot motion planning, computer aided geometry design, and machine vision. And the determination of geometric shape and topology of the real curves depends on the singular points. The computation of singular points is also crucial for tracing curves algorithms [9].

As singular points of an algebraic curve are the solutions of a polynomial system, most of algorithms in [10–15] solve the polynomial system either by Gröbner basis method described in [16] or by resultant computation. These methods rely on symbolic algebraic computation that requires exact input of coefficients of algebraic curves. It is easy for them to suffer from the overwhelming coefficient swell. So these methods may be limited to relatively small problem. Furthermore, it is difficult to obtain exact coefficients of algebraic curves due to data error in many fields of science and engineering.

Although we have presented an algorithm to compute singular points of irreducible algebraic curves in [17], the algorithm is almost experimental and related analysis of the algorithm is not provided, for instance, the feasibility and complexity. The aims of this paper are analyzing the feasibility of this algorithm for computing singular points of reducible algebraic curves and proving that the algorithm has polynomial time complexity on the degree of an algebraic curve. We also present the effect of tiny perturbations of coefficients of algebraic curves on singular points and it may be a part of reasons why we compute the singular points numerically.

Our algorithm is totally numerical and can deal with algebraic curves with inexact coefficients. It includes the applications of homotopy continuation methods and the method of calculating the multiple roots of univariate polynomials with inexact coefficients without using multiprecision arithmetic. Homotopy continuation method is a reliably and efficiently numerical method to solve the polynomial systems [18]. Several methods have been presented to compute roots of univariate polynomials, such as Laguerre’s method, Jenkins-Traub method, and the QR algorithm with the companion matrix. However, they cannot overcome a barrier of attainable accuracy on an m multiple root [19, 20]. If we have k₁ digits coefficients accuracy and k₂ digits machine precision, the attainable accuracy is min⁡{k₁, k₂}/m digits. For example, if the standard double precision of 16 decimal digits is used and the accuracy of coefficients of the polynomial is 15 digits, only 3 correct digits of a root of multiplicity 5 can be obtained by the above methods. A method proposed by Zeng [21] is not subject to the accuracy barrier and a lot of numerical experiments have shown its efficiency and robustness.

The following section presents the basic notions on algebraic curves and singular points. In Section 3, we focus on the algorithm of computing singular points. Section 4 is devoted to the numerical experiments. We conclude this paper in Section 5.

2. Preliminaries

In this section, we introduce some basic notions and results on algebraic curves and singular points. Let be the complex numbers field and let be the projective plane over .

Definition 1 (see [8], [22].)A projective plane algebraic curve over is defined as the set

()

for a nonconstant square-free homogeneous polynomial

We call F(x, y, z) the defining polynomial of . The degree of polynomial F(x, y, z) is called the degree of .

We take the line z = 0 in

as the line at infinity. If the projective plane algebraic curve

is defined by the polynomial F(x, y, z), then the corresponding affine plane algebraic curve

is defined by the dehomogenization f(x, y) of F(x, y, z),

()

where

is the affine plane over

Therefore, if

()

then

()

where f_k(x, y) is a homogeneous polynomial of degree k and f_n(x, y) is nonzero.

Throughout this paper, whenever we speak of a “curve” we mean an “algebraic curve.” For brevity, we will usually use the phrase “the curve F(x, y, z) = 0” instead of “the projective plane algebraic curve whose defining polynomial is F(x, y, z).” Of course, a polynomial G = cF, for some nonzero , defines the same curve, so F is unique only up to multiplication by nonzero constants. The above usage is also for the case of affine plane algebraic curve.

Every point (a, b) on corresponds to a point (a : b : 1) on , and every additional point on is a point at infinity. In other words, the first two coordinates of additional points are the nontrivial solutions of f_n(x, y) = 0, with the third coordinates being 0. Thus, the curve has only finitely many points at infinity.

Definition 2 (see [8], [22].)Let be an affine plane algebraic curve over defined by , and let . P is of multiplicity r on if and only if all derivatives of f(x, y) up to and including the (r − 1)th vanish at P, but at least one rth derivative does not vanish at P.

A point of multiplicity two or more is said to be a singular point, and especially the point of multiplicity two is called a double point. A point of multiplicity one is called a simple point.

It is evident that a necessary and sufficient condition that a point (a, b) of the curve f(x, y) = 0 is singular is that

()

Definition 3 (see [8].)Let the parametric equations of tangents to the curve f(x, y) = 0 at P = (a, b) be

()

and the tangents to the curve f(x, y) = 0 at P = (a, b) of multiplicity r are determined by the ratio λ : μ and correspond to the roots of

()

where

, and they are counted with multiplicities equal to the multiplicities of the corresponding roots of this equation.

Definition 4 (see [8], [22].)A singular point P of multiplicity r on an affine plane algebraic curve is called ordinary if and only if the r tangents to at P are distinct and nonordinary otherwise. The property of singular point P of being ordinary or nonordinary is called the character of P.

The criteria for the multiplicity of a point on the projective plane algebraic curve can be characterized as follows.

Proposition 5 (see [8].) is a point of multiplicity r on the projective plane algebraic curve F(x, y, z) = 0 if and only if all the (r − 1)th derivatives of F(x, y, z), but not all the rth derivatives, vanish at Q.

As a corollary of this proposition, a point Q of the curve F(x, y, z) = 0 being singular can be put in a more convenient form.

Proposition 6 (see [8], [22].) is a singular point of the projective plane algebraic curve F(x, y, z) = 0 if and only if

()

The following two theorems are of use for analyzing the algorithm of the next section.

Theorem 7 (see [8].)If a curve of degree n with no multiple components has multiplicities r_i at points P_i, then

()

Theorem 8 (see [8] Bézout’s theorem.)Two curves of degrees m and n with no common components have exactly mn intersections.

3. Computation of Singular Points

In this section, a method of solving the overdetermined polynomial systems is presented first. We also outline the algorithm on computing the singular points of projective plane algebraic curves, and afterwards we analyze feasibility and complexity of the algorithm. The last subsection includes the effect of tiny perturbations of coefficients of the curve on singular points.

3.1. Solving Overdetermined Polynomial Systems

The following proposition shows how to reduce an overdetermined polynomial system to a square system that most of the papers and software programs on homotopy continuation method focus on. Let n and N be the number of equations and unknowns, respectively, and n > N.

Proposition 9 (see [23], [24].)There are nonempty Zariski open dense sets of parameters or such that every isolated solution of

()

is an isolated solution of

()

The solutions set of an overdetermined system belongs to that of the corresponding square system, but the converse is not true.

3.2. Algorithm

We summarize the algorithm described in [17] for computing the singular points of irreducible projective plane algebraic curves.

Algorithm 1. Input. Consider projective plane algebraic curve F(x, y, z) = 0 and corresponding affine plane algebraic curve f(x, y) = 0. Threshold is ϵ > 0.

Output. Consider singular points and their multiplicities and characters of the curve F(x, y, z) = 0.

Step 1 (randomization). By Proposition 9 and choosing the random complex numbers α and β, we add random multiples of the last equation to the first two equations of the polynomial system (5):

()

Step 2 (computing the singular points (a : b : 1)). We solve the polynomial system (12) by the polyhedral homotopy continuation method first and denote the solutions set as {(a : b : 1)}. If |f(a, b)| < ϵ, (a : b : 1) will be a singular point.

Step 3 (computing the singular points (a : b : 0) at infinity). Since f_n(x, y) is a bivariate homogeneous polynomial of degree n, we obtain the points set {(a : b : 0)} at infinity by solving the corresponding univariate polynomial. By Proposition 6, if Max⁡{(∂F/∂x)(a, b, 0), (∂F/∂y)(a, b, 0), (∂F/∂z)(a, b, 0)} < ϵ, then (a : b : 0) will be a singular point at infinity.

When we determined the multiplicity and character of singular point (a : b : 0) at infinity, (a : b : 0) will be transferred to point (a^′ : b^′ : 1) by simple linear transformation.

Step 4 (determining the multiplicity). Evaluating the derivatives of f(x, y) at a singular point from order equal to 2, if the moduli of all derivatives of f(x, y) up to and including the (r − 1)th are less than ϵ, but at least one modulus of rth derivatives is greater than ϵ, then the multiplicity of this singular point will be determined as r.

Step 5 (determining the character). The tangents to the curve f(x, y) = 0 at a singular point of multiplicity r correspond to the roots of (7). Whether the singular point is ordinary or not will be determined if there are multiple roots of (7).

3.3. Remarks on Feasibility of Algorithm

The following theorems and remarks will show the feasibility of Algorithm 1 for computing the singular points of reducible projective plane algebraic curves.

Theorem 10. All the solutions of polynomial system (12) are isolated.

Proof. Since f(x, y) is square-free, f(x, y) and f_x(x, y) have no nonconstant common divisors. It also holds for f(x, y) and f_y(x, y). In Step 1 of Algorithm 1, for the random complex numbers α and β, f(x, y) + αf_y(x, y) and f_x(x, y) + βf_y(x, y) also have no nonconstant common divisors. It follows that all the solutions of polynomial system (12) are isolated.

Remark 11. The inequality in Theorem 7 shows that an irreducible curve has finitely many singular points. So, the singular point of an irreducible curve is isolated.

Theorem 12. A reducible curve f(x, y) = 0 has only finitely many singular points and they are all isolated points.

Proof. Without loss of generality, we may assume that f(x, y) = f₁(x, y)f₂(x, y), where f₁(x, y) and f₂(x, y) are irreducible polynomials. Obviously, the singular points of f(x, y) = 0 are the singular points of f_i(x, y) = 0 (i = 1,2) and the intersections of f₁(x, y) = 0 and f₂(x, y) = 0. By Remark 11 and Theorem 8, the set of singular points of f(x, y) = 0 is finite and the singular points are all isolated.

Remark 13. When solving the polynomial system (12) in Step 2 of Algorithm 1 by homotopy continuation methods, Proposition 9 and Theorem 12 imply that all singular points (a : b : 1) of reducible curve can be determined.

Remark 14. In Step 2 of Algorithm 1, the Jacobian of polynomial system (12) is

()

This matrix is singular at a singular point of multiplicity three at least. The numerical techniques of homotopy continuation methods could deal with this well.

Remark 15. As f(x, y) is a nonzero polynomial and has finite degree n, the modulus of some derivative of order less than or equal to n must be greater than the given threshold at a singular point. Hence, Step 4 of Algorithm 1 ends for determining the multiplicities of finitely many singular points.

Remark 16. We solve univariate polynomials in Steps 3 and 5 of Algorithm 1. Numerical singular points make the coefficients of univariate polynomials in Step 5 inexact. We have mentioned the efficiency of computation of multiple roots of inexact univariate polynomials proposed by Zeng in Section 1. Employing Zeng’s method, we compute the singular points at infinity accurately in Step 3 and the characters of all singular points can be determined correctly in Step 5.

3.4. Computational Complexity

In this subsection, we analyze the computational complexity of Algorithm 1. The degree of the curve f(x, y) = 0 is denoted by n.

Theorem 17. The complexity of Step 2 in Algorithm 1 is O(n²).

Proof. Shub and Smale [25, 26] present that finding an approximate zero of a polynomial system by homotopy continuation methods can be solved in polynomial time on the average and the number of arithmetic operations is bounded by cN⁴, where c is a universal constant and N is the number of variables. By Bézout’s Theorem 8, the number of solutions of polynomial system (12) is n(n − 1) at most. We deduce that the complexity of Step 2 is no more than 16cn(n − 1).

Theorem 18. The complexity of Steps 3 and 5 in Algorithm 1 is O(n³) and O(n⁵) or less, respectively.

Proof. Pan reports [19] that the complexity of general root-finders of univariate polynomial of degree d is O(d²) or less, but Zeng’s method [21] reaches high accuracy on multiple roots at the higher computing cost of O(d³). It follows that the complexity of Step 3 is O(n³). From Steps 2 and 3, we know that the number of singular points of the curve f(x, y) = 0 of degree n is n² at most. Therefore, we conclude that the complexity of Step 5 is O(n⁵) or less.

Theorem 19. The complexity of Step 4 in Algorithm 1 does not exceed O(n⁵).

Proof. The number of all the nonzero derivatives of bivariate polynomial f(x, y) of degree n is not more than n(n + 3)/2. The complexity of evaluation of a polynomial at a point is linear in the degree of the polynomial and the number of variables. Since there are n² points at most in Step 4 of Algorithm 1 and the complexity of linear change of coordinates is polynomial in the number of variables, the complexity of Step 4 does not exceed O(n⁵).

The following theorem holds at once.

Theorem 20. The complexity of Algorithm 1 is polynomial time in the degree n of the projective plane algebraic curve and is O(n⁵).

3.5. Effect of Tiny Perturbations on Singular Points

The authors [27] conclude that random perturbations of coefficients of plane algebraic curves will almost invariably destroy all singular points. The current methods dealing with plane algebraic curves are almost ill-conditioned with respect to tiny perturbations. For example, let us consider the curve x³ − y² = 0 with nonordinary double singular point (0,0) and its perturbation x³ − y² + ϵx² = 0, where ϵ > 0. It is natural to compute the approximate singular point out and the original character for relative magnitude ϵ > 0. However, the character of singular point (0,0) is changed by using symbolic algebraic computation, even if ϵ > 0 is sufficiently small.

For the curve x³ − y² + ϵx² = 0, when ϵ = 0.0000001, the numerical procedure based on Algorithm 1 outputs a nonordinary double singular point

()

4. Numerical Experiments

In this section, Algorithm 1 is implemented in Matlab and some examples are presented to show the efficiency of corresponding numerical procedure. There are many freely available homotopy continuation packages. As Lee et al. [28] report that HOM4PS-2.0 is generally the fastest package for solving small to moderately large sparse systems, it is employed to solve polynomial system (12) in Algorithm 1. Many numerical examples are provided in [17] where the curves are irreducible and the coefficients of the curves are inexact. We finish this section with two reducible curves.

Example 1. Consider

()

There are two components f₁(x, y) = 0 and f₂(x, y) = 0 for the curve f(x, y) = 0. The curve f₁(x, y) = 0 has no singular points and its real part is plotted in Figure 1. The curve f₂(x, y) = 0 has nonordinary double singular point corresponding to (0 : 0 : 1) and ordinary double singular point corresponding to (0 : 1 : 0). Figure 2 shows real part of the curve f₂(x, y) = 0 and the singular point corresponding to (0 : 0 : 1) is marked by a solid square.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Real part of f₁(x, y) = 0 in Example 1.

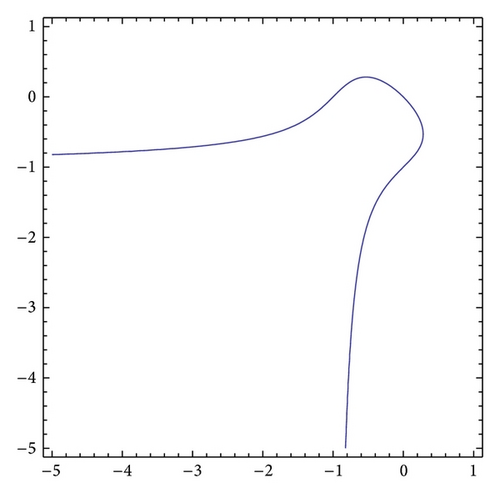
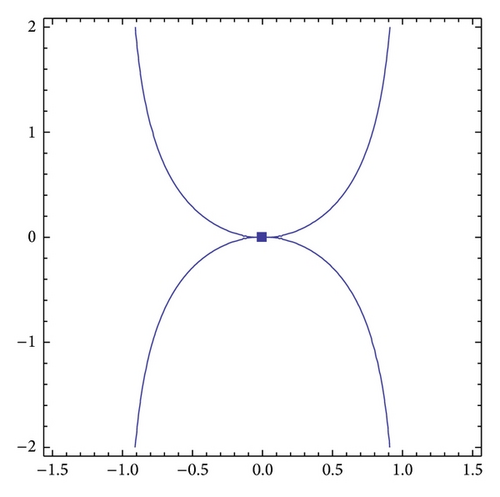
The curves f₁(x, y) = 0 and f₂(x, y) = 0 have 8 intersections corresponding to Q_i (i = 1, …, 8). Their related projective curves intersect Q₉ = (0,1, 0) at infinity. (0,0) is the simple point of f₁(x, y) = 0, nonordinary double point of f₂(x, y) = 0. Therefore, (0,0) corresponding to Q₁ = (0 : 0 : 1) is nonordinary singular point of multiplicity of 3 of f(x, y) = 0. Q₉ = (0 : 1 : 0) is ordinary double point and simple point of the corresponding projective curves for f₂(x, y) = 0 and f₁(x, y) = 0, respectively. The tangent to the latter at Q₉ coincides with one tangent to the former at Q₉. So, Q₉ = (0 : 1 : 0) is nonordinary singular point of multiplicity of 3 of the projective curve corresponding to f(x, y) = 0.

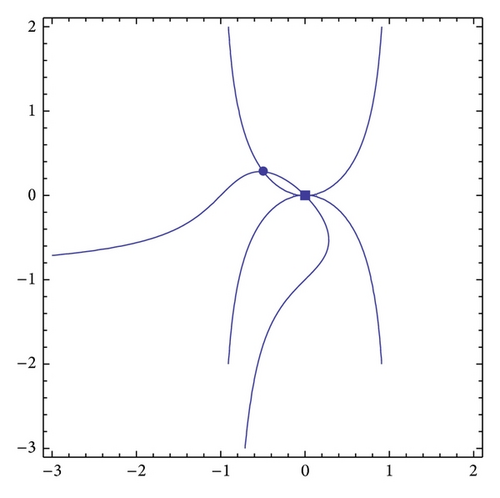
Table 1 lists the results of our numerical procedure for the projective curve corresponding to f(x, y) = 0 in Example 1. Figure 3 presents the real part of f(x, y) = 0 in Example 1. The solid dot marks the real intersection of f₁(x, y) = 0 and f₂(x, y) = 0 corresponding to Q₅. The real singular point corresponding to Q₁ = (0 : 0 : 1) is still marked by a solid square.

Table 1. Results for f(x, y) = 0 in Example 1.

	x	y	z	Mult.	Ord.
Q₁	0.00000003 + 0.00000005i	0.00000000 + 0.00000000i	1.00000000	3	No
Q₂	−0.89868027 + 0.41873939i	−0.15046254 + 1.06341745i	1.00000000	2	Yes
Q₃	0.36804326 − 1.20320368i	−0.92239819 − 0.40178011i	1.00000000	2	Yes
Q₄	0.36804326 + 1.20320368i	−0.92239819 + 0.40178011i	1.00000000	2	Yes
Q₅	−0.49367385 − 0.00000000i	0.28024456 + 0.00000000i	1.00000000	2	Yes
Q₆	−0.89868027 − 0.41873939i	−0.15046254 − 1.06341745i	1.00000000	2	Yes
Q₇	0.77747393 + 0.21532054i	−0.56726154 − 0.66500198i	1.00000000	2	Yes
Q₈	0.77747393 − 0.21532054i	−0.56726154 + 0.66500198i	1.00000000	2	Yes
Q₉	0.00000000	1.00000000	0	3	No

We use the abbreviations “Mult.” and “Ord.” for the words “multiplicity” and “ordinary” in our tables, respectively.

Example 2. Consider

()

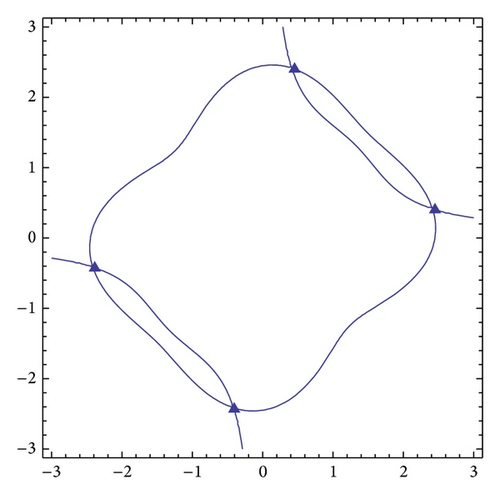
The curve f(x, y) = 0 has two components f₁(x, y) = 0 and f₂(x, y) = 0. There are six singular points corresponding to P_i (i = 1, …, 6) for the curve f₁(x, y) = 0 and they are marked by solid squares in Figure 4 where the real part of the curve f₁(x, y) = 0 is plotted. Four singular points corresponding to P_i (i = 7, …, 10) of the curve f₂(x, y) = 0 are illustrated by the solid triangles in Figure 5 where the real part of the curve f₂(x, y) = 0 is presented. Obviously, P_i (i = 1, …, 10) are singular points of the projective curve corresponding to the curve f(x, y) = 0.

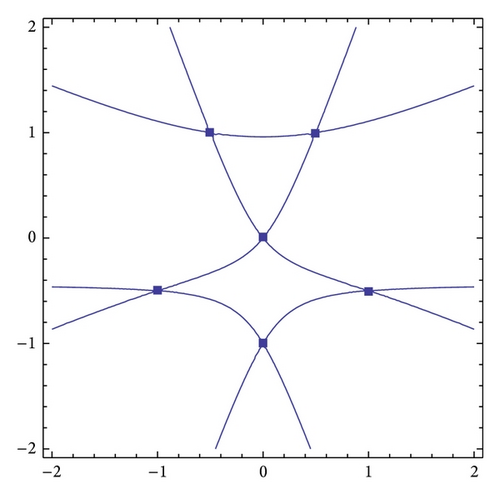
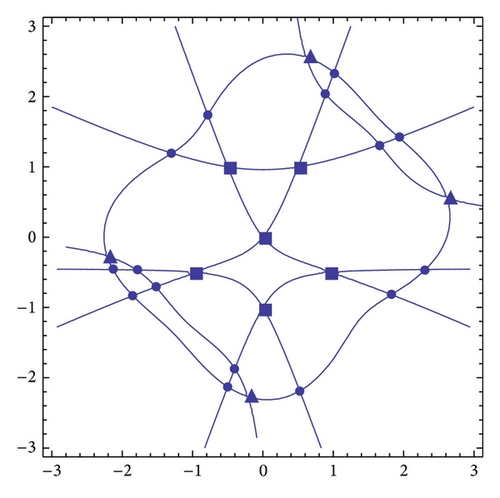
There are 29 intersections corresponding to P_i (i = 11, …, 39) for the curves f₁(x, y) = 0 and f₂(x, y) = 0. Their related projective curves intersect P₄₀ at infinity. These 30 intersections P_i (i = 11, …, 40) are also singular points of the projective curve corresponding to the curve f(x, y) = 0. So the curve f(x, y) = 0 has 40 singular points.

Figure 6 shows the real part of the curve f(x, y) = 0 whose real singular points are marked by the solid dots, squares, and triangles. The solid dots mark the real intersections of the curves f₁(x, y) = 0 and f₂(x, y) = 0. The solid squares and triangles illustrate the singular points of the curves f₁(x, y) = 0 and f₂(x, y) = 0, respectively. Table 2 lists the results of our numerical procedure for the projective curve corresponding to f(x, y) = 0 in Example 2.

Table 2. Results for f(x, y) = 0 in Example 2.

	x	y	z	Mult.	Ord.
P₁	0.00000000	0.00000000 − 0.00000000i	1.00000000	2	Yes
P₂	−0.50000000 − 0.00000000i	0.99999999 + 0.00000000i	1.00000000	2	Yes
P₃	−0.00000000 − 0.00000000i	−1.00000000 + 0.00000000i	1.00000000	2	Yes
P₄	0.99999999 + 0.00000000i	−0.50000000 − 0.00000000i	1.00000000	2	Yes
P₅	−1.00000000 + 0.00000000i	−0.50000000 + 0.00000000i	1.00000000	2	Yes
P₆	0.50000000 + 0.00000000i	1.00000000 + 0.00000000i	1.00000000	2	Yes
P₇	2.41421356 − 0.00000000i	0.41421356 − 0.00000000i	1.00000000	2	Yes
P₈	−2.41421356 + 0.00000000i	−0.41421356 − 0.00000000i	1.00000000	2	Yes
P₉	0.41421356 − 0.00000000i	2.41421356 − 0.00000000i	1.00000000	2	Yes
P₁₀	−0.41421356 − 0.00000000i	−2.41421356 + 0.00000000i	1.00000000	2	Yes
P₁₁	1.86368244 + 0.00000000i	−0.81167781 + 0.00000000i	1.00000000	2	Yes
P₁₂	−0.56599742 + 0.66867689i	0.95095432 − 0.12549545i	1.00000000	2	Yes
P₁₃	−0.58308154 + 0.00000000i	−2.34385106 + 0.00000000i	1.00000000	2	Yes
P₁₄	1.67570344 + 0.00000000i	1.32326562 + 0.00000000i	1.00000000	2	Yes
P₁₅	0.79829233	1.77539598 + 0.00000000i	1.00000000	2	Yes
P₁₆	0.09549542 − 0.39009016i	−0.97196258 + 0.89462218i	1.00000000	2	Yes
P₁₇	0.52445070 + 0.00000000i	−2.19040368 − 0.00000000i	1.00000000	2	Yes
P₁₈	0.05975897 − 0.25434442i	−0.06366391 − 0.36672723i	1.00000000	2	Yes
P₁₉	0.15502368 − 1.39689139i	−0.01303583 + 0.19325672i	1.00000000	2	Yes
P₂₀	0.51269502 + 0.43085324i	−0.51116222 + 0.08768075i	1.00000000	2	Yes
P₂₁	0.15502368 + 1.39689139i	−0.01303583 − 0.19325672i	1.00000000	2	Yes
P₂₂	0.09549542 + 0.39009016i	−0.97196258 − 0.89462218i	1.00000000	2	Yes
P₂₃	0.54660137 + 0.59723958i	−0.36484540 − 0.17346068i	1.00000000	2	Yes
P₂₄	1.40455064 + 0.00000000i	1.22984070 + 0.00000000i	1.00000000	2	Yes
P₂₅	−2.11390876 − 0.00000000i	−0.91044961 − 0.00000000i	1.00000000	2	Yes
P₂₆	−2.39860964 + 0.00000000i	−0.45929305 − 0.00000000i	1.00000000	2	Yes
P₂₇	−0.35998047 + 0.25179313i	0.61198862 − 0.60194230i	1.00000000	2	Yes
P₂₈	−1.29601698 − 0.00000000i	1.19480441 + 0.00000000i	1.00000000	2	Yes
P₂₉	0.05975897 + 0.25434442i	−0.06366391 + 0.36672723i	1.00000000	2	Yes
P₃₀	−0.51418694 − 0.00000000i	−2.16372657 − 0.00000000i	1.00000000	2	Yes
P₃₁	−1.79027097 + 0.00000000i	−0.78332475 − 0.00000000i	1.00000000	2	Yes
P₃₂	−0.82449210 + 0.00000000i	1.84542750 + 0.00000000i	1.00000000	2	Yes
P₃₃	−0.35998047 − 0.25179313i	0.61198862 + 0.60194230i	1.00000000	2	Yes
P₃₄	−2.28499755 − 0.00000000i	−0.46036727 + 0.00000000i	1.00000000	2	Yes
P₃₅	2.24284114 − 0.00000000i	−0.46080446 − 0.00000000i	1.00000000	2	Yes
P₃₆	0.92084852 + 0.00000000i	2.10459508 + 0.00000000i	1.00000000	2	Yes
P₃₇	−0.56599742 − 0.66867689i	0.95095432 + 0.12549545i	1.00000000	2	Yes
P₃₈	0.54660137 − 0.59723958i	−0.36484540 + 0.17346068i	1.00000000	2	Yes
P₃₉	0.51269502 − 0.43085324i	−0.51116222 − 0.08768075i	1.00000000	2	Yes
P₄₀	1.00000000	0.00000000	0.00000000	2	Yes

It takes 0.28628 seconds and 1.26786 seconds for our numerical procedure to obtain the results of Examples 1 and 2, respectively, on the Lenovo PC with Pentium Dual Core, CPU of 2.5 GHZ, and memory of 1.99 GB. We usually choose 10⁻⁶ as the thresholds in Steps 2, 3, and 4 in Algorithm 1.

5. Conclusions

This paper provides an effective algorithm for computing the singular points of projective plane algebraic curves by homotopy continuation methods. The determination of multiplicities relies on the accuracy of singular points. The characters of singular points are determined by Zeng’s method for computing multiplicities of roots of inexact univariate polynomials. The precision of coefficients of inexact univariate polynomials in our algorithm depends on the accuracy of singular points. Several numerical examples are presented to illustrate the efficiency of our algorithm. We will discuss the adaptive thresholds of the algorithm in the future.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

This paper is supported by the National Natural Science Foundation of China (no. 11171052).

References

1 Poulakis D. and Voskos E., Solving genus zero Diophantine equations with at most two infinite valuations, Journal of Symbolic Computation. (2002) 33, no. 4, 479–491, https://doi.org/10.1006/jsco.2001.0515, MR1890582, ZBL0998.11014.
10.1006/jsco.2001.0515
Web of Science® Google Scholar
2 Pretzel O., Codes and Algebraic Curves, 1998, 8, Oxford University Press, MR1686448.
10.1093/oso/9780198500391.001.0001
Google Scholar
3 Bajaj C., Lee H., Merkert R., and Pascucci V., C. Hoffmann and W. Bronsvort, NURBS based B-rep models from macromolecules and their properties, Proceedings of 4rth Symposium on Solid Modeling and Applications, 1997, Atlanta, Ga, USA, ACM Press, 217–228.
Google Scholar
4 Buchmann J. A., Introduction to Cryptography, 2001, Springer, https://doi.org/10.1007/978-1-4684-0496-8, MR1802638.
10.1007/978-1-4684-0496-8
Google Scholar
5 Koblitz N., Good and bad uses of elliptic curves in cryptography, Moscow Mathematical Journal. (2002) 2, no. 4, 693–715, MR1986087, ZBL1063.11051.
10.17323/1609-4514-2002-2-4-693-715
Web of Science® Google Scholar
6 Sederberg T. W., Applications to computer aided geometric design, 53, Proceedings of Symposia in Applied Mathematics. Applications of Computational Algebraic Geometry, 1998, 67–89.
Google Scholar
7 Farin G., Hoschek J., and Kim M. S., Handbook of Computer Aided Geometric Design, 2002, North Holland.
10.1016/B978-044451104-1/50002-2
Google Scholar
8 Walker R. J., Algebraic Curves, 1978, Springer, New York, NY, USA, MR513824.
10.1007/978-1-4612-6323-4
Google Scholar
9 Bajaj C. L., Hoffmann C. M., Lynch R. E., and Hopcroft J. E. H., Tracing surface intersections, Computer Aided Geometric Design. (1988) 5, no. 4, 285–307, https://doi.org/10.1016/0167-8396(88)90010-6, MR983464, ZBL0659.65012.
10.1016/0167-8396(88)90010-6
Google Scholar
10 Sederberg T. W., Anderson D. C., and Goldman R. N., Implicit representation of parametric curves and surfaces, Computer Vision, Graphics, and Image Processing. (1984) 28, 72–84.
10.1016/0734-189X(84)90140-3
Web of Science® Google Scholar
11 Abhyankar S. S. and Bajaj C. L., Automatic parameterization of rational curves and surfaces—III. Algebraic plane curves, Computer Aided Geometric Design. (1988) 5, no. 4, 309–321, https://doi.org/10.1016/0167-8396(88)90011-8, MR983465, ZBL0655.65019.
10.1016/0167-8396(88)90011-8
Google Scholar
12 Sendra J. R. and Winkler F., Symbolic parametrization of curves, Journal of Symbolic Computation. (1991) 12, no. 6, 607–631, https://doi.org/10.1016/S0747-7171(08)80144-7, MR1141543, ZBL0759.14044.
10.1016/S0747-7171(08)80144-7
Web of Science® Google Scholar
13 Cox D., Curves, surfaces, and syzygies, topics in algebraic geometry and geometric modeling, Contemporary Mathematics. (2003) 334, 131–149.
10.1090/conm/334/05979
Google Scholar
14 Sun Y. and Yu J., Implicitization of parametric curves via Lagrange interpolation, Computing. (2006) 77, no. 4, 379–386, https://doi.org/10.1007/s00607-006-0163-5, MR2244948, ZBL1118.14063.
10.1007/s00607-006-0163-5
Web of Science® Google Scholar
15 Sakkalis T. and Farouki R., Singular points of algebraic curves, Journal of Symbolic Computation. (1990) 9, no. 4, 405–421, https://doi.org/10.1016/S0747-7171(08)80019-3, MR1056634, ZBL0699.14035.
10.1016/S0747-7171(08)80019-3
Web of Science® Google Scholar
16 Cox D., Little J., and O′Shea D., Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra, 1997, 2nd edition, Springer, New York, NY, USA, MR1417938.
Google Scholar
17 Luo Z.-x., Feng E.-b., and Hu W.-y., Computing numerical singular points of plane algebraic curves, Communications in Mathematical Research. (2012) 28, no. 2, 146–158, MR3027499, ZBL1265.65027.
Google Scholar
18 Li T. Y., Numerical solution of polynomial systems by homotopy continuation methods, Handbook of Numerical Analysis, 2003, 11, North-Holland, Amsterdam, The Netherlands, 209–304, MR2009773, ZBL1059.65046.
Google Scholar
19 Pan V. Y., Solving a polynomial equation: some history and recent progress, SIAM Review. (1997) 39, no. 2, 187–220, https://doi.org/10.1137/S0036144595288554, MR1453318, ZBL0873.65050.
10.1137/S0036144595288554
Web of Science® Google Scholar
20 Igarashi M. and Ypma T., Relationships between order and efficiency of a class of methods for multiple zeros of polynomials, Journal of Computational and Applied Mathematics. (1995) 60, no. 1-2, 101–113, https://doi.org/10.1016/0377-0427(94)00086-G, MR1354650, ZBL0837.65048.
10.1016/0377-0427(94)00086-G
Web of Science® Google Scholar
21 Zeng Z., Computing multiple roots of inexact polynomials, Mathematics of Computation. (2005) 74, no. 250, 869–903, https://doi.org/10.1090/S0025-5718-04-01692-8, MR2114653, ZBL1079.12007.
10.1090/S0025-5718-04-01692-8
Web of Science® Google Scholar
22 Sendra J. R., Winkler F., and Pérez-Díazs S., Rational Algebraic Cueves, 2008, Springer, Berlin, Germany.
10.1007/978-3-540-73725-4
Google Scholar
23 Sommese A. J. and Wampler C. W., J. Renegar, M. Shub, and S. Smale, Numerical algebraic geometry, The Mathematics of Numerical Analysis (), 1996, 32, American Mathematical Society, Park City, Utah, USA, 749–763, Lectures in Applied Mathematics, MR1421365, ZBL0856.65054.
Google Scholar
24 Morgan A. P. and Sommese A. J., Coefficient-parameter polynomial continuation, Applied Mathematics and Computation. (1989) 29, no. 2, 123–160, https://doi.org/10.1016/0096-3003(89)90099-4, MR977815, ZBL0664.65049.
10.1016/0096-3003(89)90099-4
Web of Science® Google Scholar
25 Shub M. and Smale S., Complexity of Bezout′s theorem—V. Polynomial time, Theoretical Computer Science. (1994) 133, no. 1, 141–164, https://doi.org/10.1016/0304-3975(94)90122-8, MR1294430, ZBL0846.65022.
10.1016/0304-3975(94)90122-8
Web of Science® Google Scholar
26 Shub M., Complexity of Bezout′s theorem—VI. Geodesics in the condition (number) metric, Foundations of Computational Mathematics. (2009) 9, no. 2, 171–178, https://doi.org/10.1007/s10208-007-9017-6, MR2496558, ZBL1175.65060.
10.1007/s10208-007-9017-6
Web of Science® Google Scholar
27 Farouki R. T. and Rajan V. T., On the numerical condition of algebraic curves and surfaces—I. Implicit equations, Computer Aided Geometric Design. (1988) 5, no. 3, 215–252, https://doi.org/10.1016/0167-8396(88)90005-2, MR959606, ZBL0709.65011.
10.1016/0167-8396(88)90005-2
Google Scholar
28 Lee T. L., Li T. Y., and Tsai C. H., HOM4PS-2.0: a software package for solving polynomial systems by the polyhedral homotopy continuation method, Computing. Archives for Scientific Computing. (2008) 83, no. 2-3, 109–133, https://doi.org/10.1007/s00607-008-0015-6, MR2457354, ZBL1167.65366.
10.1007/s00607-008-0015-6
Google Scholar

All articles

Computing Singular Points of Projective Plane Algebraic Curves by Homotopy Continuation Methods

Abstract

1. Introduction

2. Preliminaries

3. Computation of Singular Points