Journal of Computational Methods in Physics

Volume 2014, Issue 1 207916

Research Article

Open Access

Tau-Path Following Method for Solving the Riccati Equation with Fractional Order

Muhammed I. Syam,

Corresponding Author

Muhammed I. Syam

[email protected]

Department of Mathematical Sciences, United Arab Emirates University, Al Ain 15551, United Arab Emirates uaeu.ac.ae

Search for more papers by this author

Hani I. Siyyam,

Hani I. Siyyam

Department of Mathematics, Taibah University, Al Madinah, Saudi Arabia taibahu.edu.sa

Search for more papers by this author

Ibrahim Al-Subaihi,

Ibrahim Al-Subaihi

Department of Mathematics, Taibah University, Al Madinah, Saudi Arabia taibahu.edu.sa

Search for more papers by this author

Muhammed I. Syam,

Corresponding Author

Muhammed I. Syam

[email protected]

Department of Mathematical Sciences, United Arab Emirates University, Al Ain 15551, United Arab Emirates uaeu.ac.ae

Search for more papers by this author

Hani I. Siyyam,

Hani I. Siyyam

Department of Mathematics, Taibah University, Al Madinah, Saudi Arabia taibahu.edu.sa

Search for more papers by this author

Ibrahim Al-Subaihi,

Ibrahim Al-Subaihi

Department of Mathematics, Taibah University, Al Madinah, Saudi Arabia taibahu.edu.sa

Search for more papers by this author

First published: 05 March 2014

https://doi.org/10.1155/2014/207916

Citations: 13

Academic Editor: Marta B. Rosales

Share a link

Email
Wechat
Bluesky

Abstract

A formulation for the fractional Legendre functions is constructed to find the solution of the fractional Riccati equation. The fractional derivative is described in the Caputo sense. The method is based on the Tau Legendre and path following methods. Theoretical and numerical results are presented. Analysis for the presented method is given.

1. Introduction

Recently, many papers on fractional boundary value problems have been studied extensively. Several forms of them have been proposed in standard models, and there has been significant interest in developing numerical schemes for their solutions. Several numerical techniques are used to solve such problems such as Laplace and Fourier transforms [1, 2], Adomian decomposition and variational iteration methods [3, 4], eigenvector expansion [5], differential transform and finite differences methods [6, 7], power series method [8], collocation method [9], and wavelet method [10, 11]. Many applications of fractional calculus on various branches of science such as engineering, physics, and economics can be found in [12, 13]. Considerable attention has been given to the theory of fractional ordinary differential equations and integral equations [14, 15]. Additionally, the existence of solutions of ordinary and fractional boundary value problems using monotone iterative sequences has been investigated by several authors [16–20].

We consider the Riccati equation with fractional orders of the form

()

where a, b, c, and g are continuous functions on [0,1] and y_ini is a constant.

Riccati equation with fractional order has been discussed by many researchers using different techniques such as collocation method based on Muntz polynomials [21], homotopy perturbation method [22], and series solution method [23].

In this paper we study the Tau-path following method for solving the Riccati equation with fractional order. We organize this paper as follows. In Section 2, we present basic definitions and results of fractional derivatives. We extend basic results to path following method for the fractional case. In Section 3, we introduce the fractional-order Legendre Tau method with path following method for solving the Riccati equation with fractional order. In Section 4, we present some numerical results to illustrate the efficiency of the presented method. Finally, we conclude with some comments in the last section.

2. Preliminaries

In this section, we review the definition and some preliminary results of the Caputo fractional derivatives, as well as, the definition of the fractional-order Legendre functions and their properties.

Definition 1. The Riemann-Liouville fractional integral operator I^α of order α > 0 on the usual Lebesgue space L₁[0,1] is given by

()

where

is the Euler Gamma function, see [12, 24].

For any f ∈ L₁[0,1], α, β⩾0, and γ > −1, the following properties hold:

(1)
I^α exists for any x ∈ [0,1],
(2)
I^αI^β = I^α+β,
(3)
I^αI^β = I^βI^α,
(4)
I^αx^γ = (Γ(γ + 1)/Γ(α + γ + 1))x^α+γ.

Definition 2. The Caputo fractional derivative of order α is defined by

()

provided that the integral exists, where n = [α] + 1 and [α] is the integer part of the positive real number α, x > 0.

The Caputo fractional derivative satisfies the following properties for f ∈ L₁[0,1] and α, β⩾0:

(1)
D^αI^αf(x) = f(x),
(2)
,
(3)
D^αD^βf(x) = D^βD^αf(x) = D^α+βf(x), x > 0,
(4)
D^αc = 0, where c is constant,
(5)
,
(6)
, where c₁, c₂, …, c_m are constants.

The basic concept of this paper is the Legendre polynomials. For this reason, we study some of their properties.

Definition 3. The Legendre polynomials {ℒ_k(x) : k = 0,1, 2, …} are the eigenfunctions of the Sturm-Liouville problem

()

Among the properties of the Legendre polynomials we list the following properties:

(1)
, where ,
(2)
ℒ_i+1(x) = ((2i + 1)/(i + 1))xℒ_i(x)−(i/(i + 1))ℒ_i−1(x), for i⩾1,
(3)
ℒ_i(±1) = (±1) ⁱ.

In order to use these polynomials on the interval [0,1], we define the shifted Legendre polynomials by S_i(z) = ℒ_i(2z − 1). Using the change of variable x = 2z − 1, S_i(z) has the following properties:

(1)
,
(2)
S_i+1(z) = ((2i + 1)/(i + 1))(2z − 1)S_i(z)−(i/(i + 1))S_i−1(z), for i⩾1,
(3)
S_i(0) = (−1) ⁱ and S_i(1) = 1.

The analytic closed form of the shifted Legendre polynomials of degree i is given by

()

One of the common and efficient methods for solving fractional differential equations of order α > 0is using the series expansion of the form

. For this reason, we define the fractional-order Legendre function by

. Using the properties of the shifted Legendre polynomials and the change of variable z = t^α, it is easy to show that

(1)
,
(2)
, for i⩾1,
(3)
and ,
(4)
and .

In addition,

are orthogonal functions with respect to the weight function w(t) = t^α−1 on (0,1) with

()

The closed form of

is given by

()

Using properties (4) and (5) of the Caputo fractional derivative, one can see that

()

In the next theorem, we state one of the main properties of the fractional Legendre functions which will be used later in this paper.

Theorem 4. For any nonnegative integers p and q,

()

where

()

Proof. For any nonnegative integers p and q,

()

where

()

For the proof of this case, see [25]. Using the change of variables x = 2z − 1 and z = t^α, we obtain the result of the theorem.

Another important result which will facilitate applying the Tau method for fractional case is given in Theorem 5.

Theorem 5. Let u ∈ C[0,1] and u^′(t) be a piecewise continuous function on [0,1]. Then, u(t) can be written in the infinite expansion as , where

()

and w(t) = t^α.

Proof. If u ∈ C¹[−1,1] and u^′′(x) is a piecewise continuous function on [−1,1], converges uniformly to u(x) on [−1,1], see [26–28]. Let h : [0,1] → [−1,1] by

()

Since h(t) is a bijective continuous function,

converges uniformly to u(t) on [0,1]. The value of u_k follows from the orthogonality relation of

with respect to the weight function w(t) = t^α−1 on [0,1]

Theorem 6 gives the relation between the coefficient of the series solution of D^αu(t) and the coefficients of the series expansion of u(t).

Theorem 6. Let u ∈ C¹[0,1] and u^′′(t) be a piecewise continuous function on [0,1]. Then, converges uniformly on [0,1] to D^αu(t), where

()

Proof. Let for n = 0,1, 2, …. From Theorem 5, S_n(t) converges uniformly to u(t) on [0,1]. Since u ∈ C¹[0,1] and u^′′(t) is a piecewise continuous function on [0,1],

()

and (d/dt)S_n(t) converges uniformly to (d/dt)u(t) on [0,1]. Thus,

converges uniformly to

on [0,1] which gives the result of the theorem. The value of a_jk follows from the orthogonality relation of

with respect to the weight function w(t) = t^α−1 on [0,1].

3. Fractional-Order Legendre Tau-Path Following Method

In this section, we present a numerical method for solving problem (1)-(2). We use the fractional-order Legendre Tau method to discretize problem (1)-(2). The result is a nonlinear system. The initial guess that is used in the standard methods for solving the produced nonlinear system is one of the challenges. To overcome this problem, we use the path following method. Approximate the solution y(x), a(x), b(x), c(x), and g(x) in terms of the fractional-order Legendre functions as follows:

()

Thus, D^αy(x) can be approximated by

()

where

is given by Theorem 6. For Y_N, the residual is given by

()

which can be written as

()

where a_j = 0, b_j = 0, y_j = 0, c_j = 0 for j ≥ N + 2, and

for j ≥ N + 1. Using Theorem 4, we can rewrite the residual as

()

Since we are interested in the first n terms only, we ignore higher order terms and we rewrite the residual as

()

Orthogonalize the residual with respect to the fractional-order Legendre function as follows

()

where w(x) = x^α−1. Therefore, (25) leads to the elementwise equation

()

Therefore, we can write (26) as a system of N nonlinear equations in (N + 1) unknowns as

()

where

, and T means the transpose of the matrix.

From the initial condition (2), one can see that

()

where

. From systems (27) and (29), we obtain a system of (N + 1) nonlinear equations in (N + 1) unknowns

()

where Ψ : ℜ^N+1 → ℜ^N+1 by

and

∈ℜ^N+1.

The standard methods for solving system (30), such as secant method and Newton method, need a good initial guess which is not available. To overcome this problem, we look for another method which does not depend on the initial guess. The promise technique is the path following method which is described as follows. From (23), we can see that the function Ω is the sum of three terms. Two of them are linear systems which are

and

. The third term is nonlinear system which is

()

Thus, we can rewrite Ω as

()

where A₁ and A₂ are two N × (N + 1) matrices and Ω₁ : ℜ^N+1 → ℜ^N is a nonlinear function of Y. Hence, system (30) can be written as

()

where

is (N + 1)×(N + 1) matrix and Ψ₁ : ℜ^N+1 → ℜ^N+1 is a nonlinear function of Y given by

. Define the function H : ℜ^N+1 × [0,1] → ℜ^N+1 by

()

Thus, H satisfies the following properties

(1)
H ∈ C^∞(ℜ^N+1 × [0,1]),
(2)
H(0, 0) = 0,
(3)
(∂H/∂Y)(0, 0) = A.

It is worth to mention that A is a nonsingular matrix since AY = R is the system produced by the following problem:

()

which has a unique solution. Hence, it follows from the implicit function theorem that there is a smooth curve γ : I → ℜ^N+1 for some open interval I containing zero such that γ(0) = 0, γ^′(0) ≠ 0, rank⁡(H^′(γ(s))) = N + 1, and

()

for all s ∈ I. Consider the solution γ(s) = (Y(s), λ(s)) (parametrized for convenience with respect to arc length) such that γ(0) = (0, 0). The solution curve H⁻¹(Y(0), λ(0)) should be either diffeomorphic to the circle or to the real line. Since the solution point (0, 0) is unique for λ = 0, it follows that γ cannot be closed, and hence, it is diffeomorphic to the real line. Since γ is a smooth curve, Y(s) is bounded for λ(s) ∈ [0,1]. Moreover, the curve γ reaches the level λ = 1 after a finite arc length s₁. This means,

, and hence,

is the zero of Ψ(Y) − R. Thus, we can take I = [0,1]. For more details about the proof, [29–31]. To apply path following method numerically, we differentiate (36) to get

()

which implies that γ^′(0) is orthogonal to all rows of H^′(γ(0)). Thus, for all s ∈ [0,1],

(1)
,
(2)
∥γ^′(s)∥ = 1, where ∥·∥ is the Euclidean norm,
(3)
H^′(γ(s))γ^′(s) = 0.

We use the predictor-corrector method to numerically trace the curve γ. The predictor step is the Euler-predictor which is given by

()

where Z is a point along the curve γ, and h > 0 is a fixed step size. The corrector step is the Gauss-Newton corrector which is given by

()

where H^′(X) ⁺ = (H^′(X)) ^T(H^′(X)H^′(X) ^T) ⁻¹. For more details, see [31]. Thus, we will start from Z₀ = (0, 0) and then generate the sequence Z₁, Z₂, Z₃, … We stop our procedure at Z_k when the last component of Z_k ≤ 1 and the last component of Z_k+1 > 1. We can write Z_k as Z_k = (Y_k, λ_k). Thus, Y_k will be the approximate solution to the system (33).

4. Numerical Results

In this section, we implement the Tau-Path following method to the nonlinear fractional Riccati differential equations. Two examples of nonlinear fractional Riccati differential equations are solved to show the efficiency of the presented method.

Example 7. Consider the following initial value problem [32]:

()

The matrices in (33) are

()

It is easy to see that |det⁡(A)| = 1 which means A is nonsingular. Define the error by

()

Then, the absolute maximum of the error for different values of α are given in Table 1 for N = 16.

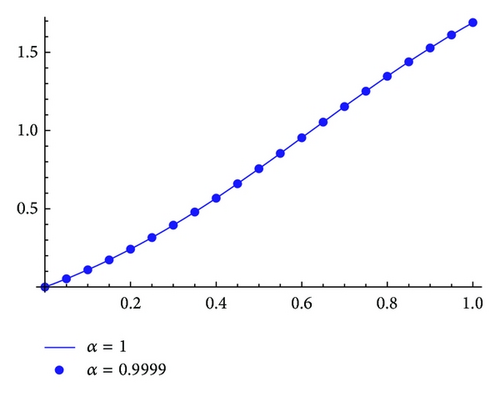
The exact solution when α = 1 is . The graphs of the approximate solution when α = 0.9999 and the graph of the exact solution when α = 1 are given in Figure 1.

α	Error
0.5	1*10⁻⁹
0.9	2*10⁻¹⁰
0.99	1.2*10⁻¹⁰
0.9999	1.7*10⁻¹²

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The graphs of the approximate solution when α = 0.9999 and the graph of the exact solution when α = 1.

Example 8. Consider the following initial value problem [32]:

()

The matrices in (33) are

()

It is easy to see that |det⁡(A)| = 1 which means A is nonsingular. Define the error by

()

Then, the absolute maximum of the error for different values of α is given in Table 2 for N = 16.

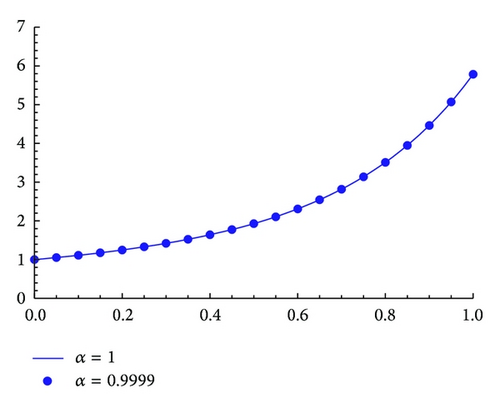
The exact solution when α = 1 is y(x) = (x(J_−3/4(x²/2)Γ(1/4) + J_3/4(x²/2)Γ(3/4)))/(J_1/4(x²/2)Γ(1/4) − 2J_−1/4(x²/2)Γ(3/4)) where J_ν(x) is the Bessel function of first kind. The graphs of the approximate solution when α = 0.9999 and the exact solution when α = 1 are given in Figure 2.

α	Error
0.5	2.7*10⁻¹⁰
0.9	8.6*10⁻¹¹
0.99	5.4*10⁻¹¹
0.9999	2.1*10⁻¹³

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

The authors would like to express their appreciation for the valuable comments of the reviewers. The authors also would like to express their sincere appreciation to United Arab Emirates University for the financial support of Grant no. COS/IRG-15/14.

References

1 Gaul L., Klein P., and Kemple S., Damping description involving fractional operators, Mechanical Systems and Signal Processing. (1991) 5, no. 2, 81–88, 2-s2.0-44949282247.
Google Scholar
2 Podlubny I., Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, 1999, Academic Press, New York, NY, USA.
Google Scholar
3 Al-Khaled K. and Momani S., An approximate solution for a fractional diffusion-wave equation using the decomposition method, Applied Mathematics and Computation. (2005) 165, no. 2, 473–483, 2-s2.0-17644372361, https://doi.org/10.1016/j.amc.2004.06.026.
Google Scholar
4 Das S., Analytical solution of a fractional diffusion equation by variational iteration method, Computers and Mathematics with Applications. (2009) 57, no. 3, 483–487, 2-s2.0-58149263050, https://doi.org/10.1016/j.camwa.2008.09.045.
Google Scholar
5 Suarez L. E. and Shokooh A., An eigenvector expansion method for the solution of motion containing fractional derivatives, Journal of Applied Mechanics, Transactions ASME. (1997) 64, no. 3, 629–634, 2-s2.0-0003001893.
Google Scholar
6 Arikoglu A. and Ozkol I., Solution of fractional integro-differential equations by using fractional differential transform method, Chaos, Solitons and Fractals. (2009) 40, no. 2, 521–529, 2-s2.0-64949197043, https://doi.org/10.1016/j.chaos.2007.08.001.
Google Scholar
7 Meerschaert M. M. and Tadjeran C., Finite difference approximations for two-sided space-fractional partial differential equations, Applied Numerical Mathematics. (2006) 56, no. 1, 80–90, 2-s2.0-28044468843, https://doi.org/10.1016/j.apnum.2005.02.008.
Web of Science® Google Scholar
8 Odibat Z. M. and Shawagfeh N. T., Generalized Taylor′s formula, Applied Mathematics and Computation. (2007) 186, no. 1, 286–293, 2-s2.0-33947277891, https://doi.org/10.1016/j.amc.2006.07.102.
Web of Science® Google Scholar
9 Al-Mdallal Q. M., Syam M. I., and Anwar M. N., A collocation-shooting method for solving fractional boundary value problems, Communications in Nonlinear Science and Numerical Simulation. (2010) 15, no. 12, 3814–3822, 2-s2.0-77952705214, https://doi.org/10.1016/j.cnsns.2010.01.020.
Web of Science® Google Scholar
10 LI Y., Solving a nonlinear fractional differential equation using Chebyshev wavelets, Communications in Nonlinear Science and Numerical Simulation. (2010) 15, no. 9, 2284–2292, 2-s2.0-77949492283, https://doi.org/10.1016/j.cnsns.2009.09.020.
Web of Science® Google Scholar
11 Wu J. L., A wavelet operational method for solving fractional partial differential equations numerically, Applied Mathematics and Computation. (2009) 214, no. 1, 31–40, 2-s2.0-67349274987, https://doi.org/10.1016/j.amc.2009.03.066.
Google Scholar
12 Kilbas A., Srivastave H., and Trujillo J., Theory and Applications of Fractional Differential Equations, North-Hollan Mathematics Studies, 2006, 204, Elsevier Science, Amsterdam, The Netherlands.
Google Scholar
13 Samko S. G., Kilbas A. A., and Marichev O. I., Fractional Integrals and Derivative, 1993, Gordon and Breach, Yverdon, Switzerland, Theory and Applications.
Google Scholar
14 Lakshmikantham V. and Vatsala A., Basic theory of fractional differential equations, Nonlinear Analysis, Theory, Methods & Applications. (2008) 69, no. 8, 2677–2682, https://doi.org/10.1016/j.na.2007.08.042.
Web of Science® Google Scholar
15 Zhang S., Existence of solution for a boundary value problem of fractional order, Acta Mathematica Scientia. (2006) 26, no. 2, 220–228, 2-s2.0-33748915280, https://doi.org/10.1016/S0252-9602(06)60044-1.
10.1016/S0252-9602(06)60044-1
Google Scholar
16 Agarwal R. P., Benchohra M., and Hamani S., A survey on existence results for boundary value problems of nonlinear fractional differential equations and inclusions, Acta Applicandae Mathematicae. (2010) 109, no. 3, 973–1033, 2-s2.0-77949264980, https://doi.org/10.1007/s10440-008-9356-6.
Google Scholar
17 Al-Refai M. and Ali Hajji M., Monotone iterative sequences for nonlinear boundary value problems of fractional order, Nonlinear Analysis, Theory, Methods and Applications. (2011) 74, no. 11, 3531–3539, 2-s2.0-79955561060, https://doi.org/10.1016/j.na.2011.03.006.
Google Scholar
18 Lakshmikantham V. and Vatsala A. S., General uniqueness and monotone iterative technique for fractional differential equations, Applied Mathematics Letters. (2008) 21, no. 8, 828–834, 2-s2.0-45049084850, https://doi.org/10.1016/j.aml.2007.09.006.
Google Scholar
19 Pao C. V., Nonlinear Parabolic and Elliptic Equations, 1992, Plenum Press, New York, NY, USA.
Google Scholar
20 Oldham K. and Spanier J., The Fractional Calculus, 1974, Academic, New York, NY, USA.
Google Scholar
21 Esmaeili S., Shamsi M., and Luchko Y., Numerical solution of fractional differential equations with a collocation method based on Mntz polynomials, Computers and Mathematics with Applications. (2011) 62, no. 3, 918–929, 2-s2.0-79961002199, https://doi.org/10.1016/j.camwa.2011.04.023.
Google Scholar
22 Khan N. A., Ara A., and Jamil M., An efficient approach for solving the Riccati equation with fractional orders, Computers and Mathematics with Applications. (2011) 61, no. 9, 2683–2689, 2-s2.0-79955474354, https://doi.org/10.1016/j.camwa.2011.03.017.
Google Scholar
23 Cang J., Tan Y., Xu H., and Liao S.-J., Series solutions of non-linear Riccati differential equations with fractional order, Chaos, Solitons and Fractals. (2009) 40, no. 1, 1–9, 2-s2.0-64549148828, https://doi.org/10.1016/j.chaos.2007.04.018.
Google Scholar
24 Caputo M., Linear models of dissipation whose Q is almost frequency independent, Part II Geophys, Mathematics & Physical Sciences. (1967) 13, no. 5, 529–539, https://doi.org/10.1111/j.1365-246X.1967.tb02303.x.
Google Scholar
25 Al-Salam W. A., On the product of two Legendre polynomials, Mathematica Scandinavica. (1956) 4, 239–242.
Google Scholar
26 Siyyam H. I. and Syam M. I., An accurate solution of the Poisson equation by the Chebyshev-Tau method, Journal of Computational and Applied Mathematics. (1997) 85, no. 1, 1–10, 2-s2.0-0031556715.
Google Scholar
27 Canuto C., Hussaini M. Y., Quarteroni A., and Zang T. A., Spectral Methods in Fluid Dynamics, 1988, Springer, New York, NY, USA.
Google Scholar
28 Canuto C., Hussaini M. Y., Quarteroni A., and Zang T. A., Spectral Methods: Fundamentals in Single Domains, 2006, Springer, New York, NY, USA.
Google Scholar
29 Allgower E. L. and Georg K., Numerical Continuation Methods, 1990, Springer, New York, NY, USA.
Google Scholar
30 Syam M. I. and Al-Sharo′ S. M., Collocation-continuation technique for solving nonlinear ordinary boundary value problems, Computers and Mathematics with Applications. (1999) 37, no. 10, 11–17, 2-s2.0-0033132975, https://doi.org/10.1016/S0898-1221(99)00121-2.
Google Scholar
31 Siyyam H. I. and Syam M. I., The modified trapezoidal rule for line integrals, Journal of Computational and Applied Mathematics. (1997) 84, no. 1, 1–14, 2-s2.0-0031249233.
Google Scholar
32 Merdan M., On the solutions fractional Riccati di¤erential equation with modifed Riemann-Liouville derivative, International Journal of Differential Equations. (2012) 2012, 1–17.
Google Scholar

Citing Literature

All articles

Tau-Path Following Method for Solving the Riccati Equation with Fractional Order

Abstract

1. Introduction

2. Preliminaries

3. Fractional-Order Legendre Tau-Path Following Method

4. Numerical Results

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Tau-Path Following Method for Solving the Riccati Equation with Fractional Order

Abstract

1. Introduction

2. Preliminaries

3. Fractional-Order Legendre Tau-Path Following Method

4. Numerical Results

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Related

Information