The finite-time stability and stabilization problems of a class of networked control systems (NCSs) with bounded Markovian packet dropout are investigated. The main results provided in the paper are sufficient conditions for finite-time stability and stabilization via state feedback. An iterative approach is proposed to model NCSs with bounded packet dropout as jump linear systems (JLSs). Based on Lyapunov stability theory and JLSs theory, the sufficient conditions for finite-time stability and stabilization of the underlying systems are derived via linear matrix inequalities (LMIs) formulation. Lastly, an illustrative example is given to demonstrate the effectiveness of the proposed results.

1. Introduction

The concept of Lyapunov asymptotic stability is largely known to the control community; see [1] and the references therein. However, often Lyapunov asymptotic stability is not enough for practical applications, because there are some cases where large values of state variables are not acceptable. For this purpose, the concept of finite-time stability (FTS) can be used. Some early results on FTS can be found in [2]; more recently the concept of FTS has been revisited in the light of recent results coming from linear matrix inequalities (LMIs) theory, which has made it possible to find less conservative conditions for guaranteeing FTS and finite time stabilization of discrete-time and continuous-time systems [3, 4]. In [5], finite-time stabilization of linear time-varying systems has been studied. In [6–8], finite-time control problem for the impulsive systems is discussed. In [9], sufficient conditions for finite-time stability and stabilization of a class of nonlinear quadratic systems are also presented. For more analysis and synthesis results of finite control problem, the readers are referred to the literature [10, 11] and the references therein. In [12], sufficient conditions for finite-time boundness and stability of switched system are proposed, and static state and dynamic output feedback controllers are designed to finite-time stabilise switched linear systems. In [13], a new design approach is proposed for robust finite-time H_∞ control of a class of Markov jump systems with partially known information. In [14], finite-time reliable guaranteed cost fuzzy control for discrete-time nonlinear systems with actuator faults is investigated. In [15], the finite-time stochastic synchronization problem for complex networks with stochastic noise perturbations is studied. In [16], finite-time synchronization of the singular hybrid coupled networks is investigated.

On the other hand, NCSs are feedback control systems with control loops closed via digital communication channels. Compared with the traditional point-to-point wiring, the use of the communication channels can reduce the costs of cables and power, simplify the installation and maintenance of the whole system, and increase the reliability. Because of these attractive benefits, many industrial companies and institutes have shown interest in applying networks for remote industrial control purposes and factory automation [17]. However, the insertion of communication networks in feedback control loops makes the NCSs analysis and synthesis complex; see [18–20] and the references therein, where much attention has been paid to the delayed data packets of an NCSs due to network transmissions. In fact, data packets through networks suffer not only transmission delays, but also, possibly, packet dropout [21, 22]; the latter is a potential source of instability and poor performance in NCSs because of the critical real-time requirement in control systems.

So far, Lyapunov stability analysis for NCSs with packet dropout has been extensively studied by many researchers [23–25]. However, to date and to the best of our knowledge, the problems of finite-time stabilization of NCSs with Markovian packet dropout have not been fully investigated and still remain challenging, although results related to systems over networks with packet loss are reported in the existing literature, which motivates the study of this paper. The main contributions are given as follows: (1) definitions of finite-time stabilization are extended to NCSs with packet dropout; (2) sufficient conditions for finite-time stabilization in terms of linear matrix inequalities formulation are given.

This paper is organized as follows. An iterative method to model NCSs with bounded Markovian packet dropout as MJLSs is proposed in Section 2. The stochastic stability and stabilization conditions for NCSs are derived via LMIs in Section 3. Section 4 provides numerical examples to illustrate the effectiveness of our results. Finally, Section 5 gives some concluding remarks.

Notations. Throughout this paper, for two matrices A and B, A < B means that A − B is negative definite, and A^T denotes the transpose of A. E{·} stands for the mathematical expectation operator. λ_max⁡(A) and λ_min⁡(A) denote the maximum and minimum eigenvalue of A, respectively. I is the identity matrix.

2. Problem Formulation and Preliminaries

The framework of NCSs considered in this paper is depicted in Figure 1, and the plant to be controlled is described by the following linear discrete-time systems:

()

where x(k) ∈ ℝⁿ is the state and u(k) ∈ ℝ^m is the control input. A and B are known real constant matrices with appropriate dimensions. We assume that (A, B) is controllable.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Illustration of NCSs over communication network.

Let ℐ = {i₁, i₂, …}, which is a subsequence of ℕ = {1,2, …}, denote the sequence of time points of successful date transmission from sensor to actuator. The state feedback controller law is

()

where K ∈ ℝ^m×n is to be designed. The control input is held at the previous value by the zero-order hold during the two successively successful transmitted instant; that is

()

Thus the closed-loop system is

()

Applying iteratively (4), we can obtain

()

Define the packet dropout process as follows:

()

which takes values in the finite state space 𝒮 = {1,2, …, s}, where s is defined as

()

Then the closed-loop system (5) can be rewritten as jump linear systems:

()

The packet dropout process {r(i_k)} is described by a discrete-time homogeneous Markov chain with mode transition probabilities:

()

The corresponding transition probabilities is defined as

()

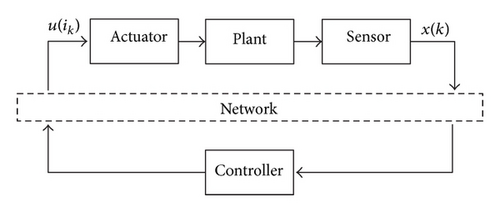
Remark 1. It is worth pointing out that the packet dropout process {r(i_k), i_k ≥ 0} includes both sensor-to-controller and controller-to-actuator packet dropouts.

The main aim of this paper is to find some sufficient conditions which guarantee that the system given (8) is stable over a finite-time interval. This concept can be formalized through the following definition.

Definition 2. System (8) is said to be finite-time stable with respect to (α, β, R, N), where R is a positive-definite matrix, 0 < α < β, if

()

To this end, the following lemmas will be essential for the proofs in the next section and theirs proofs can be found in the cited reference.

Lemma 3 (see [26].)For any matrices U ∈ R^n×n and V ∈ R^n×n, if the matrix V > 0, then one has

()

Lemma 4 (Schur complement lemma; see [26]). For a given symmetric matrix

()

where W₁₁ ∈ ℝ^p×p, W₂₂ ∈ ℝ^q×q, and W₁₂ ∈ ℝ^p×q, then the following three conditions are mutually equivalent:

(1)
W < 0,
(2)
W₁₁ < 0, ,
(3)
W₂₂ < 0, .

3. Main Results

In this section, we will find a state feedback control matrix K, such that system (8) is finite-time stable with respect to (α, β, R, N). In order to solve the problem, the following theorem will be essential.

Theorem 5. For a constant γ > 0, system (8) is finite-time stable with respect to (α, β, R, N) if there exist matrix P_i > 0, i ∈ 𝒮, and two scalars λ₁, λ₂, such that the following conditions hold:

()

where

()

Proof. Choose the Lyapunov function as

()

Firstly, we will prove that conditions (14) combined with the following condition

()

imply that (8) is finite-time stable with respect to (α, β, R, N), where ζ is difference operator and defined as follows:

()

Applying iteratively (18), we obtain

()

Note that

()

Thus, we have

()

From conditions (14), we can obtain

()

Secondly, we will prove that condition (15) is equivalent to condition (18). According to the definition of difference operator ζ and the transition probabilities of the packet dropout process {r(i_k)}, we can obtain

()

which yields that

()

Now we turn back to our original problem, which is to find sufficient conditions which guarantee that the system (8) with the controller (2) is finite-time stable with respect to (α, β, R, N). The solution of this problem is given by the following theorem.

Theorem 6. For a constant γ > 0, system (8) is finite-time stable with respect to (α, β, R, N) if there exist matrix , i ∈ 𝒮, G ∈ ℝ^n×n, Y ∈ ℝ^m×n, and two scalars λ₁, λ₂, such that the following conditions hold:

()

where

()

Then the desired stabilizable control matrix is given by

()

Proof. By Lemma 4, (27) is equivalent to

()

From Lemma 3, we can obtain

()

Denote

. From (30) and (31), we have

()

Let Y = KG. Then, we can obtain

()

which yields that

()

which is equivalent to

()

In view of Theorem 5, system (8) is finite-time stable with respect to (α, β, R, N). Moreover, the desired controller gain is given by (29).

Remark 7. For the case of i_k < l ≤ i_k+1 − 1, the system transient performance can also be accommodated. In fact, denote h(i_k) = l − i_k ∈ 𝒮. Then we have

()

By Theorem 6, the system transient performance can be accommodated.

4. Numerical Example

In this section, a numerical example is given to illustrate the effectiveness of the proposed methods. Let us consider the continuous time system [27]:

()

where

()

When the plant is sampled with a sampling period T = 0.5s, the corresponding discretized system is

()

Both the continuous time system and discretized system are unstable because the eigenvalues of

are −0.5, −1, 0.5 and the eigenvalues of A are 0.7788, 0.6065, 1.2840. Furthermore, we assume that the packet dropout upper bound is s = 4 and the transition probabilities matrix is as follows:

()

For given γ = 1, α = 1, β = 10, R = I, N = 5, according to Theorem 6, the control matrix is given by

()

To simulate, we take the initial state as x₀ = [−5 0 5] ^T. Figure 2 depicts the trajectory of the system state. The numerical example and simulation demonstrate the effectiveness of the proposed results.

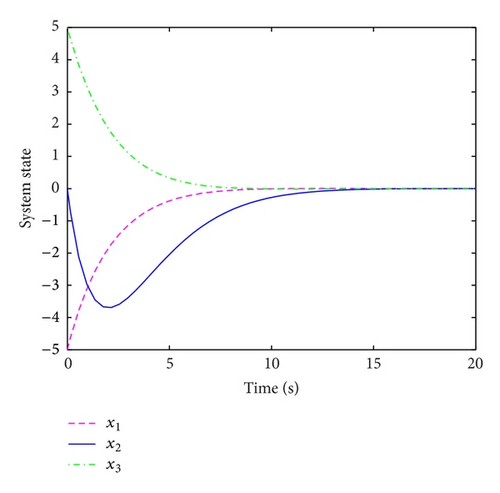
5. Conclusions

In this paper, we have considered the finite-time stabilization problems of a class of networked control systems (NCSs) with bounded Markovian packet dropout, based on the iterative approach the NCSs with bounded packet dropout as jump linear systems. The sufficient conditions for finite-time stabilization of the underlying systems are derived via linear matrix inequalities (LMIs) formulation. Lastly, an illustrative example is given to demonstrate the effectiveness of the proposed results.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

This work was partly supported by the University Natural Science Foundation of Anhui Province no. KJ2013A239 and the University Special Foundation for Young Scientists of Anhui Province no. 2013SQRW052ZD.

References

1 Cao J., Alofi A., Al-Mazrooei A., and Elaiw A., Synchronization of switched interval networks and applications to chaotic neural networks, Abstract and Applied Analysis. (2013) 2013, 11, https://doi.org/10.1155/2013/940573, 940573, MR3143573.
10.1155/2013/940573
Google Scholar
2 Weiss L. and Infante E. F., Finite time stability under perturbing forces and on product spaces, IEEE Transactions on Automatic Control. (1967) 12, 54–59, MR0209589, ZBL0168.33903.
10.1109/TAC.1967.1098483
Web of Science® Google Scholar
3 Amato F. and Ariola M., Finite-time control of discrete-time linear systems, IEEE Transactions on Automatic Control. (2005) 50, no. 5, 724–729, https://doi.org/10.1109/TAC.2005.847042, MR2141582.
10.1109/TAC.2005.847042
Web of Science® Google Scholar
4 Amato F., Ariola M., and Cosentino C., Finite-time stabilization via dynamic output feedback, Automatica. (2006) 42, no. 2, 337–342, https://doi.org/10.1016/j.automatica.2005.09.007, MR2195173, ZBL1099.93042.
10.1016/j.automatica.2005.09.007
Web of Science® Google Scholar
5 Garcia G., Tarbouriech S., and Bernussou J., Finite-time stabilization of linear time-varying continuous systems, IEEE Transactions on Automatic Control. (2009) 54, no. 2, 364–369, https://doi.org/10.1109/TAC.2008.2008325, MR2491966.
10.1109/TAC.2008.2008325
Web of Science® Google Scholar
6 Liu L. and Sun J., Finite-time stabilization of linear systems via impulsive control, International Journal of Control. (2008) 81, no. 6, 905–909, https://doi.org/10.1080/00207170701519060, MR2419413, ZBL1149.93338.
10.1080/00207170701519060
Web of Science® Google Scholar
7 Zhao S., Sun J., and Liu L., Finite-time stability of linear time-varying singular systems with impulsive effects, International Journal of Control. (2008) 81, no. 11, 1824–1829, https://doi.org/10.1080/00207170801898893, MR2462577, ZBL1148.93345.
10.1080/00207170801898893
Web of Science® Google Scholar
8 Amato F., Ambrosino R., Ariola M., and Cosentino C., Finite-time stability of linear time-varying systems with jumps, Automatica. (2009) 45, no. 5, 1354–1358, https://doi.org/10.1016/j.automatica.2008.12.016, MR2531617, ZBL1162.93375.
10.1016/j.automatica.2008.12.016
Web of Science® Google Scholar
9 Amato F., Cosentino C., and Merola A., Sufficient conditions for finite-time stability and stabilization of nonlinear quadratic systems, IEEE Transactions on Automatic Control. (2010) 55, no. 2, 430–434, https://doi.org/10.1109/TAC.2009.2036312, MR2604419.
10.1109/TAC.2009.2036312
Web of Science® Google Scholar
10 Amato F., Ariola M., and Cosentino C., Finite-time stability of linear time-varying systems: analysis and controller design, IEEE Transactions on Automatic Control. (2010) 55, no. 4, 1003–1008, https://doi.org/10.1109/TAC.2010.2041680, MR2654445.
10.1109/TAC.2010.2041680
Web of Science® Google Scholar
11 Amato F., Ariola M., and Cosentino C., Finite-time control of discrete-time linear systems: analysis and design conditions, Automatica. (2010) 46, no. 5, 919–924, https://doi.org/10.1016/j.automatica.2010.02.008, MR2877166, ZBL1191.93099.
10.1016/j.automatica.2010.02.008
Web of Science® Google Scholar
12 Xiang W. and Xiao J., Finite-time stability and stabilisation for switched linear systems, International Journal of Systems Science. (2013) 44, no. 2, 384–400, https://doi.org/10.1080/00207721.2011.604738, MR3000754.
10.1080/00207721.2011.604738
Web of Science® Google Scholar
13 Luan X., Liu F., and Shi P., Robust finite-time control for a class of extended stochastic switching systems, International Journal of Systems Science. (2011) 42, no. 7, 1197–1205, https://doi.org/10.1080/00207720903428898, MR2817854, ZBL1230.93098.
10.1080/00207720903428898
Web of Science® Google Scholar
14 Yang D. and Cai K.-Y., Finite-time reliable guaranteed cost fuzzy control for discrete-time nonlinear systems, International Journal of Systems Science. (2011) 42, no. 1, 121–128, https://doi.org/10.1080/00207720903470163, MR2736514, ZBL1209.93088.
10.1080/00207720903470163
Web of Science® Google Scholar
15 Yang X. and Cao J., Finite-time stochastic synchronization of complex networks, Applied Mathematical Modelling. (2010) 34, no. 11, 3631–3641, https://doi.org/10.1016/j.apm.2010.03.012, MR2651795, ZBL1201.37118.
10.1016/j.apm.2010.03.012
Web of Science® Google Scholar
16 Zheng C. and Cao J., Finite-time synchronization of singular hybrid coupled networks, Journal of Applied Mathematics. (2013) 2013, 8, https://doi.org/10.1155/2013/378376, 378376, MR3045405, ZBL1266.90055.
10.1155/2013/378376
Google Scholar
17 Walsh G. C. and Ye H., Scheduling of networked control systems, IEEE Control Systems Magazine. (2001) 21, no. 1, 57–65.
10.1109/37.898792
Web of Science® Google Scholar
18 Tahoun A. H. and Fang H.-J., Adaptive stabilisation of networked control systems tolerant to unknown actuator failures, International Journal of Systems Science. (2011) 42, no. 7, 1155–1164, https://doi.org/10.1080/00207720903308975, MR2817850, ZBL1230.93073.
10.1080/00207720903308975
Web of Science® Google Scholar
19 Liu M. and You J., Observer-based controller design for networked control systems with sensor quantisation and random communication delay, International Journal of Systems Science. (2012) 43, no. 10, 1901–1912, https://doi.org/10.1080/00207721.2011.555013, MR2965020.
10.1080/00207721.2011.555013
CAS Web of Science® Google Scholar
20 Wang P., Han C. Z., and Ding B. C., Stability of discrete-time networked control systems and its extension for robust H_∞ control, International Journal of Systems Science. (2013) 44, no. 2, 275–288, https://doi.org/10.1080/00207721.2011.600474, MR3000746.
10.1080/00207721.2011.600474
CAS Web of Science® Google Scholar
21 Yue D., Han Q. L., and Peng C., State feedback controller design of networked control systems, IEEE Transactions on Circuits and Systems II: Express Briefs. (2004) 51, no. 11, 640–644.
10.1109/TCSII.2004.836043
Web of Science® Google Scholar
22 Zhang L., Shi Y., Chen T., and Huang B., A new method for stabilization of networked control systems with random delays, IEEE Transactions on Automatic Control. (2005) 50, no. 8, 1177–1181, https://doi.org/10.1109/TAC.2005.852550, MR2156045.
10.1109/TAC.2005.852550
Web of Science® Google Scholar
23 Yu J. Y., Wang L., and Yu M., Stabilization of networked control systems via packet-loss dependent output feedback controllers, Proceedings of the American Control Conference, 2008, 3620–3625.
Google Scholar
24 Zhang D. and Wang X., Static output feedback control of networked control systems with packet dropout, International Journal of Systems Science. (2012) 43, no. 4, 665–672, https://doi.org/10.1080/00207721.2010.517873, MR2889681.
10.1080/00207721.2010.517873
Web of Science® Google Scholar
25 Zhang X. M., Zheng Y. F., and Lu G. P., Stochastic stability of networked control systems with network-induced delay and data dropout, Journal of Control Theory and Applications. (2008) 6, no. 4, 405–409, https://doi.org/10.1007/s11768-008-6160-9, MR2474304.
10.1007/s11768-008-6160-9
Google Scholar
26 Sun Y. and Qin S., Stability analysis and controller design for networked control systems with random time delay, International Journal of Systems Science. (2011) 42, no. 3, 359–367, https://doi.org/10.1080/00207720903513368, MR2747611, ZBL1209.93159.
10.1080/00207720903513368
Web of Science® Google Scholar
27 Yue D., Han Q.-L., and Lam J., Network-based robust H_∞ control of systems with uncertainty, Automatica. (2005) 41, no. 6, 999–1007, https://doi.org/10.1016/j.automatica.2004.12.011, MR2157699, ZBL1091.93007.
10.1016/j.automatica.2004.12.011
Web of Science® Google Scholar

Citing Literature

All articles

Finite-Time Stability and Stabilization of Networked Control Systems with Bounded Markovian Packet Dropout

Abstract

1. Introduction

2. Problem Formulation and Preliminaries

3. Main Results

4. Numerical Example

5. Conclusions

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Finite-Time Stability and Stabilization of Networked Control Systems with Bounded Markovian Packet Dropout

Abstract

1. Introduction

2. Problem Formulation and Preliminaries

3. Main Results

4. Numerical Example

5. Conclusions

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Related

Information