Journal of Computational Methods in Physics
Volume 2013, Issue 1 939143
Research Article
Open Access

A New Spectral-Homotopy Perturbation Method and Its Application to Jeffery-Hamel Nanofluid Flow with High Magnetic Field

Ahmed A. Khidir, 

Corresponding Author

Ahmed A. Khidir

Faculty of Technology of Mathematical Sciences and Statistics, Alneelain University, Algamhoria Street, P.O. Box 12702, Khartoum, Sudan neelain.edu.sd

Search for more papers by this author
First published: 30 December 2013
https://doi.org/10.1155/2013/939143
Academic Editor: Ali Cemal Benim

Abstract

We present a new modification of the homotopy perturbation method (HPM) for solving nonlinear boundary value problems. The technique is based on the standard homotopy perturbation method, and blending of the Chebyshev pseudospectral methods. The implementation of the new approach is demonstrated by solving the Jeffery-Hamel flow considering the effects of magnetic field and nanoparticle. Comparisons are made between the proposed technique, the standard homotopy perturbation method, and the numerical solutions to demonstrate the applicability, validity, and high accuracy of the present approach. The results demonstrate that the new modification is more efficient and converges faster than the standard homotopy perturbation method.

1. Introduction

Many problems in the fields of physics, engineering, and biology are modeled by coupled linear or nonlinear systems of partial or ordinary differential equations. Compared to nonlinear equations, linear equations can be easily solved and finding analytical solutions to nonlinear problems on finite or infinite domains is one of the most challenging problems. Such problems do not usually admit closed from analytic solutions and in most cases we look for finding approximate solutions using numerical approximation techniques. Nonnumerical approaches include the classical power-series method and its variants for systems of nonlinear differential equations with small or large embedded parameters. One of these methods is the homotopy perturbation method (HPM). This method, which is a combination of homotopy in topology and classic perturbation techniques, provides us with a convenient way to obtain analytic or approximate solutions for a wide variety of problems arising in different scientific fields by continuously deforming the difficult problem into a set of simple linear problems that are easy to solve. It was proposed first by He [1–4]. He has successfully used the method to solve many types of linear and nonlinear differential equations such as Lighthill equation [1], Duffing equation [2], Blasius equation [5], wave equations [4], and boundary value problems [6]. Homotopy perturbation method has been recently intensively studied by many authors and they used the method for solving nonlinear problems and some modifications of this method have been published [7–12] to facilitate, make accurate calculations, and accelerate the rapid convergence of the series solution and reduce the size of work. Jalaal et al. [13] used HPM to investigate the acceleration motion of a vertically falling spherical particle in incompressible Newtonian media. Jalaal and Ganji [14] applied HPM successfully on the problem of unsteady rolling motion of spheres in inclined tubes filled with incompressible Newtonian fluids. They found that the inclination angle does not affect the acceleration duration.

The application of the homotopy perturbation method in linear and non-linear models has been developed by many scientists and engineers, because this method provides us with a convenient way to obtain analytic or approximate solutions for a wide variety of problems arising in different scientific fields by continuously deforming the difficult problem into a set of simple linear problems that are easy to solve (e.g., see [12, 15, 16]).

The homotopy perturbation method has been applied on the MHD Jeffery-Hamel problem by [17]. This model is one of the most applicable cases of the incompressible viscous fluid flow through convergent-divergent channels in fluid mechanics, civil, environmental, mechanical, and bio-mechanical engineering. Jeffery [18] and Hamel [19] were the first persons who discussed this case, and so it is known as Jeffery-Hamel problem. They presented an exact similarity solution of the Navier-Stokes equations in the special case of two-dimensional flow through a channel with inclined plane walls meeting at a vertex and with a source or sink at the vertex. The problem has been well extensively studied by several authors and discussed in many articles and textbooks. The study of [20] considers the steady two-dimensional radial flow of viscous fluid between plane walls which either converge or diverge. In the Ph.D. thesis [21], we find that Jeffery-Hamel flow is used as asymptotic boundary conditions to examine steady two-dimensional flow of a viscous fluid in a channel. But, here, certain symmetric solutions of the flow have been considered, although asymmetric solutions are both possible and of physical interest [22]. The classical Jeffery-Hamel problem was extended in [23] to include the effects of an external magnetic field on an electrically conducting fluid. Recent studies to solving the Jeffery-Hamel flow problem include perturbation techniques [24], Adomian decomposition method [25–27], homotopy analysis method [28–30], optimal homotopy asymptotic method [31], and variational iteration method [17].

In this work, we present an alternative and improved form of the HPM called spectral-homotopy perturbation method (SHPM) that blends the traditional homotopy perturbation method with the Chebyshev spectral collocation method. The advantage of this approach is that it is more flexible than HPM for choosing a linear operator and initial guess. In HPM, one is restricted to choosing a linear operator and initial approximation that would make the integration of the higher-order differential equations possible whereas the SHPM allows us to have a wider range of selecting linear operators and an initial guess may be used as long as it satisfies the boundary conditions.

We have applied the new technique to find an approximate solution of MHD Jeffery-Hamel flow and to study the effect of nanoparticle volume fraction on the velocity profile. We have made a comparison between the current results and the numerical solutions in plots and tables to show the applicability, validity, and accuracy of this method. The obtained results give rapid convergence, good accuracy and suggest that this newly improvement technique introduces power for solving nonlinear boundary value problems and several advantages of the SHPM over the HPM approach are also pointed out.

2. Mathematical Formulation

We consider the steady two-dimensional flow of an incompressible conducting viscous fluid from a source or sink at the intersection between two rigid plane walls that the angel between them is 2α as shown in Figure 1. The grid walls are considered to be divergent if α > 0 and convergent if α < 0. We assume that the velocity is only along radial direction and depends on r and θ so that v = (u(r, θ), 0) only and, further, we assume that there is no magnetic field in the z-direction. The velocity is assumed only along radial direction and depends on r and θ. Conservation of mass and momentum for two-dimensional flow in the cylindrical coordinate can be expressed as follows:
()
()
()
where P is the fluid pressure, B0 is the electromagnetic induction, and σ is the conductivity of the fluid.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Geometry of the MHD Jeffery-Hamel flow.
The effective density ρnf, the effective dynamic viscosity μnf, and the kinematic viscosity υnf of the nanofluid are given as [33, 34]
()
Here, ϕ is the solid volume fraction, μf is the viscosity of the basic fluid, and ρf and ρs are the densities of the pure fluid and nanoparticle, respectively. The continuity equation (1) implies that
()
Using the following dimensionless parameters [28]:
()
and eliminating P from (2) and (3), we obtain the following third-order non-linear ordinary differential equation for the normalized function profile F(η):
()
subject to the boundary conditions
()
where Re is the Reynolds number given by
()
where Umax  is the velocity at the center of the channel (r = 0) and is the Hartmann number.

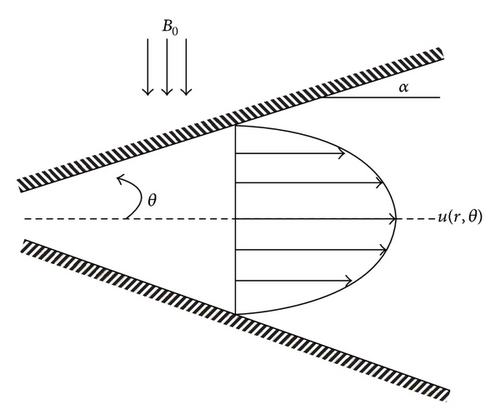
3. Homotopy Perturbation Method

To illustrate the basic ideas of the homotopy perturbation method, we consider the following nonlinear differential equation:
()
with the boundary conditions
()
where A is a general operator, B is a boundary operator, f(r) is a known analytic function, and Γ is the boundary of the domain Ω. The operator A can, generally speaking, be divided into two parts, L and N, where L is linear and N is nonlinear. Equation (10) can therefore be written as follows:
()
By the homotopy technique [29, 30], we construct a homotopy v(r, p) : Ω × [0,1] → ℜ which satisfies
()
or
()
where p ∈ [0,1] is an embedding parameter and u0 is an initial approximation of (10), which satisfies the boundary conditions. Obviously, from (13), we have
()
We can assume that the solution of (10) can be written as a power series in p, as follows:
()
Setting p = 1 results in the approximation to the solution of (10)
()

4. Spectral-Homotopy Perturbation Method

The basic idea of SHPM for solving a non-linear differential equation is summarized as follows:
  • (1)

    linearize the non-linear differential equation by applying HPM,

  • (2)

    rewrite the resulting linear differential equation in a system of linear equations using Chebyshev pseudospectral collocation method,

  • (3)

    solve the system of equations to get the solution of origin differential equation.

In this section, we describe the new technique of SHPM for solving the governing MHD Jeffery-Hamel problem. The method is based on Chebyshev pseudospectral collocation methods and on the HPM described in the previous section. In applying the SHPM, we begin by transforming the physical region [0,1] into the region [−1,1] on which the Chebyshev spectral method can be applied by using the transformations
()
It is also convenient to make the boundary conditions homogeneous by using the transformation
()
Substituting (18) and (19) in the governing equation (7) gives
()
Equation (20) is solved subject to the boundary conditions
()
where
()
The initial approximation for the solution of (20) is taken to be the solution of the nonhomogeneous linear part of (20) which is given by
()
subject to the boundary conditions
()
The solution of (23) and (24) can be obtained by applying the Chebyshev pseudospectral method (see [35, 36] for details). The unknown function f0(ξ) is approximated as a truncated series of Chebyshev polynomials of the form
()
where Tk is the kth Chebyshev polynomial, fk are coefficients, and ξ0, ξ1, …, ξN are Gauss-Lobatto collocation points defined by [35]
()
The derivatives of the function f0(ξ) at the collocation points are represented as
()
where r is the order of differentiation and D = 2𝒟 with 𝒟 being the Chebyshev spectral differentiation matrix whose entries are defined as (see, e.g., [35])
()
Substituting (25)–(27) in (23) and (24) yields
()
subject to the boundary conditions
()
where
()
where diag [] is a diagonal matrix of size N × N and T denotes the transpose. The matrix A has dimensions N × N while matrix Φ has dimensions N × 1. To incorporate the boundary conditions (24) to (29), we delete the first and the last rows and columns of A and delete the first and last elements of f0 and Φ. The condition is incorporated on the resulting of the modified matrix A by replacing last row with the last row of Chebyshev spectral differentiation matrix and setting the resulting last element of the modified matrix Φ to be zero as shown in the following equation:
()
Thus, the solution f0 is determined from the equation
()
where and are the modified matrices of A and Φ, respectively. The solution (33) provides us with the initial approximation for the SHPM solution of (20). The higher approximations are obtained by constructing a homotopy for the government equation (20) as follows:
()
where ℒ is a linear operator which is taken to be
()
and F is an approximate series solution of (20) given by
()
Substituting (35) and (36) in (34) gives
()
To get more higher-order approximations for (20), we compare between the coefficients of pi of both sides in (37). We have
()
where χ = 0 if i = 1 and χ = 1 if i > 1. Thus, the ith-order approximation is given by the following system of matrices:
()
subject to the boundary conditions
()
()
where fi = [fi(ξ0), fi(ξ1), …, fi(ξN)] T and a3 = diag [a3(η0), a3(η1), …, a3(ηN)] T. To incorporate the boundary conditions (40) to (39), we delete the first and the last rows and columns of A and delete the first and last elements of fi and Bi. The boundary condition is incorporated on the resulting of the modified matrix A by replacing last row by the last row of Chebyshev spectral differentiation matrix and setting the resulting last element of the modified matrix Bi to be zero. Finally, the solution fi is determined from the following equation:
()
where is the modified matrix of Bi. Thus, starting from the initial approximation f0, higher-order approximations fm, for m ≥ 1, can be obtained through the recursive formula (42). The solution (42) provides us with the highest order approximation for the SHPM solution of the governing equation (20). The series fi is convergent for most cases. However, the convergence rate depends on the nonlinear operator of (20). The following opinions are suggested and proved by He [1, 2]:
  • (i)

    the second derivative of N(v) with respect to v must be small because the parameter p may be relatively large; that is, p → 1;

  • (ii)

    the norm of L−1(∂N/∂v) must be smaller than one so that the series converges.

This is the same strategy that is used in the SHPM approach.

Here, we observe that the main difference between HPM and SHPM is that the solutions are obtained by solving a system of higher-order ordinary differential equations in the HPM while for the SHPM solutions are obtained by solving a system of linear algebraic equations of the form (42) that are easier to solve.

5. Results and Discussion

In this section, we present the results obtained using the SHPM and the numerical solution for MHD Jeffery-Hame, flow with nanoparticle. Here, we used the inbuilt MATLAB boundary value problem solver bvp4c for the numerical solution approach. In generating the presented results, it was determined through numerical experimentation that N = 80 and we considered the fourth-order of SHPM which gave sufficient accuracy for the method. In this study, copper (Cu) is considered as nanoparticles with water being as the base fluid and we assumed that the base fluid and the nanoparticles are in thermal equilibrium and no slip occurs between them. The density of water is ρf = 997.1 and the density of Cu is ρs = 8933.

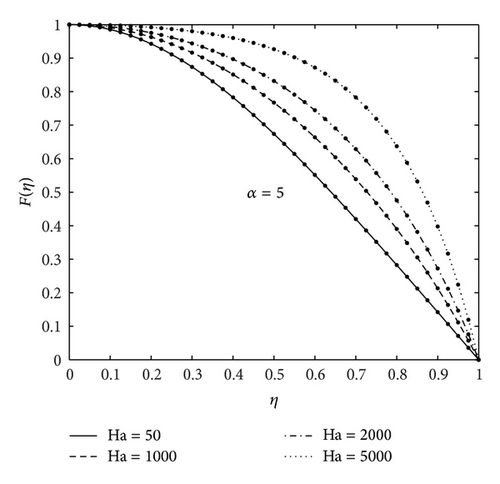
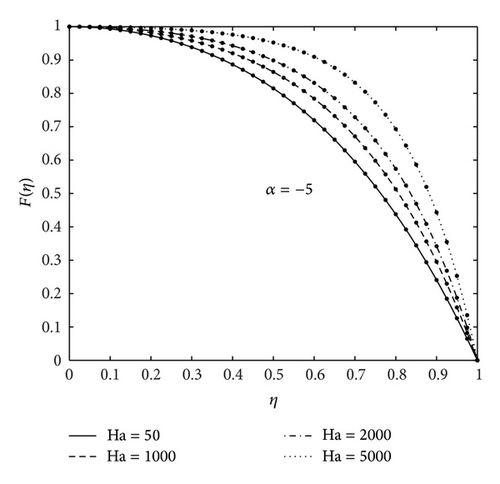
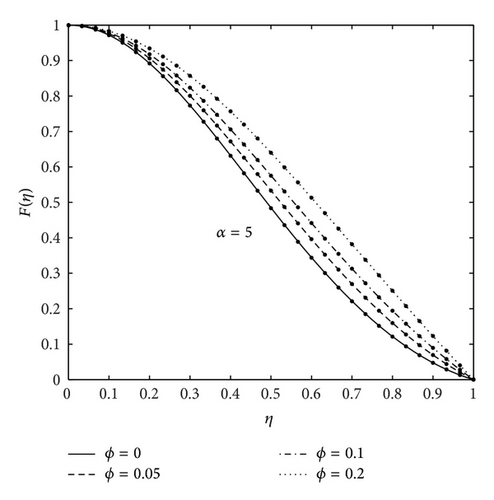
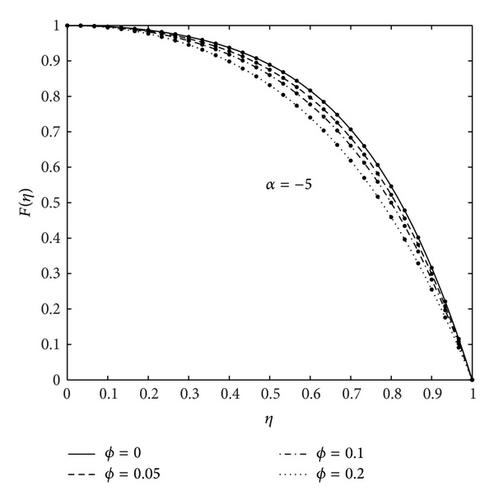
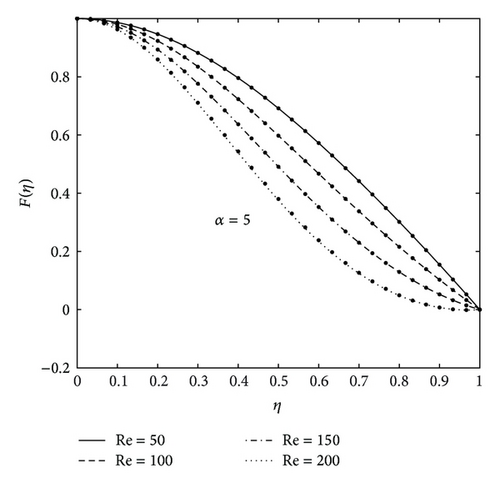
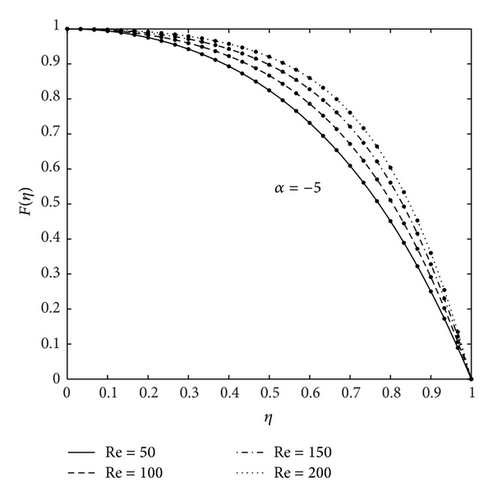
Figures 2 and 3 show, firstly, the influence of the various physical parameters on the velocity profiles and, secondly, a comparison between the present results and numerical results to give a sense of the accuracy and convergence rate of the SHPM. The figures show that there is very good match between the two sets of results even at very low orders of SHPM approximations series compared with the numerical results. These findings firmly establish SHPM as an accurate alternative to HPM. Table 1 gives a comparison of SHPM results at 2nd and 3rd orders of approximation against the numerical results for fixed values of Re = 10, Ha = 200, and α = 5 when η and ϕ are varied. It can be seen, from Table 1, that SHPM results converge rapidly to the numerical solution and similar results achieved between the numerical results and 3rd order of SHPM approximation up to 8 decimal places. Table 2 shows a comparison of HPM and SHPM results at different orders of approximation against the numerical results at selected values of magnetic field and nanoparticle volume fraction for fixed values of Re and α. Convergence of the SHPM is achieved at the 2nd order of approximation up to 8 decimal places as observed in Table 2 even for large values of Ha. In Table 3, we made a comparison between the numerical results, HPM, 10th-order homotopy analysis method [32], and variational iteration method [17] and different order of SHPM of the fluid velocity F(η) and the second derivative F′′(η). The convergence of the SHPM is achieved at the 4th order whereas convergence is not achieved even at the 10th order of HAM approximation. Clearly, SHPM converges at least four times as fast and demonstrates the higher accuracy than HAM, HPM, and VIM. For this reason, SHPM has been used to investigate the effects of physical parameters of the problem. The effect of the magnetic field on the velocity profile is displayed in Figures 2(a) and 2(b) of convergent and divergent channels for fixed values of nanoparticle volume fraction and fixed Reynolds number. The figures indicate that the increase in the Hartmann number leads to increase in the velocity profiles for both convergent and divergent channels which has a great effect on the performance of the system. This is due to the fact that the variation of Ha leads to the variation of the Lorentz force due to the magnetic field, and the Lorentz force produces more resistance to the transport phenomena. Similar result has been reported by [26, 27, 32]. Figure 3 shows the effect of nanoparticle volume fraction on the fluid velocity for fixed Hartmann and Reynolds numbers. It is observed that the fluid velocity increases with the increase in the value of ϕ in the case of diverging channels, and backflow phenomenon is expected for small values of ϕ and large values of Re, while the fluid velocity decreases as the nanoparticle volume fraction increases for the converging channels case. Figure 4 illustrates the effect of increasing Reynolds numbers on the fluid velocity. It was found that, from Figures 4(a) and 4(b) for inflow system, back flow is prevented in the case of convergent channels but is possible for large Reynolds numbers in the case of divergent channels; that is, there is a reverse condition for outflow regime (see [17, 32]).

Table 1. Comparison of the numerical results against the SHPM approximate solutions for F(η) and F′′(η) when Re = 10, Ha = 200, and α = 5.
  η F(η) F′′(η)
  2nd order 3rd order Numerical 2nd order 3rd order Numerical
  ϕ = 0.1 0.0 1 1 1 −1.97361423 −1.97361423 −1.97361423
0.1 0.99013256 0.99013258 0.99013258 −1.97286367 −1.97286367 −1.97286367
0.2 0.96053716 0.96053725 0.96053725 −1.97132614 −1.97132614 −1.97132614
0.3 0.91122738 0.91122758 0.91122758 −1.97114172 −1.97114171 −1.97114172
0.4 0.84220211 0.84220246 0.84220246 −1.97587434 −1.97587434 −1.97587434
0.5 0.75340988 0.75341039 0.75341039 −1.99052431 −1.99052431 −1.99052431
0.6 0.64469883 0.64469947 0.64469947 −2.02157959 −2.02157959 −2.02157959
0.7 0.51575172 0.51575242 0.51575242 −2.07714031 −2.07714032 −2.07714032
0.8 0.36600474 0.36600533 0.36600533 −2.16716308 −2.16716309 −2.16716309
0.9 0.19454749 0.19454782 0.19454782 −2.30388760 −2.30388760 −2.30388760
1.0 0 0 0 −2.50253230 −2.50253230 −2.50253230
  
ϕ = 0.4 0.0 1 1 1 −1.97636754 −1.97636754 −1.97636754
0.1 0.99011749 0.99011749 0.99011749 −1.97717852 −1.97717852 −1.97717852
0.2 0.96046170 0.96046171 0.96046171 −1.97979610 −1.97979610 −1.97979610
0.3 0.91100600 0.91100602 0.91100602 −1.98477509 −1.98477509 −1.98477509
0.4 0.84169981 0.84169985 0.84169985 −1.99304375 −1.99304375 −1.99304375
0.5 0.75245937 0.75245942 0.75245942 −2.00591025 −2.00591025 −2.00591025
0.6 0.64315460 0.64315467 0.64315467 −2.02507402 −2.02507402 −2.02507403
0.7 0.51359211 0.51359218 0.51359218 −2.05264442 −2.05264442 −2.05264442
0.8 0.36349409 0.36349415 0.36349415 −2.09116967 −2.09116967 −2.09116968
0.9 0.19247275 0.19247278 0.19247278 −2.14368045 −2.14368045 −2.14368046
1.0 0 0 0 −2.21375299 −2.21375298 −2.21375298
Table 2. Comparison of the numerical results against the SHPM approximate solutions for F′′(0) when Re = 10 and α = 5.
ϕ Ha SHPM HPM Numerical
1st order 2nd order 3rd order 4th order
0 0 −2.25205783 −2.25205817 −2.25205817 −2.25205817 −2.2522802 −2.25205817
50 −2.18134736 −2.18134748 −2.18134748 −2.18134748 −2.1795097 −2.18134748
100 −2.11325918 −2.11325920 −2.11325920 −2.11325920 −2.1107698 −2.11325920
500 −1.65047007 −1.65046878 −1.65046877 −1.65046877 −1.6734400 −1.65046877
  
0.05 0 −2.21083280 −2.21083294 −2.21083294 −2.21083294 −2.2110158 −2.21083294
50 −2.14969149 −2.14969153 −2.14969153 −2.14969153 −2.1484672 −2.14969153
100 −2.09055197 −2.09055197 −2.09055197 −2.09055197 −2.0889107 −2.09055197
500 −1.68097975 −1.68097904 −1.68097904 −1.68097904 −1.6988408 −1.68097904
  
0.1 0 −2.17511715 −2.17511720 −2.17511720 −2.17511720 −2.1752670 −2.17511720
50 −2.12250597 −2.12250599 −2.12250599 −2.12250599 −2.1217211 −2.12250599
100 −2.07140445 −2.07140446 −2.07140446 −2.07140446 −2.0703633 −2.07140446
500 −1.71124187 −1.71124151 −1.71124151 −1.71124151 −1.7246699 −1.71124151
Table 3. Comparison of the numerical results against the SHPM, HPM, HAM, and VIM approximate solutions for F(η) and F′′(η) when Re = 50, α = 5, Ha = 0, and ϕ = 0.
η HPM Reference [32] Reference [17] SHPM Numerical
2nd order 3rd order 4th order
F(η) 0 1 1 1 1 1 1 1
0.25 0.894960 0.894242 0.894243 0.894238 0.894242 0.894242 0.894242
0.50 0.627220 0.626948 0.626953 0.626937 0.626948 0.626948 0.626948
0.75 0.302001 0.301991 0.301998 0.301982 0.301990 0.301990 0.301990
1 0 0 0 0 0 0 0
  
F′′(η) 0 −3.539214 −3.539417 −3.539369 −3.539546 −3.539416 −3.539416 −3.539416
0.25 −2.661930 −2.662083 −2.662048 −2.662153 −2.662084 −2.662084 −2.662084
0.50 −0.879711 −0.879791 −0.879791 −0.879612 −0.879793 −0.879794 −0.879794
0.75 −0.447331 0.447242 0.447052 0.447350 0.447244 0.447244 0.447244
1 −0.854544 0.854367 0.854440 0.854239 0.854369 0.854369 0.854369
Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Comparison of the numerical results (filled circles) and SHPM approximation for the velocity profile when Re = 50, ϕ = 0.1 and different values of Ha.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Comparison of the numerical results (filled circles) and SHPM approximation for the velocity profile when Re = 50, ϕ = 0.1 and different values of Ha.
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
Comparison of the numerical results (filled circles) and SHPM approximation for the velocity profile when Re = 130, Ha = 50 and different values of ϕ for Cu-water.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
Comparison of the numerical results (filled circles) and SHPM approximation for the velocity profile when Re = 130, Ha = 50 and different values of ϕ for Cu-water.
Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
Comparison of the numerical results (filled circles) and SHPM approximation for the velocity profile when Ha = 200, ϕ = 0.1 and different values of Re.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
Comparison of the numerical results (filled circles) and SHPM approximation for the velocity profile when Ha = 200, ϕ = 0.1 and different values of Re.

6. Conclusion

In this work, we have proposed a modification of the standard homotopy perturbation method for solving nonlinear ordinary differential equations. The method has been used to solve the 3rd-order MHD Jeffery-Hamel flow with nanoparticle. Tables and graphical results are presented to show the accuracy and the convergence rate of the SHPM and to investigate the effects of different physical parameters on the flow as well.

The main conclusions emerging from this study are as follows.
  • (1)

    SHPM is highly accurate, efficient and converges rapidly with a few iterations required to achieve the accuracy of the numerical results compared with the standard HPM. For example, in this study, it was found that only fourth iteration of SHPM was sufficient to give good agreement with the numerical results.

  • (2)

    The method proposes a standard way of choosing the linear operators and initial approximations by using any form of initial guess as long as it satisfies the boundary conditions while the initial guess in the HPM can be selected that will make the integration of the higher-order deformation equations possible.

  • (3)

    The SHPM converges much faster than HPM. For example, in the study above, it was found that the third-order SHPM approximation was sufficient to give good agreement with the numerical results.

  • (4)

    The increase of volume fraction causes an increase in the fluid velocity profile for of diverging channels while the velocity decreases for the converging channels case.

  • (5)

    The fluid velocity increases with increasing Hartman numbers for both diverging and converging channels cases.

Finally, the spectral-homotopy perturbation method described above has high accuracy and is simple for nonlinear boundary value problems compared with the standard homotopy perturbation method. Because of its efficiency and ease of use, the SHPM can also be used to solve nonlinear BVPs in place of the traditional Runge-Kutta methods, finite differences, and Keller-box.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.