The main objective of this paper is to further investigate the exponential stability of a class of impulsive delay differential equations. Several new criteria for the exponential stability are analytically established based on Razumikhin techniques. Some sufficient conditions, under which a class of linear impulsive delay differential equations are exponentially stable, are also given. An Euler method is applied to this kind of equations and it is shown that the exponential stability is preserved by the numerical process.

1. Introduction

Impulsive differential equations arise widely in the study of medicine, biology, economics, engineering, and so forth. In recent years, theory of impulsive differential delay equations (IDDEs) has been an object of active research (see [1–18] and references therein). The results about the existence and uniqueness of IDDEs have been studied in [2, 7]. The stability of IDDEs has attracted increasing interest in both theoretical research and practical applications (see [1, 3, 5–18] and references therein). In particular, special attention has been focused on exponential stability of IDDEs (see [1, 3, 8, 9, 15]) because it has played an important role in many areas.

There is a little work done on exponential stability for IDDEs by the Lyapunov-Razumikhin method. Wang and Liu [15] have extended Lyapunov-Razumikhin method to IDDEs and established some exponential stability criteria. In this paper we restrict the length of each impulsive interval instead of some conditions in [15]. As a result, several new criteria on exponential stability are analytically derived.

There are a few papers on numerical methods of impulsive differential equations. In [19], Covachev et al. obtained a convergent difference approximation for a nonlinear impulsive ordinary system in a Banach space. In [20, 21], the authors studied the stability of Runge-Kutta methods for linear impulsive ordinary differential equations. In [4], Ding et al. studied the convergence property of an Euler method for IDDEs. In [18], asymptotic stability of numerical solutions and exact solutions of a class of linear IDDEs was studied by the property of DDEs without impulsive perturbations. The convergence of the numerical methods for this kind of equations was studied. In this paper, we study exponential stability of the numerical solutions of linear IDDEs.

The rest of the paper is organized as follows. In Section 2, we obtained two criteria on exponential stability for IDDEs by the Lyapunov-Razumikhin method. The results obtained are applied to a class of linear IDDEs. In the last section, we prove that the Euler method for the linear IDDEs preserves the analytic exponential stability.

2. Stability of Analytic Solutions

Consider the impulsive delay differential system

()

where f : R₊ × PC([−τ, 0], R^d) → R^d; I_k : PC([−τ, 0], R^d) → R^d; 0 ≤ t₀ < t₁ < t₂ < ⋯<t_k < ⋯, with t_k → ∞ as k → ∞; PC([−τ, 0], R^d) is a set of piecewise continuous functions g(t) which have a finite number of points of discontinuity in a finite interval and g(t) = g(t⁺) for all t. We assume that f(t, 0) ≡ 0, I_k(t, 0) ≡ 0, so that x ≡ 0 is a solution of (1) as

, which we call the zero solution.

Definition 1 (see [15].)A function V: R₊ × R^d → R₊ is said to belong to the class v₀ if

(i)
V is continuous in each of the sets [t_k−1, t_k) × R^d and for each x ∈ R^d, t ∈ [t_k−1, t_k), exists, k = 1,2, …;
(ii)
V(t, x) is locally Lipschitzian in all x ∈ R^d, and for all t ≥ t₀, V(t, 0) ≡ 0.

Definition 2 (see [15].)Given a function V: R₊ × R^d → R₊, the upper right-hand derivative of V with respect to system (1) is defined by

()

for (t, Ψ) ∈ R₊ × PC([−τ, 0], R^d).

Definition 3 (see [15].)The zero solution of (1) is said to be exponentially stable, if there exist constants λ > 0 and M ≥ 1, such that for any initial data ,

()

Theorem 4. Assume that there exist a function V ∈ v₀; constants d_k > −1, k = 1,2, …; positive constants C₁, C₂, λ, l₁; and a function m(t) ∈ PC ([t₀ − τ, ∞), R₊) with , such that for any Ψ(t) ∈ PC ([−τ, 0], R^d) with Ψ(0⁻) = Ψ(0) the following conditions hold:

(i)
C₁∥x∥ ≤ V(t, x) ≤ C₂∥x∥ for all t ∈ R₊, x ∈ R^d;
(ii)
D⁺V(t, Ψ(0))≤−m(t)V(t, Ψ(0)) for all t ∈ [t_k, t_k+1), whenever for s ∈ [−τ, 0];
(iii)
for k = 1,2, …;
(iv)
t_k − t_k−1 ≥ l₁ for k = 1,2, …, and −λl₁ + ln H₁ < 0, where H₁ = sup _k{1 + d_k}.

Then the zero solution of (1) is exponentially stable.

Proof. Similar to the proof of Theorem 3.1 in [15], we obtain that

()

Since −λl₁ + ln H₁ < 0, there exists α such that 0 < α < λ and −(λ − α)l₁ + ln H₁ < 0. So

()

Hence the zero solution of (1) is exponentially stable.

Remark 5. Theorem 3.1 in [15] requires that d_i ≥ 0, and , which implies lim _k→∞d_k = 0. In our Theorem 4, we require t_k − t_k−1 ≥ l₁ for k = 1,2, …, and instead. This means that the impulsive effects are bounded instead of tending to zero (see Example 13).

Theorem 6. Assume that there exist a function V ∈ v₀; constants d_k ∈ (−1,0), k = 1,2, …; positive constants l₁, l₂, C₁, C₂, λ; and a function m(t) ∈ PC ([t₀ − τ, ∞), R₊) with , such that for any Ψ(t) ∈ PC ([−τ, 0], R^d) with Ψ(0⁻) = Ψ(0), the following conditions hold:

(i)
C₁∥x∥ ≤ V(t, x) ≤ C₂∥x∥ for all t ∈ R₊, x ∈ R^d;
(ii)
D⁺V(t, Ψ(0)) ≤ m(t)V(t, Ψ(0)) for all t ∈ [t_k, t_k+1), k = 1,2, …, whenever V(t, Ψ(0)) ≥ γV(t + s, Ψ(s)) for s ∈ [−τ, 0], where γ is a constant and , H₂ = inf _k{1 + d_k} and q is the smallest integer larger than or equal to τ/l₁;
(iii)
;
(iv)
l₁ ≤ t_k − t_k−1 ≤ l₂ for k = 1,2, …, and , where H₁ = sup _k{1 + d_k}, H₂ = inf _k{1 + d_k}.

Then the zero solution of (1) is exponentially stable.

Proof. Let x(t) = x(t, t₀, Φ) be the solution of system (1) and V(t) = V(t, x(t)). We will prove

()

Let

()

We need to show that Q(t) ≤ 0 for all t ≥ t₀. It is clear that Q(t) ≤ 0 for t ∈ [t₀ − τ, t₀], since Q(t) = V(t) − C₂∥Φ∥_τ ≤ 0 by condition (i).

Next we shall show Q(t) ≤ 0, for t ∈ [t₀, t₁). Suppose this is not true. Then there is a t^* such that t^* ≤ inf {t ∈ [t₀, t₁), Q(t) > 0}, Q(t^*) ≤ 0, Q(t^*) ≥ (γ − 1)C₂∥Φ∥_τ, and

()

Note that

. Then

for s ∈ [−τ, 0]. By condition (ii), D⁺V(t^*) ≤ m(t^*)V(t^*). So

()

which contradicts (8). Hence Q(t) ≤ 0, for all t ∈ [t₀, t₁).

Assume that Q(t) ≤ 0, for t ∈ [t₀, t_m), m ≥ 1. We shall show that Q(t) ≤ 0, for t ∈ [t₀, t_m+1). Obviously, by condition (iii)

()

Suppose that there exists a t such that t ∈ [t_m, t_m+1) and Q(t) > 0. There is a t^* such that t^* ≤ inf {t ∈ [t_m, t_m + 1), Q(t) > 0}, Q(t^*) ≤ 0,

, and

()

Since , then for any s ∈ [−τ, 0], we have

()

Thus by condition (ii), D⁺V(t^*) ≤ m(t^*)V(t^*), then

()

which contradicts (11). Hence Q(t) ≤ 0 for all t ∈ [t_m, t_m+1). By induction, Q(t) ≤ 0 for all t ≥ t₀. In view of m(t) ≤ λ for all t ≥ t₀ − τ, we obtain

()

for t ∈ [t_k, t_k+1), k = 1,2, …. Since

, there exists α such that 0 < α < λ and λl₂ + ln H₂ < −αl₂. By condition (i)

()

where

. Hence the zero solution of (1) is exponentially stable.

Remark 7. Theorem 6 says that the delay differential equation is unstable and the suitable impulse effects are given, then it will become stable (see Example 14). Compared with the Theorem 3.1 in [16], we do not require that τ ≤ t_k − t_k−1. For example, by Theorem 6 we know that the zero solution of the following system is exponentially stable:

()

In the following we consider

()

where τ > 0, and d_k, a, b ∈ R are constants.

Theorem 8. Assume that c_k ≠ −1, k = 1,2, …, and there is a constant λ > 0 such that a+|b | e^λτ ≤ −λ and 0 < H₁ < e^λτ, where H₁ = sup _k{|1 + c_k|}. Then the zero solution of (17) is exponentially stable.

Proof. Assume that V(x) = V(t, x) = |x|.

(i)
Obviously, there exist C₁ = C₂ = 1, such that C₁ | x | ≤ V(x) ≤ C₂ | x|.
(ii)
Assume that m(t) = λ for all t ≥ −τ. For any Ψ ∈ PC([−τ, 0], R), if
()

we have |Ψ(−τ)| ≤ e^λτ | Ψ(0)|. For s ∈ [−τ, 0], we have

()

(iii)
Suppose that 1 + d_k = |(1 + c_k)|. Hence
()
(iv)
Obviously, l₁ = τ = t_k − t_k−1 and −λl₁ + ln H₁ < 0.

By Theorem 4, the zero solution of (11) is exponentially stable.

Similarly, by Theorem 6 we have the following theorem.

Theorem 9. Assume that 0<|1 + c_k | < 1, k = 1,2, …, and there are constants λ and γ such that λ > 0, 0 < γ < H₂ ≤ H₁ < e^−λτ, and a+|b | γ⁻¹ ≤ λ, where H₁ = sup _k{|1 + c_k|}, H₂ = inf _k{|1 + c_k|}. Then the zero solution of (17) is exponentially stable.

3. The Euler Method for Linear IDDEs

In this section, we consider the exponential stability of the Euler method for (17). The convergence property can be proved similarly to [4]. The Euler method for (17) with initial function Φ ∈ PC([−τ, 0], R) is given by

()

where h = τ/m. Let n = km + l, then x_n = x_km+l = x_k,l is an approximation for the exact solution x((km + l)h) for k = 0,1, 2, …, l = 0,1, 2, …, m − 1, and x_k,m is an approximation for x((k + 1)τ⁻).

Definition 10. The Euler method for (11) is said to be exponentially stable if there exist positive constants λ, M, and M₁, for any Φ ∈ PC ([−τ, 0], R), such that ∥x_n∥ ≤ M∥Φ∥_τe^−nλh for h = τ/m, m ≥ M₁, and n = 1,2, ….

The following theorem indicates that the Euler method preserves the property of exact solutions which was obtained above.

Theorem 11. Under the conditions of Theorem 8, the Euler method for (17) is exponentially stable.

Proof. If a < 0, then M₁ = −aτ. (i) If H₁ > 1, we want to prove that

()

for k = 0,1, 2, …, l = 0,1, 2, …, m. Obviously, |x_0,0 | = |Φ(0)| ≤ ∥Φ∥_τ. Firstly, we consider the case k = 0 and l = 1. Because h = τ/m and m ≥ M₁, so 1 + ha ≥ 0. Hence we have

()

Because a + |b|e^λτ ≤ −λ, we have |x_0,1| ≤ (1 − hλ)∥Φ∥_τ. By the inequality e^−x ≥ 1 − x holding for all x ∈ R, we get |x_0,1| ≤ ∥Φ∥_τe^−λh.

Assume that |x_0,p| ≤ ∥Φ∥_τe^−λph for p < l ≤ m. Then

()

So (22) holds for k = 0, l = 0,1, 2, …, m. Suppose that (22) holds for n < k, l = 0,1, 2, …, m. Next, we shall prove (22) holds, when n = k, l = 0,1, 2, …, m. Hence

()

Assume that

for u < l ≤ m. Then

()

Hence (22) holds. Since −λl₁ + ln H₁ < 0, there exists α such that 0 < α < λ and −(λ − α)l₁ + ln H₁ < 0. Hence

()

(ii)
If H₁ ≤ 1, we can prove that
()

Consequently, the theorem holds.

Theorem 12. Under the conditions of Theorem 9, the Euler method for (17) is exponentially stable.

Example 13. Consider the system

()

Obviously, λ = 1 satisfies the Theorem 8. Therefore the zero solution of (29) is exponentially stable. By Theorem 11, the Euler method for (29) is also exponentially stable (see Figure 1).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The solutions of (29), as Φ ≡ 1, h = 1/10.

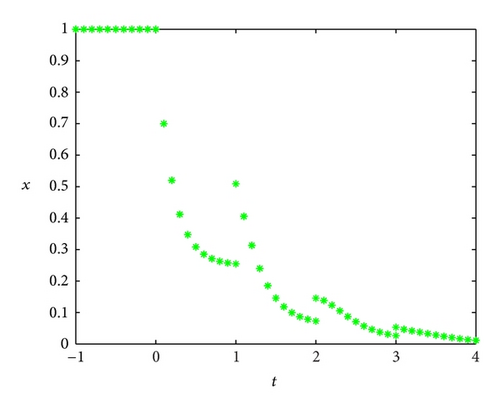
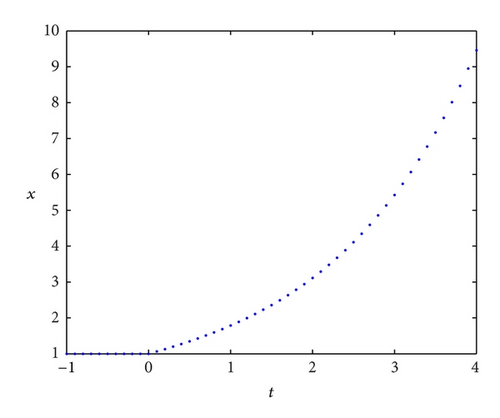
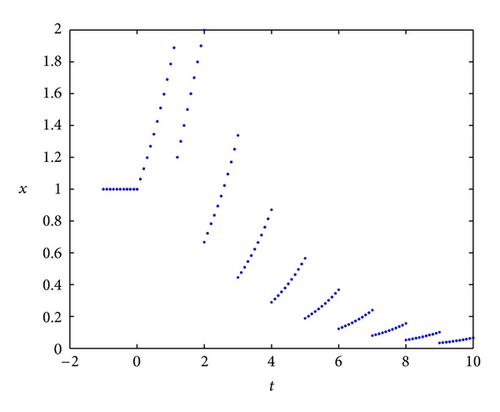
Example 14. Obviously, the zero solution of the system

()

is unstable (see Figure 2) while the zero solution of the following system

()

is exponentially stable by Theorem 9 with λ = 1. By Theorem 12, the Euler method for (31) is also exponentially stable (see Figure 3).

Acknowledgments

The authors wish to thank referees for valuable comments. The research was supported by the NSF of China no. 11071050.

References

1 Anokhin A., Berezansky L., and Braverman E., Exponential stability of linear delay impulsive differential equations, Journal of Mathematical Analysis and Applications. (1995) 193, no. 3, 923–941, https://doi.org/10.1006/jmaa.1995.1275, MR1341049, ZBL0837.34076.
10.1006/jmaa.1995.1275
Web of Science® Google Scholar
2 Ballinger G. and Liu X., Existence and uniqueness results for impulsive delay differential equations, Dynamics of Continuous, Discrete and Impulsive Systems. (1999) 5, no. 1–4, 579–591, MR1678279, ZBL0955.34068.
Google Scholar
3 Berezansky L. and Idels L., Exponential stability of some scalar impulsive delay differential equations, Communications in Applied Analysis. (1998) 2, no. 3, 301–308, MR1626697, ZBL0901.34068.
Google Scholar
4 Ding X., Wu K., and Liu M., The Euler scheme and its convergence for impulsive delay differential equations, Applied Mathematics and Computation. (2010) 216, no. 5, 1566–1570, https://doi.org/10.1016/j.amc.2010.03.007, MR2629958, ZBL1202.65088.
10.1016/j.amc.2010.03.007
Web of Science® Google Scholar
5 De La Sen M. and Luo N., A note on the stability of linear time-delay systems with impulsive inputs, IEEE Transactions on Circuits and Systems. I. (2003) 50, no. 1, 149–152, https://doi.org/10.1109/TCSI.2002.807514, MR1965731.
10.1109/TCSI.2002.807514
Web of Science® Google Scholar
6 De la Sen M., Stability of impulsive time-varying systems and compactness of the operators mapping the input space into the state and output spaces, Journal of Mathematical Analysis and Applications. (2006) 321, no. 2, 621–650, https://doi.org/10.1016/j.jmaa.2005.08.038, MR2241144, ZBL1111.93072.
10.1016/j.jmaa.2005.08.038
Web of Science® Google Scholar
7 Liu X., Stability results for impulsive differential systems with applications to population growth models, Dynamics and Stability of Systems. (1994) 9, no. 2, 163–174, MR1287514, https://doi.org/10.1080/02681119408806175, ZBL0808.34056.
10.1080/02681119408806175
Web of Science® Google Scholar
8 Liu X., Shen X., and Zhang Y., Exponential stability of singularly perturbed systems with time delay, Applicable Analysis. (2003) 82, no. 2, 117–130, https://doi.org/10.1080/0003681031000063775, MR1966852, ZBL1044.34031.
10.1080/0003681031000063775
Google Scholar
9 Liu X. and Wang Q., The method of Lyapunov functionals and exponential stability of impulsive systems with time delay, Nonlinear Analysis: Theory, Methods & Applications. (2007) 66, no. 7, 1465–1484, https://doi.org/10.1016/j.na.2006.02.004, MR2301332, ZBL1123.34065.
10.1016/j.na.2006.02.004
Web of Science® Google Scholar
10 Liu X., Shen X., Zhang Y., and Wang Q., Stability criteria for impulsive systems with time delay and unstable system matrices, IEEE Transactions on Circuits and Systems. I. (2007) 54, no. 10, 2288–2298, https://doi.org/10.1109/TCSI.2007.904592, MR2460427.
10.1109/TCSI.2007.904592
Web of Science® Google Scholar
11 Luo Z. and Shen J., Stability of impulsive functional differential equations via the Liapunov functional, Applied Mathematics Letters. (2009) 22, no. 2, 163–169, https://doi.org/10.1016/j.aml.2008.03.004, MR2482270.
10.1016/j.aml.2008.03.004
Web of Science® Google Scholar
12 Stamova I. M. and Stamov G. T., Lyapunov-Razumikhin method for impulsive functional differential equations and applications to the population dynamics, Journal of Computational and Applied Mathematics. (2001) 130, no. 1-2, 163–171, https://doi.org/10.1016/S0377-0427(99)00385-4, MR1827978, ZBL1022.34070.
10.1016/S0377-0427(99)00385-4
Web of Science® Google Scholar
13 Shen J. H., Razumikhin techniques in impulsive functional-differential equations, Nonlinear Analysis: Theory, Methods & Applications. (1999) 36, no. 1, 119–130, https://doi.org/10.1016/S0362-546X(98)00018-2, MR1670339, ZBL0939.34071.
10.1016/S0362-546X(98)00018-2
Web of Science® Google Scholar
14 Shen J. and Yan J., Razumikhin type stability theorems for impulsive functional-differential equations, Nonlinear Analysis: Theory, Methods & Applications. (1998) 33, no. 5, 519–531, https://doi.org/10.1016/S0362-546X(97)00565-8, MR1635724, ZBL0933.34083.
10.1016/S0362-546X(97)00565-8
Web of Science® Google Scholar
15 Wang Q. and Liu X., Exponential stability for impulsive delay differential equations by Razumikhin method, Journal of Mathematical Analysis and Applications. (2005) 309, no. 2, 462–473, https://doi.org/10.1016/j.jmaa.2004.09.016, MR2154129, ZBL1084.34066.
10.1016/j.jmaa.2004.09.016
Web of Science® Google Scholar
16 Wang Q. and Liu X., Impulsive stabilization of delay differential systems via the Lyapunov-Razumikhin method, Applied Mathematics Letters. (2007) 20, no. 8, 839–845, https://doi.org/10.1016/j.aml.2006.08.016, MR2323119, ZBL1159.34347.
10.1016/j.aml.2006.08.016
Web of Science® Google Scholar
17 Zhang Y. and Sun J., Stability of impulsive functional differential equations, Nonlinear Analysis: Theory, Methods & Applications. (2008) 68, no. 12, 3665–3678, https://doi.org/10.1016/j.na.2007.04.009, MR2416074, ZBL1152.34053.
10.1016/j.na.2007.04.009
Web of Science® Google Scholar
18 Zhang G. L., Song M. H., and Liu M. Z., Asymptotical stability of a class impulsive delay differential equations, Journal of Applied Mathematics. (2012) 2012, 9, 723893.
10.1155/2012/723893
Google Scholar
19 Covachev V., Akça H., and Yeniçerioğlu F., Difference approximations for impulsive differential equations, Applied Mathematics and Computation. (2001) 121, no. 2-3, 383–390, https://doi.org/10.1016/S0096-3003(00)00014-X, MR1830880, ZBL1024.65065.
10.1016/S0096-3003(00)00014-X
Web of Science® Google Scholar
20 Liu M. Z., Liang H., and Yang Z. W., Stability of Runge-Kutta methods in the numerical solution of linear impulsive differential equations, Applied Mathematics and Computation. (2007) 192, no. 2, 346–357, https://doi.org/10.1016/j.amc.2007.03.044, MR2385600, ZBL1193.65121.
10.1016/j.amc.2007.03.044
Web of Science® Google Scholar
21 Ran X. J., Liu M. Z., and Zhu Q. Y., Numerical methods for impulsive differential equation, Mathematical and Computer Modelling. (2008) 48, no. 1-2, 46–55, https://doi.org/10.1016/j.mcm.2007.09.010, MR2431322, ZBL1145.65317.
10.1016/j.mcm.2007.09.010
Google Scholar

Citing Literature

All articles

Exponential Stability of Impulsive Delay Differential Equations

Abstract

1. Introduction

2. Stability of Analytic Solutions

3. The Euler Method for Linear IDDEs

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Exponential Stability of Impulsive Delay Differential Equations

Abstract

1. Introduction

2. Stability of Analytic Solutions

3. The Euler Method for Linear IDDEs

Acknowledgments

References

Citing Literature

Figures

References

Related

Information