For solving Laplace’s equation in circular domains with circular holes, the null field method (NFM) was developed by Chen and his research group (see Chen and Shen (2009)). In Li et al. (2012) the explicit algebraic equations of the NFM were provided, where some stability analysis was made. For the NFM, the conservative schemes were proposed in Lee et al. (2013), and the algorithm singularity was fully investigated in Lee et al., submitted to Engineering Analysis with Boundary Elements, (2013). To target the same problems, a new interior field method (IFM) is also proposed. Besides the NFM and the IFM, the collocation Trefftz method (CTM) and the boundary integral equation method (BIE) are two effective boundary methods. This paper is devoted to a further study on NFM and IFM for three goals. The first goal is to explore their intrinsic relations. Since there exists no error analysis for the NFM, the second goal is to drive error bounds of the numerical solutions. The third goal is to apply those methods to Laplace’s equation in the domains with extremely small holes, which are called actually punctured disks. By NFM, IFM, BIE, and CTM, numerical experiments are carried out, and comparisons are provided. This paper provides an in-depth overview of four methods, the error analysis of the NFM, and the intriguing computation, which are essential for the boundary methods.

1. Introduction

For circular domains with circular holes, there exist a number of papers of boundary methods. In Barone and Caulk [1, 2] and Caulk [3], the Fourier functions are used for the circular holes for boundary integral equations. In Bird and Steele [4], the simple algorithms as the collocation Trefftz method (CTM) in [5, 6] are used. In Ang and Kang [7], complex boundary elements are studied. Recently, Chen and his research group have developed the null filed method (NFM), in which the field nodes Q are located outside of the solution domain S. The fundamental solutions (FS) can be expanded as the convergent series, and the Fourier functions are also used to approximate the Dirichlet and Neumann boundary conditions. Numerous papers have been published for different physical problems. Since error analysis and numerical experiments for four boundary methods are our main concern, we only cite [8–14]. More references of NFM are also given in [10–12, 14–17].

In [17], explicit algebraic equations of the NFM are derived, stability analysis is first made for the simple annular domain with concentric circular boundaries, and numerical experiments are performed to find the optimal field nodes. The field nodes can be located on the domain boundary: Q ∈ ∂S, if the solutions are smooth enough to satisfy u ∈ H²(∂S) and u_ν ∈ H¹(∂S), where u_ν is the normal derivative and H^k(∂S) (k = 1,2) are the Sobolev spaces; see the proof in [17]. It is discovered numerically that when the field nodes Q ∈ ∂S, the NFM provides small errors and the smallest condition numbers, compared with all Q ∈ S^c. Moreover for the NFM, the conservative schemes are proposed in [15], and the algorithm singularity is fully investigated in [16]. In fact, the explicit algebraic equations can also be derived from the Green representation formula with the field nodes inside the solution domain. This method is called the interior field method (IFM).

In addition to the NFM and IFM, the collocation Trefftz method (CTM) and the boundary integral equation method (BIE) are effective boundary methods too. Three goals are motivated in this paper. The first goal is to explore the intrinsic relations of NFM, IFM, CTM, and BIE with an in-depth overview. So far, there exists no error analysis for the NFM. The second goal is to derive error bounds of the numerical solutions by the NFM. The optimal convergence (or exponential) rates can be achieved. The third goal is to solve a challenging problem: Laplace′s equation in the circular domains with extremely small holes, which are called the actually punctured disks in this paper. Four boundary methods, NFM, IFM, CTM, and BIE, are employed. Numerical experiments are carried out, and comparisons are provided. It is observed that the CTM is more advantageous in the applications than the others.

Besides, the method of fundamental solutions (MFS) is also popular in boundary methods, which originated from Kupradze and Aleksidze [18] in 1964. For the MFS, numerous computations are reviewed in Fairweather and Karageorghis [19] and Chen et al. [20], but the error and stability analysis is developed by Li et al. in [21, 22]. Both the CTM and the MFS can be applied to arbitrary solution domains. However, the MFS incurs a severe numerical instability for very elongated domains [22]. Since the performance of the CTM is better than that of the MFS, reported elsewhere, we do not carry out the numerical computation of the MFS in this paper. Moreover, the null-field method with discrete source (NFM-DS) is effective and popular in light scattering (see Wriedt [23]), where the transition (T) matrix is provided in Doicu and Wriedt [24]. In fact, the null field equation (NFE) of the Green representation formula in (9) can be employed on a source outside the solution domain S, without a need of the FS expansions, called the T matrix method [24]. Hence, the T matrix method is valid for arbitrary solution domains. There also occurs a severe numerical instability for very elongated holes (i.e., particles). To improve the stability for this case, different sources (i.e., discrete sources) may be utilized in the NFM-DS, by means of the idea of the MFS. The techniques for improving the stability by the NFM-DS are reported in many papers; we only cite [23, 25].

This paper is organized as follows. In the next section, the explicit discrete equations of NFM, IFM, CTM, and BIE are given, and their relations and overviews are explored. In Section 3, for the NFM some analysis is studied for circular domains with concentric circular boundaries. In Section 4, error bounds are provided without proof for the NFM with eccentric circular boundaries of simple annular domains. In Section 5, numerical experiments are carried out for Laplace′s equation in the actually punctured disks. The results are reported with comparisons. In the last section, a few concluding remarks are addressed.

2. The Null Field Method and Other Algorithms

2.1. The Null Field Method

For simplicity in description of the NFM, we confine ourselves to Laplace′s equation and choose the circular domain with one circular hole in this paper. Denote the disks S_R and

with radii R and R₁, respectively. Let

, and the eccentric circular domains S_R and

may have different origins. Hence 2R₁ < R. Choose the annular solution domain

with the exterior and the interior boundaries ∂S_R and

, respectively. The following Dirichlet problems are discussed by Palaniappan [26]:

()

In [11], R = 2.5 and R₁ = 1 and the origins of S_R and

are located at (0,0) and (−R₁, 0), respectively. In this paper, we fix R = 2.5, while R₁ may be infinitesimal; that is, R₁ ≪ 1.

On the exterior boundary ∂S_R, there exist the approximations of Fourier expansions:

()

where a_k, b_k, p_k, and q_k are coefficients. On the interior boundary

, we have similarly

()

where

, and

are coefficients. In (2)–(5), θ and

are the polar coordinates of S_R and

with the origins (0,0) and (−R₁, 0), respectively, and ν and

are the exterior normals of ∂S_R and

, respectively. The Dirichlet, the Neumann conditions, and their mixed types on ∂S_R may be given with known coefficients.

In S, denote two nodes x = Q = (x, y) = (ρ, θ) and y = P = (ξ, η) = (r, ϕ), where x = ρcos θ, y = ρsinθ, ξ = rcos ϕ, and η = rsinϕ. Then

and

. The FS of Laplace′s equation is given by

. From the Green representation formula, we have different formulas for different locations of the field nodes Q(x):

()

where P(y)∈(S ∪ ∂S) and two kinds of series expansions of the FS ln | PQ| are given by (see [27])

()

where x = (ρ, θ) and y = (r, ϕ). Then we have two kinds of derivative expansions of FS

()

where the superscripts “e” and “i” designate the exterior and interior field nodes x, respectively. Note that the boundary element method (BEM) is based on the second equation of the Green formula (6), but the NFM is based on the third equation (i.e., the null field equation (NFE)) by using the FS expansions. We have

()

where

is the complementary domain of S ∪ ∂S. Substituting the Fourier expansions (7)–(8) into (9) yields the basic algorithms of NFM, where the exterior normal of

is given by ∂U(x, y)/∂ν = −∂U(x, y)/∂r. In the Green formula (9), the field point x = (ρ, θ) is supposed to locate outside of the solution domain S ∪ ∂S only, so the algorithm of Chen is called the null field method (NFM) [8, 9, 11]. The field nodes can also be located on the domain boundary: Q ∈ ∂S, if the solutions are smooth enough to satisfy u ∈ H²(∂S) and u_ν ∈ H¹(∂S), where u_ν is the normal derivative and H^k(∂S) (k = 1,2) are the Sobolev spaces; see the rigorous proof in [17]. It is discovered numerically that when the field nodes Q ∈ ∂S, the NFM provides small errors and condition numbers and has been widely implemented in many engineering problems.

Denote two systems of polar coordinates by (ρ, θ) and

with the origins (0,0) and (x₁, y₁) for S_R and

, respectively. There exist the following conversion formulas:

()

First, consider the exterior field nodes x = (ρ, θ) with ρ > r = R. The first explicit algebraic equations of the NFM are given for the exterior field nodes (see [17])

()

Next, consider the interior field nodes

with

. The second explicit algebraic equations of the NFM are given for the interior field nodes (see [17])

()

Since one of Dirichlet or Neumann conditions is given on ∂S_R and

, only 2(M + N) + 2 coefficients in (2)–(5) are unknowns. We choose 2M + 1 and 2N + 1 field nodes located uniformly on the exterior and the interior circles, respectively,

()

where ϵ ≥ 0,

, Δθ = 2π/(2M + 1), and

. Denote the explicit equations (12) and (13) by

()

We obtain 2(M + N) + 2 discrete equations from (15)

()

where the corresponding coordinates (ρ_i, θ_i) and

are obtained from (10) and (11). Hence from (16), we obtain the following linear algebraic equations:

()

where the matrices F(∈R^n×n), the vector x(∈Rⁿ), and n = 2(M + N) + 2. The unknown coefficients can be obtained from (17), if the matrix F is nonsingular. In this paper, we confine the Dirichlet problems. The study of the Neumann problems will be reported in a subsequent paper.

Once all the coefficients are known, based on the first equation of the Green formula (6), the solution at the interior nodes: x = (ρ, θ) ∈ S is expressed by

()

For (ρ, θ) ∈ S, from (2)–(5) and (7)-(8), (2.20) leads to (see [17])

()

where

are also given from (11).

2.2. Conservative Schemes

For some physical problems, the flux conservation is imperative and essential. The conservative schemes of NFM can be designed to satisfy exactly the flux conservation [15]

()

Substituting (3) and (5) into (20) yields directly

()

We may use (21) to remove one coefficient, say

()

By using (22), (12) and (13) lead to

()

Also the interior solution (19) leads to

()

Hence, the total number of unknown coefficients is reduced to 2(M + N) + 1. Based on the analysis in [15], to remain good stability, we still choose 2(M + N) + 2 collocation nodes as in (16):

()

where the weights w₀ = 1,

for i ≥ 1, Δθ = 2π/(2M + 1), and

. Equation (25) form an overdetermined system, which can be solved by the QR method or the singular value decomposition.

2.3. The Interior Field Method

In [17], we prove that when u ∈ H²(∂S) and u_ν ∈ H¹(∂S), the NFM remains valid for the field nodes Q ∈ ∂S; that is, ρ = R on ∂S_R and on and (23) and (24) hold. In fact, we may use (24) only, because (23) is obtained directly from the Dirichlet conditions on ∂S_R and , respectively. Interestingly, (24) is obtained from the interior (i.e., the first) Green formula in (6) only. For this reason, the interior field method (IFM) is named. Evidently, the IFM is equivalent to the special NFM. Based on this linkage, the new error analysis in Section 4 is explored.

2.4. The First Kind Boundary Integral Equations

We may also apply the series expansions of FS to the first kind boundary integral equations. Consider the Dirichlet problem

()

where |x| is the Euclidean distance. In (26),

is an open arc, and each of its edges, Γ_m (m = 1, …, d), is assumed to be smooth. Let C_Γ be the logarithmic capacity of Γ. From the single layer potential theory [28–30], if C_Γ ≠ 1, (26) can be converted to the first kind boundary integral equation (BIE),

()

where v(x)( = (∂u(x)/∂n⁻)−(∂u(x)/∂n⁺)) is the unknown function and ∂u/∂n^± denote the normal derivatives along the positive and negative sides of Γ. If C_Γ ≠ 1, there exists a unique solution of (27), see [28]. As soon as v(x) is solved from (27), the solution u(x) (x ∈ Ω) of (26) can be evaluated by

()

For the smooth solution u, we have v(x) = 2(∂u/∂ν), where ν is the normal of Γ. We may assume the Fourier expansions of v on Γ

()

where

, and

are the coefficients. We have from [17]

()

to give

()

Note that the derivation of (31) in the first kind BIE is simpler, because we do not need the series expansions of ∂Uⁱ(x, y)/∂r and ∂U^e(x, y)/∂r. This advantage is very important for elasticity problems, because the displacement conditions are much simpler than the traction ones.

2.5. The Collocation Trefftz Method

We also use the collocation Trefftz method (CTM). For (1), the particular solutions of CTM are given by (see [6])

()

where

, and

are the coefficients. Evidently, the admissible functions (19) of the IFM and (31) of the first kind BIE are the special cases of (32). Equation (31) may be written as (32) with the following relations of coefficients:

()

Equation (19) can also be written as (32) with

()

where

are the coefficients in (19) of the IFM.

Therefore, we may classify the IFM and the first kind BIE into the TM family, and their analysis may follow the framework in [6]. However, the particular solutions (32) can be applied to arbitrary shaped domains, for example, simply or multiple-connected domains, but the functions (19) and (31) are confined themselves to the circular domains with circular holes only. The four boundary methods, NFM, IFM, BIE, and CTM, are described together, with their explicit algebraic equations. The relations of their expansion coefficients are discovered at the first time. Moreover, Figure 1 shows clear relations among NFM, IFM, BIE, and CTM. The intrinsic relations have been provided to fulfill the first goal of this paper.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Relations among NFM, IFM, BIE, and CTM.

To close this section, we describe the CTM. Denote V_M−N the set of (32), and define the energy

()

where Γ = ∂S and f is the known function of Dirichlet boundary conditions. Then the solution u_M−N of the Trefftz methods (TM) can be obtained by

()

The TM solution u_M−N also satisfies

()

When the integral in (35) involves numerical approximation, the modified energy is defined as

()

where

is the numerical approximations of ∫_Γ by some quadrature rules, such as the central or the Gaussian rule. Hence, the numerical solution

is obtained by

()

We may also establish the collocation equations directly from the Dirichlet condition to yield

()

Following [6], (40) is just equivalent to (38).

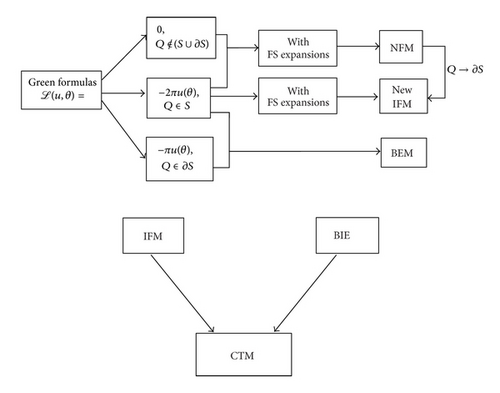
3. Preliminary Analysis of the NFM

In this section, a preliminary analysis of the NFM is made for concentric circular boundaries. In the next section, error analysis of the NFM with

is explored for eccentric circular boundaries. Consider the simple domains of

, where S_R and

have the same origin. For the same origin O of S_R and

, the same polar coordinates (ρ, θ) are used, and the general solutions in

can be denoted by

()

where

are true coefficients and R₁ ≤ ρ ≤ R. Then their derivatives are given by

()

When ρ = R, from (41) and (42), we have

()

Comparing (43) with (2) and (3), we have the following equalities of coefficients:

()

where a_k, b_k, p_k, and q_k are the coefficients of the NFM in Section 2.1.

Also, when ρ = R₁, from (41) and (42), we have

()

Comparing (46) with (4) and (5), we have

()

where

, and

are also the coefficients of the NFM in Section 2.1.

On the other hand, when

, we have from the first original equation (12)

()

Then for ρ ≥ R, we obtain the following equalities, based on the orthogonality of trigonometric functions:

()

Similarly, from the second equation (13),

()

Then for ρ ≤ R₁, we obtain

()

Below, we prove that the true coefficients can be obtained directly from the NFM based on (50)–(52) for ρ ≥ R and on (54)–(56) for ρ ≤ R₁. Outline of the proof is as follows. We will prove that the true solutions satisfy (50)–(52) and (54)–(56) of the NFM. Based on the analysis in [16], when R ≠ 1, there exists a unique solution of the special NFM with

. Therefore, the true coefficients can be determined by the IFM uniquely.

First to show (50). The consistent condition is given by

()

Equation (57) can also be obtained from (45) and (48). Equations (57) and (50) are equivalent if ln ρ ≠ 0 (i.e., ρ ≠ 1), which is also the necessary condition of nonsingularity of matrix F in (17) [16]. Based on (57), the conservative schemes are proposed in [15]. Equation (54) is shown next. We have from (44) and (47)

()

where we have used (45) and (48).

Equations (51) and (55) are shown below. Denote them in matrix form

()

and denote from (44) and (47)

()

where

and

are true expansion coefficients. Also denote from (45) and (48)

()

By substituting (60) and (61) into (59), its left-hand side leads to

()

The right-hand side of (59) leads to

()

The second equality of the right-hand sides of (62) and (63) yield (59). The proof for the validity of (52) and (56) is similar. We write these important results as a proposition.

Proposition 1. For the concentric circular domains, when ρ = R + ϵ ≠ 1, the leading coefficients are exact by the NFM, and the solution errors result only from the truncations of their Fourier expansions.

4. Error Bounds of the NFM with

The NFM with the field nodes Q ∈ ∂S (i.e., ) located on the domain boundary is the most important application for Chen′s publications (see [8–14]). We will provide the errors bounds under the Sobolev norms of this special NFM for circular domains with eccentric circular boundaries without proof. Based on the equivalence of the special NFM and the CTM, we may follow the framework of analysis of Treffez method in [6]. The Sobolev norms for Fourier functions are provided in Kreiss and Oliger [31], Pasciak [32], and Canuto and Quarteroni [33].

Let the domain S be divided into two subdomains S^ext and S^int with an interface boundary Γ₀ ∈ S. We have S = S^ext ∪ S^int ∪ Γ₀ and S^ext∩S^int = ∅, where ∂S^ext = ∂S_R ∪ Γ₀ and

. We assume that the true solutions have different regularities

()

where p ≥ 2 and σ ≥ 2. Then there are different regularities on the boundary

()

where ν and

are the exterior normal to ∂S^ext and ∂S^int, respectively. Therefore, the true solutions can be expressed by the Fourier expansions on ∂S_R

()

where

, are the true boundary coefficients. Similarly, we have

()

where

, are the true boundary coefficients.

Denote finite terms of the Fourier expansions on ∂S_R in (66) and (67) by

()

also denote the circle ℓ_r = {(ρ, θ)∣ρ = r, 0 ≤ θ ≤ 2π}. For ∂S_R = ℓ_R, for the solution (66), the Sobolev norms are defined as

()

We have the following lemma, whose proof can be found in Canuto et al. [33, 34].

Lemma 2. Let (64) be given, for ∂S_R = ℓ_R; there exist the bounds of the remainders of (69)

()

where C is a constant independent of M.

Also denote the finite terms of the Fourier expansions on

in (68) by

()

We can prove the following lemma similarly.

Lemma 3. Let (64) be given, for ; there exist the bounds of the remainders of (72)

()

where C is a constant independent of N.

We have the following theorem.

Theorem 4. Let (64) and R ≠ 1 hold. For the solution u_N,M from the TM in (36), there exists the error bound

()

where C is a constant independent of N and M.

Next, we study the errors of the interpolant solutions from (16) of the NFM with

()

where the uniform nodes Δθ = 2π/(2M + 1) and

. Equation (75) is equivalent to

()

where u₀ and

are given in (2) and (4). We have the following theorem.

Theorem 5. Let (64) and R ≠ 1 hold. For the NFM with and the uniform nodes, the interpolant solutions from (76) have the same error bound of (74)

()

where C is a constant independent of N and M.

5. Numerical Experiments

5.1. IFM and Its Conservative Schemes

In this paper, we choose the NFM with

, which is equivalent to the IFM, and its conservative schemes of [15]. For (1) with symmetry, the explicit interior solution (24) is simplified as

()

In [17], when u ∈ H²(S), we may choose the field nodes to be located on the solution boundary for (78): (ρ, θ) ∈ ∂S_R and

. Then we obtain two boundary equations of the conservative schemes of the IFM from (78), (2), and (4)

()

The coefficients

are unknowns, and the total number of unknowns is M + N + 1. Based on [15], to bypass the pseudosingularity, we still choose M + N + 2 equations from (79)

()

where ϵ ≥ 0,

, Δθ = 2π/(2M + 1) and

. The weights w₀ = 1 and

are defined for i ≥ 1, based on the stability analysis in [17]. The overdetermined system of (80) is denoted by the linear algebraic equations

()

where F ∈ R^m×n with n = M + N + 1 and m = M + N + 2. The traditional condition number and the effective condition number in [35] are defined by

()

where σ_max and σ_min are the maximal and the minimal singular values of the matrix F in (81), respectively.

Next, we use the original IFM (i.e., the original NFM with

). The particular solutions (78) are replaced by

()

In (83), both p₀,

are also unknown variables, and the total number of unknowns is now M + N + 2. Then m = n = M + N + 2 in (81).

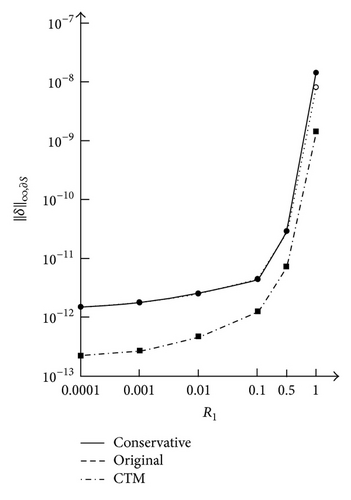
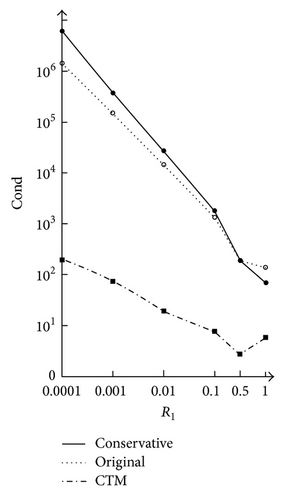
Consider the model problem with R = 2.5 and R₁ = 1 and then shrink the interior hole by decreasing radius R₁ from 1 down to 10⁻⁴. This reflects that Laplace′s equation may occur in an actually punctured disk, where there may be a very small hole but not as a solitary point. For the conservative schemes of the IFM, the errors, condition numbers, and the leading coefficients are listed in Tables 1 and 2, where δ = u − u_M−N. For R₁ = 0.1,0.01,0.001,0.0001, the optimal results are marked in bold. We also note that when R₁ decreases, the errors decrease and the condition numbers increase. Table 2 lists the leading coefficients, p₀, p₁, and . All tables are computed by MATLAB with double precision.

Table 1. The errors and condition numbers by the conservative schemes of the IFM, where R = 2.5 and δ = u − u_M−N.

R₁	(M, N)	∥δ∥_∞,∂S	∥δ∥_0,∂S	Cond	Cond_eff
1	(24, 12)	1.52 (−8)	1.54 (−8)	8.48 (1)	2.70 (1)

0.5	(24, 12)	4.90 (−11)	4.70 (−11)	2.64 (2)	1.30 (2)

0.1	(24, 8)	6.81 (−12)	6.67 (−12)	1.62 (3)	9.21 (2)
0.1	(24, 7)	6.81 (−12)	6.67 (−12)	1.39 (3)	7.89 (2)
0.1	(24, 6)	6.81 (−12)	6.83 (−12)	1.16 (3)	6.58 (2)
0.1	(24, 5)	2.40 (−10)	9.34 (−11)	9.34 (2)	5.26 (2)
0.1	(24, 4)	1.58 (−8)	6.10 (−9)	7.05 (2)	3.95 (2)

10⁻²	(24, 6)	3.69 (−12)	3.62 (−12)	1.97 (4)	1.16 (4)
10⁻²	(24, 5)	6.69 (−12)	3.62 (−12)	1.57 (4)	9.26 (3)
10⁻²	(24, 4)	3.69 (−12)	3.62 (−12)	1.18 (4)	6.94 (3)
10⁻²	(24, 3)	6.10 (−10)	7.63 (−11)	7.91 (3)	4.63 (3)
10⁻²	(24, 2)	4.80 (−7)	6.00 (−8)	3.98 (3)	2.31 (3)

10⁻³	(24, 5)	2.58 (−12)	2.53 (−12)	2.22 (5)	1.32 (5)
10⁻³	(24, 4)	2.58 (−12)	2.53 (−12)	1.67 (5)	9.93 (4)
10⁻³	(24, 3)	2.58 (−12)	2.53 (−12)	1.11 (5)	6.62 (4)
10⁻³	(24, 2)	3.35 (−9)	1.33 (−10)	5.58 (4)	3.31 (4)
10⁻³	(24, 1)	3.52 (−5)	1.39 (−6)	1.09 (2)	7.90 (1)

10⁻⁴	(24, 5)	1.98 (−12)	1.94 (−12)	2.87 (6)	1.72 (6)
10⁻⁴	(24, 4)	1.98 (−12)	1.94 (−12)	2.15 (6)	1.29 (6)
10⁻⁴	(24, 3)	1.98 (−12)	1.95 (−12)	1.44 (6)	8.62 (5)
10⁻⁴	(24, 2)	2.57 (−11)	1.97 (−12)	7.20 (5)	4.31 (5)
10⁻⁴	(24, 1)	2.70 (−6)	3.38 (−8)	1.40 (2)	1.03 (2)

Table 2. The leading coefficients by the conservative schemes of the IFM, where R = 2.5.

R₁	(M, N)	p₀	p₁
1	(24, 12)	5.770780163555825 (−1)	−5.770780163555787 (−1)	7.213475204444549 (−1)

0.5	(24, 12)	2.806196474263354 (−1)	−2.358350543983467 (−1)	2.834834114319612 (−1)

0.1	(24, 8)	1.313991926276972 (−1)	−1.053200366713576 (−1)	1.254266057498590 (−1)
0.1	(24, 7)	1.313991926276972 (−1)	−1.053200366713574 (−1)	1.254266057498546 (−1)
0.1	(24, 6)	1.313991926276971 (−1)	−1.053200366713574 (−1)	1.254266057498543 (−1)
0.1	(24, 5)	1.313991926276971 (−1)	−1.053200366713575 (−1)	1.254266057498583 (−1)
0.1	(24, 4)	1.313991926276965 (−1)	−1.053200366713555 (−1)	1.254266057489581 (−1)

10⁻²	(24, 6)	7.480685008050482 (−2)	−5.984662000415889 (−2)	7.124623469104319 (−2)
10⁻²	(24, 5)	7.480685008050478 (−2)	−5.984662000415886 (−2)	7.124623469102030 (−2)
10⁻²	(24, 4)	7.480685008050478 (−2)	−5.984662000415891 (−2)	7.124623469102347 (−2)
10⁻²	(24, 3)	7.480685008050478 (−2)	−5.984662000415888 (−2)	7.124623469085235 (−2)
10⁻²	(24, 2)	7.480685008030524 (−2)	−5.984662000262044 (−2)	7.124614851570256 (−2)

10⁻³	(24, 5)	5.228968294193471 (−2)	−4.183175432150129 (−2)	4.979970933244982 (−2)
10⁻³	(24, 4)	5.228968294193472 (−2)	−4.183175432150129 (−2)	4.979970933242725 (−2)
10⁻³	(24, 3)	5.228968294193472 (−2)	−4.183175432150130 (−2)	4.979970933271582 (−2)
10⁻³	(24, 2)	5.228968294193472 (−2)	−4.183175432150118 (−2)	4.979970873003448 (−2)
10⁻³	(24, 1)	5.228968256993316 (−2)	−4.183174605594654 (−2)

10⁻⁴	(24, 5)	4.019180446935835 (−2)	−3.215344363673135 (−2)	3.827790910656165 (−2)
10⁻⁴	(24, 4)	4.019180446935836 (−2)	−3.215344363673130 (−2)	3.827790910851808 (−2)
10⁻⁴	(24, 3)	4.019180446935834 (−2)	−3.215344363673132 (−2)	3.827790910677455 (−2)
10⁻⁴	(24, 2)	4.019180446935835 (−2)	−3.215344363673135 (−2)	3.827790909840129 (−2)
10⁻⁴	(24, 1)	4.019180446716058 (−2)	−3.215344357372844 (−2)

As for the computations by the original IFM, the errors, condition numbers, and the leading coefficients are listed in Tables 3 and 4, where only the optimal results are listed. Comparing Table 3 with Table 1, the differences in terms of errors and condition number are insignificant, but the effective condition numbers are much smaller by the original IFM. Strictly speaking, the conservative schemes satisfy the flux conservative law exactly, but the original IFM does not.

Table 3. The errors and condition numbers by the original IFM, where R = 2.5 and δ = u − u_M−N.

R₁	(M, N)	∥δ∥_∞,∂S	∥δ∥_0,∂S	Cond	Cond_eff
1	(24, 12)	8.94 (−9)	8.87 (−9)	1.38 (2)	1.85 (1)
0.5	(24, 12)	4.90 (−11)	4.70 (−11)	2.67 (2)	4.61 (1)
0.1	(24, 6)	6.81 (−12)	6.67 (−12)	8.32 (2)	5.19 (1)
10⁻²	(24, 3)	3.69 (−12)	3.63 (−12)	5.20 (3)	4.54 (1)
10⁻⁴	(24, 2)	1.98 (−12)	1.94 (−12)	3.88 (5)	5.57 (1)

Table 4. The leading coefficients by the original IFM, where R = 2.5.

R₁	(M, N)	p₀	p₁
1	(24, 12)	5.770780163555844 (−1)	−5.770780163555829 (−1)	−1.442695040888961 (0)	7.213475204444735 (−1)
0.5	(24, 12)	2.806196474263354 (−1)	−2.358350543983468 (−1)	−1.403098237131676 (0)	2.834834114319622 (−1)
0.1	(24, 6)	1.313991926276971 (−1)	−1.053200366713573 (−1)	−3.284979815692429 (0)	1.254266057498605 (−1)
10⁻²	(24, 3)	7.480685008050476 (−2)	−5.984662000415886 (−2)	−1.870171252012620 (1)	7.124623469101694 (−2)
10⁻⁴	(24, 2)	4.019180446935834 (−2)	−3.215344363673133 (−2)	−1.004795111733959 (3)	3.827790910389037 (−2)

5.2. The CTM and the BIE

By means of symmetry, we choose the simple particular solutions in the CTM

()

where a_i and

are the true coefficients and (ρ, θ) and

are the polar coordinates with the origins (0,0) and (−1,0), respectively. We have also carried out the computation by CTM and BIE and have given their results in Tables 5, 6, 7, and 8. Comparing Table 7 of the BIE with Table 3 of the original IFM, the errors and the condition numbers are the same, but the effective condition numbers are slightly different. Then we conclude that the performance of the original IFM and BIE is the same. For comparisons of different methods, we draw their curves of errors and condition numbers in Figures 2 and 3, and it is clear that CTM is the best.

Table 5. The errors and condition numbers by the simple particular solutions of the CTM, where R = 2.5 and δ = u − u_M−N.

R₁	(M, N)	∥δ∥_∞,∂S	∥δ∥_0,∂S	Cond	Cond_eff
1	(24, 12)	1.58 (−9)	1.57 (−9)	7.62	3.03
0.5	(24, 12)	8.68 (−12)	8.32 (−12)	4.59	3.93
0.1	(24, 5)	1.21 (−12)	1.19 (−12)	1.31 (1)	1.21 (1)
10⁻²	(24, 3)	6.54 (−13)	6.41 (−13)	5.17 (1)	4.39 (1)
10⁻³	(24, 2)	4.57 (−13)	4.48 (−13)	1.93 (2)	1.57 (2)
10⁻⁴	(24, 1)	3.51 (−13)	3.44 (−13)	6.44 (2)	5.11 (2)

Table 6. The leading coefficients by the CTM, where R = 2.5.

R₁	(M, N)	a₀	a₁
1	(24, 12)	−3.219280948873607 (−1)	−7.213475204444795 (−1)	1.442695040888962 (0)	3.606737602222373 (−1)
0.5	(24, 12)	3.571770447036389 (−1)	−2.947938179979336 (−1)	7.015491185658381 (−1)	7.087085285799036 (−2)
0.1	(24, 5)	6.990003440487363 (−1)	−1.316500458391969 (−1)	3.284979815692430 (−1)	6.271330287492891 (−3)
10⁻²	(24, 3)	8.286379414763349 (−1)	−7.480827500519865 (−2)	1.870171252012619 (−1)	3.562311734550295 (−4)
10⁻³	(24, 2)	8.802186203691674 (−1)	−5.228969290187686 (−2)	1.307242073548369 (−1)	2.489985466613060 (−5)
10⁻⁴	(24, 1)	9.079315551685712 (−1)	−4.019180454591526 (−2)	1.004795111733959 (−1)	1.913895455111127 (−6)

Table 7. The errors and condition numbers by the BIE, where R = 2.5 and δ = u − u_M−N.

R₁	(M, N)	∥δ∥_∞,∂S	∥δ∥_0,∂S	Cond	Cond_eff
1	(24, 12)	8.94 (−9)	8.87 (−9)	1.38 (2)	2.66 (1)

0.5	(24, 12)	4.90 (−11)	4.70 (−11)	2.67 (2)	6.41 (1)
0.1	(24, 5)	7.27 (−12)	7.00 (−12)	7.36 (2)	8.71 (1)
10⁻²	(24, 3)	3.69 (−12)	3.63 (−12)	5.20 (3)	1.12 (2)
10⁻³	(24, 2)	2.58 (−12)	2.53 (−12)	3.88 (4)	1.22 (2)
10⁻⁴	(24, 2)	1.98 (−12)	1.94 (−12)	3.88 (5)	1.59 (2)

Table 8. The leading coefficients by the BIE, where R = 2.5.

R₁	(M, N)
1	(24, 12)	1.405353491806680 (−1)	−5.770780163555832 (−1)	−1.442695040888961 (0)	7.213475204444746 (−1)
0.5	(24, 12)	−1.559230197485811 (−1)	−2.358350543983469 (−1)	−1.403098237131677 (0)	2.834834114319625 (−1)
0.1	(24, 5)	−3.051434745472195 (−1)	−1.053200366713573 (−1)	−3.284979815692429 (0)	1.254266057498587 (−1)
10⁻²	(24, 3)	−3.617358170944118 (−1)	−5.984662000415891 (−2)	−1.870171252012620 (1)	7.124623469100554 (−2)
10⁻³	(24, 2)	−3.842529842329820 (−1)	−4.183175432150123 (−2)	−1.307242073548368 (2)	4.979970933294560 (−2)
10⁻⁴	(24, 2)	−3.963508627055583 (−1)	−3.215344363673110 (−2)	−1.004795111733959 (3)	3.827790910431746 (−2)

6. Concluding Remarks

To close this paper, let us make a few concluding remarks.

(1) By following [17] for the NFM, we propose the interior field method (IFM). Since all boundary methods can be applied to any annular domains, they may be used for circular domains with circular holes; in this paper, we employ the first kind boundary integral equation (BIE) in [30] and the collocation Trefftz method (CTM) in [6]. The relations of expansion coefficients among NFM, IFM, BIE, and CTM are found. The intrinsic relations among them are discovered, to show that the IFM and the BIE are special cases of CTM. Section 2 yields an in-depth overview of four methods for circular domains with circular holes.

(2) For the NFM, some stability analysis in [17] was made for concentric circular boundaries. The error analysis of the NFM is challenging. Sections 3 and 4 are devoted to the error analysis of the NFM. In Section 3, a preliminary analysis is provided. In Section 4, for the special NFM with , the error bounds are provided without proof. The optimal convergence rates can be achieved. The error analysis is important and valid in wide applications, because the special NFM offers the best numerical performance in convergence and stability; see [17].

(3) Numerical experiments are carried out for a challenging problem of the actually punctured disks. We choose NFM, IFM, CTM, and BIE and their conservative schemes. Numerical results are reported from R₁ = 1 down to R₁ = 10⁻⁴. Note that the popular methods, such as the finite element method (FEM), the finite difference method (FDM), and the boundary element method (BEM), may fail to handle this problem. The actually punctured disks may be regarded as a kind of singularity problems, and the local mesh refinements and other innovations of FEM, FDM, and BEM are indispensable. However, their algorithms are complicated and troublesome; see [5]. Consequently, the computation of this paper enriches the boundary methods [6].

(4) Numerical comparisons of different methods are imperative in real application. Though their numerical performances are basically the same, the CTM is best in accuracy, stability, and simplicity of algorithms. Moreover, the CTM can always circumvent the degenerate scale problems encountered in NFM, IFM, and BIE. More importantly, the CTM can be applied to any shape domains and singularity problems (see [5, 6]). In summary, three goals motivated have been fulfilled.

Acknowledgments

The authors are grateful to T. Wriedt and J. T. Chen for their valuable comments and suggestions and indebted to I. S. Lin for the computation in this paper.

References

1 Barone M. R. and Caulk D. A., Special boundary integral equations for approximate solution of Laplace′s equation in two-dimensional regions with circular holes, The Quarterly Journal of Mechanics and Applied Mathematics. (1981) 34, no. 3, 265–286, https://doi.org/10.1093/qjmam/34.3.265, MR627272.
10.1093/qjmam/34.3.265
Web of Science® Google Scholar
2 Barone M. R. and Caulk D. A., Special boundary integral equations for approximate solution of potential problems in three-dimensional regions with slender cavities of circular cross-section, IMA Journal of Applied Mathematics. (1985) 35, no. 3, 311–325, https://doi.org/10.1093/imamat/35.3.311, MR841909.
10.1093/imamat/35.3.311
Web of Science® Google Scholar
3 Caulk D. A., Analysis of steady heat conduction in regions with circular holes by a special boundary-integral method, IMA Journal of Applied Mathematics. (1983) 30, 231–246.
10.1093/imamat/30.3.231
Web of Science® Google Scholar
4 Bird M. D. and Steele C. R., A solution procedure for Laplace’s equation on multiply connected circular domains, Journal of Applied Mechanics. (1992) 59, 398–3404.
10.1115/1.2899533
Web of Science® Google Scholar
5 Li Z. C., Combined Methods for Elliptic Equations with Singularities, Interfaces and Infinities, 1998, Kluwer Academic Publishers, Boston, Mass, USA, https://doi.org/10.1007/978-1-4613-3338-8, MR1639538.
10.1007/978-1-4613-3338-8
Google Scholar
6 Li Z.-C., Lu T.-T., Hu H.-Y., and Cheng A. H.-D., Trefftz and Collocation Methods, 2008, WIT Press, Boston, Mass, USA, MR2408330.
Google Scholar
7 Ang W. T. and Kang I., A complex variable boundary element method for elliptic partial differential equations in a multiple-connected region, International Journal of Computer Mathematics. (2000) 75, no. 4, 515–525, https://doi.org/10.1080/00207160008805001, MR1806532.
10.1080/00207160008805001
Web of Science® Google Scholar
8 Chen J. T., Kuo S. R., and Lin J. H., Analytical study and numerical experiments for degenerate scale problems in the boundary element method for two-dimensional elasticity, International Journal for Numerical Methods in Engineering. (2002) 54, no. 12, 1669–1681.
10.1002/nme.476
Web of Science® Google Scholar
9 Chen J. T., Lee C. F., Chen J. L., and Lin J. H., An alternative method for degenerate scale problem in boundary element methods for two-dimensional Laplace equation, Engineering Analysis with Boundary Elements. (2002) 26, 559–569.
10.1016/S0955-7997(02)00024-3
Web of Science® Google Scholar
10 Chen J.-T. and Shen W.-C., Degenerate scale for multiply connected Laplace problems, Mechanics Research Communications. (2007) 34, no. 1, 69–77, https://doi.org/10.1016/j.mechrescom.2006.06.009, MR2264456.
10.1016/j.mechrescom.2006.06.009
Web of Science® Google Scholar
11 Chen J.-T. and Shen W.-C., Null-field approach for Laplace problems with circular boundaries using degenerate kernels, Numerical Methods for Partial Differential Equations. (2009) 25, no. 1, 63–86, https://doi.org/10.1002/num.20332, MR2473680.
10.1002/num.20332
CAS Web of Science® Google Scholar
12 Chen J. T., Shieh H. C., Lee Y. T., and Lee J. W., Bipolar coordinates, image method and the method of fundamental solutions for Green′s functions of Laplace problems containing circular boundaries, Engineering Analysis with Boundary Elements. (2011) 35, no. 2, 236–243, https://doi.org/10.1016/j.enganabound.2010.08.008, MR2740348.
10.1016/j.enganabound.2010.08.008
Web of Science® Google Scholar
13 Chen J. T., Wu C. S., and Chen K. H., A study of free terms for plate problems in the dual boundary integral equations, Engineering Analysis with Boundary Elements. (2005) 29, 435–446.
10.1016/j.enganabound.2004.12.006
Web of Science® Google Scholar
14 Kuo S. R., Chen J. T., and Kao S. K., Linkage between the unit logarithmic capacity in the theory of complex variables and the degenerate scale in the BEM/BIEMs, Applied Mathematics Letters. (2013) 29, 929–938.
10.1016/j.aml.2013.04.011
Google Scholar
15 Lee M.-G., Li Z.-C., Huang H.-T., and Chiang J. Y., Conservative schemes and degenerate scale problems in the null-field method for Dirichlet problems of Laplace′s equation in circular domains with circular holes, Engineering Analysis with Boundary Elements. (2013) 37, no. 1, 95–106, https://doi.org/10.1016/j.enganabound.2012.08.009, MR2999656.
10.1016/j.enganabound.2012.08.009
CAS Web of Science® Google Scholar
16 Lee M.-G., Li Z.-C., Zhang L. P., Huang H.-T., and Chiang J. Y., Algorithm singularity of the null-field method for Dirichlet problems of Laplace’s equation in annular and circular domains, submitted to. Engineering Analysis with Boundary Elements.
Google Scholar
17 Li Z.-C., Huang H.-T., Liaw C.-P., and Lee M.-G., The null-field method of Dirichlet problems of Laplace′s equation on circular domains with circular holes, Engineering Analysis with Boundary Elements. (2012) 36, no. 3, 477–491, https://doi.org/10.1016/j.enganabound.2011.09.009, MR2868650.
10.1016/j.enganabound.2011.09.009
Web of Science® Google Scholar
18 Kupradze V. D. and Aleksidze M. A., The method of functional equations for the approximate solution of certain boundary-value problems, USSR Computational Mathematics and Mathematical Physics. (1964) 4, 82–126, MR0168171.
10.1016/0041-5553(64)90006-0
Google Scholar
19 Fairweather G. and Karageorghis A., The method of fundamental solutions for elliptic boundary value problems, Advances in Computational Mathematics. (1998) 9, no. 1-2, 69–95, https://doi.org/10.1023/A:1018981221740, MR1662760.
10.1023/A:1018981221740
Web of Science® Google Scholar
20 Chen C. S., Hon Y. C., and Schaback R. A., Scientific computing with radial basis functions [Ph.D. thesis], 2005, Department of Mathematics, University of Southern Mississippi, Hattiesburg, Miss, USA.
Google Scholar
21 Li Z.-C., Huang H.-T., Lee M.-G., and Chiang J. Y., Error analysis of the method of fundamental solutions for linear elastostatics, Journal of Computational and Applied Mathematics. (2013) 251, 133–153, https://doi.org/10.1016/j.cam.2013.03.018, MR3048582.
10.1016/j.cam.2013.03.018
Web of Science® Google Scholar
22 Li Z.-C., Huang J., and Huang H.-T., Stability analysis of method of fundamental solutions for mixed boundary value problems of Laplace′s equation, Computing. (2010) 88, no. 1-2, 1–29, https://doi.org/10.1007/s00607-010-0081-4, MR2645101.
10.1007/s00607-010-0081-4
Web of Science® Google Scholar
23 Wriedt T., Review of the null-field method with discrete source, Journal of Quantitative Spectroscopy and Radiative Transfer. (2007) 106, 534–545.
10.1016/j.jqsrt.2007.01.043
Web of Science® Google Scholar
24 Doicu A. and Wried T., Calculation of the T matrix in the null-field method with discret sources, The Journal of the Optical Society of America. (1999) 16, 2539–2544.
10.1364/JOSAA.16.002539
Web of Science® Google Scholar
25 Hellmers J., Schmidt V., and Wriedt T., Improving the numerical instability of T-matrix light scattering calculations for extreme articles shapes using the nullfield method with discrete sources, Journal of Quantitative Spectroscopy and Radiative Transfer. (2011) 112, 1679–1686.
10.1016/j.jqsrt.2011.02.004
CAS Web of Science® Google Scholar
26 Palaniappan D., Electrostatics of two intersecting conducting cylinders, Mathematical and Computer Modelling. (2002) 36, no. 7-8, 821–830, https://doi.org/10.1016/S0895-7177(02)00229-7, MR1950735.
10.1016/S0895-7177(02)00229-7
Web of Science® Google Scholar
27 Abramowitz M. and Stegun I. A., Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, 1964, Dover Publications, New York, NY, USA.
Web of Science® Google Scholar
28 Atkinson K. E., A Survey of Numerical Methods for the Solutions of Fredholm Integral Equations of the Second Kind, 1997, Cambridge University Press.
10.1017/CBO9780511626340
Google Scholar
29 Hsiao G. C. and Wendland W. L., Boundary Integral Equations, 2008, Springer, Berlin, Germany, https://doi.org/10.1007/978-3-540-68545-6, MR2441884.
10.1007/978-3-540-68545-6
Web of Science® Google Scholar
30 Liem C. B., Lü T., and Shih T. M., The Splitting Extrapolation Method, 1995, World Scientific, Singapore, MR1372266.
10.1142/2708
Google Scholar
31 Kreiss H.-O. and Oliger J., Stability of the Fourier method, SIAM Journal on Numerical Analysis. (1979) 16, no. 3, 421–433, https://doi.org/10.1137/0716035, MR530479.
10.1137/0716035
Web of Science® Google Scholar
32 Pasciak J. E., Spectral and pseudospectral methods for advection equations, Mathematics of Computation. (1980) 35, no. 152, 1081–1092, https://doi.org/10.2307/2006376, MR583488.
10.2307/2006376
Web of Science® Google Scholar
33 Canuto C. and Quarteroni A., Approximation results for orthogonal polynomials in Sobolev spaces, Mathematics of Computation. (1982) 38, no. 157, 67–86, https://doi.org/10.2307/2007465, MR637287.
10.1090/S0025-5718-1982-0637287-3
Web of Science® Google Scholar
34 Canuto C., Hussaini M. Y., Quarteroni A., and Zang T. A., Spectral Methods, Fundamentals in Single Domains, 2006, Springer, New York, NY, USA, MR2223552.
10.1007/978-3-540-30726-6
Google Scholar
35 Li Z.-C., Huang H.-T., Wei Y., and Cheng A. H.-D., Effective Condition Number for Numerical Partial Differential Equations, 2013, Science Press, Beijing, China.
Google Scholar

All articles

Null Field and Interior Field Methods for Laplace’s Equation in Actually Punctured Disks

Abstract

1. Introduction

2. The Null Field Method and Other Algorithms

2.1. The Null Field Method

2.2. Conservative Schemes

2.3. The Interior Field Method

2.4. The First Kind Boundary Integral Equations

2.5. The Collocation Trefftz Method

3. Preliminary Analysis of the NFM

4. Error Bounds of the NFM with

5. Numerical Experiments

5.1. IFM and Its Conservative Schemes

5.2. The CTM and the BIE

6. Concluding Remarks

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Null Field and Interior Field Methods for Laplace’s Equation in Actually Punctured Disks

Abstract

1. Introduction

2. The Null Field Method and Other Algorithms

2.1. The Null Field Method

2.2. Conservative Schemes

2.3. The Interior Field Method

2.4. The First Kind Boundary Integral Equations

2.5. The Collocation Trefftz Method

3. Preliminary Analysis of the NFM

4. Error Bounds of the NFM with

5. Numerical Experiments

5.1. IFM and Its Conservative Schemes

5.2. The CTM and the BIE

6. Concluding Remarks

Acknowledgments

References

Figures

References

Related

Information