Nonlinear Dynamic Analysis on the Rain-Wind-Induced Vibration of Cable Considering the Equilibrium Position of Rivulet

1. Introduction

Dynamic behavior of corresponding differential systems has been of extensive concern and investigated by many scholars [1–8]. One of the systems is the inclined cable, which is a structure characterized by small stiffness, low mass, and light damping. The similar structures including transmission line, suspended cable, and submarine cable are widely used in the long-span structures, so the dynamic study of the inclined cable is of great engineering significance. Rain-wind-induced vibration of inclined cable is a phenomenon of large amplitude vibration with low frequency under the conditions of rain and wind. Many wind tunnel tests have been carried on a cable model. Large amplitude vibrations of cables were first observed by Hikami and Shiraishi [9]. Upper rivulet was regarded as the origin of large amplitude vibration due to its formulation on the cable, causing the cable cross section aerodynamically unstable. Yamaguchi [10] took the lead in aerodynamic test of cable with artificial rivulet. Aerodynamic forces acting on the cable were obtained. Matsumoto et al. [11] reported that another factor named an axial flow generated at the near wake of the inclined cable may trigger the rain-wind-induced oscillations. He stated that rain-wind-induced vibration can be explained as a vortex-induced vibration, which occurs at limited high reduced wind velocity region [12]. Bosdogianni and Olivari [13] compared wind tunnel results of cables with moving rivulet and fixed rivulet. They concluded that it was the presence of rivulet at certain positions on the surface of cable and not the motion of rivulet that caused cable instability. Then the aerodynamic forces acting on the moving rivulet were first measured by Gu et al. [14], proposing a new description of friction force between the water rivulet and the cable surface.

On the basis of the measured aerodynamic coefficients, the kinetic equations of rain-wind-induced vibration have been established. However, before the measurement of the aerodynamic coefficients on the moving rivulet, the motion of rivulet was assumed to be harmonic [15–17]. With the acquisition of the aerodynamic coefficients on the moving rivulet, the analytic model for cable with the kinetic equation of the rivulet was built [18]. Zhang et al. [3] presented a two-degree-of-freedom model of the rain-wind-induced vibration of a continuous stay cable. The phenomenon of bifurcation was observed in the system using the singularity theory. Zhang et al. [19] established the three-degree-of-freedom model of rain-wind-induced vibration of inclined cable. The motion characteristics of rivulet were achieved with two rivulet models through numerical calculation and some more rational explanations of the phenomenon were obtained.

The influences of equilibrium position of rivulet on cable have been studied, in which the equilibrium position of rivulet was always assumed to be independent of wind. The equilibrium position of rivulet was altered factitiously to inspect its effects on the vibration while the mean wind velocity was fixed [15, 18]. However, the equilibrium position of rivulet is uniquely corresponding to the wind once the mass of the rivulet is fixed. Meanwhile, the similar structures including beam, suspended cables, and inclined cable without wind or rain have been extensively researched analytically to discover more dynamic phenomena [4–8]. However, the nonlinear dynamic behavior of rain-wind-induced vibration has been rarely investigated using approximately analytic method for its complexity.

In comparison with the literature above, the equilibrium position of the moving rivulet is considered and the nonlinear dynamic characteristics of rain-wind-induced vibration are investigated analytically by using the approximate method of averaging. The present paper established the continuum model of the inclined cable subjected to wind and rain turbulence with the consideration of the equilibrium position of the rivulet. The reliance of the equilibrium position of the rivulet on wind is figured out and the effects of the equilibrium position of the rivulet on the cable vibration are observed and proved. Furthermore, the amplitude response curves of parameters including mean wind velocity, Coulomb damping force, damping ratio, the span length, and the initial tension of the inclined cable present abundant dynamic behaviors. The jump phenomenon is also observed when multivalued solutions exit in the system.

2. Model and Nonlinear Equations

Assumptions of inclined cable are made in present paper: (1) The flexural rigidity, torsional stiffness and shear stiffness are ignored; (2) The constitutive relation of cable deformation submits to Hooke′s law and the points bear the stress evenly; (3) The axial motion of the cable is ignored; (4) The influences of bridge and tower are disregarded.

The analytic model of rain-wind-induced vibration of inclined cable is shown in Figures 1(a), 1(b), and 1(c), U₀ is mean wind velocity, α is cable angle, β is wind angle, L is the span length of the cable, and v and w are dynamic displacement in the y and z direction, respectively. v₀ is deflection at the equilibrium position of cable. Define that the vibration in the plane x-y is in-plane vibration, while the vibration in the plane x-y is out-of-plane vibration. M is the mass per unit length of cable, T is the initial tension of the cable, and τ is the dynamic tension of the cable. ds and ds₀ are arc length of undeformed and deformed cable, respectively.

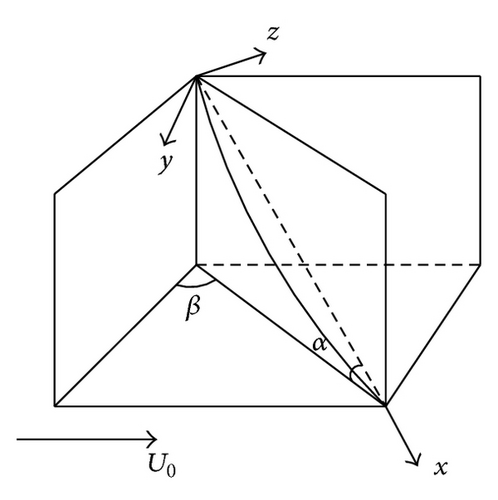
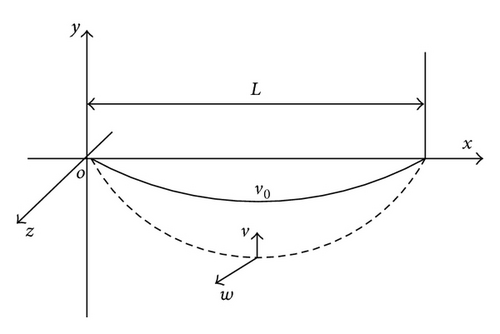
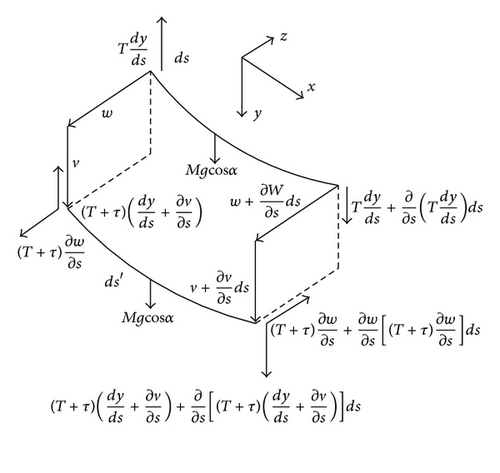
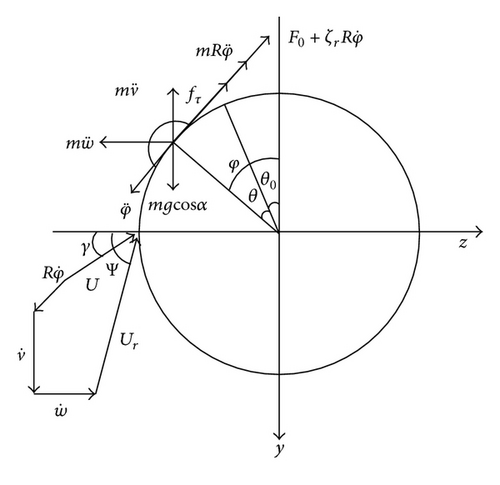
Figure 1(d) presents the force analysis of rivulet. θ₀ is the equilibrium position of rivulet, θ is dynamic displacement of rivulet which is the angle deviating from the equilibrium position, φ is dynamic displacement of rivulet which is the angle deviating from y direction. m is the mass per unit length of rivulet, g is the gravity acceleration, R is the radius of cable, F₀ is Coulomb damping force whose direction is opposite to its motion, ζ_r is the linear viscous damping coefficient between cable and rivulet, and effective angle of attack γ is the angle between effective wind velocity U and z direction. ψ is the angle between relative wind velocity U_r and z direction.

3. Average Analysis

4. Results Analysis

Parameters are selected as follows [20]: M = 64.8 kg/m, L = 110.5 m, R = 0.051275 m, T = 4.9 × 10⁶ N, A = 8.26 × 10⁻³ m², E = 2.10 × 10¹¹ Pa, α = 30^°, β = 35^°, ζ₁ = 0.1%, ζ₂ = 0.1%, ζ_r = 0.0008 Ns/m², U₀ = 8 m/s, m = 0.16 kg/m, and F₀ is 10% of rivulet’s mass per unit length.

4.1. Numerical Solutions

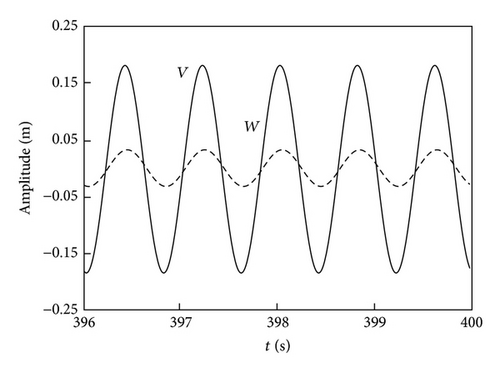
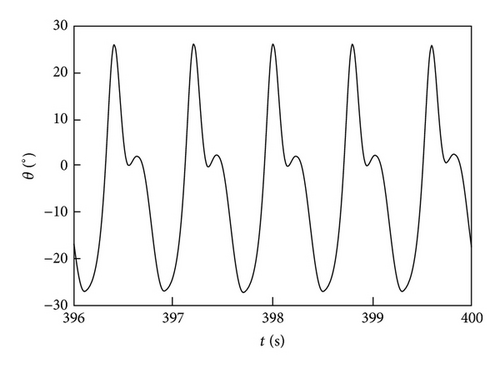
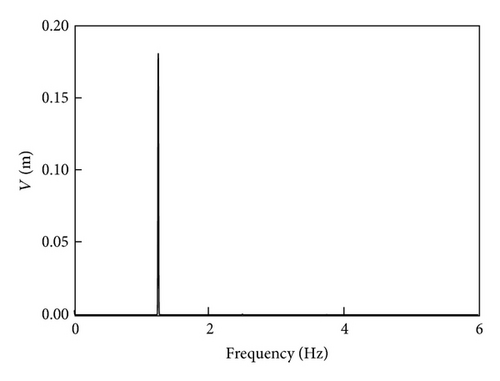
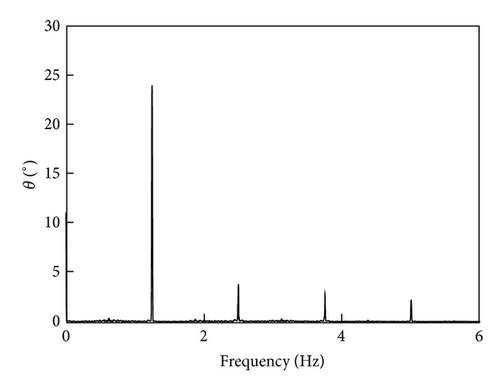
Figure 2 shows the numerical solutions of inclined cable vibration calculated form system (8) utilizing Matlab. The full line in Figure 2(a) is the time-history of in-plane vibration while the dotted line represents the out-of-plane vibration of the cable. The in-plane amplitude is about 4 times as that of out-of-plane vibration and they have the same phase. The time-history of the displacement response of the rivulet is presented in Figure 2(b). The moving rivulet vibrates at its equilibrium position. Note that, the vibration is not exhibited to be harmonic and there is not one frequency component. Figure 3 provides the vibration frequencies of in-plane and rivulet vibration. Cable vibrates at its natural frequency which is equal to 1.25 Hz as shown in the Figure 3(a). However, the frequency components of rivulet vibration are more complex. As shown in Figure 3(b), its primary frequency is the same as the natural frequency of cable; in addition, some higher order frequencies also exist in its vibration.

4.2. The Comparison between Analytic and Numerical Solutions

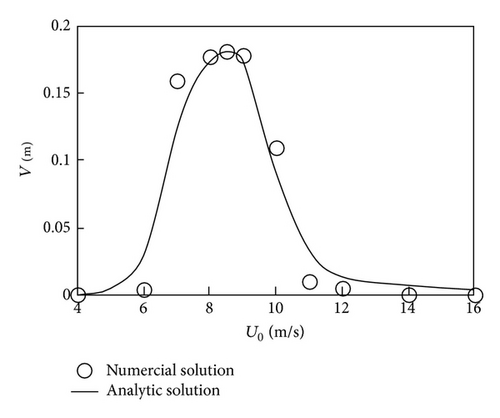
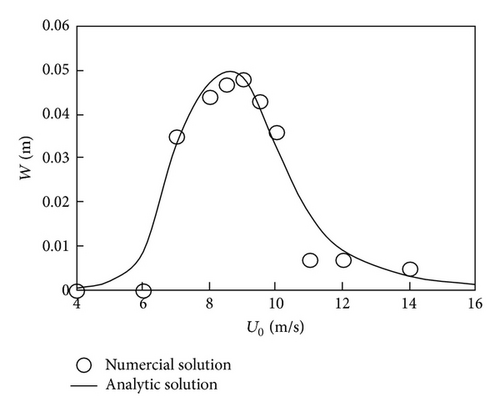
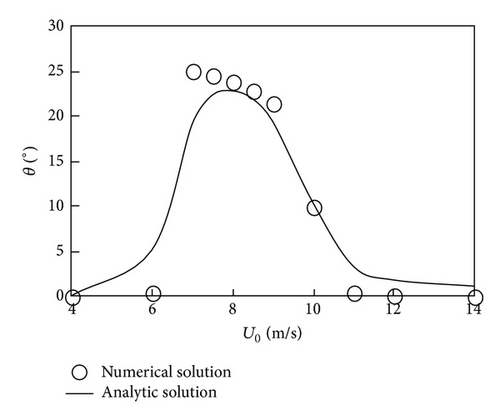
Figure 4 represents the analytic solutions together with the numerical results. The x-coordinate is the mean wind velocity U₀ and the y-coordinate is the maximum displacement response amplitude of the in-plane, out-of-plane, and rivulet vibration, respectively. Analytic solution is a smooth curve, describing the trend of the amplitude more directly and visually. Numerical solutions are several discrete points. The amplitudes of in-plane, out-of-plane, and rivulet vibration present a directly proportional relationship. The response curves also confirm that rain-wind-induced inclined cable vibration is a kind of restricted amplitude vibration rather than galloping. The analytic results are in good agreement with the numerical results. Thus, the validity of the approximately analytic method is proved.

4.3. Analysis of Equilibrium Position of Rivulet

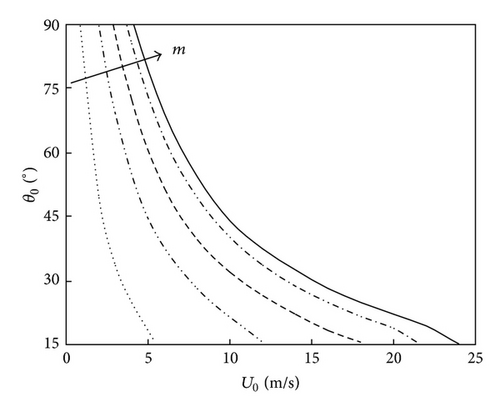
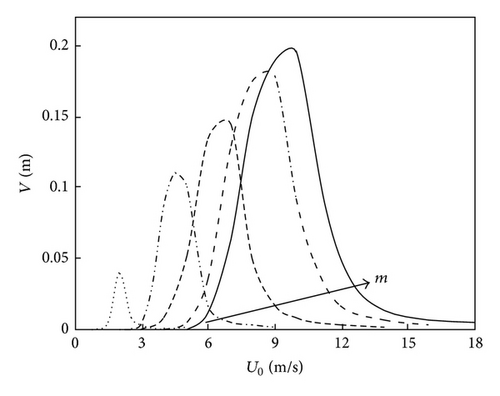
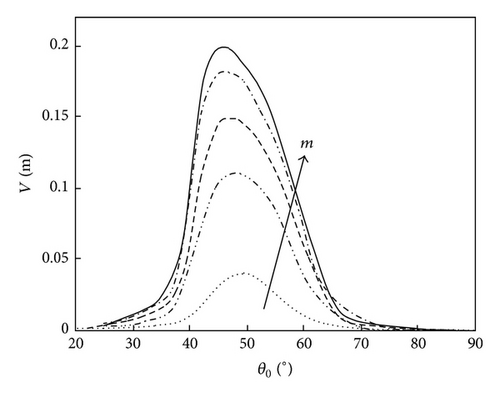
The correspondences among the equilibrium position of rivulet, mean wind velocity, and rivulet mass are calculated from (6) and shown in Figure 5(a). The equilibrium position of rivulet is determined by mean wind velocity with certain rivulet mass. The effective wind velocity is around 1 m/s~24 m/s. Greater rivulet mass needs larger mean wind velocity to form on the surface of the inclined cable. Keeping the other parameters invariant, the effects of rivulet mass on the cable vibration subjected to variational mean wind velocity are presented in Figure 5(b). Greater rivulet mass on the surface of inclined cable will cause stronger oscillation. The impact of the equilibrium position of rivulet on the inclined cable is investigated and plotted in Figure 5(c). It can be perceived that the amplitude is up to the maximum when the equilibrium position of rivulet is around 48° and almost irrelevant to the rivulet mass. It confirms that the presence of rivulet at certain positions on the surface of inclined cable is one of the trigger that stimulate the inclined cable to vibrate.

4.4. Nonlinear Dynamic Analysis

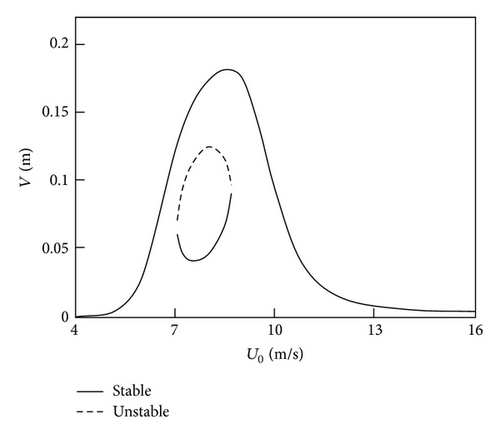
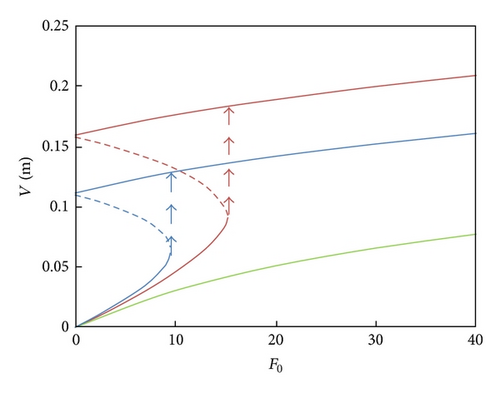
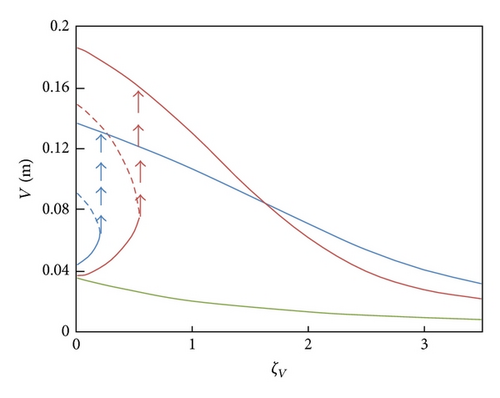
The nonlinear dynamic behavior of cable reflected by parameters is given in Figure 6. The effect of mean wind velocity on the cable is presented in Figure 6(a), in which the full line is stable solution and the dotted line represents unstable solution. The figure illustrates that the mean wind velocity modify the number of the solutions. Two stable solutions appear at the mean wind velocity range from 7 m/s to 8.7 m/s. Figure 6(b) describes the nonlinear response curve of Coulomb damping force F₀ acting on the cable amplitude subjected to various mean wind velocities. When mean wind velocity U₀ is selected as 8 m/s, two stable solutions occur for F₀ is less than 15%. As F₀ increases, the amplitude of inclined cable first arises along the smaller branch of the stable solution and it will not jump until F₀ reaches 15%. Once F₀ increases to 15%, the smaller branch of amplitude will be substituted by the larger branch. The jump phenomena will also exist while F₀ is about 9% for U₀ is 7 m/s. The variance of F₀ will make no change to the number of solution while the mean wind velocity is 6 m/s, where the system has only one stable solution and no jump phenomena occurs. Similarly, the response curve of damping ratio acting on the inclined cable depicts the nonlinear behavior of the system (Figure 6(c)). Multiple solutions lie in the certain range of ζ_v when U₀ is beyond its critical mean wind velocity 7 m/s; otherwise, unique solution is obtained irrelevant to the damping ratio.

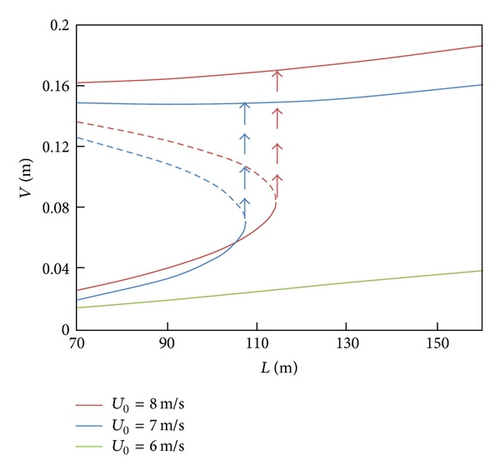
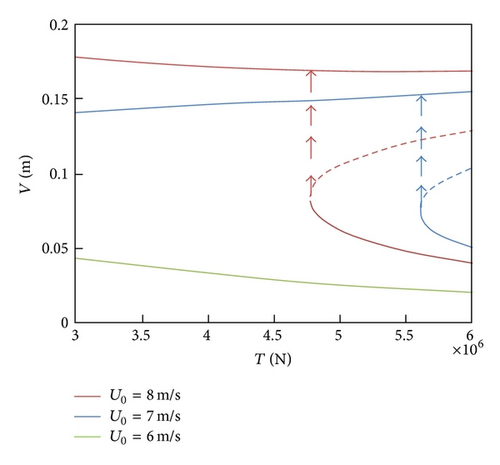
The relation curves of amplitude and the span length of cable L are obtained in Figure 6(d). It also illustrates that the mean wind velocity modified the stability of the inclined cable. When the mean wind velocity is selected as 7 m/s or 8 m/s, the amplitude will jump to a solution of higher branch as the span length of lengthens. However, the mean wind velocity of 6 m/s will not cause the modification of the number of the solutions but only a slight increase. Figure 6(e) shows the response curve of cable amplitude and initial tension T. Similarly, the mean wind velocity of 7 m/s and 8 m/s will cause cable amplitude to increase drastically while the lower wind velocity acting on the cable makes little sense to the variance of the initial tension.

5. Conclusions

The continuum model of inclined cable subjected to wind with moving rivulet on its surface is established considering the equilibrium position of the rivulet. The Galerkin and average methods are adopted to analyze the cable system analytically. The correspondence between mean wind velocity and the equilibrium position of the rivulet is ascertained considered the different rivulet mass. The equilibrium position of the rivulet is proved to be one of the major roles in determining the maximum amplitude of the oscillating cable.

The nonlinear dynamic behavior of the rain-wind-induced cable vibration is then investigated considering the continuous change of parameters including mean wind velocity, Coulomb damping force, damping ratio, the span length, and the initial tension of the inclined cable. Mean wind velocity is observed to be a significant factor in jump phenomena, which is discovered in the range of multiple solutions.