Advances in Tribology
Volume 2013, Issue 1 918387
Research Article
Open Access

Mechanical Hybrid KERS Based on Toroidal Traction Drives: An Example of Smart Tribological Design to Improve Terrestrial Vehicle Performance

Francesco Bottiglione, 

Francesco Bottiglione

Dipartimento di Meccanica, Matematica e Management, Politecnico di Bari, V.le Japigia 182, 70126 Bari, Italy poliba.it

Search for more papers by this author
Giuseppe Carbone, 

Corresponding Author

Giuseppe Carbone

Dipartimento di Meccanica, Matematica e Management, Politecnico di Bari, V.le Japigia 182, 70126 Bari, Italy poliba.it

Search for more papers by this author
Leonardo De Novellis, 

Leonardo De Novellis

University of Surrey, Faculty of Engineering and Physical Sciences, Guildford, Surrey GU2 7XH, UK surrey.ac.uk

Search for more papers by this author
Luigi Mangialardi, 

Luigi Mangialardi

Dipartimento di Meccanica, Matematica e Management, Politecnico di Bari, V.le Japigia 182, 70126 Bari, Italy poliba.it

Search for more papers by this author
Giacomo Mantriota, 

Giacomo Mantriota

Dipartimento di Meccanica, Matematica e Management, Politecnico di Bari, V.le Japigia 182, 70126 Bari, Italy poliba.it

Search for more papers by this author
First published: 25 March 2013
https://doi.org/10.1155/2013/918387
Citations: 12
Academic Editor: Michel Fillon

Abstract

We analyse in terms of efficiency and traction capabilities a recently patented traction drive, referred to as the double roller full-toroidal variator (DFTV). We compare its performance with the single roller full-toroidal variator (SFTV) and the single roller half-toroidal variator (SHTV). Modeling of these variators involves challenging tribological issues; the traction and efficiency performances depend on tribological phenomena occurring at the interface between rollers and disks, where the lubricant undergoes very severe elastohydrodynamic lubrication regimes. Interestingly, the DFTV shows an improvement of the mechanical efficiency over a wide range of transmission ratios and in particular at the unit speed ratio as in such conditions in which the DFTV allows for zero-spin, thus strongly enhancing its traction capabilities. The very high mechanical efficiency and traction performances of the DFTV are exploited to investigate the performance of a flywheel-based Kinetic Energy Recovery System (KERS), where the efficiency of the variator plays an important role in determining the overall energy recovery performance. The energy boost capabilities and the round-trip efficiency are calculated for the three different variators considered in this study. The results suggest that the energy recovery potential of the mechanical KERS can be improved with a proper choice of the variator.

1. Introduction

Recent developments in the automotive field are related to the design of drive-trains with the aim of improving the exploitation of the thermal engine, according to the requirements of reduction of fuel consumption and polluting emissions [1–3].

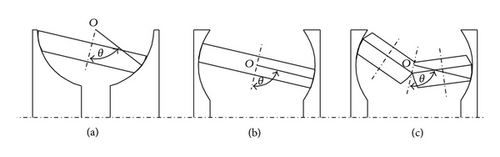
To achieve these targets, hybrid powertrains are being studied and developed. Among all possibilities, some research works claim that mechanical hybrids are more efficient and give the greatest advantages in terms of reduction of fuel consumption and polluting emissions. Several investigations have been made to estimate the effective benefits that such systems can give in mainstream cars and trucks at the present state-of-the-art. Computational results demonstrate that a fuel economy improvement up to 25% can be obtained in mainstream passenger cars and trucks, which can also be improved further with engine downsizing [4–7]. Continuously variable drives are the core of mechanical hybrids. Chain/belt continuously variable transmissions (CVTs) have been widely studied either theoretically either experimentally [8–10]; however, limitations of the maximum transmittable torque and of control possibilities made the toroidal traction variators a valid alternative for the development of CVT drivetrains [11]. A toroidal traction drive is made of input and output disks, which are coupled, respectively, with drive and driven shafts and shaped in such a way to realize a toroidal cavity. A power roller, rotating inside the toroidal cavity, is employed to transfer torque from the drive disk to the driven one, by means of shearing action of elastohydrodynamic oil film; furthermore, the tilting of the power roller allows shifting maneuvers. Referring to the toroidal variators which are actually on the market for automotive applications, the basic geometric distinction is on the position of the roller tilting center (point O in Figure 1), which may coincide or not with the center of the toroidal cavity. In the first case one obtains the so called full-toroidal variator (see Figure 1(b)) in the second case the half-toroidal variator is obtained (see Figure 1(a)). In Figure 1(c), a new patented toroidal geometry [12], the so-called double roller full toroidal variator (or DFTV), is shown; two counter-rotating rollers are arranged inside the full-toroidal cavity, with the aim to reduce the spin losses at the roller-disk contact; also, the roller conical shape allows to balance the normal forces, thus making the employment of a thrust roller-bearing unnecessary. In this way, the main advantages of the two single-roller toroidal geometries (i.e., the SHTV and SFTV) can be combined leading to significant improvements of the overall transmission efficiency [13, 14]. The ratio spread and the efficiency of the variable drives are key features for application to mechanical hybrid systems. A compromise between a large ratio spread and a good efficiency in both forward and reverse operation must be found to optimize the operating conditions of the KERS. It has been shown (see [15]) that shunted CVT architectures ([16, 17]) which enlarge the ratio spread of the variable drive, cannot improve the performance of the KERS as a consequence of a loss of efficiency, in particular in reverse operation (see also [18]). For these reasons, in this paper, we focus on the performance of standard toroidal traction drive geometries with speed ratio covering the range from 0.5. to 2. In particular, a fully flooded elastohydrodynamic-lubrication (EHL) model is presented to analyze, in terms of traction and efficiency performance, a recently patented toroidal traction drive variator (the DFTV) and compare it with more standard solutions as the single roller full-toroidal variator (SFTV) and the single roller half-toroidal variator (SHTV). The results are used to investigate the performance of a flywheel-based Kinetic Energy Recovery System (KERS) where the efficiency of the variator plays an important role in determining the overall energy recovery performance.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
A schematic drawing of the three toroidal variators: the single roller half-toroidal variator (SHTV), (a); the single roller full-toroidal variator (SFTV), (b); the double roller full toroidal variator (c).

2. Traction and Efficiency of Toroidal Drives

In this section, we define the main geometric and kinematic characteristics of the toroidal variators. In Figure 2,  r0 is the first principal radius of the input and output disc, r11 and r33 are the second principal radii, respectively, of the input and output discs. In the case of the DFTV, each power roller has a conical part and a toroidal part; the rollers are in contact along the conical part, whilst the toroidal part is shaped as a typical half-toroidal roller and it is in contact with the input or output disc. We call r2 the curvature radius of a section perpendicular to the roller axis, and r22 is the second principal radius. For practical aspects, it is useful to define the conformity ratio CR = r22/r0 and the aspect ratio k = e/r0, where e is the eccentricity. An important control parameter is the tilting angle γ. We can express the dimensionless disks curvature radii formulation as a function of the cone angle θ and of the tilting angle γ (see Figure 2) as r11 = r1/cos (θ + γ) and r33 = r3/cos (θ − γ), where r1 = r0(1 + k − cos (θ + γ)) and r3 = r0(1 + k − cos (θ − γ)). From geometric relations, we also obtain r2 = (r0 + e)sin(α/2). We also define the geometric speed ratio as the ratio of the radial coordinates r1 and r2; namely, . Said ω1 the input angular velocity and ω3 the rotational speed of the output disc, we define the speed ratio sr as sr = ω3/ω1. Percentage differences of the velocities of the sliding contact pairs are taken into account by defining input and output creep coefficients, respectively, that is, and . The roller-roller slip coefficient is defined as , where ω2 and are the angular velocities of the two counter-rotating rollers. The transmission ratio can be expressed as
(1)
with . For each roller i of the roller pair, we can define the point Θi, which represents the point of intersection of the tangents to the toroidal cavity at the roller-disk contact points, and Ωi is defined as the intersection point of the roller and disk rotation absolute axes. The angular velocities of the roller relative to the input and output disks, ω21 = ω2 − ω1 and have spin velocity components, ω21spin and ω23spin, which can be directed inwards or outwards. By choosing a proper value of the cone incidence angle α, it is possible to have zero spin velocities at . The spin coefficients can be defined as
(2)
Following the same approach proposed in [13, 14], let us define the traction coefficient μ = FT/FN as the ratio between the tangential force at the roller-disk interface FT and the normal load FN and the spin momentum coefficient χ = MS/FNr, where MS is the spin momentum and r the disk radial coordinate of the contact point. From the momentum equation applied to the counter-rotating rollers about each roller axis, the parameters μ and χ have been calculated according to [13, 14]. Consider
(3)
considering that the angle θDT = (π − α)/2 (see Figure 2) and the radial coordinates in dimensionless form, namely, and . The term tB represents the dimensionless torque losses due to roller bearings on the variator roller axes, which have been evaluated according to the SKF technical documentation [19]. From the equilibrium equations of the discs, we can evaluate the effective torque coefficients at the input and output variator side as
(4)
with tin = Tin/(mnFNr1) and tout = Tout/(mnFNr3) can be interpreted as effective torque coefficients at the input and output variator side. In the previous relations, we have considered the possibility to arrange n set of rollers inside m toroidal cavities. Moreover, we can express the thrust force acting in the disk axial direction FD as a function of the normal load FN and of the tilting angle γ:
(5)
The overall mechanical efficiency can be written as
(6)
A fully flooded isothermal contact model [13, 14, 20] has been utilized to calculate the shear stresses at the interface of the elements in contact, and thus, the traction and spin coefficients.
Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
The geometry of the DFTV (a) and of the SHTV (b).
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
The geometry of the DFTV (a) and of the SHTV (b).

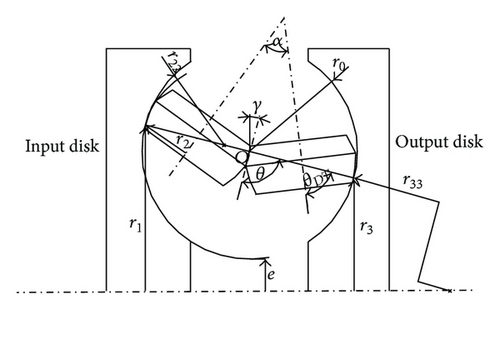
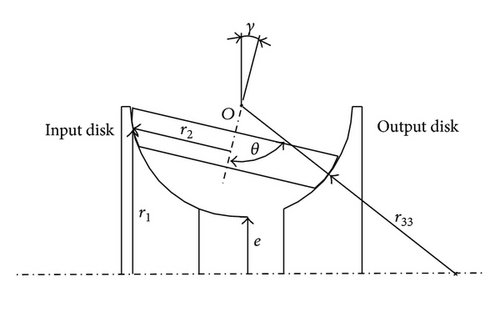
3. The Contact Model

We distinguish the contact conditions at the roller-disk interface, where the contact area is elliptical and at the roller-roller interface, where instead the contact area is rectangularly shaped. To study the contact between two curved profiles a and b, we define an equivalent Young’s modulus E′, expressed as a function of the elasticity modulus E and Poisson’s ratio ν of each element in contact [20]
(7)
and an equivalent curvature radius , with
(8)
(9)
where the subscript a refers to the roller and b to the disk, and , , and (in the case of half- and full-toroidal ). The equivalent radius of curvature is then defined as
(10)
In the case of roller-roller conical contact, we define , being rC the mean rolling radius of the conical part of the rollers, whereas . We can, then, define the equivalent radius of curvature as
(11)
The results of elasto-hydrodynamic theory are employed to describe the lubrication regime on the contact area. In particular, we have considered the viscosity-pressure effect with the Roeland’s formula:
(12)
Because of the very high shear rates, the lubricant shows a nonlinear relation between the shear stresses τij and the shear strain rates , according to the common rule used in the plasticity theory to split the shear strain along the different directions. We write
(13)
where the function Γ(τe) is representative of the nonlinear behavior of the traction oil and
(14)
is the equivalent stress. By following the rheological model proposed by Bair and Winer, the function Γ(τe) takes the form
(15)
where τL = τL0 + ap is the limiting shear stress. The estimation of the shear strain is carried out assuming that for hard-EHL conditions, the pressure distribution is close to a Hertzian distribution (except for a peak close to the trailing edge of the contact) and considering that most part of the contact is characterized by an almost constant thickness h of the lubricant film, which, in turn, is calculated on the basis of EHL formulas. Therefore, we can write
(16)
Recalling that the local spin-sliding motion is completely determined as a function of the creep, slip, and spin coefficient, one is able to calculate the quantities μin, μout, χin, χout, and the roller-roller traction coefficient μC by simply integrating the tangential stress over the contact area. Once these quantities are obtained, the efficiency and overall traction performance of the variator are promptly derived (see also [13, 14]).

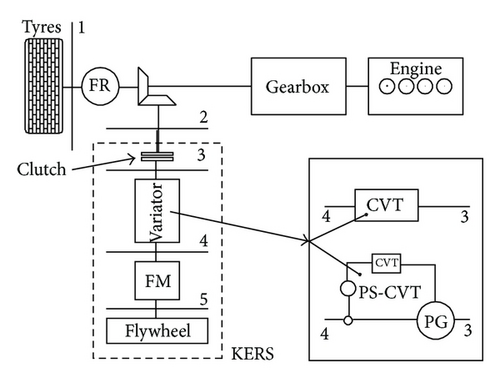
4. Simulation of KERS Behavior

In this section, we employ the mechanical model of the three toroidal traction drives to investigate the overall performance of a mechanical hybrid powertrain. Among all the possible configurations of mechanical hybrid powertrains [7], a flywheel KERS connected into the vehicle propshaft through a friction clutch (see Figure 3) is considered. This configuration gives larger fuel economy improvements than others when it works in synergy with stop and restart system [7]. The simulation has been performed via inverse dynamic simulator of the vehicle powertrain. The driving cycle is given as a velocity pattern, and the driveline parameters are calculated backwards with kinetic, kinematic, and efficiency models. In this paper the focus is on the energy recovery potential of the KERS, and the gearbox and the engine are not included in the model. Further investigation is needed to get the fuel economy and CO2 emissions reduction potential of the KERS. The driveline with KERS, considered in this study, is made of wheels, differential and final drive (FR), KERS driving clutch, toroidal CVT, final step-up drive, and high-speed rotating flywheel. We define two KERS performance indexes: the KERS boost and the round-trip efficiency. In Section 2 of the driveline (see Figure 3), the torque which is necessary to drive the vehicle following the driving schedule is called , which can be positive or negative. The quantity is defined, which is equal to only when , zero otherwise. The torque that is actually given by the KERS in Section 2 is T2, and it can be positive (reuse mode) or negative (recovery mode). Moreover, we define: which is equal to T2 if T2 ≥ 0, zero otherwise; which is equal to T2 if T2 < 0, and zero otherwise. The KERS boost is defined as
(17)
where tcycle  is the time duration of one driving cycle and ω2 is the angular velocity of shaft 2. The KERS boost is the energy given by the KERS to the vehicle propshaft per cycle, divided by the energy that is needed to follow the driving schedule per cycle and calculated in Section 2 of the driveline.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
A schematic picture of the driveline of the mechanical hybrid vehicle. Sections of the driveline are tagged with numbers. FR is the final drive of the vehicle driveline and FM is the final multiplier. The KERS is plugged in the vehicle propshaft through a friction clutch. A second clutch (not shown in the figure) can disconnect the FM from the variable drive when the flywheel is in idle rotation.
The round trip efficiency is calculated as:
(18)
The round trip efficiency is the energy actually given by the KERS into the vehicle propshaft per cycle divided by the energy actually given by the propshaft to the KERS per cycle.

5. Results

In this section, we first present the main traction and efficiency performance of the three investigated toroidal traction drives, and afterwards we focus on the energy recovery efficiency of a KERS geometry based on these kind of transmissions. The fluid properties are reported in Table 1 and the geometrical data of the three variators in Table 2.

Table 1. Fluid properties at T = 99∘C.
Absolute viscosity at the atmospheric pressure η0 = 3.25 × 10−3 Pa s
Viscosity-pressure index Z1 = 0.85
Pressure-viscosity coefficient ζ = 1.71 × 10−8 Pa  −1
Limiting shear stress at atmospheric pressure τL0 = 0.02 × 109 Pa
Limiting shear stress constant a = 0.085
Pole pressure constant of Roelands viscosity model cp = 1.96 × 108 Pa
Pole viscosity of Roelands viscosity model η∞ = 6.31 × 10−5 Pa s
Table 2. The geometric data of the three toroid geometries.
  SHTV SFTV DFTV
Cavity radius r0 40 mm 40 mm 40 mm
Roller radius r2 34.6 mm 40 mm 18.7 mm
Conformity ratio CR = r22/r0 0.8 0.5 0.8
Half-cone angle θ π/3 π/2 π/2
Incidence cone-angle α     43 deg
Aspect ratio k = e/r0 0.625 0.25 0.286
N∘ of cavities m 2 2 2
N∘ of rollers set n 3 3 3
N∘ of rollers per set nr 1 1 2

5.1. Traction Behavior of the DFTV

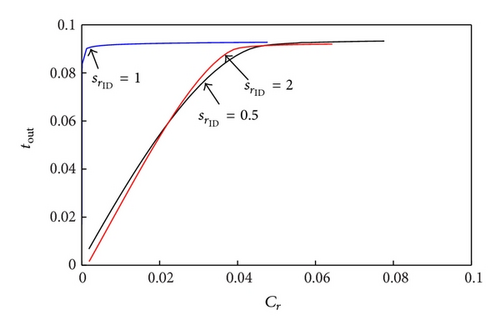
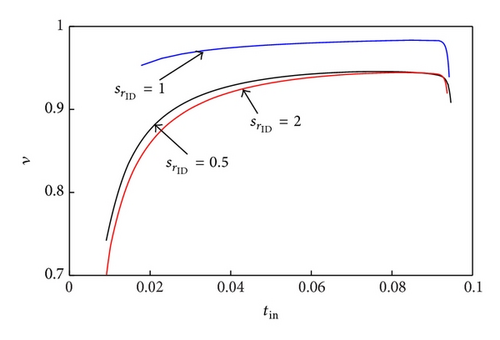
Figure 4 shows the performance in terms of traction and efficiency of the double toroidal traction drive (DFTV). Calculations have been carried out at constant values of the primary speed ω1 = 2000 RPM and normal contact load FN = 20 kN. Interestingly, since the DFTV variator presents negligible values of spin losses at unit ratio (blue curve in Figure 4(a)), in this case the traction curve increases very fast as the creep is increased from zero. However, at different speed ratios (red curve in Figure 4(a)), and (black curve in Figure 4(a)), the presence of spin losses determines a strong decrease of traction versus creep slope. The linear behavior is observed until a creep value Cr = 0.02 is reached, where the traction curve presents a typical knee that corresponds to the maximum achievable value of output dimensionless torque . In Figure 4(b) we show the variator mechanical efficiency ν as a function of the dimensionless input torque tin. It is worth noticing that at , the efficiency takes very high values, equal to about 0.98 on most part of the input torque range. However, as tin (and therefore tout) approaches its limiting value the efficiency rapidly drops because of the fast increase of the creep coefficient. At the extreme ratios: (red curve), (black curve) in Figure 4(b), the trend of the ν versus tin resembles the behavior observed for , but the efficiency values are considerably smaller over the whole torque range, with a maximum value close to 0.94-0.95.

Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
The DFTV variator performance. The dimensionless output torque tout as a function of the overall creep coefficient Cr (a) and the overall mechanical efficiency ν as a function of the input torque coefficient tin (b) for the three geometric ratios ( − black curve,  − blue curve,  − red curve). Calculations are shown for FN = 20 kN.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
The DFTV variator performance. The dimensionless output torque tout as a function of the overall creep coefficient Cr (a) and the overall mechanical efficiency ν as a function of the input torque coefficient tin (b) for the three geometric ratios ( − black curve,  − blue curve,  − red curve). Calculations are shown for FN = 20 kN.

5.2. Comparison of DFTV, SFTV, and SHTV

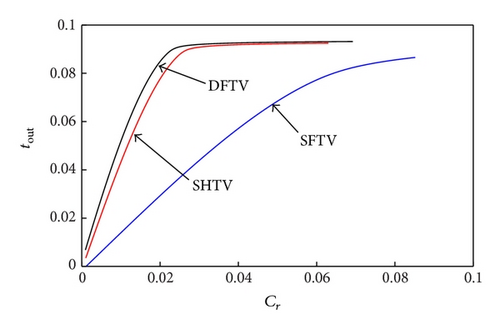
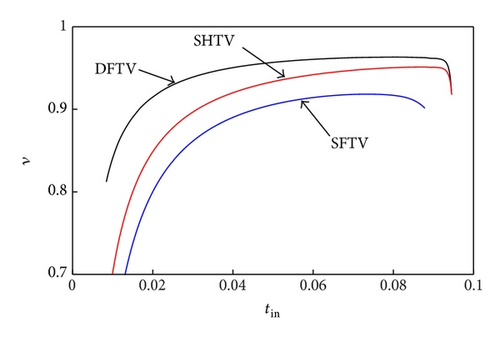
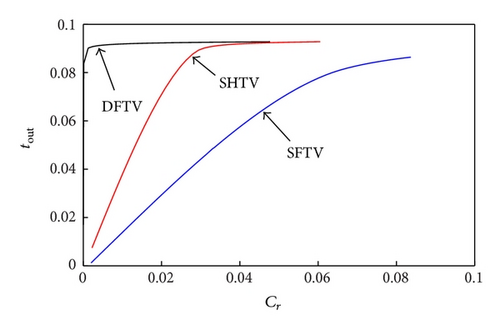
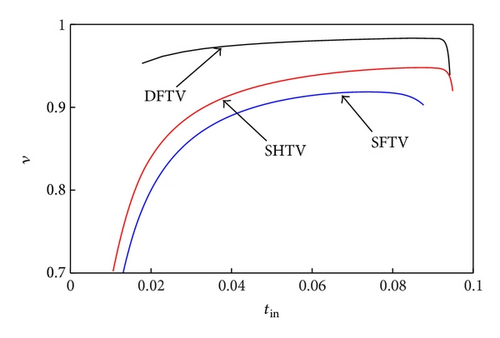
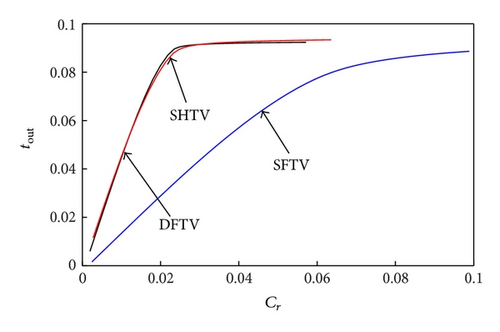
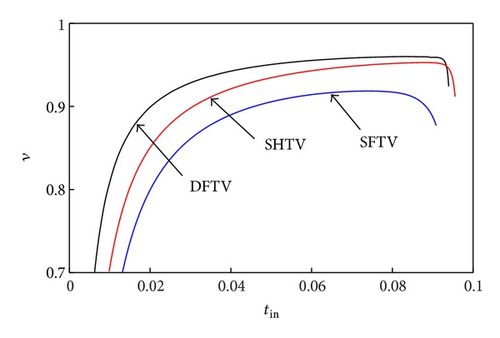
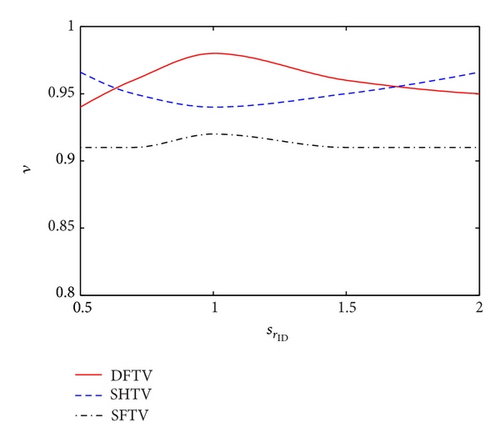
Figure 5 compares quantitatively the different toroidal variators in terms of traction capabilities and efficiency. Calculations have been carried out at given constant values of the primary speed ω1 = 2000 RPM and of the normal load FN = 20 kN. The dimensionless output torque tout is plotted against the overall creep coefficient Cr, whereas the efficiency ν is represented as a function of the input dimensionless torque tin. In all cases, we observe, as expected, an almost linear increase of tout as Cr is increased from zero. However, as the creep increases, the curve starts to deviate from the linear trend and reaches a saturation value in correspondence of the maximum transmissible torque. Interestingly, the slope of the linear part of the three traction curves is different for the three different variators and also changes as the geometric speed ratio is changed. In all cases, the SFTV shows a significantly worse behavior if compared to the other two typologies. More interesting is to compare the SHTV and the DFTV. At ratios and , the two variators show almost the traction capabilities however the DFTV performs significantly better than the SHTV in terms of mechanical efficiency. The DFTV strongly outperforms both in terms of traction and mechanical efficiency the SHTV at geometric speed ratio , as a consequence of the very limited amount of spin motion and spin momentum.

Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
The effective output torque tout as a function of the overall creep coefficient Cr and the overall efficiency ν as a function of the effective input torque , for DFTV, SHTV, and SFTV. Calculations are presented for a normal load FN = 20 kN.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
The effective output torque tout as a function of the overall creep coefficient Cr and the overall efficiency ν as a function of the effective input torque , for DFTV, SHTV, and SFTV. Calculations are presented for a normal load FN = 20 kN.
Details are in the caption following the image
Figure 5 (c)
Open in figure viewerPowerPoint
The effective output torque tout as a function of the overall creep coefficient Cr and the overall efficiency ν as a function of the effective input torque , for DFTV, SHTV, and SFTV. Calculations are presented for a normal load FN = 20 kN.
Details are in the caption following the image
Figure 5 (d)
Open in figure viewerPowerPoint
The effective output torque tout as a function of the overall creep coefficient Cr and the overall efficiency ν as a function of the effective input torque , for DFTV, SHTV, and SFTV. Calculations are presented for a normal load FN = 20 kN.
Details are in the caption following the image
Figure 5 (e)
Open in figure viewerPowerPoint
The effective output torque tout as a function of the overall creep coefficient Cr and the overall efficiency ν as a function of the effective input torque , for DFTV, SHTV, and SFTV. Calculations are presented for a normal load FN = 20 kN.
Details are in the caption following the image
Figure 5 (f)
Open in figure viewerPowerPoint
The effective output torque tout as a function of the overall creep coefficient Cr and the overall efficiency ν as a function of the effective input torque , for DFTV, SHTV, and SFTV. Calculations are presented for a normal load FN = 20 kN.

5.3. KERS Performance

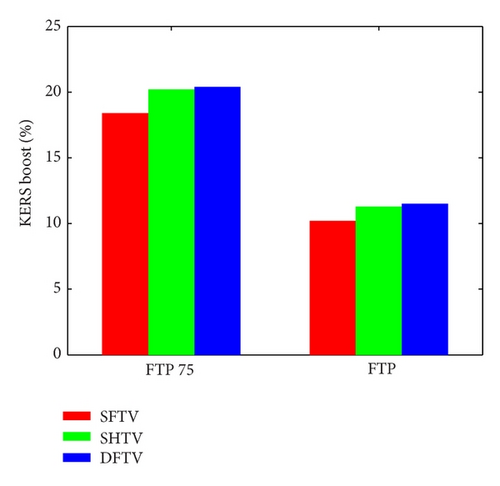
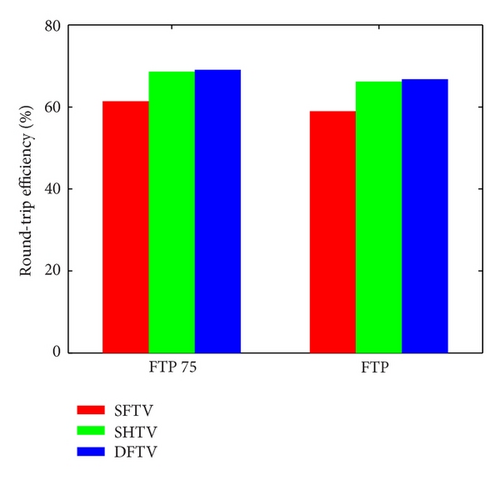
The simulations of KERS performance have been carried out with the data of a typical city car (more details are in [15]). The main features of the KERS device follow. We have considered a CVT KERS mass equal to about 25 kg. The simulations have been performed considering a flywheel with the following characteristics: flywheel inertia Jf = 0.0562 kgm2, flywheel minimum velocity , and flywheel maximum velocity (upper and lower bounds have been chosen according to [17]). The mechanical hybrid under analysis can be exploited for urban driving applications. The maximum energy which can be stored in the flywheel is about 178 kJ that corresponds to the kinetic energy of the vehicle at 60 kph. The simulations have been performed following the urban FTP-75 driving schedule. The driving schedule has been considered as a periodic function which must be followed by the vehicle. The state of charge of the flywheel is the same at the beginning and at the end of the cycle [4]. In order to compare the performance which can be achieved with different variators, for any given toroidal traction drive under investigation, the speed ratio τFM of the final multiplier has been optimized and this optimal value has been used to carry out the simulations. The mechanical efficiencies of DFTV, SHTV, and SFTV have been calculated by means of the analytical models presented in previous sections. We assume that the clamping system allows to control the clamping force in order to optimize the efficiency of the toroidal traction drive for any given speed ratio and the input torque. In order to perform simulations under these working conditions, the efficiency has been calculated with the optimal value of the normalized input torque tin with different speed ratios, and the results are shown in Figure 6. The ratio spread of the three variators is equal to 4, with the speed ratio ranging from to . It is shown that the efficiency of the SFTV is smaller than the efficiency of the DFTV and the SHTV over the entire range of speed ratios. The DFTV outperforms the SHTV only in the intermediate range of speed ratio values. The results of our simulations are shown in Figure 7. The KERS boost (see Figure 7(a)) in the FTP-75 driving schedule is equal to 20.4% with DFTV and 20.2% with SHTV (the difference is almost negligible), whereas it is equal to 18.4% in the case of SFTV. Because SFTV is the one which is currently used in mechanical hybrid systems, our results show that a correct choice of the variator may lead to an improvement of the KERS boost of about 10%. Similar results are shown in FTP driving schedule. In this case, the KERS boost is about 10.2% with SFTV, 11.3% with SHTV, and 11.5% with DFTV. As expected, the best performance are obtained in the urban drive. Figure 7(b) shows the overall round-trip efficiency of the KERS in FTP-75 and FTP driving schedules and a comparison of the results achieved with SFTV, SHTV and DFTV. The round-trip efficiency is not much affected by the driving style, whereas the SFTV efficiency is about 7% smaller in comparison to the DFTV and the SHTV. In our analysis, we have considered a ratio spread close to 4 for all the toroidal traction drives. However, we notice that a variable drive with a larger ratio spread may perform even better provided that the efficiency remains sufficiently high [15]. However, the twofold objective of designing a variator which possesses both large ratio spread and high mechanical efficiency over the entire speed ratio range is a quite challenging task. Different variators may provide different room for further improvement, and, from this point of view, further investigations should deal with the optimization of the design of the DFTV and SHTV for application to KERS.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
The optimal efficiency values of three toroidal CVTs as a function of the speed ratio .
Details are in the caption following the image
Figure 7 (a)
Open in figure viewerPowerPoint
The KERS boost (a) and the KERS round trip efficiency (b) calculated in FTP 75 (urban) and FTP (mixed) driving schedules.
Details are in the caption following the image
Figure 7 (b)
Open in figure viewerPowerPoint
The KERS boost (a) and the KERS round trip efficiency (b) calculated in FTP 75 (urban) and FTP (mixed) driving schedules.

6. Conclusions

We have analyzed the efficiency and traction performance of three toroidal traction drives: the SFTV, the SHTV, and the recently patented DFTV. The latter has been designed in such a way to combine the advantages of the other two existing toroidal geometries and shows enhanced efficiency and traction performance. The DFTV variator consists of a set of counter-rotating conical rollers which are placed into a toroidal cavity; the geometric characteristics of the power rollers allow to reduce the spin losses in a wide range of speed ratios and to get rid of the thrust ball-bearing, which contributes to the torque losses of the half-toroidal type geometry. In order to evaluate the performance of the toroidal traction drives, we have developed a fully flooded isothermal contact model, based on the results of EHL lubrication theory. Our calculations have shown the effectiveness of the DFTV geometric characteristics in terms of reduction of spin losses and improvement of the overall efficiency. The very high mechanical efficiency and traction performance of the DFTV have then been exploited to investigate the performance of a mechanical Kinetic Energy Recovery System (KERS). The energy boost capabilities and the overall round trip efficiency have been calculated for DFTV, SHTV, and SFTV, and a comparison has been discussed. The results have shown that the choice of DFTV and SHTV leads to a very significant increase of the KERS boost capability in urban drive, which is about 10% larger than the result achieved with SFTV.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.