A novel PDE-based image denoising approach is proposed in this paper. One designs here a nonlinear filter for image noise reduction based on the diffusion flow generated by the porous media equation ∂u/∂t = Δβ(u), where β is a nonlinear continuous function of the form β(u) = λu^m, 0 < m < 1. With respect to standard 2D Gaussian smoothing and some nonlinear PDE-based filters, this one is more efficient to remove noise from degraded images and also to reduce “staircasing” effects and preserve the image edges.

1. Introduction

Image noise removal constitutes a very important process, often representing the first step of image analysis [1, 2]. Image denoising with feature preservation represents still a focus in the image processing domain, remaining a serious challenge for researchers. A robust denoising technique has to successfully reduce the amount of noise while preserving the edges and has no blurring effect on the processed image.

The most common noise results from the image acquisition system can be modeled as Gaussian random noise in most cases. Gaussian noise represents statistical noise having the probability density function equal to that of the normal distribution. Numerous image denoising models have been introduced in the past few decades. The conventional filters such as averaging filter, median filter, and 2D Gaussian filter are efficient in smoothing the noise, but also have the disadvantage of blurring image edges [1, 2]. For this reason, some nonlinear image filters, which produce more satisfactory noise reduction results and preserve better the integrity of edges and detail information, were introduced [3].

The nonlinear noise removal techniques based on Partial Differential Equations (PDEs) have been extensively studied in the last two decades [4–6]. The PDE models are the best candidates for a very efficient image denoising. We proposed several robust PDE-based models for noise removal and image restoration in our previous works [7–9]. In this paper we develop a novel PDE-based image denoising approach based on nonlinear diffusion.

The idea of using the diffusion in image processing arose from the use of the Gaussian filter in multiscale image analysis. Nonlinear diffusion methods reduce noise and enhance contours in images [8–11]. Numerous nonlinear PDE denoising approaches based on diffusion have been introduced since the early work of Perona and Malik in 1987 [10]. The anisotropic diffusion developed by them, also called Perona-Malik diffusion, was intended to smooth the image while preserving its edges. Many denoising schemes based on this influential work have been proposed in the last 25 years [10, 11]. More closely of our approach is perhaps Kacur and Mikula scheme [12] which we will briefly present later on.

In the next section of this paper we describe the porous media diffusion filtering model. Then, the explicit version of the fast diffusion filtering scheme is presented in Section 3. Our denoising technique is compared with Perona-Malik scheme and Kacur-Mikula scheme in the fourth section. Other method comparisons and the numerical experiments performed using the proposed approach are discussed in Section 5. The paper ends with a section of conclusions.

2. The Porous Media Diffusion Filtering

Numerous PDE image denoising and segmentation approaches are based on the following nonlinear diffusion equation [10, 11]:

()

where g is the original noised image and u = u(t, x) is the filtered image. Here Ω ⊂ R² is the image domain, ∂Ω is the image boundary, and a : R² → R² is a given continuous and monotone function. Very often, a is a gradient mapping of a = ∇j, where j : R² → Ris a convex continuous function.

To (1) boundary conditions of Dirichlet type: u = 0 on (0, ∞) × ∂Ω or Neumann: a(∇u)υ = 0 on (0, ∞) × ∂Ω are taken. The special case, with

, r = {r₁, r₂}, leads to the so-called total variation model. There is a large variety of nonlinear PDE models inspired by (1) which attempt to eliminate the staircasing effect or to recover images with edges and the total variation model is one of the most efficient. Here we propose a nonlinear filter based on the flow generated by the porous media equation:

()

The function β can be multivalued but maximal monotone, that is, (β(r₁) − β(r₂))(r₁ − r₂) ≥ 0 for all r₁, r₂ ≥ 0 and the range of r → r + β(r) is all of R. This equation is well known as mathematical model for fluid diffusion in porous media and the typical example is β(u) = λ | u|^m−1u where λ > 0 and 0 < m < ∞. The case m > 1 models low diffusion processes and 0 < m < 1 fast diffusion. We note that the model (1) was already used in our previous works for restoring (inpainting) the grayscale images [7, 8].

Given the domain Ω ⊂ R², we denote by L²(Ω), W^k,p(Ω), k = 1,2, 1 ≤ p ≤ ∞, the standard spaces of Lebesgue integrable functions and the Sobolev spaces on Ω. We set H^k(Ω) = W^k,2(Ω),

, and H⁻¹(Ω) the dual space of

with the norm denoting

. Consider here (2) with Dirichlet homogeneous boundary conditions, that is,

()

with u(0, x) = g(x), x ∈ Ω, and β(u(t, x)) = 0 on (0, ∞) × ∂Ω, under the following assumption: β : R → R is monotonically increasing β(0) = 0 and lim _r→±∞β(r) = ±∞.

Here Ω represents a bounded domain of R² with a sufficiently smooth boundary, ∂Ω. By strong solution u = u(t, x) to (3) on [0, T], we mean an absolutely continuous function u : [0, T] → H⁻¹(Ω) such that the strong derivative (du/dt)(t) = lim _ε→0(u(t + ε) − u(t))/ε in H⁻¹(Ω) exists a.e. on (0, T),

a.e. t ∈ (0, T) and

()

where u(0) = g, and the Laplace operator Δ is considered in the sense of distributions on domain Ω. It should be said that a strong solution to (4) is also a weak solution in the classical sense. Let us consider the nonlinear operator A : D(A) ⊂ H⁻¹(Ω) → H⁻¹(Ω) defined by

()

with

and rewrite (4) as the infinite dimensional Cauchy problem:

()

We note [13, 14] that the nonlinear operator is maximal monotone (equivalently, m-accretive) in H⁻¹(Ω) and that it is just the subdifferential ∂φ of the function

()

in the sense of convex analysis. Here, . As a matter of fact, the distribution space H⁻¹(Ω) is the basic functional space to study problem (4). Then, we have the following.

Theorem 1. Let g ∈ H⁻¹(Ω). Then, (4) (equivalently, (6)) has a unique strong solution u : [0, ∞) → H⁻¹(Ω) satisfying

()

Moreover, u is given by the exponential formula

()

It should be recalled (see [13]) that this existence result extends to nonhomogeneous Cauchy problem du/dt + Au(t) = f(t), t ∈ (0, T), u(0) = g.

Theorem 1 is a consequence of the standard existence theory for the infinite dimensional Cauchy problem associated with maximal monotone (m-accretive) operators in Hilbert spaces [13, 14]. It should be emphasized that Theorem 1 applies to (1) as well as to other nonlinear diffusion equations of monotone type arising in the filtering theory. In particular, (9) amounts to saying that the finite difference scheme,

()

where k = [t/h], is convergent to u(t). In the linear case, that is, β(u) = u, this scheme is at origin of high-order Sobolev gradient method developed in [15, 16]. Formula (9) is known in the literature as the Crandall-Liggett exponential formula.

The flow u(t) = S(t)g is a continuous semigroup of contractions in H⁻¹(Ω) in this case or in L¹(Ω), in other situation, and the denoising effect of (6) is due to smoothing effect of S(t) on initial data, a property which is a characteristic to semigroups generated by the nonlinear operators A of the gradient type ∂φ, where φ is a convex and lower semicontinuous function. Since Theorem 1 applies to any initial data g ∈ H⁻¹(Ω), which is a quite general space of distributions on Ω, the filter g → S(t)g can be used for smoothing very noised images g.

It should be emphasized that, for filtering purpose, it suffices to compute u(t) at any time t > 0 since the smoothing effect does not increase with t. On the contrary, since for t → 0 we have [13]

()

where u_∞ is a steady-state solution to A, that is, Au_∞ = 0, one might expect that, for a large t, the filtered image could be far away from the original image g. This means that in the algorithm (10), the best filtered image can be obtained for k → ∞, kh ≈ ε, and ε arbitrarily small. If one wants to restore the image g via step descent algorithm, then (6) should be replaced by

()

or, in its discrete version,

()

because, by (11), lim _t→∞u(t) = u_∞, where Au_∞ + λ(u_∞ − g) = 0, that is,

()

This procedure was used in [7] for restoring and inpainting significantly degraded images g. We also have the generation formula lim _t→0(g − S(t)g)/t = Ag in H⁻¹(Ω). This means that the operator-A is the infinitesimal generator of the semigroup S(t) [12]. The smoothing performance of the filter S(t) and its standard deviation is made precisely below.

Theorem 2. Let g ∈ L¹(Ω) be such that . Then

()

If j(g) ∈ L¹(Ω), then

()

Proof. Formula (15) is immediate by the continuity of the function t → −Δβ(S(t)g) from [0, T] to H⁻¹(Ω). As regards formula (16), we have , for all t ≥ 0, and this yields , for all t ≥ 0, while by equation (d/dτ)S(τ) − Δβ(S(τ)g) = 0, for all τ > 0, we have, by multiplying with β(S(τ)g) in H⁻¹(Ω), , for all t ≥ 0.

We also note that for (4) the maximum principle is also valid. More precisely, we have the following.

Theorem 3. Assume that g ≥ 0, a.e. in Ω. Then, u(t, x) ≥ 0 a.e. (t, x)∈(0, ∞) × Ω.

Proof. We multiply (4) by (β(u)) ⁻ and integrate on (0, t) × Ω to get u⁻ ≡ 0, as claimed.

For denoising procedure, the filter u(t) = S(t)g, generated by (2) in the fast diffusion case, that is, for β(u) = λu^m, 0 < m < 1 (like the classical Gaussian filter), has the disadvantage that it is not localized as in this case the solution u = u(t, x) to (2) propagates with infinite speed. Moreover, u(t) has extinction in a finite time which depends on the norm of g. The situation is different in the low diffusion case β(u) = λu^m, m > 1, where the propagation is with finite speed, and so the denoising flow is localized.

In (2) one might consider the Neumann boundary condition β(∇u)υ = 0 on (0, ∞) × ∂Ω. In this case the operator A is given by (5) where D(A) = {u ∈ L¹(Ω), β(u) ∈ H¹(Ω)} and Theorem 1 remains valid in the present situation; the basic space is H = (H¹(Ω)) ^′ instead of H⁻¹(Ω).

3. The Explicit Scheme of the PDE Algorithm

Now, let us consider the explicit version of the scheme (10), obtained by the fast diffusion model. Namely, u^k+1 = hΔ(u^k−1) ^1/α + u^k, k = 0,1, …, g = u⁰. We take g = g_i,j ≈ g(ih, jh), where i ∈ [1, M] and j ∈ [1, N], and m = 1/α. Thus, the finite difference scheme leads to the following iterative process:

()

where λ = h/4l²,

, and k = 1, …, K.

Using the iterative scheme (17) with some properly selected parameters α, λ, and K, respectively, the initial noised image is successfully filtered in K steps. Therefore, the obtained u^K represents the final image enhancement result. The choice of K in our simulation was dictated by the numerous tests we have performed in specific examples.

A proper selection of the parameter values is very important and cannot be a priori defined. It turns out that the selection of a very large number of iterations, for example, using a K > 40 value, could produce a blurring effect on the processed image, while considering a very small K value, such as K < 5, could result in an unsatisfactory image denoising result. A great K value increases also the computational complexity of this filtering process, producing a much higher computation time.

Also, using a large enough λ value, such as λ > 5, could increase the degradation of the noised image. A very small λ parameter, such as λ < 0.1, produces no visible smoothing results. Obviously, the parameter α must satisfy the condition 1/α ∈ (0,1), for a successfully noise removal.

4. Comparison with Other Noise Removal Techniques

The denoising model discussed above is generated by the minimization problem given by (14), where u ∈ L¹(Ω)∩H⁻¹(Ω) and η is the potential function corresponding to nonlinear diffusivity function β : R → R. The function is a penalty term which forces the restored image u = u(x) to stay close to the initial image g = g(x).

We compared our nonlinear diffusion-based noise removal technique with Perona-Malik denoising scheme [5, 10, 17] and other more general techniques (see [12]). These approaches based on (1) reduces to the minimization problem:

()

The fact that the distance from u to g is taken in the norm

which is considerably weaker than the L²(Ω)-norm considered in the Perona-Malik model as well as in most of the denoising models [9–11] has the advantage that it allows to work with very degraded initial images which practically are not represented by Lebesgue integrable functions but by distributions. However, it should be said that our model has a considerable better smoothing effect than that proposed by Perona and Malik. Indeed, as seen above, the solution u to minimization problem satisfies the nonlinear elliptic equation:

()

with boundary conditions

(or Neumann flux boundary conditions as the basic space is

, the dual of H¹(Ω), instead of

. As seen earlier, the minimization problem can be replaced by the evolution equations (4) or (13)).

This means that ∇β(u) = β^′(u)∇u ∈ L²(Ω) which indicates a smoothing effect comparable with the standard one, but for a suitable choice of β one can avoid the “staircasing” effect which is common in denoising procedure with high smoothing effect.

A reformulation of problem (14) and, implicitly, of the dynamic model (3) allows a closer comparison of this model with that inspired by the Perona-Malik classical denoising technique [10]. If we denote by A₀ : D(A₀) ⊂ L²(Ω) → L²(Ω) the operator A₀u = −Δu,

and recall that A₀ is an isometry from

for

, we can rewrite the minimization problem as

()

where

is the square root of A₀. The Euler-Lagrange optimality condition for variational problem (20) can be expressed as

()

Keeping in mind that

is defined by

()

we may interpret (21) (resp., (20)) in an appropriate sense (1). From this perspective, the denoising model (19) is close to the “total variation model” (1) if β is taken as

()

Indeed, in this case, (21) reduces to

()

However, the present model is more convenient that the “total variation model,” which is constructed in a nonenergetic space (the space of function with bounded variation) and so hard to treat from the computational point of view. As a matter of fact, by the regularization necessary to construct a viable numerical scheme, the “total variation model” loses most of the theoretical advantages regarding the sharp edge detection and elimination of the staircasing effect.

The simulation developed in the next section confirms this important advantage (see the results depicted in Figures 1 and 2). We must emphasize also that there are numerous empirical denoising schemes obtained by modifying the original Perona-Malik model [5, 10, 11, 17–19], most of them not well posed from the mathematical point of view. The Kačur and Mikula denoising model [12] is based on the boundary value problem:

()

with Neumann boundary condition ∇β(x, u) · υ = 0 on (0, T) × Ω.

Details are in the caption following the image — **Figure 1 (a) Original Lena image**
Open in figure viewer PowerPoint

Gaussian noise removal results produced by our technique and other approaches.

Here b(x, ·) and β(x, ·) are continuous and monotonically increasing, g and f are Lipschitzian, and G_σ is a smoothing kernel. In the special case f = 0, g(r) = r, and b, β independent of x problem (25) reduces to (2) with Neumann boundary conditions and β replaced by β · b⁻¹. In general, (25) can be rewritten as

()

with appropriate Neumann boundary conditions. It should be said that in this general form the Cauchy problem for (25) or (26) is not well posed and so the finite difference scheme (10) is not convergent. The model considered here is mathematically well posed. It should be mentioned however that in [12] a semi-implicit scheme is designed which is convergent to a weak solution to (25).

5. Numerical Experiments and Method Comparisons

The PDE-based image denoising technique proposed here has been tested on various image datasets, satisfactory filtering results being obtained. We have filtered hundreds of grayscale images affected by various levels of Gaussian noise using the described approach. An important advantage of our filtering technique is that it performs a robust noise reduction while preserving the image edges [20, 21].

We have obtained the best denoising results for the following set of parameters of the diffusion model provided by formula (18): α = 2, which corresponds to the physical model of diffusion in plasma, λ = 1.5 and N = 20. Some grayscale image reduction examples based on these parameter values are provided in Figures 1 and 2, respectively.

Numerous method comparisons have also been performed. The denoising performance of our method has been compared with performances of other noise removal techniques, such as the 2D Gaussian filter, the averaging filter, and Perona-Malik anisotropic diffusion scheme. From the performed numerical experiments it is obvious that the approach introduced here works better than these well-known filtering algorithms, as one can observe in the figures.

In order to assess the performance levels of each image denoising technique, one computes the norm of the error image. Thus, for any initial image g and its restored version u, having the [M × N] size, the error value is calculated. One can see the values of this norm of the image error parameter in the next tables.

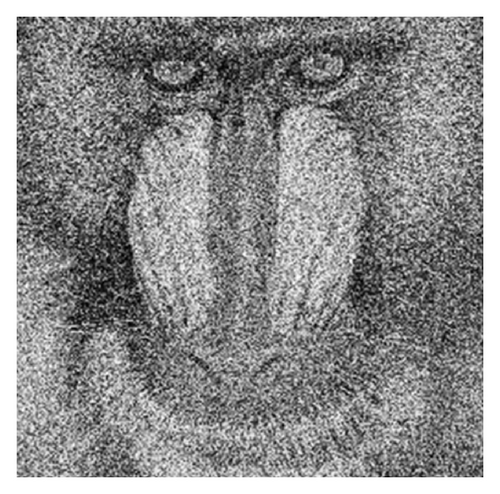
In Figure 1(a), the standard [512 × 512] image of Lena is displayed in the grayscale form. Then, it is corrupted by an amount of Gaussian noise characterized by parameters 0.2 (mean) and 0.02 (variance), the noising result being displayed in Figure 1(b).

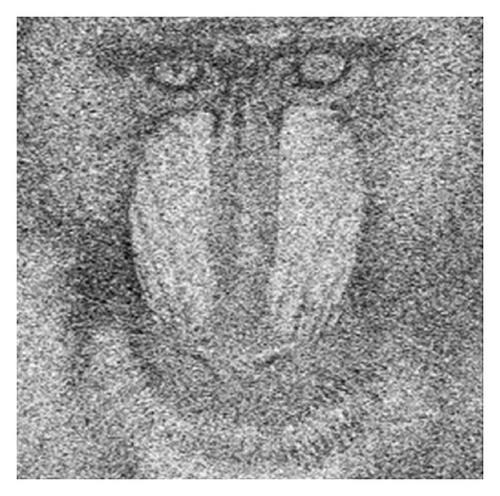
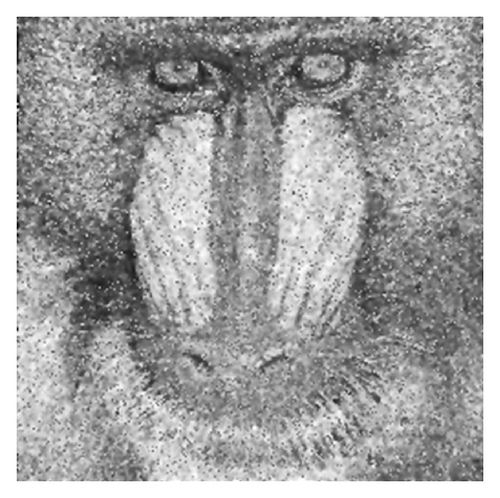
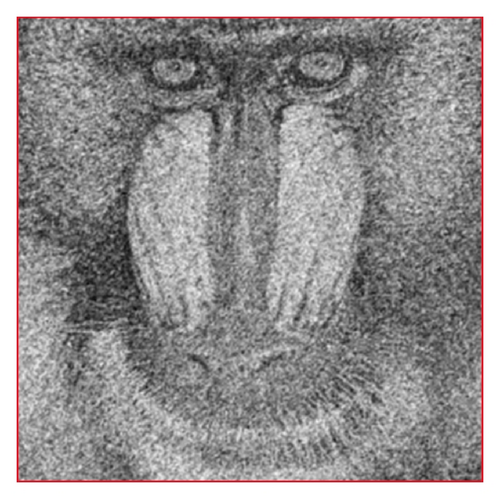
In Figure 1(c) the image denoising result produced by the classic [3 × 3] Gaussian 2D filter kernel is displayed, while the noise reduction obtained with an [3 × 3] averaging filter kernel is represented in Figure 1(d). The noise removal produced by the Perona-Malik approach is displayed in Figure 1(e), while the denoising result provided by the nonlinear PDE model proposed here is represented in Figure 1(f).

The values of the norm of the error image corresponding to all these image filtering methods are displayed in Table 1. One can see that our anisotropic diffusion-based noise reduction approach performs better than the other filters, minimizing the respective error.

Table 1. Values of norm of the error image parameter for various noise reduction approaches.

Denoising technique	Gaussian filter	Average filter	Perona-Malik filter	Proposed AD filter
Norm of the error	6.40 × 10³	6.05 × 10³	6.84 × 10³	5.15 × 10³

Another image denoising method comparison example is displayed in Figure 2. The same noise removal approaches (standard Gaussian, average filtering, Perona-Malik, and our technique) are applied on the standard Baboon image corrupted by the same amount of Gaussian noise, their results being represented in Figures 2(c)–2(f). The corresponding values of the norm of the error image parameter are displayed in Table 2. One can observe the minimum error value obtained by our proposed AD-based noise removal algorithm.

Table 2. Values of norm of the error image parameter for various noise reduction approaches.

Denoising technique	Gaussian filter	Average filter	Perona-Malik filter	Proposed AD filter
Norm of the error	7.20 × 10³	6.14 × 10³	6.55 × 10³	5.36 × 10³

Our filtering algorithm increases the image quality not only by performing a robust Gaussian noise reduction, but also by enhancing the grayscale image contrast. Also, the proposed denoising technique runs quite fast, a [512 × 512] digital image being processed in less than 1 s. The time complexity decreases proportionally with the size of K parameter.

6. Conclusions

A novel PDE-based image noise reduction technique has been proposed in this paper. We have designed a robust nonlinear image filter based on the flow generated by the porous media equation.

The provided nonlinear diffusion-based denoising technique performs successfully for grayscale images corrupted by 2D Gaussian noise, producing also an improved image contrast. Our method is also an edge preserving noise removal technique, which represents an important advantage.

It has been compared with some influential anisotropic diffusion approaches, like that proposed by Perona and Malik [5, 10], the obtained comparison results being very encouraging for us. Also, it provides better smoothing results than many other denoising techniques, while executing almost as fast as them, given its quite low-time complexity.

We have also tested this PDE-based model on other types of image noise and obtained mixed filtering results. While our technique performs somewhat well for images affected by some types of noise such as speckle [9], it does not succeed in removing properly some other types of noise, like salt and pepper. Therefore, designing some robust filters for other types of image noise will represent the focus of our future work in the image processing domain.

Because of its edge-preserving and contrast-enhancing character, the technique described in this paper can be successfully applied in image analysis domains requiring image object emphasizing and detection.

Acknowledgments

This work was mainly supported by the project PN-II-ID-PCE-2011-3-0027-160/5.10.2011 financed by UEFSCDI, Romania. It was supported also by the Institute of Computer Science, The Romanian Academy, Iasi, Romania.

References

1 Jain A. K., Fundamentals of Digital Image Processing, 1989, Prentice Hall, Englewood Cliffs, NJ, USA.
Google Scholar
2 Gonzalez R. and Woods R., Digital Image Processing, 2001, 2nd edition, Prentice Hall, New York, NY, USA.
Google Scholar
3 Nallaperumal K., Selvakumar R. K., Arumugaperumal S., Annam S., and Vishwanath N., Hansa filter: a fuzzy adaptive nonlinear Gaussian filter: an adaptive non local algorithm, International Journal of Imaging and Engineering. (2008) 2, no. 1.
Google Scholar
4 Guichard F., Moisan L., and Morel J.-M., A review of P.D.E. models in image processing and image analysis, Journal de Physique. (2001) 4, 137–154, 2-s2.0-0036509158.
Google Scholar
5 Weickert J., Anisotropic Diffusion in Image Processing, 1998, B. G. Teubner, Stuttgart, Germany, European Consortium for Mathematics in Industry, MR1666943, ZBL0886.68131.
Google Scholar
6 Alvarez L., M.-O. Berger, R. Deriche, I. Herlin, J. Jaffré, and J.-M. Morel, Images and PDE′s, ICAOS ′96 (Paris, 1996), 1996, 219, Springer, London, UK, 3–14, Lecture Notes in Control and Information Sciences, https://doi.org/10.1007/3-540-76076-8_112, MR1430119.
10.1007/3-540-76076-8_112
Google Scholar
7 Barbu T. and Barbu V., A PDE approach to image restoration problem with observation on a meager domain, Nonlinear Analysis: Real World Applications. (2012) 13, no. 3, 1206–1215, ZBL1239.94005, https://doi.org/10.1016/j.nonrwa.2011.09.014, MR2863949.
10.1016/j.nonrwa.2011.09.014
Web of Science® Google Scholar
8 Barbu T., Barbu V., Biga V., and Coca D., A PDE variational approach to image denoising and restoration, Nonlinear Analysis: Real World Applications. (2009) 10, no. 3, 1351–1361, ZBL1169.35341, 2-s2.0-60549102447, https://doi.org/10.1016/j.nonrwa.2008.01.017.
10.1016/j.nonrwa.2008.01.017
Web of Science® Google Scholar
9 Barbu T., A PDE based model for sonar image and video denoising, AnAlele Stiintifice Ale Universitatii Ovidius, Constanta, Seria Matematica. (2011) 19, no. 3, 51–58.
Web of Science® Google Scholar
10 Perona P. and Malik J., Scale-space and edge detection using anisotropic diffusion, Proceedings of IEEE Computer Society Workshop on Computer Vision, 1987, 16–27.
Google Scholar
11 Catte F., Lions P. L., Morel J.-M., and Coll T., Image selective smoothing and edge detection by nonlinear diffusion, SIAM Journal on Numerical Analysis. (1992) 29, no. 1, 182–193, ZBL0746.65091, 2-s2.0-0026821645.
10.1137/0729012
Web of Science® Google Scholar
12 Kačur J. and Mikula K., Slow and fast diffusion effects in image processing, Computing and Visualization in Science. (2001) 13, no. 4, 185–195, https://doi.org/10.1007/s007910000047.
10.1007/s007910000047
Google Scholar
13 Barbu V., Nonlinear Differential Equations of Montone Type in Banach Spaces, 2010, Springer, New York, NY, USA.
10.1007/978-1-4419-5542-5
Google Scholar
14 Brezis H., E. Zarantonello, Monotonicity methods in Hilbert spaces and some applications to nonlinear partial differential equations, Contributions to Nonlinear Functional Analysis, 1971, Acdemic Press, New York, NY, USA.
10.1016/B978-0-12-775850-3.50009-1
Google Scholar
15 Calder J., Mansouri A., and Yezzi A., New possibilities in image diffusion and sharpening via high-order Sobolev gradient flows, Journal of Mathematical Imaging and Vision. (2011) 40, no. 3, 248–258, 2-s2.0-79953205514, https://doi.org/10.1007/s10851-010-0250-2.
10.1007/s10851-010-0250-2
Web of Science® Google Scholar
16 Calder J., Mansouri A., and Yezzi A., Image sharpening via Sobolev gradient flows, SIAM Journal on Imaging Sciences. (2010) 3, no. 4, 981–1014, ZBL1202.94019, https://doi.org/10.1137/090771260, MR2763705.
10.1137/090771260
Web of Science® Google Scholar
17 Jin Z. and Yang X., Strong solutions for the generalized Perona-Malik equation for image restoration, Nonlinear Analysis: Theory, Methods and Applications. (2010) 73, no. 4, 1077–1084, ZBL1194.35503, 2-s2.0-77955321879, https://doi.org/10.1016/j.na.2010.04.039.
10.1016/j.na.2010.04.039
Web of Science® Google Scholar
18 Black M. J., Sapiro G., Marimont D. H., and Heeger D., Robust anisotropic diffusion, IEEE Transactions on Image Processing. (1998) 7, no. 3, 421–432, 2-s2.0-0032023715.
10.1109/83.661192
CAS PubMed Web of Science® Google Scholar
19 Weickert J., ter Haar Romeny B. M., and Viergever M. A., Efficient and reliable schemes for nonlinear diffusion filtering, IEEE Transactions on Image Processing. (1998) 7, no. 3, 398–410, 2-s2.0-0032026465.
10.1109/83.661190
CAS PubMed Web of Science® Google Scholar
20 Kim S. and Lim H., A non-convex diffusion model for simultaneous image denoising and edge enhancement, 15, Proceedings of the 6th Mississippi State-UBA Conference on Differential Equations and Computational Simulations, 2007, San Marcos, Tex, USA, Southwest Texas State Univ., 175–192, Electron. J. Differ. Equ. Conf., MR2316139.
Google Scholar
21 Acton S. T., Edge enhancement of infrared imagery by way of the anisotropic diffusion pyramid, 1, Proceedings of IEEE International Conference on Image Processing (ICIP ′96), September 1996, Lausanne, Switzerland, 865–868, 2-s2.0-0030401435.
Google Scholar

Citing Literature

All articles

Variational Image Denoising Approach with Diffusion Porous Media Flow

Abstract

1. Introduction

2. The Porous Media Diffusion Filtering

3. The Explicit Scheme of the PDE Algorithm

4. Comparison with Other Noise Removal Techniques

5. Numerical Experiments and Method Comparisons

6. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Variational Image Denoising Approach with Diffusion Porous Media Flow

Abstract

1. Introduction

2. The Porous Media Diffusion Filtering

3. The Explicit Scheme of the PDE Algorithm

4. Comparison with Other Noise Removal Techniques

5. Numerical Experiments and Method Comparisons

6. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information