The matrix equation which includes some frequently investigated matrix equations as its special cases, plays important roles in the system theory. In this paper, we propose an iterative algorithm for solving the quaternion matrix equation over generalized (P, Q)-reflexive matrices. The proposed iterative algorithm automatically determines the solvability of the quaternion matrix equation over generalized (P, Q)-reflexive matrices. When the matrix equation is consistent over generalized (P, Q)-reflexive matrices, the sequence {X(k)} generated by the introduced algorithm converges to a generalized (P, Q)-reflexive solution of the quaternion matrix equation. And the sequence {X(k)} converges to the least Frobenius norm generalized (P, Q)-reflexive solution of the quaternion matrix equation when an appropriate initial iterative matrix is chosen. Furthermore, the optimal approximate generalized (P, Q)-reflexive solution for a given generalized (P, Q)-reflexive matrix X₀ can be derived. The numerical results indicate that the iterative algorithm is quite efficient.

1. Introduction and Notations

Quaternion matrix equation is one of the topics of very active research in matrix theory and applications, and some important results have been developed. For example, Kyrchei [1] derived the explicit representation formulas for the minimum norm least squares solutions of quaternion matrix equations AX = B, XA = B, AXB = D. Yuan and Liao [2] derived the expressions of the least squares (j-self-conjugate) solution with the least norm of the quaternion matrix equation . Song et al. [3] obtained the expressions of the explicit solutions of quaternion matrix equations XF − AX = BY and . He and Wang [4] studied the necessary and sufficient conditions for the existence of a solution to the quaternion matrix equation A₁X + (A₁X) ^η* + B₁Y(B₁) ^η* + C₁Z(C₁) ^η* = D₁ and derived a general solution when the equation is solvable.

The definition of generalized (P, Q)-reflexive matrix can be found in [5]. A complex matrix A is called (P, Q)-generalized reflexive (generalized anti-reflexive) if A = PAQ (A = −PAQ), where P and Q are two generalized reflection matrices; that is, P = P^H = P⁻¹ and Q = Q^H = Q⁻¹. The generalized (P, Q)-reflexive matrices have been widely used in engineering and scientific computations [5–7]. Throughout, we use to denote the set of m × n generalized (P, Q)-reflexive quaternion matrices.

The iterative method is a very important method to solve matrix equations. Peng et al. [8, 9] constructed iteration methods to solve the symmetric and reflexive solutions of matrix equations A₁XB₁ = C₁, A₂XB₂ = C₂. Ding and Chen [10, 11] developed iterative methods for solving a wide variety of matrix equations, based on the hierarchical identification principle [12]. Peng [13–15] presented several efficient iterative methods to solve the constrained least squares solutions of linear matrix equations AXB = C and AXB + CYD = E, by using Paige′s algorithm [16] as the frame method. Wang et al. [17] proposed iterative algorithms for solving the matrix equation AXB + CX^TD = E. Xie et al. [18] presented a gradient based iterative algorithm for solving

()

In [19], Li et al. proposed iterative algorithms to solve the minimal norm least squares solution to (1). Duan et al. [20–24] proposed iterative algorithms for the (Hermitian) positive definite solutions of some nonlinear matrix equations. Dehghan and Hajarian constructed iterative algorithms to solve several linear matrix equations over (anti-)reflexive [25, 26], generalized centrosymmetric [27, 28], and generalized bisymmetric [29, 30] matrices. Recently, Wu et al. [31–35] proposed iterative algorithms for solving various complex matrix equations. Wang et al. [36] derived an iterative method for finding the minimum-norm solution of the QLS problem in quaternionic quantum theory.

However, to our best knowledge, the generalized (P, Q)-reflexive solution of (1) over the quaternion algebra ℍ has not been considered so far. Due to the noncommutativity of ℍ, some well-known equalities for complex and real matrices no longer hold for quaternion matrices, which make the study of quaternion matrix equation more complex than that of real and complex equation. Motivated by the work mentioned previously and keeping the interests and wide applications of quaternion matrices in view (e.g., [37–47]), we, in this paper, consider an iterative method for the following two problems.

Problem 1. For given matrices A_l, C_s ∈ ℍ^p×n, B_l, D_s ∈ ℍ^n×q, l = 1,2, …, u, s = 1,2, …, v, F ∈ ℍ^p×q, and the generalized reflection matrices P ∈ ℍ^n×n, Q ∈ ℍ^n×n, find that , such that

()

Problem 2. When Problem 1 is consistent, let its solution set be denoted by S_X. For a given (P, Q)-reflexive matrix , find , such that

()

The matrix equation (2) plays important roles in the system theory [48–50]. Moreover, (2) obviously includes the matrix equations AXB + CX^TD = F, AX + X^TD = F, and AXB = C as special cases, which have been investigated in [17, 28, 36, 51–53].

Throughout this paper, ℝ^m×n and ℍ^m×n represent the set of all m × n real matrices and the set of all m × n matrices over the quaternion algebra ℍ = {a₁ + a₂i + a₃j + a₄k∣i² = j² = k² = ijk = −1, a₁, a₂, a₃, a₄ ∈ ℝ}. We use A^H, A^T, , tr (A), R(A), Re(A), and vec (A) to denote the conjugate transpose, the transpose, the conjugate, the trace, the column space, the real part, and the mn × 1 vector formed by the vertical concatenation of the respective columns of a matrix A; respectively. We use ∥A∥ to denote the Frobenius norm of A, that is, . The Kronecker matrix product and Hadamard matrix product of the matrices A and B are denoted by A ⊗ B and A⊙B. We use I to denote the identity matrix with the appropriate size.

2. Preliminaries

In this section, we provide some results which will play important roles in this paper.

Firstly, we recall the definition of real inner product space. Then we define a real inner product in the space ℍ^m×n over the field ℝ.

Definition 3 (see [54].)A real inner product space is a vector space V over the real field ℝ together with an inner product defined by a mapping

()

satisfying the following three axioms for all vectors x, y, z ∈ V and all scalars a ∈ ℝ.

(1)
Symmetry: 〈x, y〉 = 〈y, x〉;
(2)
Linearity in the first argument: 〈ax, y〉 = a〈x, y〉, 〈x + y, z〉 = 〈x, z〉 + 〈y, z〉;
(3)
Positive definiteness: 〈x, x〉 > 0 for all x ≠ 0.

In [33–35], the following real inner product was presented to solve some complex matrix equations:

()

for A, B ∈ ℂ^m×n. It is easy to verify that if we let A, B ∈ ℍ^m×n, (5) also defines a real inner product in ℍ^m×n over ℝ. We denote this real inner product space by (ℍ^m×n, ℝ, 〈·, ·〉). From the equalities

()

we know that the induced matrix norm by the introduced inner product 〈·, ·〉 is exactly the Frobenius norm. For convenience, we still use ∥·∥ to denote the induced matrix norm. Let E_ij denote the m × n matrix whose (i, j) entry is 1, and the other elements are zeros. In inner product space (ℍ^m×n, ℝ, 〈·, ·〉), it is easy to verify that E_ij, E_iji, E_ijj, E_ijk, i = 1,2, …m, j = 1,2, …n, is an orthonormal basis, which reveals that the dimension of the inner product space (ℍ^m×n, ℝ, 〈·, ·〉) is 4 mn.

Next, we introduce the well-known real representation of a quaternion matrix. For an arbitrary quaternion matrix M = M₁ + M₂i + M₃j + M₄k ∈ ℍ^m×n, a map ϕ(·), from ℍ^m×n to ℝ^4m×4n, can be defined as

()

Let M and N be two arbitrary quaternion matrices with appropriate size. We know that ϕ(·) satisfies the following properties:

()

It follows a simple verification that ϕ(·) also satisfies the following two properties which is useful for some deduction in this paper:

()

where

()

and E is a matrix whose elements are all equal to one with the same size as M.

Finally, we recall some results about the commutation matrix. A commutation matrix P(m, n) is a mn × mn matrix which has the following explicit form:

()

Moreover, P(m, n) is a permutation matrix and P(m, n) = P^T(n, m) = P⁻¹(n, m). We have the following lemmas on the commutation matrix.

Lemma 4 (see [55].)Let A be an m × n matrix. There is a commutation matrix P(m, n) such that

()

Lemma 5 (see [55].)Let A be an m × n matrix and B a p × q matrix. There exist two commutation matrices P(m, p) and P(n, q) such that

()

3. An Iterative Algorithm for Solving Problem 1

In this section, we firstly construct an algorithm for solving Problem 1. Then we show that if the problem is consistent, the sequence {X(k)} generated by the introduced algorithm converges to a solution of Problem 1 within at most 4pq iteration steps.

Algorithm 6. (1) Input matrices A_l,C_s ∈ ℍ^p×n, B_l, D_s ∈ ℍ^n×q, l = 1,2, …, u, s = 1,2, …, v, F ∈ ℍ^p×q, generalized reflection matrices P ∈ ℍ^n×n, Q ∈ ℍ^n×n, .

(2) Calculate

()

(3) If R(k) = 0, or R(k) ≠ 0 and T(k) = 0, stop; otherwise k : = k + 1.

(4) Calculate

()

(5) Go to Step (3).

The following Lemmas show some properties of Algorithm 6.

Lemma 7. The sequences {R(i)}, {S(i)}, and {T(i)} generated by Algorithm 6 satisfy

()

Proof. One has the following:

()

Therefore, the conclusion (19) holds. Consider

()

Therefore, the conclusion (20) holds.

Lemma 8. Assume that the sequences {R(i)} and {T(i)} are generated by Algorithm 6, and then 〈R(i), R(j)〉 = 0 and 〈T(i), T(j)〉 = 0 for i, j = 1,2, …, i ≠ j.

Proof. Since 〈R(i), R(j)〉 = 〈R(j), R(i)〉 and 〈T(i), T(j)〉 = 〈T(j), T(i)〉 for i, j = 1,2, …, we only need to prove that 〈R(i), R(j)〉 = 0 and 〈T(i), T(j)〉 = 0 for 1 ≤ i < j.

Now we prove this conclusion by induction.

First, we prove

()

When i = 1, from Lemma 7 we have

()

From Lemma 7 and conclusion (24), we have

()

Now assume that conclusion (23) holds for 1 ≤ i ≤ t − 1; from Lemma 7, we have

()

From Lemma 7 and conclusion (26), it can also be obtained that

()

Therefore, by the principle of induction, conclusion (23) holds.

Next, assume that 〈R(i), R(i + r)〉 = 0 and 〈T(i), T(i + r)〉 = 0 for i ≥ 1 and r ≥ 1. We will prove that

()

In order to prove conclusion (28), we first prove that

()

From Lemma 7 we have

()

From Lemma 7 and conclusion (30), we have

()

Also we have

()

Repeating the previous process (32), we have

()

Combining these two relations with (30) and (31), it implies that (28) holds. So, by the principle of induction, we know that Lemma 8 holds.

Lemma 9. When Problem 1 is consistent, let be its solution; then, for any generalized (P, Q)-reflexive initial matrix , the sequences {R(i)}, {T(i)} and {X(i)} generated by Algorithm 6 satisfy

()

Proof. When i = 1, it follows from Algorithm 6 that

()

This implies that (34) holds for i = 1.

Assume that (34) holds for i = t, and then, when i = t + 1,

()

Therefore, Lemma 9 holds by the principle of induction.

Remark 10. Lemma 9 implies that if there exists a positive integer i such that R(i) ≠ 0 and T(i) = 0, then Problem 1 is not consistent. Therefore, the solvability of Problem 1 can be determined by Algorithm 6 in the absence of round-off errors.

From Lemmas 8 and 9, we have the following theorem.

Theorem 11. Assume that Problem 1 is consistent, and then using Algorithm 6 for any generalized (P, Q)-reflexive initial matrix , a solution of Problem 1 can be obtained within finite iteration steps in the absence of round-off errors.

Proof. If R(i) ≠ 0, i = 1,2, …, 4pq, from Lemma 9 we can obtain T(i) ≠ 0, i = 1,2, …, 4pq. Thus R(4pq + 1) and T(4pq + 1) can be computed by Algorithm 6. According to Lemma 8, we have 〈R(i), R(j)〉 = 0, i, j = 1,2, …, 4pq. Considering that the inner product space (ℍ^p×q, ℝ, 〈·, ·〉) is 4pq-dimensional, we know that the set of R(1), R(2), …, R(4pq) is an orthogonal basis of the inner product space (ℍ^p×q, ℝ, 〈·, ·〉). Also from Lemma 8, we have 〈R(i), R(4pq + 1)〉 = 0 for i = 1,2, …, 4pq, which implies that R(4pq + 1) = 0; that is, X(4pq + 1) is a solution of Problem 1.

4. The Solution of Problem 2

In this section, we will prove that the sequence {X(k)} generated by Algorithm 6 converges to the least Frobenius norm generalized (P, Q)-reflexive solution of the quaternion matrix equation when an appropriate initial iterative matrix is chosen. Then, we solve Problem 2 by finding the least Frobenius norm generalized (P, Q)-reflexive solution of a new constructed quaternion matrix equation.

Lemma 12 (see [51].)Assume that the consistent system of linear equations My = b has a solution y₀ ∈ R(M^T); then, y₀ is the unique least Frobenius norm solution of the system of linear equations.

Lemma 13. If Problem 1 is consistent, then the following system of real linear equations is consistent:

()

Furthermore, if the solution sets of Problem 1 and (37) are denoted by S_X and S_Y, respectively, then,

()

Proof. If Problem 1 is consistent, let X be a solution of Problem 1, then we have and PXQ = X, which implies that X is a solution of quaternion matrix equations

()

By (8), (9), and (12), we can derive that the quaternion matrix equations (39) is equivalent to the following real matrix equations:

()

By the operation properties of vec (·), ⊗, ⊙, and Lemma 4, it is not difficult to verify that matrix equations (40) is equivalent to

()

which implies that vec (ϕ(X)) is a solution of (37). So system of real linear equations (37) is consistent.

From the previous procedure, the proof of (38) is trivial.

Theorem 14. If is a solution of Problem 1 and can be expressed as the following form:

()

then,

is the least Frobenius norm solution of Problem 1.

Proof. By (8), (9), (10), and (12) and Lemmas 4 and 5, we have

()

By Lemma 12,

is the least Frobenius norm solution of (37).

Noting (11), we derive from Lemma 13 that is the least Frobenius norm solution of Problem 1.

Remark 15. From Algorithm 6, we can derive that if we choose , G ∈ ℍ^p×q, as the initial iteration matrix, then all X(k) generated by Algorithm 6 have a form of

()

Theorem 16. When Problem 1 is consistent, if we choose the following matrix as the initial iteration matrix

()

where G ∈ ℍ^p×q is arbitrary, or especially, X(1) = 0, then the solution X^*, generated by Algorithm 6, is exactly the least Frobenius norm solution of Problem 1.

From conclusion (44) and Theorem 14, the proof of Theorem 16 is trivial.

Now we consider Problem 2. When Problem 1 is consistent, the solution set of Problem 1 S_X is not empty. For a given generalized (P, Q)-reflexive matrix

, let

; then the least Frobenius norm generalized (P, Q)-reflexive solution of the following quaternion matrix equation is exactly the solution of

()

According to Theorem 16, if we choose the initial iteration matrix

, where G ∈ ℍ^p×q is arbitrary, or especially, choosing

, the least Frobenius norm generalized (P, Q)-reflexive solution

of (46) can be obtained. Then the solution of Problem 2 is

5. Examples

In this section, we give two examples to illustrate the performance of the proposed algorithm.

Example 17. Consider the quaternion matrix equation

()

with the matrices

()

We apply Algorithm 6 to find the generalized (P, Q)-reflexive solution of (47), where

()

are two generalized reflection matrices. Choosing an initial matrix

()

we obtain that the sequence {X(k)} after 21 steps is

()

with ∥R(21)∥ = 2.047 × 10⁻¹³. The obtained results are presented in Figure 1, where r(k) = ∥R(k)∥.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The curve for the Frobenius norm of the residuals from Example 17.

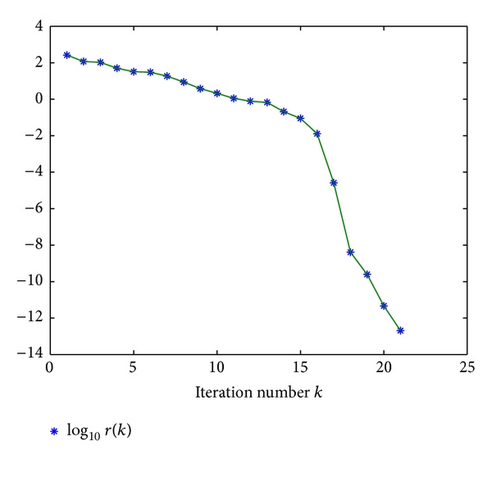
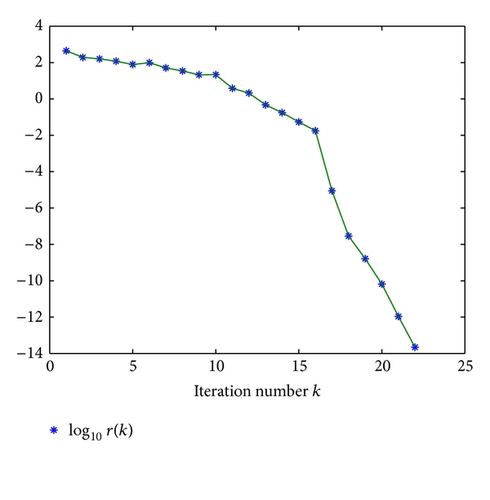
Example 18. Let

()

Now we consider Problem 2, that is, finding the optimal approximate generalized (P, Q)-reflexive solution of the quaternion matrix equation (47) to X₀. Applying Algorithm 6 to (46) by choosing the initial matrix

, we obtain that the sequence {X(k)} after 22 steps is

()

with

. The obtained results are presented in Figure 2, where

So we can obtain the solution of Problem 2; that is,

()

6. Conclusions

In this paper, an algorithm has been presented for solving the quaternion matrix equation over generalized (P, Q)-reflexive matrices. It has been proven that when the quaternion matrix equation is consistent over generalized (P, Q)-reflexive matrices, for any generalized (P, Q)-reflexive initial iterative matrix, the sequence {X(k)} generated by Algorithm 6 will converge to a generalized (P, Q)-reflexive solution within finite iteration steps in the absence of round-off errors. We have also proven that by choosing a suitable initial iterative matrix, the sequence {X(k)} will converge to the least Frobenius norm generalized (P, Q)-reflexive solution of the quaternion matrix equation . Then, by using Algorithm 6, we solved Problem 2. The numerical results have shown that the presented algorithm is quite effective.

Acknowledgments

This research was supported by the grants from the Innovation Program of Shanghai Municipal Education Commission (13ZZ080), the National Natural Science Foundation of China (11171205), and the Natural Science Foundation of Shanghai (11ZR1412500).

References

1 Kyrchei I., Explicit representation formulas for the minimum norm least squares solutions of some quaternion matrix equations, Linear Algebra and its Applications. (2013) 438, no. 1, 136–152, https://doi.org/10.1016/j.laa.2012.07.049, MR2993371, ZBL1255.15022.
10.1016/j.laa.2012.07.049
Web of Science® Google Scholar
2 Yuan S. and Liao A., Least squares solution of the quaternion matrix equation with the least norm, Linear and Multilinear Algebra. (2011) 59, no. 9, 985–998, https://doi.org/10.1080/03081087.2010.509928, MR2826067, ZBL1228.65072.
10.1080/03081087.2010.509928
Web of Science® Google Scholar
3 Song C., Chen G., and Wang X., On solutions of quaternion matrix equations XF − AX = BY and , Acta Mathematica Scientia B. (2012) 32, no. 5, 1967–1982, https://doi.org/10.1016/S0252-9602(12)60153-2, MR2960763.
10.1016/S0252-9602(12)60153-2
Web of Science® Google Scholar
4 He Z.-H. and Wang Q.-W., A real quaternion matrix equation with applications, Linear and Multilinear Algebra. (2013) 61, no. 6, 725–740, https://doi.org/10.1080/03081087.2012.703192, MR3005652.
10.1080/03081087.2012.703192
Web of Science® Google Scholar
5 Chen H.-C. and Sameh A. H., A matrix decomposition method for orthotropic elasticity problems, SIAM Journal on Matrix Analysis and Applications. (1989) 10, no. 1, 39–64, https://doi.org/10.1137/0610004, MR976151, ZBL0669.73010.
10.1137/0610004
Web of Science® Google Scholar
6 Chen H.-C., Generalized reflexive matrices: special properties and applications, SIAM Journal on Matrix Analysis and Applications. (1998) 19, no. 1, 140–153, https://doi.org/10.1137/S0895479895288759, MR1609944, ZBL0910.15005.
10.1137/S0895479895288759
Web of Science® Google Scholar
7 Datta L. and Morgera S. D., On the reducibility of centrosymmetric matrices—applications in engineering problems, Circuits, Systems, and Signal Processing. (1989) 8, no. 1, 71–96, https://doi.org/10.1007/BF01598746, MR998028.
10.1007/BF01598746
Web of Science® Google Scholar
8 Peng Z.-h., Hu X.-y., and Zhang L., An efficient algorithm for the least-squares reflexive solution of the matrix equation A₁XB₁ = C₁, A₂XB₂ = C₂, Applied Mathematics and Computation. (2006) 181, no. 2, 988–999, https://doi.org/10.1016/j.amc.2006.01.071, MR2269978, ZBL1115.65048.
10.1016/j.amc.2006.01.071
Web of Science® Google Scholar
9 Peng Y.-X., Hu X.-Y., and Zhang L., An iterative method for symmetric solutions and optimal approximation solution of the system of matrix equations A₁XB₁ = C₁, A₂XB₂ = C₂, Applied Mathematics and Computation. (2006) 183, no. 2, 1127–1137, https://doi.org/10.1016/j.amc.2006.05.124, MR2294070, ZBL1134.65032.
10.1016/j.amc.2006.05.124
Web of Science® Google Scholar
10 Ding F. and Chen T., Gradient based iterative algorithms for solving a class of matrix equations, IEEE Transactions on Automatic Control. (2005) 50, no. 8, 1216–1221, https://doi.org/10.1109/TAC.2005.852558, MR2156053.
10.1109/TAC.2005.852558
Web of Science® Google Scholar
11 Ding F. and Chen T., On iterative solutions of general coupled matrix equations, SIAM Journal on Control and Optimization. (2006) 44, no. 6, 2269–2284, https://doi.org/10.1137/S0363012904441350, MR2248183, ZBL1115.65035.
10.1137/S0363012904441350
Web of Science® Google Scholar
12 Ding F. and Chen T., Hierarchical gradient-based identification of multivariable discrete-time systems, Automatica. (2005) 41, no. 2, 315–325, https://doi.org/10.1016/j.automatica.2004.10.010, MR2157667, ZBL1073.93012.
10.1016/j.automatica.2004.10.010
Web of Science® Google Scholar
13 Peng Z.-Y., A matrix LSQR iterative method to solve matrix equation AXB = C, International Journal of Computer Mathematics. (2010) 87, no. 8, 1820–1830, https://doi.org/10.1080/00207160802516875, MR2665753, ZBL1195.65056.
10.1080/00207160802516875
Web of Science® Google Scholar
14 Peng Z.-y., New matrix iterative methods for constraint solutions of the matrix equation AXB = C, Journal of Computational and Applied Mathematics. (2010) 235, no. 3, 726–735, https://doi.org/10.1016/j.cam.2010.07.001, MR2719811, ZBL1206.65145.
10.1016/j.cam.2010.07.001
Web of Science® Google Scholar
15 Peng Z.-Y., Solutions of symmetry-constrained least-squares problems, Numerical Linear Algebra with Applications. (2008) 15, no. 4, 373–389, https://doi.org/10.1002/nla.578, MR2413779, ZBL1212.65181.
10.1002/nla.578
Web of Science® Google Scholar
16 Paige C. C., Bidiagonalization of matrices and solutions of the linear equations, SIAM Journal on Numerical Analysis. (1974) 11, 197–209, MR0341842, https://doi.org/10.1137/0711019.
10.1137/0711019
Web of Science® Google Scholar
17 Wang M., Cheng X., and Wei M., Iterative algorithms for solving the matrix equation AXB + CX^TD = E, Applied Mathematics and Computation. (2007) 187, no. 2, 622–629, https://doi.org/10.1016/j.amc.2006.08.169, MR2323068, ZBL1121.65048.
10.1016/j.amc.2006.08.169
Web of Science® Google Scholar
18 Xie L., Ding J., and Ding F., Gradient based iterative solutions for general linear matrix equations, Computers & Mathematics with Applications. (2009) 58, no. 7, 1441–1448, https://doi.org/10.1016/j.camwa.2009.06.047, MR2555281, ZBL1189.65083.
10.1016/j.camwa.2009.06.047
Web of Science® Google Scholar
19 Li Z.-Y., Wang Y., Zhou B., and Duan G.-R., Least squares solution with the minimum-norm to general matrix equations via iteration, Applied Mathematics and Computation. (2010) 215, no. 10, 3547–3562, https://doi.org/10.1016/j.amc.2009.10.052, MR2578938, ZBL1186.65047.
10.1016/j.amc.2009.10.052
Web of Science® Google Scholar
20 Duan X., Liao A., and Tang B., On the nonlinear matrix equation , Linear Algebra and its Applications. (2008) 429, no. 1, 110–121, https://doi.org/10.1016/j.laa.2008.02.014, MR2419144, ZBL1148.15012.
10.1016/j.laa.2008.02.014
Web of Science® Google Scholar
21 Duan X. and Liao A., On the nonlinear matrix equation X + A^* X^−qA = Q(q ≥ 1), Mathematical and Computer Modelling. (2009) 49, no. 5-6, 936–945, https://doi.org/10.1016/j.mcm.2008.10.009, MR2495010, ZBL1165.15302.
10.1016/j.mcm.2008.10.009
Google Scholar
22 Duan X. and Liao A., On Hermitian positive definite solution of the matrix equation , Journal of Computational and Applied Mathematics. (2009) 229, no. 1, 27–36, https://doi.org/10.1016/j.cam.2008.10.018, MR2522496, ZBL1170.15005.
10.1016/j.cam.2008.10.018
Web of Science® Google Scholar
23 Duan X., Li C., and Liao A., Solutions and perturbation analsis for the nonlinear matrix equation , Applied Mathematics and Computation. (2011) 218, no. 8, 4458–4466, https://doi.org/10.1016/j.amc.2011.10.026, MR2862116.
10.1016/j.amc.2011.10.026
Google Scholar
24 Duan X. and Liao A., On the existence of Hermitian positive definite solutions of the matrix equation X^s + A^* X^−tA = Q, Linear Algebra and its Applications. (2008) 429, no. 4, 673–687, https://doi.org/10.1016/j.laa.2008.03.019, MR2428122, ZBL1143.15011.
10.1016/j.laa.2008.03.019
Web of Science® Google Scholar
25 Dehghan M. and Hajarian M., Finite iterative algorithms for the reflexive and anti-reflexive solutions of the matrix equation A₁X₁B₁ + A₂X₂B₂ = C, Mathematical and Computer Modelling. (2009) 49, no. 9-10, 1937–1959, https://doi.org/10.1016/j.mcm.2008.12.014, MR2532100, ZBL1171.15310.
10.1016/j.mcm.2008.12.014
Web of Science® Google Scholar
26 Dehghan M. and Hajarian M., Two iterative algorithms for solving coupled matrix equations over reflexive and anti-reflexive matrices, Computational & Applied Mathematics. (2012) 31, no. 2, 353–371, https://doi.org/10.1590/S1807-03022012000200008, MR2991771, ZBL1262.65054.
10.1590/S1807-03022012000200008
Web of Science® Google Scholar
27 Dehghan M. and Hajarian M., Analysis of an iterative algorithm to solve the generalized coupled Sylvester matrix equations, Applied Mathematical Modelling. (2011) 35, no. 7, 3285–3300, https://doi.org/10.1016/j.apm.2011.01.022, MR2785279, ZBL1227.65037.
10.1016/j.apm.2011.01.022
Web of Science® Google Scholar
28 Hajarian M. and Dehghan M., The generalized centro-symmetric and least squares generalized centro-symmetric solutions of the matrix equation AYB + CY^TD = E, Mathematical Methods in the Applied Sciences. (2011) 34, no. 13, 1562–1579, https://doi.org/10.1002/mma.1459, MR2850542, ZBL1228.65066.
10.1002/mma.1459
Web of Science® Google Scholar
29 Dehghan M. and Hajarian M., The general coupled matrix equations over generalized bisymmetric matrices, Linear Algebra and its Applications. (2010) 432, no. 6, 1531–1552, https://doi.org/10.1016/j.laa.2009.11.014, MR2580446, ZBL1187.65042.
10.1016/j.laa.2009.11.014
Web of Science® Google Scholar
30 Dehghan M. and Hajarian M., An iterative method for solving the generalized coupled Sylvester matrix equations over generalized bisymmetric matrices, Applied Mathematical Modelling. Simulation and Computation for Engineering and Environmental Systems. (2010) 34, no. 3, 639–654, https://doi.org/10.1016/j.apm.2009.06.018, MR2563346, ZBL1185.65054.
10.1016/j.apm.2009.06.018
Google Scholar
31 Wu A.-G., Zeng X., Duan G.-R., and Wu W.-J., Iterative solutions to the extended Sylvester-conjugate matrix equations, Applied Mathematics and Computation. (2010) 217, no. 1, 130–142, https://doi.org/10.1016/j.amc.2010.05.029, MR2672571, ZBL1223.65032.
10.1016/j.amc.2010.05.029
Web of Science® Google Scholar
32 Wu A.-G., Feng G., Duan G.-R., and Wu W.-J., Iterative solutions to coupled Sylvester-conjugate matrix equations, Computers & Mathematics with Applications. (2010) 60, no. 1, 54–66, https://doi.org/10.1016/j.camwa.2010.04.029, MR2651883, ZBL1198.65083.
10.1016/j.camwa.2010.04.029
Web of Science® Google Scholar
33 Wu A.-G., Li B., Zhang Y., and Duan G.-R., Finite iterative solutions to coupled Sylvester-conjugate matrix equations, Applied Mathematical Modelling. (2011) 35, no. 3, 1065–1080, https://doi.org/10.1016/j.apm.2010.07.053, MR2740850, ZBL1211.15024.
10.1016/j.apm.2010.07.053
Web of Science® Google Scholar
34 Wu A.-G., Lv L., and Hou M.-Z., Finite iterative algorithms for a common solution to a group of complex matrix equations, Applied Mathematics and Computation. (2011) 218, no. 4, 1191–1202, https://doi.org/10.1016/j.amc.2011.05.096, MR2831627, ZBL1229.65071.
10.1016/j.amc.2011.05.096
Web of Science® Google Scholar
35 Wu A.-G., Lv L., and Hou M.-Z., Finite iterative algorithms for extended Sylvester-conjugate matrix equations, Mathematical and Computer Modelling. (2011) 54, no. 9-10, 2363–2384, https://doi.org/10.1016/j.mcm.2011.05.045, MR2834638, ZBL1235.65040.
10.1016/j.mcm.2011.05.045
Google Scholar
36 Wang M., Wei M., and Feng Y., An iterative algorithm for least squares problem in quaternionic quantum theory, Computer Physics Communications. (2008) 179, no. 4, 203–207, https://doi.org/10.1016/j.cpc.2008.02.016, MR2585244, ZBL1197.81138.
10.1016/j.cpc.2008.02.016
CAS Web of Science® Google Scholar
37 Zhang F., Quaternions and matrices of quaternions, Linear Algebra and its Applications. (1997) 251, 21–57, https://doi.org/10.1016/0024-3795(95)00543-9, MR1421264, ZBL0873.15008.
10.1016/0024-3795(95)00543-9
Web of Science® Google Scholar
38 Le Bihan N. and Mars J., Singular value decomposition of quaternion matrices: a new tool for vector-sensor signal processing, Signal Processing. (2004) 84, no. 7, 1177–1199, 2-s2.0-2642566022, https://doi.org/10.1016/j.sigpro.2004.04.001.
10.1016/j.sigpro.2004.04.001
Web of Science® Google Scholar
39 Farid F. O., Wang Q.-W., and Zhang F., On the eigenvalues of quaternion matrices, Linear and Multilinear Algebra. (2011) 59, no. 4, 451–473, https://doi.org/10.1080/03081081003739204, MR2802526, ZBL1237.15016.
10.1080/03081081003739204
Web of Science® Google Scholar
40 Took C. C., Mandic D. P., and Zhang F., On the unitary diagonalisation of a special class of quaternion matrices, Applied Mathematics Letters. (2011) 24, no. 11, 1806–1809, https://doi.org/10.1016/j.aml.2011.04.038, MR2812216.
10.1016/j.aml.2011.04.038
Web of Science® Google Scholar
41 Sangwine S. J. and Le Bihan N., Quaternion singular value decomposition based on bidiagonalization to a real or complex matrix using quaternion Householder transformations, Applied Mathematics and Computation. (2006) 182, no. 1, 727–738, https://doi.org/10.1016/j.amc.2006.04.032, MR2292081, ZBL1109.65037.
10.1016/j.amc.2006.04.032
Web of Science® Google Scholar
42 De Leo S. and Scolarici G., Right eigenvalue equation in quaternionic quantum mechanics, Journal of Physics A. (2000) 33, no. 15, 2971–2995, https://doi.org/10.1088/0305-4470/33/15/306, MR1766502, ZBL0954.81008.
10.1088/0305-4470/33/15/306
Google Scholar
43 Wang Q.-W., Liu X., and Yu S.-W., The common bisymmetric nonnegative definite solutions with extreme ranks and inertias to a pair of matrix equations, Applied Mathematics and Computation. (2011) 218, no. 6, 2761–2771, https://doi.org/10.1016/j.amc.2011.08.018, MR2838182, ZBL1267.15017.
10.1016/j.amc.2011.08.018
Google Scholar
44 Wang Q.-W., Zhou Y., and Zhang Q., Ranks of the common solution to six quaternion matrix equations, Acta Mathematicae Applicatae Sinica. (2011) 27, no. 3, 443–462, https://doi.org/10.1007/s10255-011-0083-9, MR2810515.
10.1007/s10255-011-0083-9
CAS Google Scholar
45 Wang Q.-W., Chang H.-X., and Lin C.-Y., P-(skew)symmetric common solutions to a pair of quaternion matrix equations, Applied Mathematics and Computation. (2008) 195, no. 2, 721–732, https://doi.org/10.1016/j.amc.2007.05.021, MR2381251, ZBL1149.15011.
10.1016/j.amc.2007.05.021
Web of Science® Google Scholar
46 Wang Q.-W., van der Woude J. W., and Chang H.-X., A system of real quaternion matrix equations with applications, Linear Algebra and its Applications. (2009) 431, no. 12, 2291–2303, https://doi.org/10.1016/j.laa.2009.02.010, MR2563022, ZBL1180.15019.
10.1016/j.laa.2009.02.010
Web of Science® Google Scholar
47 Wang Q., Yu S., and Xie W., Extreme ranks of real matrices in solution of the quaternion matrix equation AXB = C with applications, Algebra Colloquium. (2010) 17, no. 2, 345–360, MR2654356, ZBL1188.15016.
10.1142/S1005386710000349
Web of Science® Google Scholar
48 Fletcher L. R., Kautsky J., and Nichols N. K., Eigenstructure assignment in descriptor systems, IEEE Transactions on Automatic Control. (1986) AC-31, no. 12, 1138–1141, 2-s2.0-0022863919.
10.1109/TAC.1986.1104189
Web of Science® Google Scholar
49 Dai L., Singular Control Systems, 1989, 118, Springer, Berlin, Germany, Lecture Notes in Control and Information Sciences, https://doi.org/10.1007/BFb0002475, MR986970.
10.1007/BFb0002475
Web of Science® Google Scholar
50 Frank P. M., Fault diagnosis in dynamic systems using analytical and knowledge-based redundancy: a survey and some new results, Automatica. (1990) 26, no. 3, 459–474, 2-s2.0-0025421966, https://doi.org/10.1016/0005-1098(90)90018-D.
10.1016/0005-1098(90)90018-D
Web of Science® Google Scholar
51 Peng Y.-X., Hu X.-Y., and Zhang L., An iteration method for the symmetric solutions and the optimal approximation solution of the matrix equation AXB = C, Applied Mathematics and Computation. (2005) 160, no. 3, 763–777, https://doi.org/10.1016/j.amc.2003.11.030, MR2113117, ZBL1068.65056.
10.1016/j.amc.2003.11.030
Web of Science® Google Scholar
52 Xie L., Liu Y., and Yang H., Gradient based and least squares based iterative algorithms for matrix equations AXB + CX^TD = F, Applied Mathematics and Computation. (2010) 217, no. 5, 2191–2199, https://doi.org/10.1016/j.amc.2010.07.019, MR2727965, ZBL1210.65097.
10.1016/j.amc.2010.07.019
Web of Science® Google Scholar
53 Piao F., Zhang Q., and Wang Z., The solution to matrix equation AX + X^TC = B, Journal of the Franklin Institute. (2007) 344, no. 8, 1056–1062, https://doi.org/10.1016/j.jfranklin.2007.05.002, MR2389931, ZBL1171.15015.
10.1016/j.jfranklin.2007.05.002
Web of Science® Google Scholar
54 Zhang X. D., Matrix Analysis and Applications, 2004, Tsinghua University Press, Beijing, China.
Google Scholar
55 Horn R. A. and Johnson C. R., Topics in Matrix Analysis, 1991, Cambridge University Press, Cambridge, UK, https://doi.org/10.1017/CBO9780511840371, MR1091716.
10.1017/CBO9780511840371
Google Scholar

Citing Literature

All articles

Iterative Algorithm for Solving a Class of Quaternion Matrix Equation over the Generalized (P, Q)-Reflexive Matrices

Abstract

1. Introduction and Notations

2. Preliminaries

3. An Iterative Algorithm for Solving Problem 1

4. The Solution of Problem 2

5. Examples

6. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Iterative Algorithm for Solving a Class of Quaternion Matrix Equation over the Generalized (P, Q)-Reflexive Matrices

Abstract

1. Introduction and Notations

2. Preliminaries

3. An Iterative Algorithm for Solving Problem 1

4. The Solution of Problem 2

5. Examples

6. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information