Volume 2013, Issue 1 823098

Research Article

Open Access

A Collocation Method Based on the Bernoulli Operational Matrix for Solving High-Order Linear Complex Differential Equations in a Rectangular Domain

Faezeh Toutounian

Department of Applied Mathematics, School of Mathematical Sciences, Ferdowsi University of Mashhad, Mashhad, Iran um.ac.ir

Center of Excellence on Modelling and Control Systems, Ferdowsi University of Mashhad, Mashhad, Iran

Search for more papers by this author

Emran Tohidi,

Emran Tohidi

orcid.org/0000-0001-7211-5307

Department of Applied Mathematics, School of Mathematical Sciences, Ferdowsi University of Mashhad, Mashhad, Iran um.ac.ir

Search for more papers by this author

Stanford Shateyi,

Corresponding Author

Stanford Shateyi

[email protected]

orcid.org/0000-0002-5829-8634

Department of Mathematics, University of Venda, Private Bag X5050, Thohoyandou 0950, South Africa univen.ac.za

Search for more papers by this author

Faezeh Toutounian,

Faezeh Toutounian

Department of Applied Mathematics, School of Mathematical Sciences, Ferdowsi University of Mashhad, Mashhad, Iran um.ac.ir

Center of Excellence on Modelling and Control Systems, Ferdowsi University of Mashhad, Mashhad, Iran

Search for more papers by this author

Emran Tohidi,

Emran Tohidi

orcid.org/0000-0001-7211-5307

Department of Applied Mathematics, School of Mathematical Sciences, Ferdowsi University of Mashhad, Mashhad, Iran um.ac.ir

Search for more papers by this author

Stanford Shateyi,

Corresponding Author

Stanford Shateyi

[email protected]

orcid.org/0000-0002-5829-8634

Department of Mathematics, University of Venda, Private Bag X5050, Thohoyandou 0950, South Africa univen.ac.za

Search for more papers by this author

First published: 08 April 2013

https://doi.org/10.1155/2013/823098

Citations: 25

Academic Editor: Douglas Anderson

Share a link

Email
Wechat
Bluesky

Abstract

This paper contributes a new matrix method for the solution of high-order linear complex differential equations with variable coefficients in rectangular domains under the considered initial conditions. On the basis of the presented approach, the matrix forms of the Bernoulli polynomials and their derivatives are constructed, and then by substituting the collocation points into the matrix forms, the fundamental matrix equation is formed. This matrix equation corresponds to a system of linear algebraic equations. By solving this system, the unknown Bernoulli coefficients are determined and thus the approximate solutions are obtained. Also, an error analysis based on the use of the Bernoulli polynomials is provided under several mild conditions. To illustrate the efficiency of our method, some numerical examples are given.

1. Introduction

Complex differential equations have a great popularity in science and engineering. In real world, physical events can be modeled by complex differential equations usually. For instance, the vibrations of a one-mass system with two DOFs are mostly described using differential equations with a complex dependent variable [1, 2]. The various applications of differential equations with complex dependent variables are introduced in [2]. Since a huge size of such equations cannot be solved explicitly, it is often necessary to resort to approximation and numerical techniques.

In recent years, the studies on complex differential equations, such as a geometric approach based on meromorphic function in arbitrary domains [3], a topological description of solutions of some complex differential equations with multivalued coefficients [4], the zero distribution [5], growth estimates [6] of linear complex differential equations, and also the rational together with the polynomial approximations of analytic functions in the complex plane [7, 8], were developed very rapidly and intensively.

Since the beginning of 1994, the Laguerre, Chebyshev, Taylor, Legendre, Hermite, and Bessel (matrix and collocation) methods have been used in the works in [9–19] to solve linear differential, integral, and integrodifferential-difference equations and their systems. Also, the Bernoulli matrix method has been used to find the approximate solutions of differential and integrodifferential equations [20–22].

In this paper, in the light of the above-mentioned methods and by means of the matrix relations between the Bernoulli polynomials and their derivatives, we develop a new method called the Bernoulli collocation method (BCM) for solving high-order linear complex differential equation

()

with the initial conditions

()

Evidently, we will let z denote a variable point in the complex plane. Its real and imaginary parts will be denoted by x and y, respectively.

Here, the coefficients P_k(z) and the known function G(z) together with the unknown function f(z) are holomorphic (or analytic) functions in the domain D = {z ∈ ℂ : z = x + iy, a ≤ x ≤ b, c ≤ y ≤ d : a, b, c, d ∈ ℝ} where the coefficients β_r are appropriate complex constants.

We assume that the solution of (1) under the conditions (2) is approximated in the form

()

which is the truncated Bernoulli series of the unknown function f(z), where all of f_n (n = 0,1, …, N) are the Bernoulli coefficients to be determined. We also use the collocation points

()

In this paper, by generalizing the methods [20, 21] from real calculus to the complex calculus, we propose a new matrix method which is based on the Bernoulli operational matrix of differentiation and a uniform collocation scheme. It should be noted that since an ordinary complex differential equation equals to a system of partial differential equations (see Section 4) the methods that based on high-order Gauss quadrature rules [23, 24] could not be effective. Needing to more CPU time from one side and ill conditioning of the associated algebraic problem from another side are two disadvantages of such methods. Therefore, implementing an easy to use approach such as the methods that based on operational matrices is necessary for solving any practical problem.

The rest of this paper is organized as follows. In Section 2, we review some notations from complex calculus and also provide several properties of the Bernoulli polynomials. Section 3 is devoted to the proposed matrix method. Error analysis and accuracy of the approximated solution by the aid of the Bernoulli polynomials is given in Section 4. Several illustrative examples are provided in Section 5 for confirming the effectiveness of the presented method. Section 6 contains some conclusions and notations about the future works.

2. Review on Complex Calculus and the Bernoulli Polynomials

This Section is divided into two subsections. In the first subsection we review some notations from complex calculus specially the concept of differentiability in the complex plane under some remarks. Then we recall several properties of the Bernoulli polynomials and introduce the operational matrix of differentiation of the Bernoulli polynomials in the complex form.

2.1. Review on Complex Calculus

From the definition of derivative in the complex form, it is immediate that a constant function is differentiable everywhere, with derivative 0, and that the identity function (the function f(z) = z) is differentiable everywhere, with derivative 1. Just as in elementary calculus one can show from the last statement, by repeated applications of the product rule, that, for any positive integer n, the function f(z) = zⁿ is differentiable everywhere, with derivative nzⁿ⁻¹. This, in conjunction with the sum and product rules, implies that every polynomial is everywhere differentiable: if f(z) = c_nzⁿ + c_n−1zⁿ⁻¹ + ⋯+c₁z + c₀, where c₀, …, c_n are complex constants, then f^′(z) = nc_nzⁿ⁻¹ + (n − 1)c_n−1zⁿ⁻² + ⋯+c₁.

Remark 1. The function f = u + iv is differentiable (in the complex sense) at z₀ if and only if u and v are differentiable (in the real sense) at z₀ and their first partial derivatives satisfy the relations ∂u(z₀)/∂x = ∂v(z₀)/∂y, ∂u(z₀)/∂y = −∂v(z₀)/∂x. In that case

()

Remark 2. Two partial differential equations

()

are called the Cauchy-Riemann equations for the pair of functions u, v. As seen above (i.e., the Remark 1), the equations are satisfied by the real and imaginary parts of a complex-valued function at each point where that function is differentiable.

Remark 3 (sufficient condition for complex differentiability). Let the complex-valued function f = u + iv be defined in the open subset G of the complex plane ℂ and assume that u and v have first partial derivatives in G. Then f is differentiable at each point where those partial derivatives are continuous and satisfy the Cauchy-Riemann equations.

Definition 4. A complex-valued function that is defined in an open subset G of the complex plane ℂ and differentiable at every point of G is said to be holomorphic (or analytic) in G. The simplest examples are polynomials, which are holomorphic in ℂ, and rational functions, which are holomorphic in the regions where they are defined. Moreover, the elementary functions such as exponential function, the logarithm function, trigonometric and inverse trigonometric functions, and power functions all have complex versions that are holomorphic functions. It should be noted that if the real and imaginary parts of a complex-valued function have continuous first partial derivatives obeying the Cauchy-Riemann equations, then the function is holomorphic.

Remark 5 (complex partial differential operators). The partial differential operators ∂/∂x and ∂/∂y are applied to a complex-valued function f = u + iv in the natural way:

()

We define the complex partial differential operators ∂/∂z and

()

Thus,

Intuitively one can think of a holomorphic function as a complex-valued function in an open subset of ℂ that depends only on z, that is, independent of . We can make this notion precisely as follows. Suppose the function f = u + iv is defined and differentiable in an open set. One then has

()

The Cauchy-Riemann equations thus can be written

. As this is the condition for f to be holomorphic, it provides a precise meaning for the statement: a holomorphic function is one that is independent of

. If f is holomorphic, then (not surprisingly) f^′ = ∂f/∂z, as the following calculation shows:

()

2.2. The Bernoulli Polynomials and Their Operational Matrix

The Bernoulli polynomials play an important role in different areas of mathematics, including number theory and the theory of finite differences. The classical Bernoulli polynomials B_n(x) are usually defined by means of the exponential generating functions (see [21])

()

The following familiar expansion (see [20]):

()

is the most primary property of the Bernoulli polynomials. The first few Bernoulli polynomials are

()

The Bernoulli polynomials satisfy the well-known relations (see [21])

()

The Bernoulli polynomials have another specific property that is satisfied in the following linear homogeneous recurrence relation [20]:

()

Also, the Bernoulli polynomials satisfy the following interesting property [25]:

()

Moreover, B_n(x) satisfy the differential equation [20]

()

According to the discussions in [20], the Bernoulli polynomials form a complete basis over the interval [0, 1].

If we introduce the Bernoulli vector B(x) in the form B(x) = [B₀(x), B₁(x), …, B_N(x)], then the derivative of B(x), with the aid of the first property of (14), can be expressed in the matrix form by

()

where M is the (N + 1)×(N + 1) operational matrix of differentiation. Note that if we replace the real variable x by the complex variable z in the above relation, again we reach to the same result, since

Accordingly, the kth derivative of B(x) can be given by

()

where M is defined in (18).

We recall that the Bernoulli expansions and Taylor series are not based on orthogonal functions; nevertheless, they possess the operational matrices of differentiations (and also integration). However, since the integration of the cross product of two Taylor series vectors is given in terms of a Hilbert matrix, which are known to be ill conditioned, the applications of Taylor series in the integration form of view are limited. But in differential form of view, (see for instance [10–12, 16, 17] and the references therein) use the operational matrix of derivatives such as Taylor in a huge number of research works. For approximating an arbitrary unknown function, the advantages of the Bernoulli polynomials over orthogonal polynomials as shifted Legendre polynomials are the following.

(i)
The operational matrix of differentiation in the Bernoulli polynomials has less nonzero elements than for shifted Legendre polynomials. Because for Bernoulli polynomials, the nonzero elements of this matrix are located in below (or above) its diagonal. However for the shifted Legendre polynomials is a strictly lower (or upper) filled triangular matrix.
(ii)
The Bernoulli polynomials have less terms than shifted Legendre polynomials. For example, B₆(x) (the 6th Bernoulli polynomial) has 5 terms while P₆(x) (the 6th shifted Legendre polynomial) has 7 terms, and this difference will increase by increasing the index. Hence, for approximating an arbitrary function we use less CPU time by applying the Bernoulli polynomials as compared to shifted Legendre polynomials; this issue is claimed in [25] and is proved in its examples for solving nonlinear optimal control problems.
(iii)
The coefficient of individual terms in the Bernoulli polynomials is smaller than the coefficient of individual terms in the shifted Legendre polynomials. Since the computational errors in the product are related to the coefficients of individual terms, the computational errors are less by using the Bernoulli polynomials.

3. Basic Idea

In this section by applying the Bernoulli operational matrix of differentiation and also the collocation scheme, the basic idea of this paper would be constructed. We again consider (1) and its approximated solution f_N(z) in the form (3). Trivially, f_N(z) could be rewritten in the vector form

()

By using (19) in the complex form one can conclude that

()

where M is introduced in (19).

For the collocation points z = z_pp (p = 0,1, …, N), the matrix relation (21) becomes

()

where B(z_pp) = [B₀(z_pp) B₁(z_pp) ⋯ B_N(z_pp)]. For more details, one can restate (22) as follows:

()

The matrix vector of the above-mentioned equations is

()

where

()

On the other hand by substituting the collocation points z = z_pp defined by (4) into (1), we have

()

The associated matrix-vector form of the above equations has the following form by the aid of (24):

()

where

()

Since the vector F is unknown and should be determined, therefore, the matrix-vector equation (27) could be rewritten in the following form:

()

where

We now write the vector form of the initial conditions (2) by the aid of (21) as follows:

()

In other words the vector form of the initial conditions could be rewritten as U_rF = β_r where

(r = 0,1, …, m − 1). Trivially the augmented form of these equations is

()

Consequently, to find the unknown Bernoulli coefficients f_n, n = 0,1, …, N, related with the approximate solution of the problem (1) under the initial conditions (2), we need to replace the m rows of (31) by the last m rows of the augmented matrix (29) and hence we have new augmented matrix

()

or the corresponding matrix-vector equation

()

one can rewrite (32) in the form

and the vector F is uniquely determined. Thus the mth order linear complex differential equation with variable coefficients (1) under the conditions (2) has an approximated solution. This solution is given by the truncated Bernoulli series (3). Also we can easily check the accuracy of the obtained solutions as follows [12, 26]. Since the truncated Bernoulli series (3) is an approximate solution of (1), when the solutions f(z) and its derivatives are substituted in (1), the resulting equation must be satisfied approximately; that is, for z = z_i ∈ D, i = 0,1, 2, …

()

(k is any positive integer) is prescribed, then the truncation limit N may be increased until the values E(z_i) at each of the points z_i become smaller than the prescribed 10^−k (for more details see [10–12, 16, 17]).

4. Error Analysis and Accuracy of the Solution

This section is devoted to provide an error bound for the approximated solution which may be obtained by the Bernoulli polynomials. We emphasized that this section is given for showing the efficiency of the Bernoulli polynomial approximation and is independent of the proposed method which is provided for showing how a complex ordinary differential equation (ODE) is equivalent to a system of partial differential equations (PDEs). After conveying this subject, we transform the obtained system of PDEs (together with the initial conditions (2)) to a system of two dimensional Volterra integral equations in a special case. Before presenting the main Theorem of this section, we need to recall some useful corollaries and lemmas. Therefore, the main theorem could be stated which guarantees the convergence of the truncated Bernoulli series to the exact solution under several mild conditions.

Now suppose that H = L²[0,1] and {B₀(x), B₁(x), …, B_N(x)} ⊂ H be the set of the Bernoulli polynomials and

()

and g be an arbitrary element in H. Since Y is a finite dimensional vector space, g has the unique best approximation

, such that

()

Since

, there exists the unique coefficients g₀, g₁, …, g_N such that

()

Corollary 6. Assume that g ∈ H = L²[0,1] be an enough smooth function and also is approximated by the Bernoulli serie , then the coefficients g_n for all n = 0,1, …, ∞ can be calculated from the following relation:

()

Proof. See [21].

In practice one can use finite terms of the above series. Under the assumptions of Corollary 6, we will provide the error of the associated approximation.

Lemma 7 (see [20].)Suppose that g(x) be an enough smooth function in the interval and be approximated by the Bernoulli polynomials as done in Corollary 6. With more details assume that P_N[g](x) is the approximate polynomial of g(x) in terms of the Bernoulli polynomials and R_N[g](x) is the remainder term. Then, the associated formulas are stated as follows:

()

where

and [x] denotes the largest integer not greater than x.

Proof. See [20].

Lemma 8. Suppose g(x) ∈ C^∞[0,1] (with bounded derivatives) and g_N(x) is the approximated polynomial using Bernoulli polynomials. Then the error bound would be obtained as follows:

()

where

denotes a bound for all the derivatives of function g(x) (i.e.,

, for i = 0,1, …) and C is a positive constant.

Proof. By using Lemma 7, we have

()

According to [20] one can write

()

Now we use the formulae (1.1.5) in [27] for the even Bernoulli numbers as follows:

()

Therefore,

()

In other words , where C is a positive constant independent of N. This completes the proof.

Corollary 9. Assume that u(x, y) ∈ H × H = L²[0,1] × L²[0,1] be an enough smooth function and also is approximated by the two variable Bernoulli series , then the coefficients u_m,n for all m, n = 0,1, …, ∞ can be calculated from the following relation:

()

Proof. By applying a similar procedure in two variables (which was provided in Corollary 6) we can conclude the desired result.

In [28], a generalization of Lemma 7 can be found. Therefore, we just recall the error of the associated approximation in two dimensional functions.

Lemma 10. Suppose that u(x, y) be an enough smooth function and u_N(x, y) be the approximated polynomial of u(x, y) in terms of linear combination of Bernoulli polynomials by the aid of Corollary 9. Then the error bound would be obtained as follows:

()

where

is a positive constant independent of N and is a bound for all the partial derivatives of u(x, y).

We now consider the basic equation (1) together with the initial conditions (2). For clarity of presentation we assume that m = 1, P(z) = P₀(z), and β = β₀. A similar procedure would be applied in the case of larger values of m. Equation (1) with the above-mentioned assumptions has the following form:

()

where

()

Also the initial condition f(0) = u(0,0) + iv(0,0) = β = β₁ + iβ₂ should be considered. Thus, one can write u(0,0) = β₁ and v(0,0) = β₂.

According to Remark 5, since f(z) is a Holomorphic function, then (47) by using assumptions in (48) could be rewritten as follows:

()

In other words

()

For imposing the initial conditions u(0,0) = β₁ and v(0,0) = β₂, we need to differentiate the above equations with respect to y and then integrate with respect to x and y in the rectangular [0, x] × [0, y]. Therefore, by differentiating both of the equations of (50) with respect to y we have

()

Integrating from the above equations in the rectangular [0, x] × [0, y] yields

()

By imposing the the initial conditions u(0,0) = β₁ and v(0,0) = β₂ to these equations we reach to

()

where

()

Considering

and

, (53) could be restated in the following matrix vector form:

()

Our aim is to show that lim _N→∞ U_N(x, y) = U(x, y) or lim _N→∞ f_N(z) = f(z), where

, f_N(z) = u_N(x, y) + iv_N(x, y) and f_N(z) was introduced in (3).

In the following lines, the main theorem of this section would be provided. However, some mild conditions should be assumed. These conditions are as follows:

(i)
,
(ii)
.

It should be noted that the second condition is based upon Lemmas 8 and 10.

Theorem 11. Assume that U and U₀ : = U(x, 0) be approximated by U_N and U_0,N, respectively, by the aid of the Bernoulli polynomials in (55) and also we use a collocation scheme for providing the numerical solution of (55). In other words

()

where R_N+1(x, y) is the residual function that is zero at the (N + 1) collocation nodes. Also suppose that [a, b] = [c, d] = [0,1]. Then, under the above-mentioned assumptions

()

and lim _N→∞ U_N(x, y) = U(x, y).

Proof. By subtracting (56) from (55) we have

()

Therefore,

()

Since , we have ; in other words, lim _N→∞ f_N(z) = f(z) and this completes the proof.

5. Numerical Examples

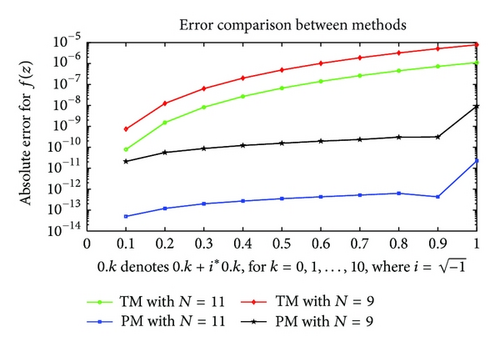
In this section, several numerical examples are given to illustrate the accuracy and effectiveness of the proposed method and all of them are performed on a computer using programs written in MATLAB 7.12.0 (v2011a) (The Mathworks Inc., Natick, MA, USA). In this regard, we have reported in the tables and figures the values of the exact solution f(z), the polynomial approximate solution f_N(z), and the absolute error function e_N(z) = |f(z) − f_N(z)| at the selected points of the given domains. It should be noted that in the first example we consider a complex differential equation with an exact polynomial solution. Our method obtains such exact polynomial solutions readily by solving the associated linear algebraic system.

Example 12 (see [26].)As the first example, we consider the first-order complex differential equation with variable coefficients

()

with the initial condition f(0) = −1 and the exact solution 2z − 1. We suppose that N = 3. Therefore, the collocation points are z₀₀ = 0, z₁₁ = (1 + i)/3, z₂₂ = (2 + 2i)/3, and z₃₃ = 1 + i. According to (3), the approximate solution has the following form:

()

where our aim is to find the unknown Bernoulli coefficients f₀, f₁, f₂, and f₃. Since P₀(z) = z, then

()

Also the matrix L (with the assumption N = 3) has the following structure:

()

where B₀(z) = 1, B₁(z) = z − 1/2, B₂(z) = z² − z + 1/6 and B₃(z) = z³ − (3/2)z² + z/2.

According to (29), the matrix coefficients W are as follows:

()

Since G(z) = 2z² − z + 2, the right-hand side vector G has the following form:

()

The associated form of the initial condition f(0) = −1 is

()

Imposing the above initial condition to the matrix W and vector G yields

()

Therefore, the solution of the system

is as follows:

()

Thus, we obtain the approximate solution f₃(z) = B(z)F = 2z − 1 which is the exact solution. We recall that

()

Example 13 (see [26].)As the second example, we consider the following second-order complex differential equation

()

with the initial conditions f(0) = f^′(0) = 1 and the exact solution f(z) = exp (z). In this equation, we have P₀(z) = P₁(z) = z and G(z) = exp (z) + 2z exp (z). Then, for N = 5 the collocation points are z₀₀ = 0, z₁₁ = (1 + i)/5, z₂₂ = (2 + 2i)/5, z₃₃ = (3 + 3i)/5, z₄₄ = (4 + 4i)/5, and z₅₅ = 1 + i.

According to (29), the fundamental matrix equation is

()

where M^T and L are introduced in (18) and (25), respectively. Also

()

The right-hand side vector G is

()

The augmented matrix forms of the initial conditions for N = 5 are

()

By replacing the above augmented vectors to the last two rows of [W; G], we reach to

. The solution of the matrix-vector equation

()

We also solve this equation by assumptions N = 7 and N = 9. Since the exact solution of the equation is exp (z) = exp (x + iy) = exp (x)(cos (y) + isin (y)). Therefore, the real and imaginary parts of the exact solution are Re(exp (z)) = exp (x)cos (y) and Im (exp (z)) = exp (x)sin (y), respectively. The values of the approximate solution in the case of N = 5,7, and 9 for both parts of real and imaginary together with the exact solution are provided in Tables 1 and 2. Also an interesting comparison between the presented method (PM) and the Taylor method [26] (TM) has been provided in Figure 1 for N = 7 and 9. From this figure, one can see the efficiency of our methods with respect to the method of [26].

Table 1. Numerical results of Example 13, for Re(exp (z)) = exp (x)cos (y).

z = x + iy	Exact solution (real)	PM for N = 5	PM for N = 7	PM for N = 9
0.0 + 0.0i	1.000000000000000	1.000000000000002	0.999999999999999	1.000000000000002
0.1 + 0.1i	1.099649666829409	1.099650127059032	1.099649681790901	1.099649666809790
0.2 + 0.2i	1.197056021355891	1.197058065414137	1.197056071303251	1.197056021305326
0.3 + 0.3i	1.289569374044936	1.289572683703872	1.289569451705194	1.289569373971185
0.4 + 0.4i	1.374061538887522	1.374064757066184	1.374061646628469	1.374061538795035
0.5 + 0.5i	1.446889036584169	1.446891795476775	1.446889179088898	1.446889036484456
0.6 + 0.6i	1.503859540558786	1.503862872087464	1.503859710928599	1.503859540462517
0.7 + 0.7i	1.540203025431780	1.540203451564549	1.540203240474244	1.540203025363573
0.8 + 0.8i	1.550549296807422	1.550520218427163	1.550549536105736	1.550549296761452
0.9 + 0.9i	1.528913811884699	1.528765905385641	1.528913283429636	1.528913812578978
1.0 + 1.0i	1.468693939915885	1.468204121679876	1.468688423751699	1.468693951050675

Table 2. Numerical results of Example 13, for Im (exp (z) = exp (z)sin(y).

z = x + iy	Exact solution (Im)	PM for N = 5	PM for N = 7	PM for N = 9
0.0 + i0.0	0	0.000000000000000	−0.000000000000001	0.000000000000000
0.1 + i0.1	0.110332988730204	0.110330942667805	0.110332993217700	0.110332988786893
0.2 + i0.2	0.242655268594923	0.242645839814175	0.242655282953655	0.242655268747208
0.3 + i0.3	0.398910553778490	0.398893389645474	0.398910574081883	0.398910554017485
0.4 + i0.4	0.580943900770567	0.580922057122650	0.580943925558894	0.580943901105221
0.5 + i0.5	0.790439083213615	0.790412124917929	0.790439110267023	0.790439083643388
0.6 + i0.6	1.028845666272092	1.028807744371502	1.028845687924972	1.028845666809275
0.7 + i0.7	1.297295111875269	1.297248986448220	1.297295129424920	1.297295112510736
0.8 + i0.8	1.596505340600251	1.596503892694281	1.596505330955563	1.596505341401562
0.9 + i0.9	1.926673303972717	1.926900526193919	1.926672856270450	1.926673303646987
1.0 + i1.0	2.287355287178843	2.288259022526098	2.287352245460983	2.287355267120311

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Comparisons of the presented method (PM) and the Taylor method (TM) of Example 13.

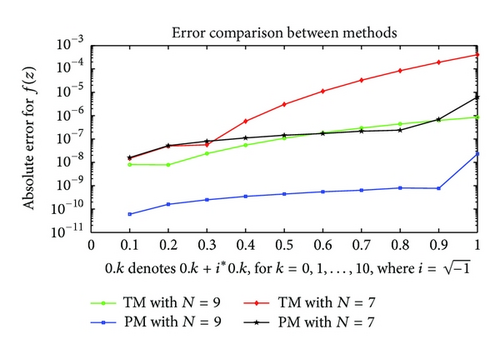
Example 14 (see [26].)As the final example, we consider the following second-order complex differential equation

()

with the initial conditions f(0) = 0 and f^′(0) = 1 and also the exact solution f(z) = sin(z). In this equation, we have P₀(z) = 2z, P₁(z) = z, and G(z) = 2zsin (z) + zcos (z) − sin (z). Similar to the previous two examples, we solve this equation in the case of N = 9 and 11. In Figure 2, we provide a comparison between our method and the Taylor method (TM) [26]. According to this figure, one can see that not only our method is superior in results but also the behaviour of the error of the presented method has a stable manner with respect to the Taylor method [26] during the computational interval. Moreover, since the Bessel method and the presented method can be considered as an preconditioned solution of any linear algebraic system which is originated from the above differential equation, they have the same accuracy. But the condition number of the matrix coefficients

of the Bessel method is very larger than the matrix coefficient

of our method. This subject is illustrated in Figure 3. It should be noted that this figure is depicted according to the diagonal collocation methods and the square collocation method was not used.

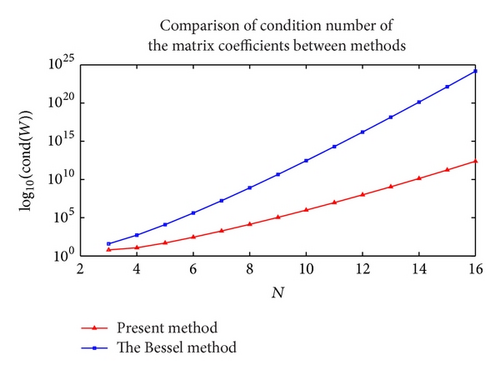
6. Conclusions

High-order linear complex differential equations are usually difficult to solve analytically. Then, it is required to obtain the approximate solutions. For this reason, a new technique using the Bernoulli polynomials to numerically solve such equations is proposed. This method is based on computing the coefficients in the Bernoulli series expansion of the solution of a linear complex differential equation and is valid when the functions P_k(z) and G(z) are defined in the rectangular domain. An interesting feature of this method is to find the analytical solutions if the equation has an exact solution that is a polynomial of degree N or less than N. Shorter computation time and lower operation count results in reduction of cumulative truncation errors and improvement of overall accuracy are some of the advantages of our method. In addition, the method can also be extended to the system of linear complex equations with variable coefficients, but some modifications are required.

Conflict of Interests

The authors declare that they do not have any conflict of interests in their submitted paper.

Acknowledgments

The authors thank the Editor and both of the reviewers for their constructive comments and suggestions to improve the quality of the paper.

References

1 Cveticanin L., Free vibration of a strong non-linear system described with complex functions, Journal of Sound and Vibration. (2004) 277, no. 4-5, 815–824, https://doi.org/10.1016/j.jsv.2003.09.032, MR2094264, ZBL1236.70022.
10.1016/j.jsv.2003.09.032
Web of Science® Google Scholar
2 Cveticanin L., Approximate solution of a strongly nonlinear complex differential equation, Journal of Sound and Vibration. (2005) 284, no. 1-2, 503–512, https://doi.org/10.1016/j.jsv.2004.08.006, MR2142061, ZBL1237.34058.
10.1016/j.jsv.2004.08.006
Web of Science® Google Scholar
3 Barsegian G. A., Gamma Lines: On the Geometry of Real and Complex Functions, 2002, 5, Taylor & Francis, New York, NY, USA, Asian Mathematics Series, MR2002433.
10.1201/9781482264852
Google Scholar
4 Barsegian G. and Lê D. T., On a topological description of solutions of complex differential equations, Complex Variables. (2005) 50, no. 5, 307–318, https://doi.org/10.1080/02781070500032879, MR2141750, ZBL1082.34076.
10.1080/02781070500032879
Google Scholar
5 Ishizaki K. and Tohge K., On the complex oscillation of some linear differential equations, Journal of Mathematical Analysis and Applications. (1997) 206, no. 2, 503–517, https://doi.org/10.1006/jmaa.1997.5247, MR1433953, ZBL0877.34009.
10.1006/jmaa.1997.5247
Web of Science® Google Scholar
6 Heittokangas J., Korhonen R., and Rättyä J., Growth estimates for solutions of linear complex differential equations, Annales Academiæ Scientiarum Fennicæ. (2004) 29, no. 1, 233–246, MR2041951, ZBL1057.34111.
Google Scholar
7 Andrievskii V., Polynomial approximation of analytic functions on a finite number of continua in the complex plane, Journal of Approximation Theory. (2005) 133, no. 2, 238–244, https://doi.org/10.1016/j.jat.2004.12.016, MR2129480, ZBL1085.30034.
10.1016/j.jat.2004.12.016
Web of Science® Google Scholar
8 Prokhorov V. A., On best rational approximation of analytic functions, Journal of Approximation Theory. (2005) 133, no. 2, 284–296, https://doi.org/10.1016/j.jat.2004.12.007, MR2129484, ZBL1073.30029.
10.1016/j.jat.2004.12.007
Web of Science® Google Scholar
9 Gülsu M. and Sezer M., Approximate solution to linear complex differential equation by a new approximate approach, Applied Mathematics and Computation. (2007) 185, no. 1, 636–645, https://doi.org/10.1016/j.amc.2006.07.050, MR2297834, ZBL1107.65328.
10.1016/j.amc.2006.07.050
Web of Science® Google Scholar
10 Gülsu M., Gürbüz B., Öztürk Y., and Sezer M., Laguerre polynomial approach for solving linear delay difference equations, Applied Mathematics and Computation. (2011) 217, no. 15, 6765–6776, https://doi.org/10.1016/j.amc.2011.01.112, MR2775723, ZBL1211.65166.
10.1016/j.amc.2011.01.112
Web of Science® Google Scholar
11 Öztürk Y. and Gülsu M., Approximate solution of linear generalized pantograph equations with variable coefficients on Chebyshev-Gauss grid, Journal of Advanced Research in Scientific Computing. (2012) 4, no. 1, 36–51, MR2890860.
Google Scholar
12 Sezer M. and Akyuz-Das-cioglu A., A Taylor method for numerical solution of generalized pantograph equations with linear functional argument, Journal of Computational and Applied Mathematics. (2007) 200, no. 1, 217–225, https://doi.org/10.1016/j.cam.2005.12.015, MR2276827, ZBL1112.34063.
10.1016/j.cam.2005.12.015
Web of Science® Google Scholar
13 Sezer M., Gülsu M., and Tanay B., A Taylor collocation method for the numerical solution of complex differential equations with mixed conditions in elliptic domains, Applied Mathematics and Computation. (2006) 182, no. 1, 498–508, https://doi.org/10.1016/j.amc.2006.04.011, MR2292059, ZBL1106.65061.
10.1016/j.amc.2006.04.011
Web of Science® Google Scholar
14 Sezer M. and Yuzbasi S., A collocation method to solve higher order linear complex differential equations in rectangular domains, Numerical Methods for Partial Differential Equations. (2010) 26, no. 3, 596–611, https://doi.org/10.1002/num.20448, MR2656302, ZBL1189.65152.
10.1002/num.20448
Web of Science® Google Scholar
15 Tohidi E., Legendre approximation for solving linear HPDEs and comparison with Taylor and Bernoulli matrix methods, Applied Mathematics. (2012) 3, no. 5, 410–416, https://doi.org/10.4236/am.2012.35063, MR2926642.
10.4236/am.2012.35063
Google Scholar
16 Yuzbasi S., Aynigul M., and Sezer M., A collocation method using Hermite polynomials for approximate solution of pantograph equations, Journal of the Franklin Institute. (2011) 348, no. 6, 1128–1139, https://doi.org/10.1016/j.jfranklin.2011.05.003, MR2803650.
10.1016/j.jfranklin.2011.05.003
Web of Science® Google Scholar
17 Yuzbasi S., A numerical approximation based on the Bessel functions of first kind for solutions of Riccati type differential difference equations, Computers & Mathematics with Applications. (2012) 64, no. 6, 1691–1705, https://doi.org/10.1016/j.camwa.2012.01.026.
10.1016/j.camwa.2012.01.026
Web of Science® Google Scholar
18 Yuzbasi S., Sahin N., and Sezer M., A collocation approach for solving linear complex differential equations in rectangular domains, Mathematical Methods in the Applied Sciences. (2012) 35, no. 10, 1126–1139, https://doi.org/10.1002/mma.1590, MR2945841.
10.1002/mma.1590
Web of Science® Google Scholar
19 Yuzbasi S., Sahin N., and Gulso M., A collocation approach for solving a class of complex differential equations in elliptic domains, Journal of Numerical Mathematics. (2011) 19, no. 3, 225–246, https://doi.org/10.1515/JNUM.2011.011, MR2854138.
10.1515/jnum.2011.011
Web of Science® Google Scholar
20 Bhrawy A. H., Tohidi E., and Soleymani F., A new Bernoulli matrix method for solving high-order linear and nonlinear Fredholm integro-differential equations with piecewise intervals, Applied Mathematics and Computation. (2012) 219, no. 2, 482–497, https://doi.org/10.1016/j.amc.2012.06.020, MR2956980.
10.1016/j.amc.2012.06.020
Web of Science® Google Scholar
21 Tohidi E., Bhrawy A. H., and Erfani Kh., A collocation method based on Bernoulli operational matrix for numerical solution of generalized pantograph equation, Applied Mathematical Modelling. (2013) 37, no. 6, 4283–4294, https://doi.org/10.1016/j.apm.2012.09.032.
10.1016/j.apm.2012.09.032
Web of Science® Google Scholar
22 Tohidi E., Bernoulli matrix approach for solving two dimensional linear hyperbolic partial differential equations with constant coefficients, Journal of Computational and Applied Mathematics. (2012) 2, no. 4, 136–139.
Google Scholar
23 Samadi O. R. N. and Tohidi E., The spectral method for solving systems of Volterra integral equations, Journal of Applied Mathematics and Computing. (2012) 40, no. 1-2, 477–497, https://doi.org/10.1007/s12190-012-0582-8, MR2965344.
10.1007/s12190-012-0582-8
Google Scholar
24 Tohidi E. and Samadi O. R. N., Optimal control of nonlinear Volterra integral equations via Legendre polynomials, IMA Journal of Mathematical Control and Information. (2013) 30, no. 1, 67–83.
10.1093/imamci/dns014
Web of Science® Google Scholar
25 Mashayekhi S., Ordokhani Y., and Razzaghi M., Hybrid functions approach for nonlinear constrained optimal control problems, Communications in Nonlinear Science and Numerical Simulation. (2012) 17, no. 4, 1831–1843, https://doi.org/10.1016/j.cnsns.2011.09.008, MR2855473, ZBL1239.49043.
10.1016/j.cnsns.2011.09.008
Web of Science® Google Scholar
26 Sezer M. and Gülsu M., Approximate solution of complex differential equations for a rectangular domain with Taylor collocation method, Applied Mathematics and Computation. (2006) 177, no. 2, 844–851, https://doi.org/10.1016/j.amc.2005.11.035, MR2292010, ZBL1096.65075.
10.1016/j.amc.2005.11.035
Web of Science® Google Scholar
27 Krylov V. I., Approximate Calculation of Integrals, 1962, Dover, Mineola, NY, USA, MR0144464.
Google Scholar
28 Costabile F. A. and Dell′Accio F., Expansion over a rectangle of real functions in Bernoulli polynomials and applications, BIT Numerical Mathematics. (2001) 41, no. 3, 451–464, https://doi.org/10.1023/A:1021958910686, MR1854267, ZBL0989.65014.
10.1023/A:1021958910686
Google Scholar

Citing Literature

All articles

A Collocation Method Based on the Bernoulli Operational Matrix for Solving High-Order Linear Complex Differential Equations in a Rectangular Domain

Abstract

1. Introduction

2. Review on Complex Calculus and the Bernoulli Polynomials

2.1. Review on Complex Calculus

2.2. The Bernoulli Polynomials and Their Operational Matrix

3. Basic Idea

4. Error Analysis and Accuracy of the Solution

5. Numerical Examples

6. Conclusions

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Collocation Method Based on the Bernoulli Operational Matrix for Solving High-Order Linear Complex Differential Equations in a Rectangular Domain

Abstract

1. Introduction

2. Review on Complex Calculus and the Bernoulli Polynomials

2.1. Review on Complex Calculus

2.2. The Bernoulli Polynomials and Their Operational Matrix

3. Basic Idea

4. Error Analysis and Accuracy of the Solution

5. Numerical Examples

6. Conclusions

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Related

Information