Abstract and Applied Analysis
Volume 2013, Issue 1 813957
Research Article
Open Access

The Application of the Undetermined Fundamental Frequency Method on the Period-Doubling Bifurcation of the 3D Nonlinear System

Gen Ge, 

Corresponding Author

Gen Ge

School of Mechanical Engineering, Tianjin Polytechnic University, Tianjin 300072, China

Search for more papers by this author
Wei Wang, 

Wei Wang

Department of Mechanics, Tianjin University, Tianjin 300072, China tju.edu.cn

Search for more papers by this author
First published: 15 September 2013
https://doi.org/10.1155/2013/813957
Academic Editor: Ren Yong

Abstract

The analytical method to predict the period-doubling bifurcation of the three-dimensional (3D) system is improved by using the undetermined fundamental frequency method. We compute the stable response of the system subject to the quadratic and cubic nonlinearity by introducing the undetermined fundamental frequency. For the occurrence of the first and second period-doubling bifurcation, the new bifurcation criterion is accomplished. It depends on the stability of the limit cycle on the central manifold. The explicit applications show that the new results coincide with the results of the numerical simulation as compared with the initial methods.

1. Introduction

Period-doubling bifurcation can induce complex dynamical behavior in the nonlinear dynamic systems. It is the most classical achievement broadcasted by Feigenbaum [1]. He discovered the ratio of the difference between the values at which such successive period-doubling bifurcation occurs at a constant of around 4.6692 and then showed that the same behavior, with the same mathematical constant, would occur within a wide class of mathematical functions, prior to the onset of chaos. Since then many attempts have been made to study the period-doubling (flip) bifurcation phenomenon in the nonlinear dynamic systems. Wang and Xu [2] developed the relation between two periodic solutions analytically for a general parameter dependent dynamic system. Such relation is further confirmed by one example and shows that the 2T-periodic solution contains all the information of the T-periodic solution near the bifurcation point. From the frequency domain point of view, Floquet multipliers commonly used for the analytical bifurcations of Hopf cycles are the key to detect the appearance of a subharmonic solution. So a quasianalytical monodromy matrix approach was developed to the period-doubling bifurcation emerging near a Hopf bifurcation point [3].

As compared with the single freedom system, the dynamical behaviors surrounding the bifurcation point may become more complicated in the 3D system. Rand [4] used the center manifold theory to approximate the newly born limit cycle and then to investigate the stability of the limit cycle corresponding to the flip bifurcation. Later, Belhaq et al. [5, 6] improved the approximation of the critical value with a higher-order approximation and further solved the problem of the second period-doubling bifurcation.

In this paper, we use the center manifold theory to reduce a 3D system and then derive the critical values of the first and second period-doubling bifurcation according to the stability of the limit cycle. In terms of the undetermined fundamental frequency method, it produces more accurate results and avoids the computational complexity appending the higher-order approximation at the same time [7, 8]. Finally the whole process is precisely programmed in terms of the computer algebra Mathematica to perform the analysis more efficiently.

2. Stable Response with the Undetermined Fundamental Frequency Method

In order to illustrate the analytical process, we refer to the following 3D system:
()

This system may be thought of as a feedback control system consisting of a damped linear oscillator in the x, y variables and a control variable z. The origin (x, y, z) = (0,0, 0) is the equilibrium and may lose its stability at control parameter changing from μ < 0 to μ > 0. This means that the period-doubling bifurcation appears at the value μ = μc following the limit cycles.

For the value of μc, the center manifold theory has to be introduced to finish the reduction and obtain the equations on the center manifolds. So we set the second order polynomial of z in terms of x, y, and μ
()
Differentiating (2) with respect to time t and using (1) give
()
Equating the same order terms on both sides of (3) produces the coefficients
()
That leads to the following approximate flows on the center manifold:
()

The computational precision of the critical value depends heavily on the stable response, such as the frequency and amplitude of the 3D system. So, in order to perform the limit cycle bifurcation analysis more correctly, Belhaq et al. [6] explored the analysis through a higher-order approximation. In this paper we introduce the undetermined fundamental frequency method during the course of normal form operation.

In terms of the transformation x = v − μu, y = u, (5) changes to
()
To obtain the stable response, it demands to transform (6) into a differential equation of the first order with the complex unknown quantities ξ. Let
()
where ω10 is the undetermined fundamental frequency. Solving (7) obtains
()
Differentiating (8) with respect to t and using (6) and (7), give
()
For the simplification of (9), a third-order nonlinear transformation is considered as
()
where , i = 1,2, 3.
These transformation coefficients Γj,i−j are suitably chosen to eliminate the nonresonance terms [9] in the final expression. So the normal form of (9) is
()
Next, η, require to be expressed in the following polar form , . Then separating the real and imaginary parts of the foregoing equation by considering the stationary condition , we have
()
Hence, (12) produces the amplitude and the undetermined fundamental frequency
()

3. Criterion for the Period-Doubling Bifurcation

Substituting (13) into (7), we obtain the expression of periodic solution in the trigonometric form so that the solution changes into the Cartesian form with the transformation x0 = v − μu, y0 = u. Consider
()
Note that the limit cycle cannot show period-doubling as long as it lies in the center manifold because the latter is two-dimensional and trajectories cannot self-intersect. So it marks z0 on the limit cycle for the expression obtained from (2). To investigate the stability, we append disturbance to z in (1), that is,
()
and linearize the variation z1
()
The general solution of (16) is
()
where . By considering the Floquet theory, the transition from stable to unstable occurs in the condition of z1(T) = z1(0), where T is the period of the limit cycle oscillation. That produces the critical value of period-doubling bifurcation through M(μc) = 0, and the result is
()

In order to illustrate the accuracy of the result, the critical values obtained from different methods are presented in Table 1.

Table 1. Critical value for the first period-doubling bifurcation.
Method Numerical simulation This paper Reference [4] Reference [6]
μc 0.439 0.443 0.45 0.446
Finally, we investigate the stability to find the critical values of the second period doubling bifurcation. That is, from a bifurcation point, the asymmetric 2T-orbit born at the first period-doubling bifurcation point becomes nonstable in a flip bifurcation, where a 4T-orbit emerges. Here, we do not want to give too many details about the second period-doubling bifurcation because the computational process is very similar to the first period doubling bifurcation. We mainly follow the stability analyses of Rand [4] and Belhaq et al. [6]. The main difference exists in finding the solution of the 3D system, where we use the undetermined fundamental frequency method. It produces a better approximation of the asymptotical solution. First of all, we give the general solution in a complex form as follows:
()
Then, we may find the normal form of the reduced system. As for the secular terms, they can be regarded as the near resonance according to [9]. We use a near identity transformation from ξ1 to η1,
()
to find the normal form of the system which also includes the subharmonic components in its expression. That can be written in different order: first order η1, second order , , and third order: , , , , . With these secular terms we find the averaged equation of the system and then amplitude and frequency. Finally, we investigate the stability to find the critical values of the second period-doubling bifurcation. The critical values are presented in Table 2. It exhibits a better approximation than the high order analysis given by Belhaq et al. [6].
Table 2. Critical value for the second period-doubling bifurcation.
Method Numerical simulation This paper Reference [6]
μc 0.476 0.481 0.486

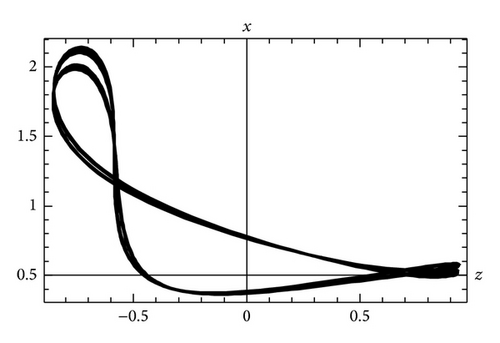
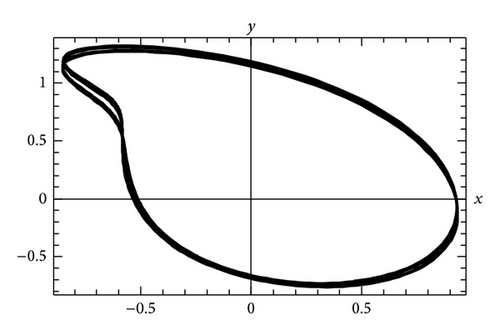
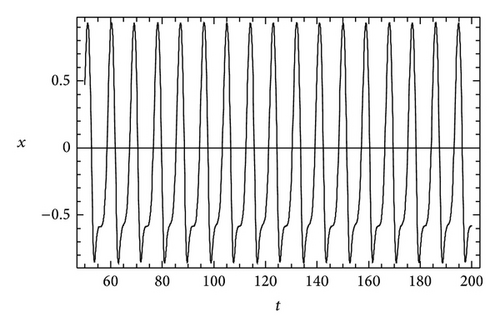
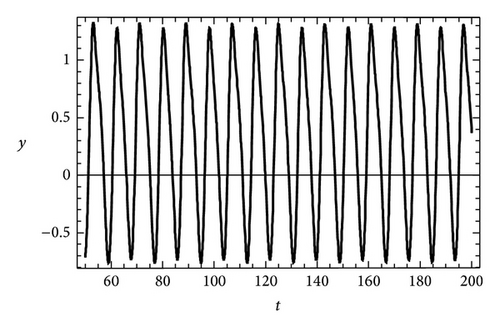
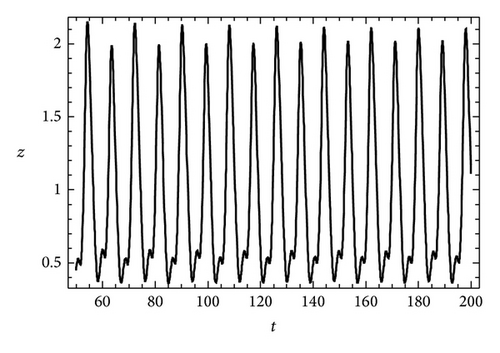
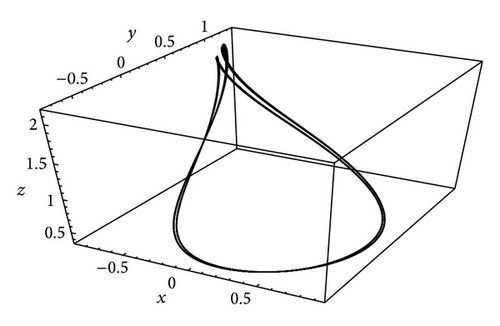
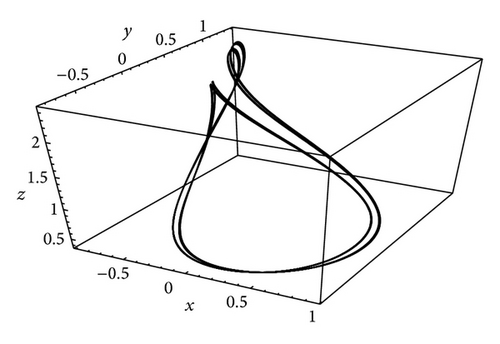
In Figure 1, the projections on (z, x), (x, y), and (y, z) plane are plotted at the value of μc = 0.439. Meanwhile the time series of trajectories x(t), y(t), and z(t) appear in Figure 2. A 3D phase portrait refers to the first and second period-doubling bifurcations that are portrayed at the values μc equal to 0.439 and 0.476 in Figure 3, respectively. Finally we programme the whole computation process in terms of the computer algebra Mathematica to accelerate the analysis more efficiently.

Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
Projections on (z, x), (x, y), and (y, z) plane of the first period-doubling bifurcation.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
Projections on (z, x), (x, y), and (y, z) plane of the first period-doubling bifurcation.
Details are in the caption following the image
Figure 1 (c)
Open in figure viewerPowerPoint
Projections on (z, x), (x, y), and (y, z) plane of the first period-doubling bifurcation.
Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Time series of the first period-doubling trajectories x(t), y(t), and z(t).
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Time series of the first period-doubling trajectories x(t), y(t), and z(t).
Details are in the caption following the image
Figure 2 (c)
Open in figure viewerPowerPoint
Time series of the first period-doubling trajectories x(t), y(t), and z(t).
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
3D phase portrait refers to the first and second period-doubling bifurcation.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
3D phase portrait refers to the first and second period-doubling bifurcation.

4. Conclusion

The strategy of predicting the period-doubling bifurcation of the 3D system is presented by using the undetermined fundamental frequency method. It applies the undetermined fundamental frequency to obtain the stable response of the flows on the center manifold and then forms the criterion of period-doubling prediction by considering the stability of the limit cycle. In contrast to the result of numerical simulation, it reveals a good prediction as shown in Tables 1 and 2, compared with the analytical results of the first and second period-doubling bifurcations given by Rand and Belhaq. The whole process is constituted in terms of the computer algebra Mathematica. It enables people to research the flip bifurcation of the 3D system more accurately and efficiently.

The strategy presented in this work is sufficiently general, so it would be possible to apply the present method to consider other high-dimensional and more complicated systems, which will be the topics for further research.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant no. 11272229) and Science Foundation of Tianjin Education Committee (Grant no. 20120902).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.