This paper proposes a chaos-based secure direct-sequence/spread-spectrum (DS/SS) communication system which is based on a novel combination of the conventional DS/SS and chaos techniques. In the proposed system, bit duration is varied according to a chaotic behavior but is always equal to a multiple of the fixed chip duration in the communication process. Data bits with variable duration are spectrum-spread by multiplying directly with a pseudonoise (PN) sequence and then modulated onto a sinusoidal carrier by means of binary phase-shift keying (BPSK). To recover exactly the data bits, the receiver needs an identical regeneration of not only the PN sequence but also the chaotic behavior, and hence data security is improved significantly. Structure and operation of the proposed system are analyzed in detail. Theoretical evaluation of bit-error rate (BER) performance in presence of additive white Gaussian noise (AWGN) is provided. Parameter choice for different cases of simulation is also considered. Simulation and theoretical results are shown to verify the reliability and feasibility of the proposed system. Security of the proposed system is also discussed.

1. Introduction

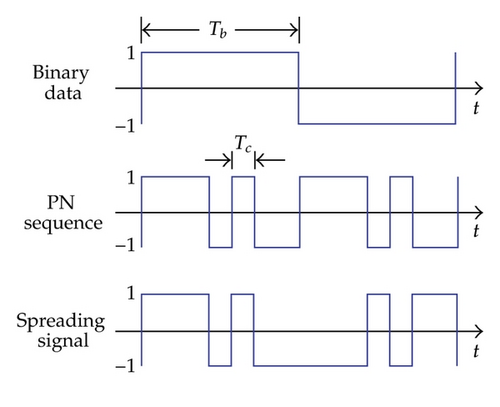
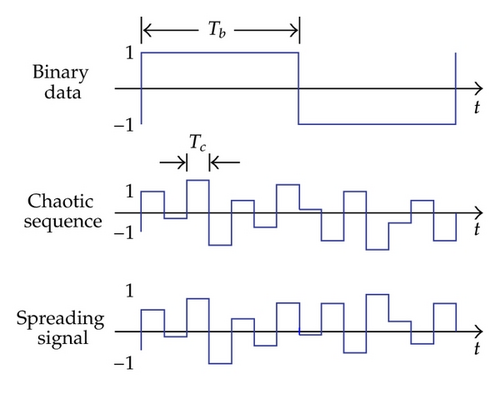
Studying the possibilities of using chaotic behavior [1, 2] to improve features of communication systems has received significant attention in the last several years [3–5]. Many chaos-based communication systems were proposed [6, 7] and most of them exploited chaotic behavior to convey information. Communication systems based on combination of direct-sequence/spread-spectrum (DS/SS) and chaos techniques were presented in [8–10]. It is well known that DS/SS is considered as a main technique of spread-spectrum digital communications [11, 12]. The main difference between the conventional and chaos-based DS/SS systems is the use of spreading sequence. Instead of using the pseudonoise (PN) sequence [13, 14] as in the conventional system, the spread- and despread-spectrum processes in the chaos-based system are carried out by multiplying directly the binary data with a chaotic sequence generated by a chaotic map [1, 2, 15, 16]. Time domain signals shown in Figures 1(a) and 1(b) illustrate the difference in the conventional and chaos-based DS/SS systems, where T_b and T_c are fixed bit and chip durations, respectively.

Details are in the caption following the image — **Figure 1 (a) The conventional DS/SS system [11]**
Open in figure viewer PowerPoint

Time domain signals of the spread-spectrum process in the conventional and proposed DS/SS systems.

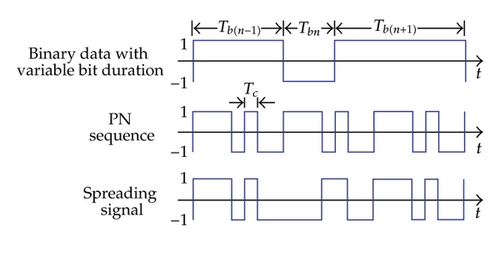
In this paper, we propose a chaos-based secure DS/SS communication system which is the combination of the DS/SS and chaos techniques. Bit duration is varied according to the behavior of chaotic map but always equal to a multiple of the fixed chip duration. Variation in bit duration makes the difference between our proposed system and the conventional ones. The data bits with variable duration are spread in the frequency domain by multiplying directly with the PN sequence and then modulated onto a sinusoidal carrier by means of the binary phase-shift keying (BPSK) [17, 18]. The spread-spectrum process of our proposed chaos-based DS/SS system is illustrated by time domain signals as in Figure 1(c), where T_bn is the variable duration of the nth bit. Since the proposed system operates based on the DS/SS using PN sequence, it inherits all advantages such as interference rejection, antijamming, fading reduction, multiaccess potential, and low probability of interception from the conventional DS/SS system [11, 12]. In addition, data security is improved significantly since the despread-spectrum and data recovery process needs an identical regeneration of both the PN sequence and chaotic behavior.

In the remainder of the paper, the structure and operation of the proposed communication system is presented in Section 2. Theoretical evaluation of BER performance in presence of additive white Gaussian noise (AWGN) is provided in Section 3. Section 4 presents analysis of parameters choice for the system, based on that specific parameters for different cases of simulation system are chosen with proper values. Simulation results are then shown to verify the theoretical ones. Discussions on security features are presented in Section 5. Finally, the conclusion with some final remarks is given in Section 6.

2. Structure and Operation of Chaos-Based Secure DS/SS Communication System

In this section, we present a detailed analysis of the structure and operation of the chaos-based DS/SS communication system proposed. Basically, the proposed system is built around a variable-position pulse and PN sequence (VPP-PNS) generator. Block diagrams of the proposed system and that of the VPP-PNS generator are illustrated in Figures 2(a) and 2(b), respectively.

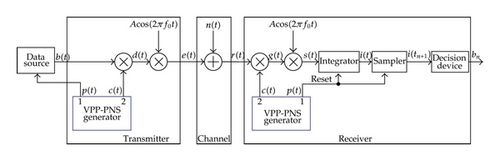
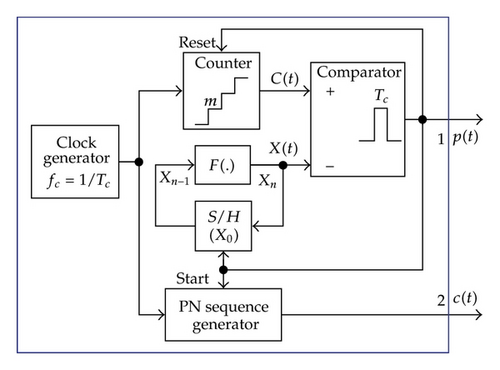
2.1. VPP-PNS Generator

In the VPP-PNS generator, clock pulses with a fixed frequency, f_c = 1/T_c, at the output of the clock generator are fed to the counter and the PN generator. At the initial instance t₀, the clock generator starts working and the sample-and-hold block (S/H as in Figure 2) is loaded initial value X₀. The counter operates in free running mode to produce a discretely increasing signal, C(t) = m · (t − t₀) = mNT_c, at its output, where m is count-step (i.e., the increasing value in a clock cycle T_c) and N is the count-number (i.e., the number of input clock pulses from the initial instance). When the signal C(t) reaches the value, X₁ = F(X₀), at the output of the nonlinear converter (i.e., the block F(·) using the one-dimension chaotic map, X_n = F(X_n−1)), the comparator generates a pulse with a fixed width T_c at the instance, t₁ = t₀ + N₀ T_c. The position of pulse at the output 2 is determined by the interval, t₁ − t₀ = ⌊X₁/m⌋, with ⌊·⌋ being the floor function. This pulse simultaneously triggers the PN sequence generator to start working and to allow S/H storing the value X₁. After that it triggers the counter to reset the count-number to zero. New iteration starts and pulses will be generated as in the above description. In general, the pulse train at the output 1 is expressed as follows:

()

where the nth pulse is generated at the instance

()

and its position is determined by the interval

()

is the rectangular pulse shaping function given by

()

It can be seen that the position of output pulses p(t) varies according to the chaotic signal X(t). With a specific initial instance t₀, (3) points out that variation of position depends on the chaotic map F(·), initial value X₀, and count-step m.

The PN sequence generated at the output 2 with the fixed chip duration of T_c is expressed by a nonreturn-zero (NRZ) pulse train as follows:

()

where

and N_n are the binary values (i.e., {±1}) of the kth chip and the number of chips in the duration of [t_n, t_n+1], respectively; the function

is as in (4).

2.2. Transmitter

In the transmitter, each pulse of the train p(t) triggers the data source to shift the data bit to the output. It means that the nth bit is shifted at the instance t_n and its duration is equal to the interval of [t_n, t_n+1]. Based on (2), the duration of the nth bit is determined by

()

Equation (6) shows that the bit duration varies according to the chaotic signal X(t) and depends on F(·), X₀, and m. With a certain chaotic map F(·), in the iteration process, its output values vary chaotically in the dimensionless range of [X_min, X_max]. This leads to the variation in the bit duration within the time range of [T_bmin, T_bmax] in the communication process. Since the chip duration T_c is fixed, the number of chips per bit, N_n = T_bn/T_c, called the spreading factor, also varies in the range of [N_min, N_max] what is determined in (6) as

()

In the design process, the values of the parameters T_c, N_min, and N_max are predetermined to guarantee desired specifications of the system such as the bandwidth, average bit rate, and BER. The chaotic map F(·), the range of [X_min, X_max], and the count-step m are then chosen so as to satisfy (7). The analysis of this choice will be presented in Section 4.1.

The binary data with variable bit duration at the output of the data source is formatted in NRZ pulses and expressed by

()

where b_n is the binary value (i.e., {±1}) of the nth bit, and

is the rectangular pulse shaping function defined by

()

The spectrum spreading process is carried out by multiplying the data b(t) with the PN sequence c(t). The spreading signal d(t) is then modulated onto a sinusoidal carrier by means of BPSK, producing the DS/SS-BPSK signal given by

()

with A and f₀ being the amplitude and frequency of the carrier, respectively. The resulting signal e(t) is transmitted at the output of the transmitter.

2.3. Receiver

The VPP-PNS generators in the transmitter and receiver are designed to work as digital modules which can be implemented on the programmable devices such as the field programmable gate array (FPGA), digital signal processing (DSP), and microprocessor (MP). In practice, this design can be guaranteed such that there is nearly no parameters mismatch between the VPP-PNS generators. It means that the variable-position pulse train and PN sequence regenerated in the receiver are identical to those in the transmitter. Therefore, we can apply the available synchronization methods of the conventional DS/SS system [11, 12, 18] for the proposed system. Here, for simplicity, the operation of the receiver assumes that the synchronization in the sinusoidal carrier, variable-position pulse train, and PN sequence is established and maintained.

The received signal r(t) at the input is the sum of the transmitted signal e(t) and channel noise n(t). Firstly, the received signal is multiplied with the PN sequence as follows:

()

and then the resulting signal g(t) is mixed with the sinusoidal carrier by

()

The signal s(t) is fed to the integrator whose output is reset to zero by the trigger of each pulse of the train p(t). It means that the integration period of each bit is equal to the corresponding interpulse interval which is also the corresponding bit duration. Before each reset instance, the output signal of the integrator, i(t), is sampled. The output value of the sampler at the instance t_n+1 is determined by

()

where (A²/2b_n)T_bn is the energy of the desired signal;

equal to zero because the period T_bn is a multiple of the carrier cycle (i.e., T₀ = 1/f₀);

is the energy produced by the channel noise. It is noted that the correlation between c(t) and An(t)cos(2πf₀t) is very low and hence the noise energy is much less than the signal energy. Finally, the resulting sample is fed to the decision device to recover the binary value of the nth bit as follows:

()

3. Theoretical Evaluation of BER Performance

In this section, BER performance of the proposed communication system with the channel noise being AWGN is evaluated theoretically. In the receiver, at each sampling instance, an error decision leading to an error bit occurs when the noise energy exceeds the signal energy in the opposite direction. Therefore, signal-to-noise ratio (SNR) of each output sample is a key parameter for estimating the BER of the system. Let us consider the value of the (n + 1)th sample with two energy component as given in (13). The first component is the signal energy whose absolute magnitude is determined by

()

The second one is the noise energy which is a random variable depending on the zero-mean Gaussian noise n(t) and thus its mean is also zero, while its variance can be calculated as follows:

()

where E[·] is the statistical expectation and N₀ is the noise power spectral density. The SNR of the (n + 1)th sample, SNR_n, is determined as the absolute magnitude of the signal energy, S_n, divided by the root-mean-square noise

[19], so we have

()

where E_c = A²T_c/2 is fixed, and called the energy per chip; the ratio E_c/N₀ is known as the SNR per chip. It can be seen from (17) that the SNR of each output sample depends on the ratio E_c/N₀ and the corresponding spreading factor N_n. Therefore, the SNR for general case of the spreading factor being equal to N is given by

()

In our proposed system, since the spreading factor varies from N_min to N_max in the communication process, the BER is estimated approximately by

()

where p_N is the probability to the spreading factor being equal to N, and

is the BER of the system for case of the spreading factor being equal to N. Assume that the chaotic values distribute uniformly in [X_min, X_max]. It means that the probability p_N is the same for all values of N ∈ [X_min, X_max], so we have

()

Based on the evaluation result of the error probability for the conventional DS/SS-BPSK system as mentioned in [20, 21], the

is determined according to the

()

From the obtained results in (18), (19), (20), and (21), the theoretical evaluation of the BER performance for the proposed communication system is given by the following:

()

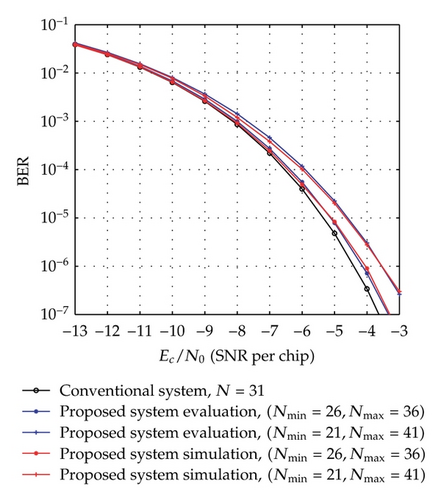
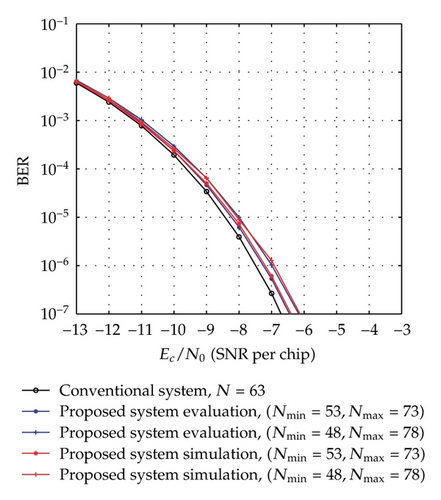
The evaluation BER performances according to (22) for different cases of [N_min, N_max] with the same average spreading factor as well as their comparison with the performance of the equivalent conventional system are shown in Figure 3. With the above assumption of the uniformly distributed chaotic values, the average spreading factor and average bit rate are determined by N_av = (N_min + N_max)/2 and BR_av = 2/((N_min + N_max)T_c), respectively. In Figure 3(a), the performances of the proposed system for the cases of [N_min = 26, N_max = 36] and [N_min = 21, N_max = 41], are compared to each other and to that of the conventional system [21] which has a fixed spreading factor, N = N_av = 31. It can be seen that the proposed system with the case of [N_min = 26, N_max = 36] performs slightly worse than the conventional system with N = 31 and better than the [N_min = 21, N_max = 41] case. Similarly, we can observe from Figure 3(b) that the performance of [N_min = 53, N_max = 73] case is between those of the conventional system with N = 63 and the case of [N_min = 48, N_max = 78]. It is clear that the performance of the proposed system with [N_min, N_max] is poorer than that of conventional system with N = N_av. In addition, the difference between the performance of the proposed system and that of conventional one tends to diminish as the average value (N_min + N_max)/2 gets closer to N = N_av.

4. Parameter Choice and Simulation Results

This section presents the analysis of parameter choice for the proposed system. Based on the analysis, the specific parameters for different cases of the simulation system are chosen with proper values. The simulation results are then shown in order to verify all the theoretical analyses and results obtained.

4.1. Parameter Choice

In order to guarantee the desired specifications of the system such as the bandwidth (i.e., BW = 1/T_c), average bit rate (i.e., BR_av = 2/((N_min + N_max)T_c)), and BER (i.e.,

according to (22)), the values of parameters T_c, N_min, and N_max are predetermined. The chaotic behavior of the chaotic map F(·) is based on that of a conventional chaotic map, x_n = f(x_n−1), denoted by f(·), whose output values vary in a known range of [x_min, x_max]. The parameters T_c, N_min, and N_max and the map f(·) are considered as the predetermined parameters of the system. Using these predetermined parameters, the count-step m and the chaotic map F(·) are chosen as follows:

()

It is easy to find that the output value of the chaotic map F(·) varies chaotically in the range of [X_min = x_min + d, X_max = x_max + d] and thus the initial value X₀ will be chosen in this range. Here, d is a shift value chosen to satisfy (7) as follows:

()

The count-step m and the parameters d, X₀ of the map F(·) are called the chosen parameters of the system.

4.2. Simulation Results

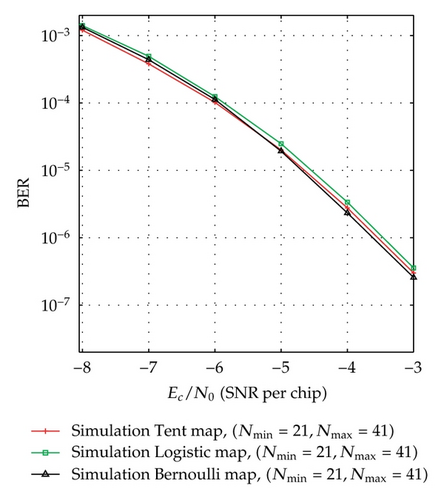
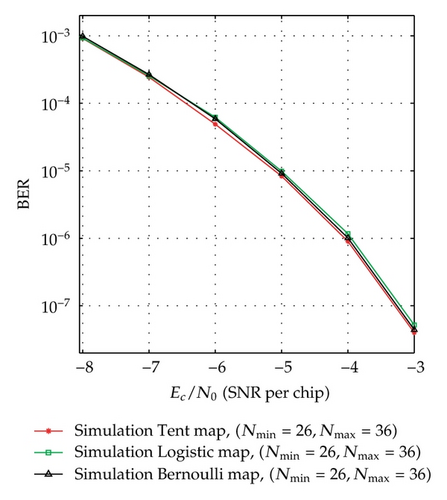
Numerical simulations for different cases of the proposed system with the specific parameters are carried out in Simulink. The values of the predetermined parameters of the simulation system are given as follows: T_c = 1 μs; four cases of [N_min, N_max] = [26, 36], [21, 41], [53, 73], and [48,78]; three conventional chaotic maps simulated in turn are Tent map, Logistic map, and Bernoulli map [1, 2, 15, 16], whose output values vary chaotically in [x_min = 0, x_max = 1]. Based on the choice analysis above, the values of the specifications and chosen parameters of the simulation system corresponding to the different cases of [N_min, N_max] are determined and shown as in Table 1.

Table 1. Specific parameters of the simulation system for cases of [N_min, N_max] = [26, 36], [21, 41], [53, 73], [48, 78].

Predetermined parameters			Specifications of system			Chosen parameters
							Chaotic map
T_c	[N_min, N_max]	f(·) : x_n = f(x_n − 1) [x_min = 0, x_max = 1]	BW	BR_av	BER	m	F(·) : X_n = F(X_n−1) [X_min = d, X_max = d + 1]	d	X₀
	[26, 36]	Tent map: x_n = 2\|0.5 − \|0.5 − x_n−1\|\|		32.25 Kbps	Blue lines in Figure 2(a)	0.1/μs	X_n = 2\|0.5−\|0.5 − (X_n−1 − d)\|+d\|	2.65	2.7
1 μs	[21, 41]	Logistic map: x_n = 4x_n−1(1 − x_n−1)	1 MHz	32.25 Kbps	Blue lines in Figure 2(a)	0.05/μs	X_n = 4(X_n−1 − d)(1 − (X_n−1 − d)) + d	1.075	1.1
	[53, 73] [48, 78]	Bernoulli map: x_n = (2x_n−1) mod 1		15.87 Kbps	Blue lines in Figure 2(b)	0.05/μs 0.033/μs	X_n = ((2(X_n−1 − d)) mod 1) + d	2.675 1.616	2.7 1.7

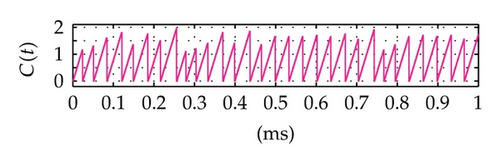
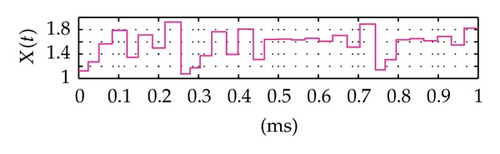
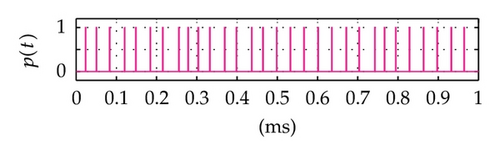
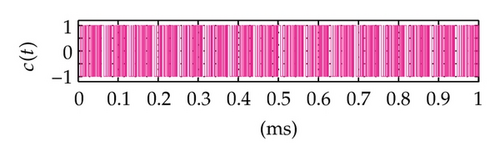
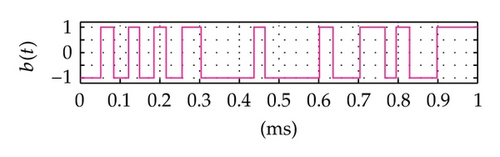
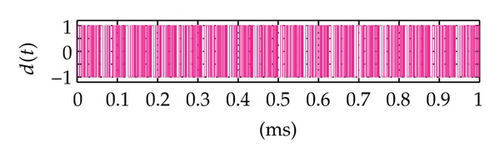
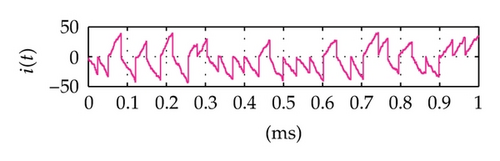
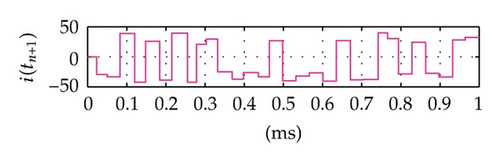
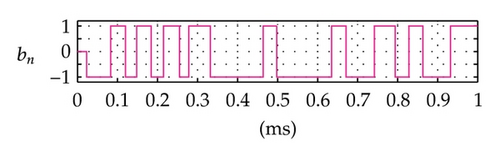
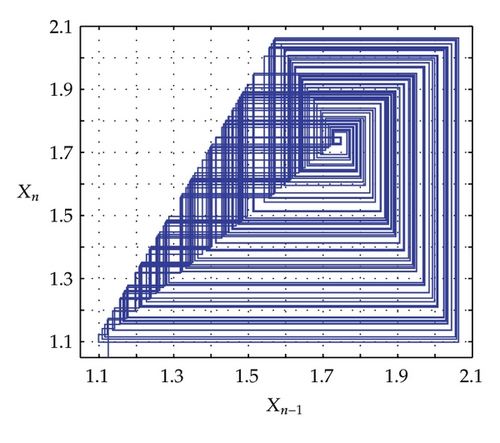
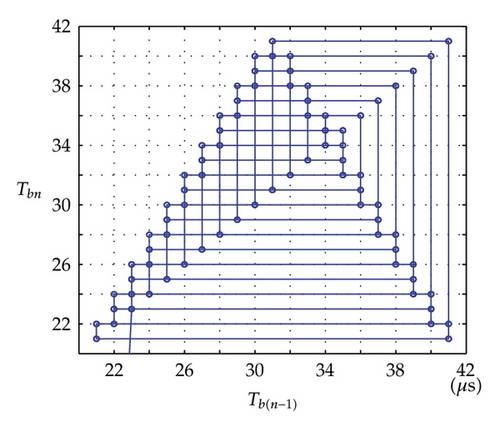
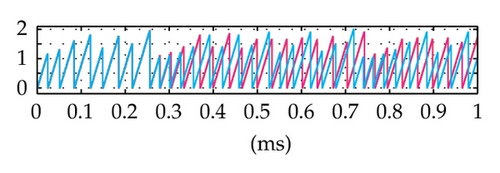
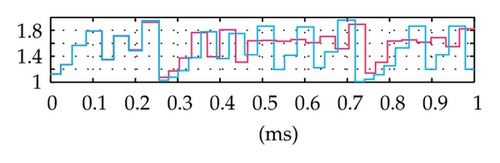
Time domain signals obtained from the simulation system using Tent map for the case of [N_min = 21, N_max = 41] within duration from the starting time 0 to 1000 μs are presented in Figure 4. When the synchronization state of system is established and maintained, the signals of the VPP-PNS generators in the transmitter and receiver are identical and shown as in Figures 4(a)–4(d). The baseband signals in the transmitter and receiver are given in Figures 4(e)-4(f) and Figures 4(g)–4(i), respectively. The chaotic behavior the nonlinear converter F(·) is seen by the attractor diagram in Figure 5(a). It is clear that this is the attractor of Tent map after being shifted with a positive value, d = 1.075. The variation in bit duration according to the chaotic behavior is given in the diagram as in Figure 5(b), where each point expresses the relation between the duration of previous bit and that of the present one. It can be seen that the bit duration varies in the range of [T_bmin = 21 μs, T_bmax = 41 μs].

BER performance of the simulation system using Tent map for the cases of [N_min = 26, N_max = 36], [N_min = 21, N_max = 41], [N_min = 53, N_max = 73], [N_min = 48, N_max = 78] is presented in Figure 3 to compare with the corresponding theoretical performance. In order to investigate the performance of the proposed system with different chaotic maps, the simulation systems using Tent, Logistic, and Bernoulli maps for the cases of [N_min = 21, N_max = 41] and [N_min = 26, N_max = 36] are carried out and the result is as shown in Figure 6. Here, the simulation BERs are calculated as the number of error bits divided by the total number of 10⁸ bits transmitted and the channel noise is AWGN. It can be seen from Figure 3, for each case, that the simulation and corresponding evaluation curves are nearly the same. Also, Figure 6 shows that there is a slight difference in the simulation curves of the different chaotic maps. These prove that the theoretical analysis and the result are reasonable and the proposed communication system is totally feasible.

5. Discussion on Security

It is clear that the conventional DS/SS-BPSK system, an intruder can break the security and recover successfully the original data if he detects correctly the PN sequence and the integration period which is equal to bit rate. Since the bit duration is the same and fixed in the observation process, it is not difficult for the intruder to detect exactly bit rate. Several detection methods of bit rate have been presented in [22, 23]. It means that the security of the conventional system mainly depends on the complication of PN sequence.

Since our proposed system is combined by the DS/SS technique using PN sequence and chaotic modulation, the data transmitted by using the proposed system must be more secure from eavesdroppers than that in case of using individual methods. In other words, the security has been compromised by burying chaotic modulation in the conventional DS/SS technique. With the presence of the conventional DS/SS technique in the proposed system, the transmitted signal has properties like random noise and occupies a wide bandwidth with a very low power spectral density on the transmission channel. It means that the proposed system inherits the security advantages from the conventional method such as the anti jamming capability and low probability of detection and interception [24, 25]. In addition, with the variation of bit duration according to the chaotic behavior, the capability to protect data against unauthorized accesses is improved significantly.

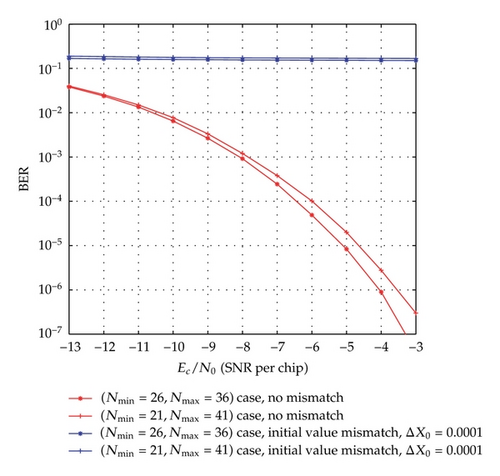
More specifically, the data security of the proposed system is dependent on not only on the complication of PN sequence but also on the variation of the integration period (i.e., the bit duration) according to the chaotic behavior. It is seen that the generation of the chaotic behavior is quite simple for the transmitter and the authorized receiver which has full information on the structure, the value of parameters and functions. In fact, the exact regeneration of chaotic behavior in the proposed system is very difficult for intruders trying to detect them in the context that the chaotic system is covered by the PN sequence generator. Due to the sensitive dependence of the chaotic behavior on the initial value, a very slight error in its detection leads to exponentially increasing errors in the regeneration. In such case, the detection of the variation of bit duration is completely incorrect and the receiver operates in the desynchronization state. As a result, BER will be very high and thus the unauthorized access is failed. These are proved by simulation results in Figures 7 and 8, where the time domain signals and BER performances of the receiver in the case of initial value mismatch (with a very small difference, ΔX₀ = 0.0001) are shown and compared with those in the case of no mismatch. We can observe that after about 0.2 ms from the starting time, the mismatch signals become totally different from the corresponding no-mismatch signals. The BER performance with the mismatch is much worse than that of the cases with no-mismatch. Particularly, although the ratio E_c/N₀ increases gradually, the mismatches in BER are nearly unvaried and approximately equal to 1.6 10⁻¹. It is noticed that the set of values of m, X₀, and F(·) is considered as a secret key. It is hard for the intruder to recover correctly the data without having full information on the structure of the system, the PN sequence, and this secret key. Furthermore, the generation of the chaotic values can easily be made as complicated as is desired. For example, instead of the one-dimension maps, we can use multidimension chaotic ones. Also, several chaotic maps may be combined to increase the number of parameters involved. The initial value can be changed for different communication sessions. All these will improve significantly the security of the proposed method.

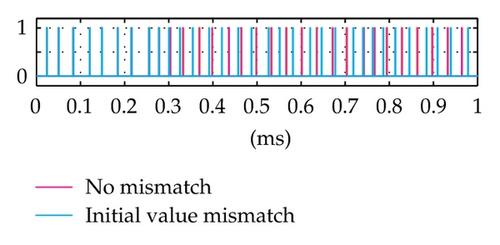
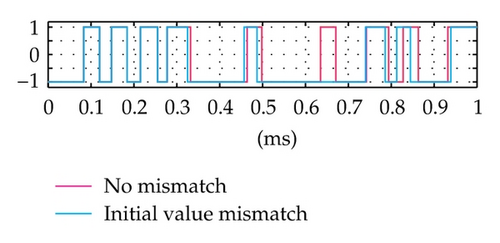
Most of the attack methods are proposed in order to break the chaotic communication systems [26–29] operated based on exploiting properties such as waveform, spectrum, and attractor of the chaotic signal which masks the information and is transmitted directly on the channel. In the proposed system, the signal transmitted on the channel is totally the same as that of the conventional system and without any trace of the chaotic behavior; thus, the existing attack methods are inapplicable to the proposed system. It means that no chance for the intruder to be able to detect the variation of bit duration from the physical signal on the channel. It is also clear that the conventional detection methods of bit rate mentioned above cannot detect in detail this variation. They may detect the variation range and average value of bit duration, but this is not sufficient for a successful access.

6. Conclusion

This study has presented a chaos-based secure DS/SS communication system which is based on a novel combination of the conventional DS/SS and chaos techniques. The structure, operation, and BER performance of the proposed system are described and investigated by means of the theoretical analysis and numerical simulation. The simulation result agrees with the theoretical analysis. The discussion shows the potential of security improvement. It can be seen from the obtained results, that is, (1) the proposed system inherits all the advantages from the conventional system such as the interference rejection, antijamming, fading reduction, multiaccess capability, and low probability of interception due to its operation also based on the DS/SS using PN sequence and BPSK technique; (2) with the variation of bit duration according to the chaotic behavior in the communication process, the proposed system not only still maintains an approximately good performance but also achieves significant improvement on the data security in comparison with the equivalent conventional system. All these features make the proposed system feasible and robust for the security required and DS/SS-based digital communication system.

Acknowledgment

This work is supported by the Vietnam’s National Foundation for Science and Technology Development (NAFOSTED) under Grant no. 102.02-2012.34.

References

1 Strogatz S. H., Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, 2001, Westview Press.
Google Scholar
2 Hilborn R. C., Chaos and Nonlinear Dynamics: An introduction for Scientists and Engineer, 2001, The Clarendon Press Oxford University Press, 1263025.
Google Scholar
3 Kennedy M. P., Rovatti R., and Setti G., Chaotic Electronics in Telecommunications, 2000, CRC Press.
Google Scholar
4 Kennedy M. P. and Kolumbán G., Special issue on noncoherent chaotic communications, IEEE Transactions on Circuits and Systems I. (2000) 47, no. 12, 1661–1662.
10.1109/TCSI.2000.899917
Google Scholar
5 Abel A. and Schwarz W., Chaos communications—Principles, schemes, and system analysis, Proceedings of the IEEE. (2002) 90, no. 5, 691–710, 2-s2.0-1442273672, https://doi.org/10.1109/JPROC.2002.1015002.
10.1109/JPROC.2002.1015002
Web of Science® Google Scholar
6 Lau F. C. M. and Tse C. K., Chaos-Based Digital Communication Systems: Operating Principles, Analysis Methods, and Performance Evaluation, 2003, Springer.
10.1007/978-3-662-05183-2
Google Scholar
7 Stavroulakis P., Chaos Applications in Telecommunications, 2005, CRC Press.
Google Scholar
8 Heidari-bateni G. and McGillem C. D., Chaotic direct-sequence spread-spectrum communication system, IEEE Transactions on Communications. (1994) 42, no. 2, 1524–1527, 2-s2.0-0028369325.
10.1109/TCOMM.1994.582834
Web of Science® Google Scholar
9 Heidari-Bateni G. and McGillem C. D., Chaotic sequences for spread spectrum: an alternative to PN-sequences, Proceedings of the IEEE International Conference on Selected Topics in Wireless Communications, June 1992, Vancouver, Canada, 437–440.
Google Scholar
10 Kurian A. P., Puthusserypady S., and Htut S. M., Performance enhancement of DS/CDMA system using chaotic complex spreading sequence, IEEE Transactions on Wireless Communications. (2005) 4, no. 3, 984–989, 2-s2.0-18844393435, https://doi.org/10.1109/TWC.2005.847028.
10.1109/TWC.2005.847028
Web of Science® Google Scholar
11 Peterson R. L., Zeimer R. E., and Borth D. E., Introduction to Spread Spectrum Communications, 1995, Prentice Hall, New York, NY, USA.
Google Scholar
12 Simon M. K., Omura J. K., Scholtz R. A., and Levitt B. K., Spread Spectrum Communications, 1985, Computer Science Press.
Google Scholar
13 Dinan E. H. and Jabbari B., Spreading codes for direct sequence CDMA and wideband CDMA cellular networks, IEEE Communications Magazine. (1998) 36, no. 9, 48–54, 2-s2.0-0032165148.
10.1109/35.714616
Web of Science® Google Scholar
14 Sarwate D. V. and Pursley M. B., Crosscorrelation properties of pseudorandom and related sequences, Proceedings of the IEEE. (1980) 68, no. 5, 593–619, 2-s2.0-0019021287.
10.1109/PROC.1980.11697
Web of Science® Google Scholar
15 Devaney R. L., An Introduction to Chaotic Dynamica Systems, 1989, Second edition, Addison-Wesley, Reading, Mass, USA, 1046376.
Google Scholar
16 Schuster H. G., Deterministic Chaos, an Introduction, 1984, Physick, Weinheim, Germany, D-6940.
Google Scholar
17 Frank R. L. and Zadoff S. A., Phase shift pulse codes with good periodic correlation properties, IRE Transactions on Information Theory. (1962) 8, 381–382.
10.1109/TIT.1962.1057786
Web of Science® Google Scholar
18 Proakis J., Digital Communications, 2000, 4th edition, McGraw-Hill, New York, NY, USA.
Google Scholar
19 Pursley M. B., Performance evaluation for phase-coded spread-spectrum multiple-access communication—part I: system Analysis, IEEE Transactions on Communications. (1977) 25, no. 8, 795–799, 2-s2.0-0017523322.
10.1109/TCOM.1977.1093915
Web of Science® Google Scholar
20 Morrow R. K. and Lehnert J. S., Bit-to-bit error dependence in slotted DS/SSMA packet systems with random signature sequences, IEEE Transactions on Communications. (1989) 37, no. 10, 1052–1061, 2-s2.0-0024751335.
10.1109/26.41160
Web of Science® Google Scholar
21 Holtzman J. M., A simple, accurate method to calculate spread-spectrum multiple-access error probabilities, IEEE Transactions on Communications. (1992) 40, no. 3, 461–464, 2-s2.0-0026823866, https://doi.org/10.1109/26.135712.
10.1109/26.135712
Web of Science® Google Scholar
22 Reed D. E., Comparison of symbol-rate detector and radiometer intercept receiver performances in a nonstationary environment, 1, Proceedings of the IEEE Military Communications Conference, October 1989, Boston, Mass, USA, 1951–1955, 2-s2.0-0024936550.
Google Scholar
23 Burel G., Bouder C., and Berder O., Detection of direct sequence spread spectrum transmissions without prior knowledge, Proceedings of the IEEE Global Telecommunicatins Conference, November 2001, 236–239, 2-s2.0-0035685002.
Google Scholar
24 Dillard R. A., Detectability of spread-spectrum signals, IEEE Transactions on Aerospace and Electronic Systems. (1979) 15, no. 4, 526–537, 2-s2.0-0018495691.
10.1109/TAES.1979.308737
Web of Science® Google Scholar
25 Schoolcraft R., Low probability of detection communications–LPD waveform design and detection techniques, 2, Proceedings of the Military Communications Conference, November 1991, McLean, Va, USA, 3531–3539, 2-s2.0-0026380035.
Google Scholar
26 Short K. M., Steps toward unmasking secure communication, International Journal of Bifurcation and Chaos. (1994) 4, no. 4, 959–977.
10.1142/S021812749400068X
Web of Science® Google Scholar
27 Short K. M., Unmasking a modulated chaotic communications scheme, International Journal of Bifurcation and Chaos. (1996) 6, no. 2, 611–615.
10.1142/S0218127496000114
Web of Science® Google Scholar
28 Sobhy M. I. and Shehata A. R., Methods of attacking chaotic encryption and countermeasures, 2, Proceedings of the IEEE Interntional Conference on Acoustics, Speech, and Signal Processing, May 2001, 1001–1004, 2-s2.0-0034856253.
Google Scholar
29 Álvarez G., Montoya F., Romera M., and Pastor G., Breaking parameter modulated chaotic secure communication system, Chaos, Solitons and Fractals. (2004) 21, no. 4, 783–787, 2-s2.0-1542290089, https://doi.org/10.1016/j.chaos.2003.12.041.
10.1016/j.chaos.2003.12.041
Web of Science® Google Scholar

Citing Literature

All articles

A Chaos-Based Secure Direct-Sequence/Spread-Spectrum Communication System

Abstract

1. Introduction