Mathematical models, such as sets of equations, are used in engineering to represent and analyze the behaviour of physical systems. The conventional notations in formulating engineering models do not clearly provide all the details required in order to fully understand the equations, and, thus, artifacts such as ontologies, which are the building blocks of knowledge representation models, are used to fulfil this gap. Since ontologies are the outcome of an intersubjective agreement among a group of individuals about the same fragment of the objective world, their development and use are questions in debate with regard to their competencies and limitations to univocally conceptualize a domain of interest. This is related to the following question: “What is the criterion for delimiting the specification of the main identifiable entities in order to consistently build the conceptual framework of the domain in question?” This query motivates us to view the Yoneda philosophy as a fundamental concern of understanding the conceptualization phase of each ontology engineering methodology. In this way, we exploit the link between the notion of formal concepts of formal concept analysis and a concluding remark resulting from the Yoneda embedding lemma of category theory in order to establish a formal process.

1. Introduction

In the computer science context, the terms ontology and concept are defined in many various ways, and sometimes their use is a confused mixture of both terms. On the one hand, an ontology is defined as a common conceptualization of a general idea, or a domain of interest [1, 2], while, on the other hand, a concept is defined as a general idea, which is created by removing the uncommon characteristics from several particular ideas [3]. Thus, it is obvious that ontologies use concepts to convey their semantics and concepts are definitional structures that are explicitly encoded within ontologies.

In practice, an ontology consists of classes that are concepts of a particular domain, relations between classes, a hierarchy of classes, properties of classes that describe their attributes, instances of classes with specific values, and axioms that specify additional constraints over classes. So, the most crucial task of building an ontology is to consistently express its classes, that is, the concepts of a particular domain. An indispensable condition for formally expressing a concept that should carry a meaning, besides its name that does not carry any meaning, is to determine all its stakeholders, that is, other terms interrelated with the concept in question, properties attached to it, and specific values, directly or indirectly, affecting its noema, since, in natural language, a concept can be described by the objects belonging to it or by its determining features [4].

In order to make the ontological status of concepts apparent, independently of the language used to express them and of the techniques used for embedding them within ontologies, we have exploited the link between the notion of formal concepts of formal concept analysis (FCA) and a concluding remark resulting from the Yoneda embedding lemma of category theory. This enables the formalization of concepts by considering their semantics, since the notion of a concept in computer science is very subtle and does not rely on mathematical constructors. This step intends to eliminate any misunderstanding that occurs, due to ontological semantic heterogeneity, arising from synonymy (i.e., ontological concepts for a domain described with different terminologies) and polysemy (i.e., different meanings assigned to the same word in different contexts).

The basics and the role of formal concept analysis in defining ontology concepts are discussed in Sections 2 and 4, respectively, while the basics and a discussion of related work on category theory are presented in Sections 3 and 5, respectively. In Section 6, the main point of this work is illustrated, by means of a simple example. In Section 7, other possible meeting points of FCA and category theory, aiming at direct research into the critical path of formalizing tasks concerning ontology engineering and facilitating progress of the field, are discussed. The conclusion is drawn in the last section.

2. Formal Concept Analysis Background: Formal Context, Formal Concept, and Concept Lattice

This section introduces basic terms of formal concept analysis, among which are the fundamental notions of a formal context, formal concept, and concept lattice, as well as their basic properties.

Formal concept analysis (FCA), introduced by Wille [5], is a method for analyzing data which describe relationships between a set of objects and a set of attributes. From the input data, FCA produces a concept lattice, which is a collection of formal concepts in the data. Formal concepts are clusters of data drawn together by having common attributes [6] representing natural human-like concepts and are hierarchically ordered by a subconcept-superconcept relation. FCA also produces attribute implications which describe particular dependencies valid in the data. It integrates the discovery and reasoning with concepts in data, the discovery and reasoning with dependencies in data and the visualization of data, and concepts and dependencies with folding and unfolding capabilities, which are referred to as the reconstruction of a diagram of concepts and their dependencies, in order to be more simplified, but as informative as the original one. For more details see [7, 8].

In FCA, a cross-table with logical attributes is represented by a triplet 〈X, Y, I〉 (a so-called context), where the elements of the set X are called objects and correspond to the rows of the table, the elements of the set Y are called attributes and correspond to the columns of the table, and I is a binary (incidence) relation between X and Y. 〈x, y〉 ∈ I, or xIy indicates that object x has attribute y or that y holds for x, while 〈x, y〉 ∉ I indicates that object x does not have attribute y. An example of such a table is shown in Table 1.

Table 1. A table defining an incidence relation.

	y₁	y₂	y₃
x₁	×	×	×
x₂	×	×
x₃		×	×

A partially ordered collection of particular clusters of objects and attributes is obtained out of a given context cross-table, and it is called a concept lattice. The clusters of a concept lattice, called formal concepts, are pairs 〈A, B〉, where A⊆X is a set of objects and B⊆Y is a set of attributes, such that A is the set of all objects which have all attributes from B and B is the set of all attributes which are common to all objects from A. For instance, 〈{x₁, x₂}, {y₁, y₂}〉 is an example of a formal concept for the table of Table 1. Under suitable permutations of the rows and the columns of the cross-table, a formal concept 〈A, B〉 is represented by a maximal rectangle full of crosses.

Moreover, formulas describing dependencies which are true in the table are obtained, which are called attribute implications. An attribute implication is an expression A⇒B, with A and B being sets of attributes. A⇒B is true in the context 〈X, Y, I〉 if each object having all attributes from A has all attributes from B as well. For instance, {y₃}⇒{y₂} is true for the context of Table 1, while {y₁, y₂}⇒{y₃} is not, x₂ being a counterexample.

In order to produce the formal concepts of a formal context 〈X, Y, I〉, the so-called concept-forming operators are used, defined between the powersets of X and Y:

()

where A^↑ is just the set of all attributes shared by all objects of A and

()

where B^↓ is just the set of all objects sharing all attributes from B.

A formal concept now in 〈X, Y, I〉 is just a pair 〈A, B〉 of A⊆X and B⊆Y, such that A^↑ = B and B^↓ = A. A is called the extent and B the intent of 〈A, B〉, respectively. The formal concepts are naturally ordered by using a subconcept-superconcept relation, based on inclusion relation on objects and attributes; that is, for formal concepts 〈A₁, B₁〉 and 〈A₂, B₂〉 of the context 〈X, Y, I〉, 〈A₁, B₁〉 ≤ 〈A₂, B₂〉 if and only if A₁⊆A₂ (if and only if B₂⊆B₁).

By using basic mathematical structures behind FCA, it can be proven that the pair 〈↑, ↓〉 of concept-forming operators induced by 〈X, Y, I〉 forms a Galois connection between X and Y, and the formal concepts 〈A, B〉 are just the fixed points of this Galois connection.

More precisely, given a pair of sets X and Y, a pair 〈f, g〉 of operators, f : 2^X → 2^Y and g : 2^X → 2^Y, is a Galois connection if for A, A₁, A₂⊆X, B, B₁, B₂⊆Y it satisfies the following:

()

For a Galois connection 〈f, g〉 between the sets X and Y, the fixpoint set of 〈f, g〉 is defined as the set

()

Also, for a Galois connection 〈f, g〉 between the sets X and Y, we have

()

Now, given a set X, a mapping C : 2^X → 2^X, such that, for each A, A₁, A₂⊆X,

()

is called a closure operator on X and its fixpoint set is given by

()

In addition, for a Galois connection 〈f, g〉 between the sets X and Y, the composition C_X : f ∘ g is the closure operator on X and C_Y : g∘f is the closure operator on Y.

Finally, since the pair 〈↑, ↓〉 of concept-forming operators induced by 〈X, Y, I〉 forms a Galois connection between X and Y, the compositions ↑↓ and ↓↑ of the concept-forming operators are closure operators on X and Y, respectively.

Another fundamental notion in FCA is that of the set of all formal concepts of 〈X, Y, I〉, denoted by ℬ (X, Y, I) the so-called concept lattice, where

()

Then, the fixpoints of the composition operator ↑↓ give the set of all extents of the formal concepts of 〈X, Y, I〉 that is,

()

and the fixpoints of the composition operator ↓↑ give the set of all intents of the formal concepts of 〈X, Y, I〉; that is,

()

The extents and intents are just the images under the concept-forming operators:

()

Hence,

()

Now, a partial order ≤ can be defined on ℬ(X, Y, I), since for 〈A₁, B₁〉, 〈A₂, B₂〉 ∈ ℬ(X, Y, I), A₁⊆A₂ if and only if B₂⊆B₁. Thus, one puts 〈A₁, B₁〉 ≤ 〈A₂, B₂〉, meaning that 〈A₁, B₁〉 is more specific than 〈A₂, B₂〉 or, equivalently, that 〈A₂, B₂〉 is more general than 〈A₁, B₁〉. Then 〈ℬ(X, Y, I), ≤〉 is a complete lattice, which means that, for any collection of formal concepts K⊆ℬ(X, Y, I), ℬ(X, Y, I) contains both their direct generalization (the supremum of K, noted as ∨K) and their direct specialization (the infimum of K, noted as ∧K). The main theorem of concept lattices states that the supremum and infimum of a collection of formal concepts 〈A_j, B_j〉, j ∈ J, J = 1, 2, 3, …, are given by

()

3. Category Theory Background: Categories, Functors, Natural Transformations, and Yoneda Embedding Lemma

In this section, we briefly refer to the basic notions of category theory, such as categories, functors, and natural transformations that guide to the comprehension of the Yoneda embedding lemma.

Category theory [9–12], which can, in general, be considered as a mathematical theory of structures and of systems of structures, occupies a central position in contemporary mathematics and theoretical computer science, since (a) it focuses on relationships (categorical morphisms, functors, and natural transformations) and not on entities (categorical objects and categories), (b) it allows the coexistence of heterogeneous entities, since it provides the ability to define several categories, according to the kind of entities to be described, which can be related by the definition of special morphisms (categorical functors), (c) it offers a set of categorical constructors for creating new categories, by using predefined ones, (d) it provides a means for the combination of categorical objects (colimits can be used to compose them and limits to decompose them) and for the combination of categorical functors (natural transformations), and (e) it provides a multilevel study of its categorical notions, by defining three interrelated levels (the level of categories, of functors, and of natural transformations).

A category is a mathematical structure consisting of entities of some kind, together with the relationships between them that express the structure. Formally, a category consists of objects (entities) and morphisms (relationships), together with a law of composition for the morphisms, and a unique identity morphism for each object. More rigorously speaking, a category 𝒞 is anything comprising the following data.

(i)
A class 𝒞₀ of objects is denoted by A, B, C, ….
(ii)
A class 𝒞₁ of morphisms between objects is denoted by f, g, h, …. In order to denote a morphism f from object A to object B, we write f : A → B, where A is the domain of f(dom f = A) and B is the codomain of f(codf = B). In general, there may exist more than one morphism from A to B. The collection of all morphisms from A to B is denoted by Hom_𝒞(A, B) = 𝒞(A, B).
(iii)
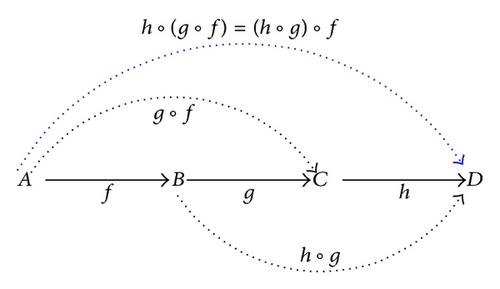
A composition operator is denoted by ∘, assigning to each pair of composable morphisms f : A → B and g : B → C a composite arrow h : A → C, h = g∘f. The composition of morphisms is associative, that is, for any morphisms f : A → B, g : B → C, and h : C → D : h∘(g∘f) = (h∘g)∘f, as depicted in Figure 1.
(iv)
For each object A in 𝒞₀, a unique morphism 1_A : A → A, which acts as the unit of the composition; that is, for any morphism f : A → B, 1_B∘f = f = f∘1_A, as depicted in Figure 2.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The composition operation is associative.

A category 𝒞 is called small when the objects 𝒞₀ and the morphisms 𝒞₁ are sets and not proper classes. A less strict concept is that of a locally small category, when for all objects A and B in 𝒞₀, the collection of morphisms between them, 𝒞(A, B), is a set, called a Hom-set (in this case, we may still have “too many” pairs of objects).

An important category is Set, the category having sets as objects, total functions as morphisms, and identity functions as identity morphisms. The composition of total functions, f : A → B and g : B → C, is the total function h : A → C, mapping a ∈ A to (g∘f)(a) = g(f(a)) ∈ C.

For each category 𝒞, the dual category 𝒞^op is defined as the category having the same objects as those of 𝒞 and as morphisms the opposites of the morphisms in 𝒞; that is, if f : A → B is a morphism in 𝒞₁, then f^op : B → A is a morphism in .

Another essential feature of category theory is that of an isomorphism, which is mainly used in order to compare objects. An isomorphism is a morphism f : A → B that has an inverse, that is, a morphism f⁻¹ : B → A, such that f∘f⁻¹ = 1_B and f⁻¹∘f = 1_A. If f : A → B is an isomorphism, then its inverse f⁻¹ : B → A is unique. By using this definition, two objects A and B are isomorphic (A≅B) if there is a pair of inverse morphisms f : A → B and f⁻¹ : B → A between them. Two isomorphic objects are said to be identical up to an isomorphism if every object satisfying a property p of an object A is isomorphic to A.

There are two special objects that are defined in a category: the initial and the terminal objects. More formally, an object of a category 𝒞 is called an initial object, denoted by 0 in Figure 3, if for every object A in 𝒞, there exists exactly a unique morphism 0 → A.

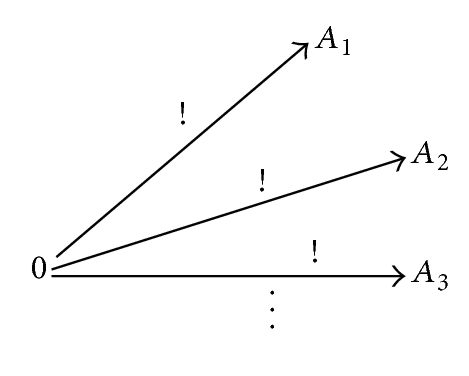
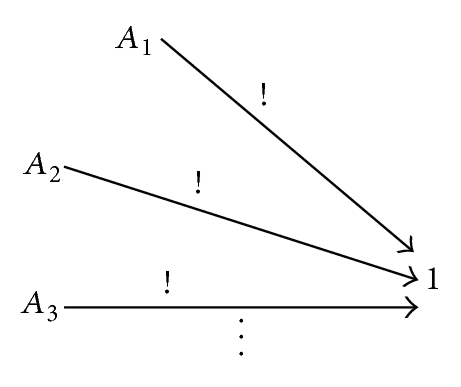
The symbol ! is used to characterize unique morphisms. On the other hand, an object of a category 𝒞 is called a terminal object, denoted by 1 in Figure 4, if for every object A in 𝒞, there exists exactly a unique morphism A → 1.

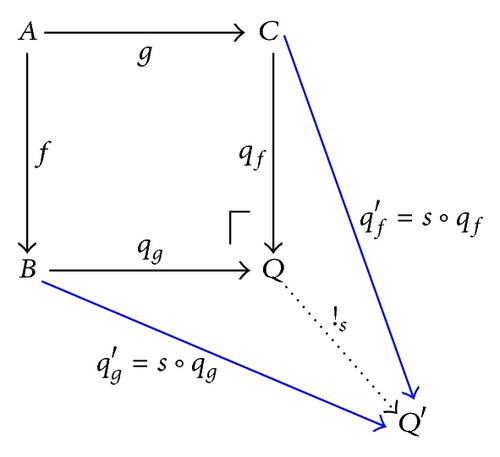
In this mathematical theory, any part of a category can be pictured as a directed diagram, which is a set of objects and morphisms. A significant operation in category theory is the pushout, which is defined over a diagram. A pushout of a pair of morphisms, f : A → B and g : A → C, is an object Q, together with a pair of morphisms q_f : C → Q and q_g : B → Q, such that q_f∘g = q_g∘f, and with the universal property stating that, whenever and are such that , there exists a unique morphism s : Q → Q^′, such that and . In Figure 5, the pushout is indicated by drawing a square corner ⌈ next to it.

The pushout is the categorical dual of pullback, which is depicted in Figure 6, which is obtained by reversing arrows in the graph of pushout.

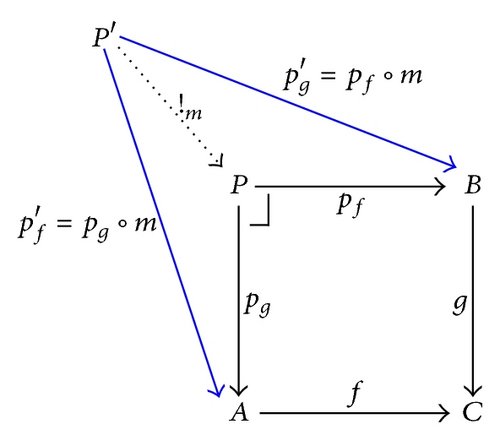
These categorical constructions are characterized as universal constructions, describing a class of objects and the accompanying morphisms that share a common property.

Another important notion of category theory is functors, which are structure-preserving mappings between categories. Given two categories 𝒞 and 𝒟, a functor F : 𝒞 → 𝒟 maps

(i)
each object A ∈ 𝒞 to an object FA ∈ 𝒟,
(ii)
each morphism f : A → B ∈ 𝒞 to a morphism Ff : FA → FB ∈ 𝒟,
(iii)
identity morphisms of 𝒞 to identity morphisms of 𝒟; that is, F(1_A) = 1_FA,
(iv)
the composition of morphisms f and g in 𝒞 to the composition of their mappings in 𝒟; that is, with f and g composable in 𝒞, F(g∘f) = F(g)∘F(f).

For a given category 𝒞, the identity functor 1_𝒞 maps each object and each arrow in 𝒞 to itself. Moreover, functors can be composed. Given two functors F : 𝒞 → 𝒟 and G : 𝒟 → ℰ, their composition G∘F : 𝒞 → ℰ is a functor mapping an object A ∈ 𝒞₀ to the object G(FA) ∈ ℰ₀ and mapping a morphism f ∈ 𝒞₁ to the morphism G(Ff) ∈ ℰ₁.

Let us now consider two locally small categories 𝒞 and 𝒟. For every pair of objects A, B ∈ 𝒞₀, a functor F : 𝒞 → 𝒟 defines a function F_A,B : 𝒞(A, B) → 𝒟(FA, FB) in Set. Then, the functor F : 𝒞 → 𝒟 is

(i)
faithful if the function F_A,B is injective,
(ii)
full if the function F_A,B is surjective,
(iii)
fully faithful if the function F_A,B is bijective.

A functor F : 𝒞 → 𝒟 is an embedding if it is full, faithful, and injective on objects. A functor from 𝒞 to 𝒟 is called a covariant functor, while a functor F : 𝒞^op → 𝒟 is called a contravariant functor from 𝒞 to 𝒟 if it reverses arrow; that is, it is a covariant functor F : 𝒞^op → 𝒟 from the opposite category 𝒞^op to 𝒟.

In order to comprehend the Yoneda embedding, the more elaborate categorical notions of representable functors are needed. The representable functors map a locally small category 𝒞 to the category Set. They refer either to incoming morphisms to a fixed object in 𝒞 (generalized elements) or to outgoing morphisms from a fixed object in 𝒞 (generalized properties).

Given a category 𝒞, the covariant representable functor 𝒞(A, −) : 𝒞 → Set, which is depicted in Figure 7, can be defined, for each fixed object A ∈ 𝒞₀, and it takes each object B ∈ 𝒞₀ to the set 𝒞(A, B) ∈ Set₀ of morphisms from A to B (𝒞(A, B) is an object of Set) and each morphism f : B → C ∈ 𝒞₁ to the function

()

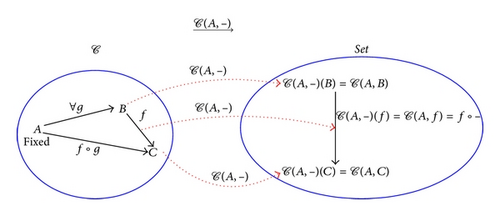
This last function takes a morphism g : A → B ∈ 𝒞₁ (an element of the set 𝒞(A, B) in Set₀) to the morphism 𝒞(A, f)(g) = f∘g ∈ 𝒞₁ (an element of the set 𝒞(A, C) in Set₀). The covariant representable functor refers to the outgoing morphisms from a fixed object A in 𝒞 and to their compositions with other morphisms in 𝒞.

Given a category 𝒞, the contravariant representable functor 𝒞(−, B) : 𝒞^op → Set, which is depicted in Figure 8, is defined, for each fixed object B ∈ 𝒞₀, taking each object A ∈ 𝒞₀ to the set 𝒞(A, B) ∈ Set₀ of morphisms from A to B (𝒞(A, B) is an object of Set) and each morphism f : A → C ∈ 𝒞₁ to the function

()

which takes a morphism g : C → B ∈ 𝒞₁ (an element of the set 𝒞(C, B) in Set₀) to the morphism 𝒞(f, B)(g) = g∘f ∈ 𝒞₁ (an element of the set 𝒞(A, B) in Set₀). The contravariant representable functor refers to the incoming morphisms to a fixed object B in 𝒞 and their compositions with other morphisms in 𝒞.

Moreover, given a category 𝒞, the Hom-set bifunctor 𝒞(−, −) : 𝒞^op × 𝒞 → Set, which is depicted in Figure 9, is defined, for each pair of fixed objects A ∈ 𝒞₀ and B ∈ 𝒞₀, and it takes each such pair of fixed objects A ∈ 𝒞₀ and B ∈ 𝒞₀ to the set 𝒞(A, B) ∈ Set₀ of morphisms from A to B (𝒞(A, B) is an object of Set) and each pair of morphisms f : A^′ → A ∈ 𝒞₁ and g : B^′ → B ∈ 𝒞₁ to the function

()

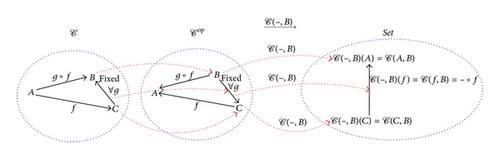
This last function takes a morphism h : A → B ∈ 𝒞₁ (an element of the set 𝒞(A, B) in Set₀) to the morphism 𝒞(f, g)(h) = g∘h∘f ∈ 𝒞₁ (an element of the set 𝒞(A^′, B^′) in Set₀). The contravariant representable functor refers to the incoming morphisms to a fixed object A in 𝒞 and to the outgoing morphisms from a fixed point B in 𝒞.

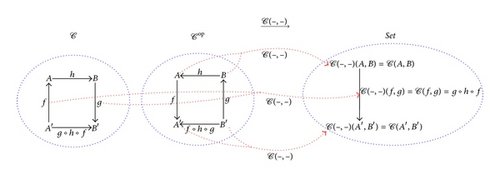
Another important notion of category theory is that of natural transformations, which relate two functors. Given two functors F : 𝒞 → 𝒟 and G : 𝒞 → 𝒟 from 𝒞 to 𝒟, a natural transformation η : F⇒G, which is depicted in Figure 10, is a map h : 𝒞₀ → 𝒟₁, assigning to each object A ∈ 𝒞₀ a morphism η_A : FA → GA ∈ 𝒟₁, called the component of η at A, such that, for every morphism f : A → B ∈ 𝒞₁, it holds that η_B∘Ff = Gf∘η_A. The components η_A are morphisms in 𝒟₁ and can thus be composed.

Given two categories 𝒞 and 𝒟, a functor category denoted by 𝒟^𝒞 is defined, having as objects the functors from 𝒞 to 𝒟 and having as morphisms the natural transformations between them. In this functor category,

is the set of natural transformations from functor F to functor G (F and G are objects of 𝒟^𝒞). The contravariant representable functor for 𝒟^𝒞 is then denoted by Nat(−, G) and sends a functor F ∈ 𝒟^𝒞 to the set Nat(F, G) ∈ Set of natural transformations between F and G and a natural transformation η : F⇒H to the function

()

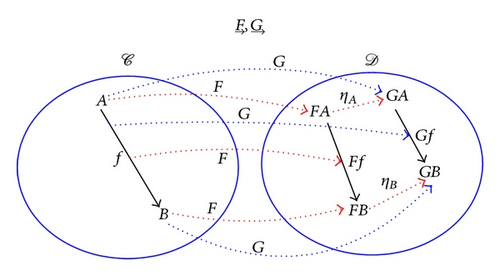
The function Nat(η, G) sends a natural transformation θ : H⇒G to the natural transformation θ ∘ η : F⇒G (which is a morphism in 𝒟^𝒞 and an element of the set Nat(F, G) ∈ Set).

An isomorphism can be defined in a functor category 𝒟^𝒞. Given two functors F, G : 𝒞 → 𝒟 (objects of 𝒟^𝒞), if a natural transformation η : F → G (morphism in 𝒟^𝒞) has an inverse natural transformation η⁻¹ : G → F such that for every object A in C it is and , then η is called a natural isomorphism, and F and G are said to be naturally isomorphic; that is, F≅G.

Given an object A in a category 𝒞, there is a functor from 𝒞 to the category of functors from 𝒞^op to Set (called the category of presheaves) that sends A to the functor . This functor y is the Yoneda embedding. The Yoneda embedding also sends a morphism f : A → B ∈ 𝒞₁ to the natural transformation y_f : 𝒞(−, A) → 𝒞(−, B) between functors 𝒞(−, A) and 𝒞(−, B), having a component at X ∈ C₀, which sends a morphism g : X → A ∈ 𝒞(X, A) to the morphism f∘g : X → B ∈ 𝒞(X, B).

The Yoneda lemma is an abstract result on functors of the type morphisms into a fixed object, which allows the embedding of any category into a category of functors defined on that category. It states that every functor is naturally isomorphic to the functor Nat(y − , F); that is, for every A ∈ 𝒞₀, Nat(yA, F)≅FA and this isomorphism is natural both in A and F. One instance of Yoneda’s lemma is the Yoneda embedding, which informally states that in order to determine an object of a category, it suffices to determine all its generated elements or all its generated properties.

4. The Interplay between FCA and Ontological Concepts

An ontology is the formal expression of relations between relevant notions in order to consistently describe a domain of interest, and in this perspective, it must clearly conceptualize these notions. At the conceptualization level, it is necessary to formally describe the relevant concepts, which are to be included in the ontology.

FCA, on the other hand, is a mathematical theory, which is based on the philosophical statement that a concept is constituted by two parts: its extension consisting of all objects belonging to the concept and its intension comprising all attributes shared by those objects [13]. In FCA, a formal concept is produced from a formal context such as 〈X, Y, I〉 of Section 2 by applying the concept-forming operators to its intension or to its extension; that is, a formal concept is a pair 〈A, B〉, where A⊆X is a set of objects and B⊆Y is a set of attributes, such that A is the set of all objects which have all attributes from B and B is the set of all attributes which are common to all objects from A.

Based on the assumption that an isolated concept has no meaning, since meaning is a product of the relationships among concepts in a specific context, an extension of FCA has been designed, the so-called relational concept analysis (RCA) [14], in order to deal with multirelational data [15]. RCA provides a generalization of FCA in the case of many-valued contexts. A many-valued context is defined as a context (G, M, W, I) consisting of three sets, namely, G, whose elements are called formal objects, M with many-valued attributes, and W, whose elements are values, and a ternary relation I between them, with the conditions (g, m, w) ∈ I and (g, m, v) ∈ I⇒w = v, with (g, m, w) being read as “the attribute m has the value w for the object g.” Thus, relational context schemas are useful for attributes that have not just only one but several values for an object.

Moreover, a triadic approach to FCA has been designed, the so-called triadic concept analysis (TCA) [16], as another FCA extension, which is based on a formalization of the triadic relation connecting objects, attributes, and conditions, where a concept is described by its extension, intention, and modus, respectively [17]. In this framework, instead of the dyadic relation between objects and attributes used in FCA, the triadic approach is based on a triadic relation saying that the object g has the attribute m under the condition b. Similar to the dyadic form of FCA, a triadic concept is produced from a triadic context, which is defined as a quadruple 〈X, Y, Z, I〉, where X, Y, and Z are sets of objects, attributes, and conditions, respectively, and I is a ternary relation between them, by applying derivation operators to its intension, extension, or modus. Thus, triadic concepts can be considered, for example, as those formal concepts that have the same extent but differ according to their intent and modus.

The interplay between FCA and ontologies has been studied to a considerable extent [18]. It turns out that there are basically two ways concerning how FCA and ontological concepts can be combined. The most obvious way is to identify the ontology concepts with the formal concepts of FCA. However, in many applications, the ontology concepts correspond to the FCA attributes [19, 20]. Since the ontological status of concepts has an internal structure, within the framework of FCA, this is sometimes generated by tertiary relations within multivalued contexts [21] or by using distributional formal contexts [22].

The crucial point in specifically describing a concept within an ontology is to find out all the attributes that are shared by this concept. Thus, from an FCA-based point of view, for formally describing a concept, its intentional description is required. In the case where a concept is described by a set of attributes under specific conditions, the notion of triadic contexts is used for its representation [23]. Moreover, each concept within an ontology denotes a specific role emerging from adding specific values to its intentional structure, that is, its attributes. In this perspective, ontology concepts are considered as the relational structures that the RCA process provides [24, 25].

5. The Interplay between Category Theory and Ontological Concepts

Since ontology can be regarded as a categorization of that which exists, issues involving the ontological status of concepts and the notion of a category are important. According to Aristotle, a class or collection of things all of one type, where typicality is determined by a concept, is a category. Later on, a category, as a purely mathematical notion, was defined as having an internal structure given by relationships among members. Thus, the exact match between the terms category and concept has emerged because a concept can be defined as having internal structure, due to their explanatory capabilities [26].

Category theory has been established as an appropriate mathematical basis for the formalization and study of ontologies [27, 28], since it focuses on relationships (categorical morphisms) between entities (categorical objects) in such a way that an entity can be defined according to its interaction with other entities [29]. There have been various category theoretic approaches to ontology engineering, which involves tasks, such as development, mapping, and merging of ontologies. In particular, in the case of ontology mapping and merging, the category Ont of ontologies is defined and the categorical constructions of pullback and pushout are used, respectively [30–32].

Formally speaking, ontology is a theory over logic. But many ontologies are described in different languages, each one with its own logic. Thus, in order to integrate ontologies, many approaches using the theory of institutions [33] have emerged, such as in [34, 35] for mapping between different logics to deal with heterogeneous formalization. Moreover, the constructions of category theory have been combined with information flow theory [36], which describes how information about one thing can convey information about something else, for integrating distributed ontologies [37, 38]. Finally, in [39] a rigorous foundation for integrating heterogeneous information is provided, by unifying information flow theory, institutions, formal concept analysis, and category theory.

By using a category theoretic language, ontologies can be represented as categories with finite limits and finite coproducts, where classes (concepts) are represented by nodes and functional relationships by arrows of a directed graph [40], and if an ontology has a representation by a category, then one may apply homological and homotopical algebra constructions to study the ontology [41]. Another view of the category theoretic perspective of ontologies and their underlying classes (concepts) is given in [42], where an ontology is regarded as a mathematical category of theories and a concept is represented by the ideas of theories and models that are borrowed from FCA. Moreover, in [43] an ontology can be described by formal concepts and thus it can be viewed as a category.

6. From the Yoneda Embedding to Formal Concepts

Our main point is the fact that, from an ontological point of view, the formal determination of a concept is guided by the interconnection existing between a concluding remark of the Yoneda embedding lemma of category theory and the intents of the formal concepts of FCA. In order to illustrate this point, an example is used in this section, relying on the assumption that attributes can also be considered as concepts, according to the German standard DIN 2330, stating that attributes “are units of thought which are gained by abstraction, and hence they are also concepts” [19, 44].

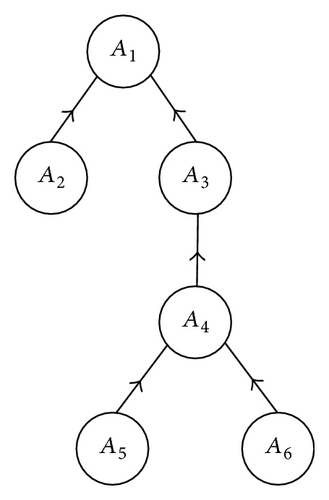
Following this statement, we can represent binary relations between entities within an ontology, by using a suitable formal context. For this purpose, we consider the entities of the ontology, both as objects and as attributes of the context. A binary relation present in the context signifies that the respective entities are related. As an example, the ontology of Figure 11, where the concepts A_i, i = 1, 2, … , 6, are hierarchically structured, is represented by the formal context of Figure 12, by using Lattice Miner [45], which is a formal concept analysis software tool for the construction of concept lattices.

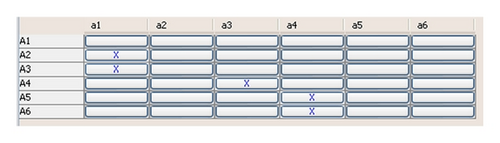
In Figure 12, the concept lattice and the formal concepts associated with the formal context of Figure 11 are depicted. It is a representation of a formal context called cross-table. The context has six attributes, a_i, i = 1, 2, … , 6. An “x” in a particular location or cell in the cross-table indicates that an object has an attribute, so, for example, the object “A₂” has the attribute “a₁.” Conversely a blank location indicates that the object does not have that attribute.

The concept lattice of Figure 13 contains five concepts, the most general being 〈{A₁, …, A₆}〉. The bottom concept is 〈{ }, {a₁, …, a₆}〉 because it is the concept of objects that have all attributes. The remaining concepts are marked with their intent and their extent.

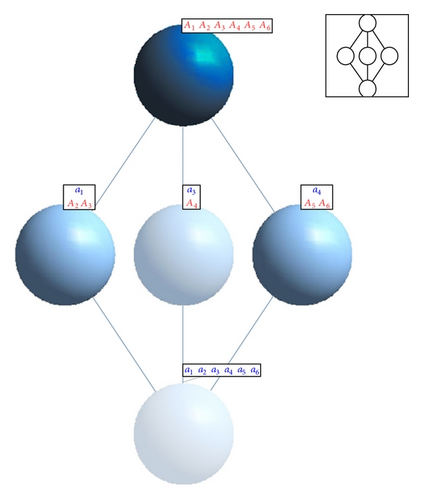
The diagram shows that there is an ordering over the concepts, which is a specialization ordering, denoted by ≤ [46].

It is interesting to notice here that the formal concepts represent the incoming relations to an ontology entity; that is, the intents of each formal concept correspond to the incoming arrows to each respective ontological concept. For example, the formal concept 〈{a₁}, {A₂, A₃}〉 represents the incoming relations (arrows) to ontological entity (concept) A₁. Now, if we consider a categorical perspective of the ontology, where the ontology entities are the objects of a category and the relations between the entities are the morphisms (arrows), then the intent of a formal concept represents the incoming arrows to an entity (object). But, from a category theoretic point of view, this remark is equivalent to the remark concluded from the Yoneda embedding lemma, which states that an object is completely determined by the incoming arrows to this object.

This statement yields from the Yoneda lemma, which is interpreted as follows: an object X of a category C is determined by the network of relationships that the object X has with all the other objects in C [47]. Thus, a concept can be clearly specified only by identifying the set of all its attributes and a set of attributes that are common for a concept determines completely a concept. This reciprocal condition can guide the building of the ontological status of concepts completely and consistently, since it eliminates polysemy and synonymy.

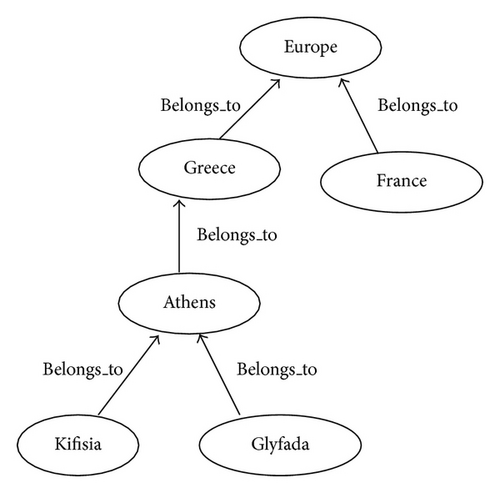
In a more illustrative example, such as that of the ontology of Figure 14, following the same process and taking into account its category theoretical representation, where concepts are objects of a category and their attributes/relations are morphisms, we observe the alignment between the intent of the formal concept 〈{belongs_To}, {Greece, France}〉 and the incoming arrows to the ontological entity “Europe,” that is, the Yoneda philosophy in unequivocally determining concepts in ontology engineering.

7. Equivalent Points of FCA and Category Theory

In this section, we refer to the possible meeting points of FCA and category theory aiming at direct research into the critical path of formalizing tasks concerning ontology engineering and facilitating progress of the field.

Due to the fact that we focus on the abstract notion of concepts, as well as their formal representation, and not on strict mathematical objects, it is incongruous to talk about equality between different points of mathematical theories, rather than equivalence, or isomorphism between them. Thus, the main question to be answered is not if two concepts are equivalent, but if they are isomorphic, that is, if they are interchangeable in the sense that they have the same relationships with all concepts within a context. In that sense, it will be interesting to investigate the correspondence between the basic notions and constructions of FCA and category theory, such as between (a) the supremum of any collection of formal concepts of a complete lattice and the initial object of a category, (b) the infimum of any collection of formal concepts of a complete lattice and the terminal object of a category, and (c) the application of the concept-forming operators to the intention or to the extension of a formal context and the fact that from an object of a category, one can define a specific functor that encodes the essence of these objects, as well as between other notions.

8. Conclusion

A formal view on ontologies or on ontological concepts can contribute a lot to the direction of achieving effective interoperability, since the coexistence of multiple heterogeneous ontologies within or among ontology-based applications is an objective reality. Thus, by carefully studying FCA and category theory, as the mathematical theories that provide frameworks for structuring, analyzing, and visualizing data to make them more understandable and for combining and maintaining heterogeneous collections of data to enable them to interoperate, respectively, we investigate some equivalent notions of both theories. This can lead, despite the abstract but quite accurate techniques of these theories, to create a unified framework for the ontological representation as well as their management.

Acknowledgments

The authors are indebted to the editor and the anonymous reviewers for their valuable suggestions and comments that greatly contributed to improving the paper.

References

1 Gruber T. R., Toward principles for the design of ontologies used for knowledge sharing, Formal Analysis in Conceptual Analysis and Knowledge Representation, 1993, Kluwer Academic/Plenum, New York, NY, USA.
Google Scholar
2 Borst W. N., Construction of Engineering Ontologies, Centre for Telematica and Information Technology, 1997, University of Tweenty, Ensschede, The Netherlands.
Google Scholar
3 Goguen J., F. Dan and M. Mungier, What is a concept?, 3596, Proceedings of the 13th Conference on Conceptual Structures, 2005, Springer, 52–77, Lecture Notes in Artificial Intelligence.
Google Scholar
4 Lambrechts L., Formal Concept Analysis, 2012, Vrije Universtiteit, Brussels, Belgium.
Google Scholar
5 Wille R., I. Rival, Restructuring lattice theory: an approach based on hierarchies of concepts, Ordered Sets, 1982, Reidel, Dordrecht, The Netherlands, 445–470.
Google Scholar
6 Bělohlávek R. and Sklenář V., Formal concept analysis over attributes with levels of granularity, Proceedings of the International Conference on Communicational Intelligence for Modelling, Control and Automation & Inter. Conf. on Intelligent Agents, Web Technologies and Internet Commerce, November 2005, Vienna, Austria.
Google Scholar
7 Bělohlávek R., Introduction to Formal Concept Analysis, 2008, UP Olomouc.
Google Scholar
8 Ganter B. and Will R., Formal Concept Analysis: Mathematical Foundations, 1999, Springer, Berlin, Germany.
Google Scholar
9 Awodey S., Category Theory, 2010, Oxford University Press, New York, NY, USA.
Google Scholar
10 Pierce B., Basic Category Theory for Computer Scientists, 1991, The MIT Press, Cambridge, Mass, USA.
Google Scholar
11 Lawvere W. and Schanuel S., Conceptual Mathematics, A First Introduction to Categories, 1997, Cambridge University Press, New York, NY, USA.
Google Scholar
12 Fiadeiro J., Categories for Software Engineering, 2004, Springer, New York, NY, USA.
Google Scholar
13 Obitko M., Snasel V., and Smid J., V. Snasel and R. Belohlavek, Ontology design with formal concept analysis, Proceedings of the International Conference on Concept Lattices and Their Applications (CLA ′04), 2004, 111–119.
Google Scholar
14 Priss U. E., Relational concept analysis: semantic structures in dictionaries and lexical databases [Dissertation], 1996, TH-Darmstadt.
Google Scholar
15 Huchard M., Hacene M. R., Roume C., and Valtchev P., Relational concept discovery in structured datasets, Annals of Mathematics and Artificial Intelligence. (2007) 49, no. 1–4, 39–76, 2-s2.0-34547651202, https://doi.org/10.1007/s10472-007-9056%2D3.
Google Scholar
16 Lehmann F. and Will R., A triadic approach to formal concept analysis, Conceptual Structures: Applications, Implementation and Theory, 1995, 954, Springer, Berlin, Germany, 32–43, Lecture Notes in Computer Science, https://doi.org/10.1007/3-540-60161-9_27.
Google Scholar
17 Konecny J. and Osicka P., M. kryszkiewicz and S. A. Obiedkov, General approach to triadic concept analysis, Proceedings of the 7th International Conference on Concept Lattices and Their Applications (CLA ′10), 2010, Sevilla, Spain, 116–126.
Google Scholar
18 Hitzler P., P. Valtchev and R. Jäschke, What′s happening in semantic web—and what FCA could have to do with it?, Formal Concept Analysis, 2011, 6628, Springer, Berlin, Germany, 18–23, Lecture Notes in Computer Science, https://doi.org/10.1007/978-3-642-20514-9_2.
Google Scholar
19 Cimiano P., Hotho A., Stumme G., and Tane J., Conceptual knowledge processing with formal concept analysis and ontologies, Proceedings of the 2nd International Conference on Formal Concept Analysis (ICFCA ′04), February 2004, 189–207, 2-s2.0-9444245010.
Google Scholar
20 Bendaoud R., Napoli A., and Toussaint Y., A. Gangemi and J. Euzenat, Formal concept analysis: a unified framework for building and refining ontologies, Knowledge Engineering: Practice and Patterns, 2008, 5268, Springer, Berlin, Germany, 156–171, Lecture Notes in Computer Science, https://doi.org/10.1007/978-3-540-87696-0_16.
Google Scholar
21 Nanda J., Simpson T. W., Kumara S. R. T., and Shooter S. B., A methodology for product family ontology development using formal concept analysis and web ontology language, Journal of Computing and Information Science in Engineering. (2006) 6, no. 2, 103–113, 2-s2.0-33745902837, https://doi.org/10.1115/1.2190237.
Google Scholar
22 Jurkevicius D. and Vasilecas O., Formal concept analysis for concept collecting and their analysis, Scientific Papers, University of Latvia, Computer Science and Information Technologies. (2009) 751, 22–39.
Google Scholar
23 Jäschke R., Hotho A., Schmitz C., Ganter B., and Stumme G., Discovering shared conceptualizations in folksonomies, Journal of Web Semantics. (2008) 6, no. 1, 38–53, 2-s2.0-44649173039, https://doi.org/10.1016/j.websem.2007.11.004.
Google Scholar
24 Rouane-Hacene M., Huchard M., Napoli A., and Valtchev P., Using formal concept analysis for discovering knowledge patterns, Proceedings of the 7th International Conference on Concept Lattices and Their Applications (CLA ′10), October 2010, Sevilla, Spain.
Google Scholar
25 Dolques X., Huchard M., Nebut C., and Saada H., Formal and relational concept analysis approaches in software engineering: an overview and an application to learn model transformation patterns in examples, Proceedings of the 1st ICESE Virtual Workshop on Software Engineering and Artificial Intelligence, 2011, Doha, Qatar.
Google Scholar
26 Healy M. J., R. Poli, M. Healy, and A. Kameas, Category Theory as a Mathematics for formalizing ontologies, Theory and Applications of Ontology: Computer Applications, 2010, Springer, New York, NY, USA, 487–510.
Google Scholar
27 Krötzsch M., Hitzler P., Ehrig M., and Sure Y., Category theory in ontology research: concrete gain from an abstract approach, 2005, AIFB, University of Karlsruhe.
Google Scholar
28 Brown R., Glazebrook J. F., and Baianu I. C., A conceptual construction of complexity levels theory in spacetime categorical ontology: non-abelian algebraic topology, many-valued logics and dynamic systems, Axiomathes. (2007) 17, no. 3-4, 409–493, 2-s2.0-37649005768, https://doi.org/10.1007/s10516-007-9010-3.
Google Scholar
29 Cafezeiro I. and Haueusler E. H., J. Grundy, S. Hartman, A. H. F. Laender, L. Maciaszek, and J. F. Roddick, Semantic interoperability via Category Theory, 83, Proceedings of the 26th International Conference on Conceptual Modeling, 2007, 197–202.
Google Scholar
30 Zimmermann A., Krötzsch M., Euzenat J., and Hitzler P., B. Bennett and C. Fellbaum, Formalizing ontology alignment and its operations with category theory, Proceedings of the International Conference on Formal Ontology in Information Systems (FOIS ′06), 2006, Baltimore, Md, USA, IOS Press, 277–288.
Google Scholar
31 Hitzler P., Krötzsch M., Ehrig M., and Sure Y., What is ontology merging? A category-theoretical perspective using pushouts, Proceedings of the 1st International Workshop on Contexts and Ontologies: Theory, Practice and Applications, July 2005, AAAI Press, 104–107, 2-s2.0-33646049021.
Google Scholar
32 Hu L. and Wang J., Geo-ontology integration based on category theory, Proceedings of the International Conference on Computer Design and Applications (ICCDA ′10), June 2010, Qinhuangdao, China, V15–V18, 2-s2.0-77955887333, https://doi.org/10.1109/ICCDA.2010.5540941.
Google Scholar
33 Goguen J. A. and Burstall R. M., Institutions: abstract model theory for specification and programming, Journal of the ACM. (1992) 39, no. 1, 95–146, 2-s2.0-0026444654, https://doi.org/10.1145/147508.147524.
Google Scholar
34 Mossakowski T., Maeder C., and Lüttich K., O. Grumberg and M. Huth, The heterogeneous tool set, Tools and Algorithms for the Construction and Analysis of Systems, 2007, 4424, Springer, Heidelberg, Germany, 519–522, Lecture Notes in Computer Science.
Google Scholar
35 Kutz O., Lücke D., and Mossakowski T., Heterogeneously structured ontologies: integration, connection and refinement, 90, Proceedings of the Knowledge Representation Ontology Workshop (KR ′08), 2008, Sydney, Australia, Conferences in Research and Practice in Information Technology.
Google Scholar
36 Barwise J. and Seligman J., Information Flow: The Logic of Distributed Systems, 1997, 44, Cambridge University Press, New York, NY, USA, Cambridge Tracts in Theoretical Computer Science.
Google Scholar
37 Kent R., The IFF foundation for ontological knowledge organization, Cataloging & Classification Quarterly. (2003) 37, no. 1-2, https://doi.org/10.1300/J104v37n01_13.
Google Scholar
38 Kalfoglou Y. and Schorlemmer M., The information flow approach to ontology-based semantic alignment, Theory and Applications of Ontology: Computer Applications, 2010, no. chapter 4, Springer, New York, NY, USA, 101–114.
Google Scholar
39 Goguen J., Information Integration in Institutions, L. Moss, Ed., 2004.
Google Scholar
40 Johnson M. and Rosebrugh R., R. Poli, M. Healy, and A. Kameas, Ontology engineering, universal algebra, and category theory, Theory and Applications of Ontology: Computer Applications, 2010, Springer, New York, NY, USA, 565–576.
Google Scholar
41 Glazunov N., Semantic web and category theory models, Proceedings of the International Seminar “iscrete Mathematics and its Applications”, 2007, Moscow, Russia, MGU, 309–311.
Google Scholar
42 Healy M. J. and Caudell T. P., Ontologies and worlds in category theory: implications for neural systems, Axiomathes. (2006) 16, no. 1-2, 165–214, 2-s2.0-33748860345, https://doi.org/10.1007/s10516-005-5474-1.
Google Scholar
43 Wendorff P., V. Gruhn, A formal approach to the assessment and improvement of terminological models used in information systems engineering, Proceedings of the 8th Eiropean Engineering Conference and 9th ACM SIGSOFT Symposium on the Foundations of Software Engineering (ESEC ′01 and FSE ′01), September 2001, Vienna, Australia, 83–87, 2-s2.0-0035783673.
Google Scholar
44 Deutsches Institut für Normung, Begriffe und Benennungen—Allgemeine Grundsätze, DIN, 1993, no. 2330.
Google Scholar
45 2012, http://lattice-miner.softpedia.com/.
Google Scholar
46 Tilley T., Concept Analysis and Formal Methods, 2000.
Google Scholar
47 Mazur B., B. Gold and R. Simons, When is one thing equal to other thing?, Proof and Other Dilemmas: Mathematics and Philosophy, 2007.
Google Scholar

Citing Literature

All articles

Yoneda Philosophy in Engineering

Abstract

1. Introduction

2. Formal Concept Analysis Background: Formal Context, Formal Concept, and Concept Lattice

3. Category Theory Background: Categories, Functors, Natural Transformations, and Yoneda Embedding Lemma

4. The Interplay between FCA and Ontological Concepts

5. The Interplay between Category Theory and Ontological Concepts

6. From the Yoneda Embedding to Formal Concepts

7. Equivalent Points of FCA and Category Theory

8. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Yoneda Philosophy in Engineering

Abstract

1. Introduction

2. Formal Concept Analysis Background: Formal Context, Formal Concept, and Concept Lattice

3. Category Theory Background: Categories, Functors, Natural Transformations, and Yoneda Embedding Lemma

4. The Interplay between FCA and Ontological Concepts

5. The Interplay between Category Theory and Ontological Concepts

6. From the Yoneda Embedding to Formal Concepts

7. Equivalent Points of FCA and Category Theory

8. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Related

Information