Advances in Tribology
Volume 2013, Issue 1 743987
Research Article
Open Access

Effect of Viscosity Variation on the Micropolar Fluid Squeeze Film Lubrication of a Short Journal Bearing

N. B. Naduvinamani, 

Corresponding Author

N. B. Naduvinamani

Department of Mathematics, Gulbarga University, Gulbarga 585 106, India kar.nic.in

Search for more papers by this author
Archana K. Kadadi, 

Archana K. Kadadi

Department of Mathematics, Gulbarga University, Gulbarga 585 106, India kar.nic.in

Search for more papers by this author
First published: 03 October 2013
https://doi.org/10.1155/2013/743987
Citations: 4
Academic Editor: Patrick De Baets

Abstract

A theoretical study of the effect of the viscosity variation on the squeeze film performance of a short journal bearing operating with micropolar fluid is presented. The modified Reynolds equation accounting for the viscosity variation in micropolar fluid is mathematically derived. To obtain a closed form solution, the short bearing approximation under constant load is considered. The modified Reynolds equation is solved for the fluid film pressure and then the bearing characteristics, such as obtaining the load carrying capacity and the squeeze film time. According to the results evaluated, the micropolar fluid as a lubricant improves the squeeze film characteristics and results in a longer bearing life, whereas the viscosity variation factor decreases the load carrying capacity and squeezes film time. The result is compared with the corresponding Newtonian case.

1. Introduction

The application of squeeze film action is commonly seen in gyroscopes, gears, aircraft engines, automotive engines, and the mechanics of synovial joints in human being and animals. The squeeze film behaviour arises from the phenomenon of two lubricated surfaces approaching each other with a normal viscosity. Because of the viscous lubricant present between the two surfaces, it takes certain time for these to come into contact. Since the viscous lubricant has a resistance to extrusion, a pressure is built up during that interval, and the lubricant film then supports the load. If the applied load acts for a short enough time, it may happen that the two lubricated surfaces will not meet at all. Therefore, the analysis of squeeze film action focuses on the load carrying and rate of approach.

The theory of micropolar fluids introduced by Eringen [1] deals with a class of fluid which exhibits certain microscopic effects arising from the local structures and micromotion of fluid elements. These fluids can support stress moments and body moments and are influenced by the spin inertia. A subclass of these fluids is the micropolar fluids which exhibit the microrotational effects and microrotational inertia. Eringen’s micropolar fluid theory defines the rotation vector called microrotation vector setting up of stress-strain rate constitutive equations.

The study of micropolar fluids has received considerable attention due to their applications in a number of processes that occur in industries such as extrusion of polymer fluids, solidification of liquid crystal, cooling of metallic plate in a bath, animal blood exotic lubricants, and colloidal and suspension solution. In the study of all these problems, the classical Navier-Stokes theory is inadequate, as the micropolar fluid theory is a subclass of microfluid theory and is obtained by imposing the skew symmetric properties of the gyration tensor in addition to a condition of microisotropy.

Several researchers [2–10] have studied the performance of different bearing systems lubricated with micropolar fluids and reported the advantages of these lubricants over Newtonian case such as increased load carrying capacity, lower coefficient of friction, and delayed time of approach. All these studies are based on the assumption that the viscosity is constant. However, in general, the viscosity of all liquids decreases with increasing temperature. Since lubricants are required to function over a wide range of temperatures, the realistic study of bearings must include the variation of viscosity with temperature. Yet, there is no accurate mathematical relation known to predict the variation of viscosity of lubricants with temperature. Hence, in the present paper, an attempt has been made to analyse the effects of variation of viscosity on the squeeze film lubrication of journal bearings lubricated with micropolar fluids. The following are the assumptions made in this paper.
  • (1)

    There exists a thermal equilibrium.

  • (2)

    The relationship for the variation of viscosity with temperature can be replaced by viscosity film thickness relation.

The second assumption is made on the basis of experimental validation [11] as the highest temperature occurs in the zones of minimum film thickness. Hence, the empirical relationship for the viscosity variation can be written as
()
where μ1 is the known viscosity at the film thickness h = h1 = c and Q lies between 0 to 1 according to the nature of the lubricant (Q = 0 for perfect Newtonian fluids and Q = 1 for perfect gases). The effects of viscosity variation due to lubricant additives in journal bearings were analysed by Sinha et al. [12] by employing the relation given in (1). The result is discussed by taking various numerical values for Q.

2. Mathematical Formulation of the Problem

The physical configuration of the journal bearing is shown in Figure 1. The shaft of radius r approaches the bearing surface with velocity V. The film thickness h is a function of θ, (h = c + ecos θ), where c is the radial clearance and e is the eccentricity of journal centre. The lubricant in the region is assumed to be micropolar fluid.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Squeeze film geometry of journal bearing.

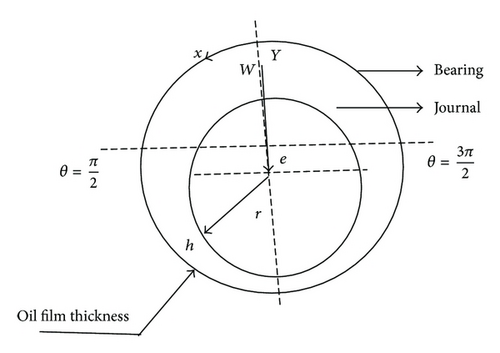
The constitutive equations for micropolar fluids proposed by Eringen [1] simplify considerably under the usual assumptions of hydrodynamic lubrication. The resulting equations under steady-state conditions are as follows.

Conservation of Linear Momentum
()
Conservation of Angular Momentum
()
Conservation of Mass
()
where (u, v, w) are the velocity components of the lubricant in the x, y, and z directions, respectively, (v1, v2, v3) are microrotational velocity components, χ is the spin viscosity, γ is the viscosity coefficient for micropolar fluids, and μ is the Newtonian viscosity coefficient.
The relevant boundary conditions are as follows:
  • (i)

    at the bearing surface (y = 0),

()
()
  • (ii)

    at the journal surface (y = h),

()
()

3. Solution of the Problem

The solution of (2) and (3) subject to the corresponding boundary conditions given in (5a), (5b), (6a), and (6b) is obtained as
()
()
()
()
where
()
where the symbols have their usual meaning as given in nomenclature.
The modified Reynolds equation is obtained by integrating the equation of continuity (4) with respect to y over the film thickness h and replacing u and w in (4) by their respective expressions given in (7) and (8) and also using the boundary conditions for v given in (5a) and (6a) in the form
()
where
()

3.1. Short Bearing Approximation

In order to simplify the problem and to obtain a closed form solution for the fluid film pressure, a short bearing approximation is made; the circumferential variations of pressure can be neglected as compared to the axial variation. Then the modified Reynolds equation (12) reduces to
()
Substituting μ = μ1(h/h1) Q in the above equation,
()
Integrating twice with respect to z and applying the following boundary conditions,
()
The fluid film pressure is given by
()
Introducing the nondimensional variables,
()
The nondimensional fluid film pressure is given in a closed form as
()
With the fluid film pressure known, the squeeze film characteristics such as load carrying capacity squeeze time can be evaluated.
The load carrying capacity is evaluated by integrating the squeeze film of action the negative pressure because the diverging film side is neglected. Consequently, the load carrying capacity of the bearing operating under steady load is given as
()
Introducing the nondimensional quantity,
()
The load carrying capacity can be expressed in nondimensional form as
()

The nondimensional load carrying capacity in (22) cannot be obtained by direct integration. It can be numerically evaluated by the method of Gaussian quadrature.

For constant load , the time taken by the journal centre to move from ε = 0 to ε = ε1 can be obtained by integrating (21) with respect to time.

Introducing the nondimensional response time,
()
The velocity of the journal centre can be expressed as
()
Equation (24) is a first-order nonlinear differential equation, with the initial condition
()
The above differential equation can be solved using Fourth-Order Runge-Kutta method. In the limiting case, as χ tends to zero, N → 0, the squeeze film characteristics obtained in (19), (22), and (24) reduce to their Newtonian counterparts obtained by [7].

4. Result and Discussion

The squeeze film lubrication of short journal bearings lubricated with Eringen’s micropolar fluid is analysed by considering the viscosity variations. The results are analysed with respect to various nondimensional parameters such as the coupling number, N, the additives length size parameter, , and the exponent Q of the viscosity variation. The coupling number N characterizes the coupling of linear and rotational motion arising due to microrotation of fluid molecules/additives in the lubricant. Thus, N signifies the coupling between the Newtonian and rotational viscosity. The parameter l has the dimension of length, and it can be identified as some property of fluid which depends on the size of the molecules such as the chain length of the polar additives in the lubricant. The effects of micropolar are expected to be dominant either when the characteristic material length is small or when the radial clearance is large; hence, . As Q → 0, the results of constant viscosity studied by [8] will be recovered. The following range of parameters is used for the discussion of the squeeze film characteristics:
()

4.1. Squeeze Film Pressure

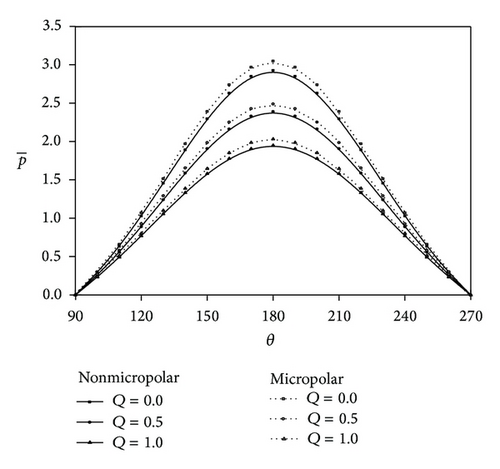
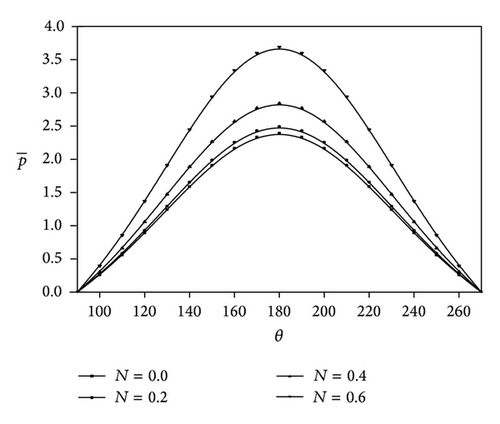
The variation of nondimensional squeeze film pressure with the angular coordinate θ for various values of Q is depicted in Figure 2. The dotted curves indicate the results of Newtonian case. It is observed that decreases for the increasing values of Q. Figure 3 depicts the variation of with θ for different values of N with and l = 0.4 and for the fixed values of Q = 0.5, ε = 0.2, and λ = 0.5. It is observed that increases for the increasing values of the coupling number N and the microstructure size parameter .

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Variation of nondimensional pressure with θ for different values of Q with , N  =  0.2, λ =  0.5, and ε = 0.2.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Variation of nondimensional with θ for different values of N with , Q  =  0.5, ε = 0.2, and λ = 0.5.

4.2. Load Carrying Capacity

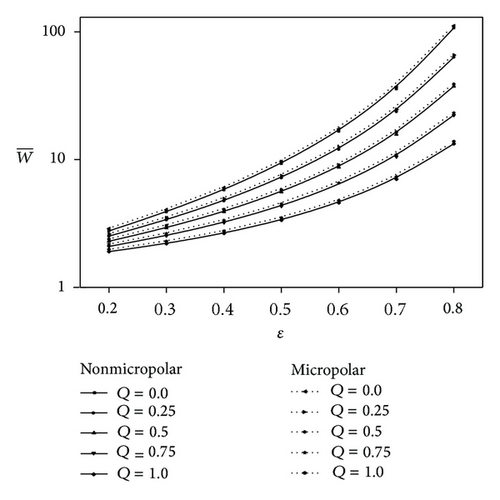
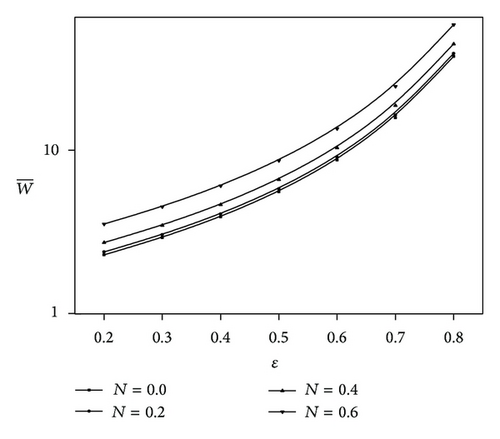
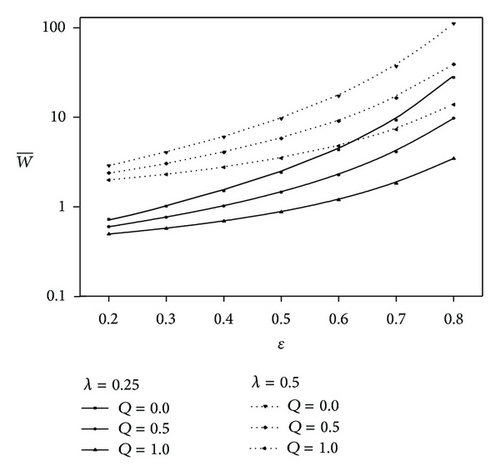
The variation of nondimensional load carrying capacity with the eccentricity ratio parameter ε is shown in the Figure 4 for various values of Q. It is observed that increases for increasing values of ε and decreases for increasing values of Q. Figure 5 shows the variation of with ε for different values of N and two values of (0, 0.4). It is clear that the effect of microstructure additives in the lubricant is to enhance the load carrying capacity as compared to the corresponding Newtonian case. An increase of nearly 4.16% in is observed at ε = 0.8 when , N = 0.2, Q = 0.5, and λ = 0.5. The effect of aspect ratio λ on the variation of with ε for different values of Q is shown in Figure 6. It is observed that when increases λ increases.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Variation of nondimensional load with ε for different values of Q with , N  =  0 .2, and λ =  0.5.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Variation of nondimensional load with ε for different values of N with , λ = 0.5, and Q = 0.5.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Variation of nondimensional load with ε for different values of Q with , λ = (0.5,0.25), and N = 0.2.

4.3. Squeeze Film Time

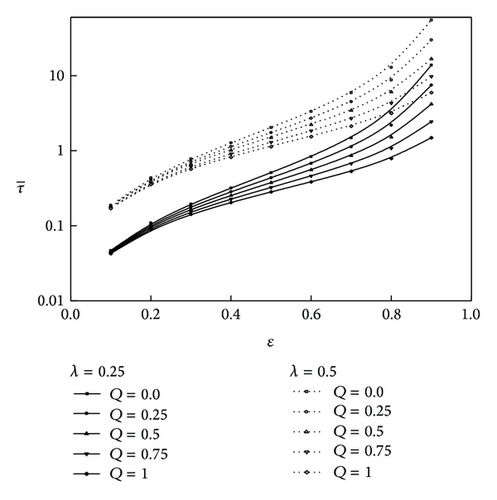
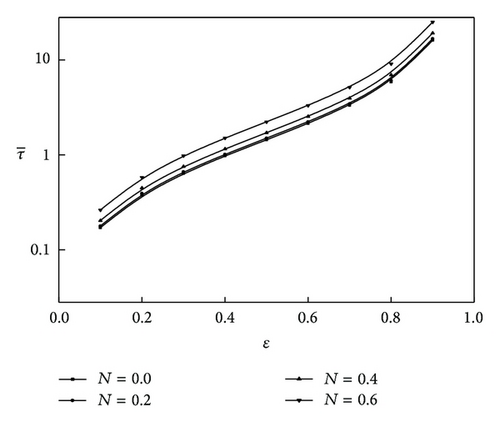
In Figure 7,  ε depicts the variation of nondimensional squeeze film time as a function of ε for different values of Q and for two values of the aspect ratio parameter λ with and N = 0.2. It is observed that decreases for the increasing value of Q. The effect of coupling number on the variation of with ε is depicted in the Figure 8 for and . it is observed that increases for the increasing values of N and . Hence, the effect of micropolar lubricants is to increase the load carrying capacity and squeeze film time as compared to the corresponding Newtonian case by which the performance of squeeze film in journal bearings improves.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Variation of nondimensional time with eccentricity ratio ε for different values of Q with , N = 0.2, and λ = (0.25,0.5).
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Varition of nondimensional time with eccentricity ratio ε for different values of N with , Q = 0.5, and λ = 0.5.

5. Conclusions

The effect of viscosity variations due to lubricant additives in the pure squeeze films in short journal bearing is analysed on the basis of the results presented in Figures 2–7; the following conclusions can be drawn.
  • (1)

    The effect of variation in viscosity is to decrease the load carrying capacity and squeeze film time.

  • (2)

    The presence of microstructures present in the lubricant enhances the load carrying capacity and lengthens the squeeze film time as compared to the corresponding Newtonian case.

Nomenclature

  • c:
  • Radial clearance
  • e:
  • Eccentricity
  • h:
  • Film thickness (h = c + ecos θ)
  • :
  • Nondimensional film thickness ( = h/c)
  • l:
  • Characteristic length of the polar suspension ( = (γ/4μ)1/2)
  • :
  • Nondimensional form of l  ( = l/c)
  • L:
  • Bearing length
  • N:
  • Coupling number ( = (χ/(χ+2μ))1/2)
  • p:
  • Lubricant pressure
  • :
  • Nondimensional pressure ( = pc2/μ1R2(∂ε/∂t))
  • Q:
  • Viscosity variation parameter
  • r:
  • Radius of the journal
  • t:
  • Squeezing time
  • u, v, w:
  • Components of fluid velocity in x, y, and z directions, respectively
  • v1, v2, v3:
  • Microrotational velocity components in the x, y, and z directions
  • V:
  • Squeeze velocity, (∂h/∂t)( = c(∂ε/∂t)cos θ)
  • W:
  • Load carrying capacity
  • :
  • Nondimensional load carrying capacity ( = Wc2/μLR3(∂ε/∂t))
  • x, y, z:
  • Cartesian coordinates
  • ε:
  • Eccentricity ratio ( = e/c)
  • χ:
  • Spin viscosity
  • γ:
  • Viscosity coefficient for micropolar fluids
  • μ:
  • Classical viscosity coefficient
  • μ1:
  • Inlet viscosity coefficient
  • λ:
  • Length to diameter ratio
  • τ:
  • Dimensionless response time
  • θ:
  • Circumferential coordinate.

      • The full text of this article hosted at iucr.org is unavailable due to technical difficulties.