Volume 2013, Issue 1 738653

Research Article

Open Access

BIBO Stability Analysis for Delay Switched Systems with Nonlinear Perturbation

Jincheng Wei,

Jincheng Wei

School of Electrical and Information Engineering, Xihua University, Chengdu 610096, China xhu.edu.cn

Search for more papers by this author

Peng Shi,

Peng Shi

College of Engineering and Science, Victoria University, Melbourne, VIC 8001, Australia vu.edu.au

School of Electrical and Electronic Engineering, The University of Adelaide, Adelaide, SA 5005, Australia adelaide.edu.au

Search for more papers by this author

Hamid Reza Karimi,

Corresponding Author

Hamid Reza Karimi

[email protected]

orcid.org/0000-0001-7629-3266

Department of Engineering, Faculty of Engineering and Science, University of Agder, 4898 Grimstad, Norway uia.no

Search for more papers by this author

Bo Wang,

Bo Wang

School of Electrical and Information Engineering, Xihua University, Chengdu 610096, China xhu.edu.cn

Search for more papers by this author

Jincheng Wei,

Jincheng Wei

School of Electrical and Information Engineering, Xihua University, Chengdu 610096, China xhu.edu.cn

Search for more papers by this author

Peng Shi,

Peng Shi

College of Engineering and Science, Victoria University, Melbourne, VIC 8001, Australia vu.edu.au

School of Electrical and Electronic Engineering, The University of Adelaide, Adelaide, SA 5005, Australia adelaide.edu.au

Search for more papers by this author

Hamid Reza Karimi,

Corresponding Author

Hamid Reza Karimi

[email protected]

orcid.org/0000-0001-7629-3266

Department of Engineering, Faculty of Engineering and Science, University of Agder, 4898 Grimstad, Norway uia.no

Search for more papers by this author

Bo Wang,

Bo Wang

School of Electrical and Information Engineering, Xihua University, Chengdu 610096, China xhu.edu.cn

Search for more papers by this author

First published: 12 May 2013

https://doi.org/10.1155/2013/738653

Citations: 7

Academic Editor: Hongli Dong

Share a link

Email
Wechat
Bluesky

Abstract

The problem of bounded-input bounded-output (BIBO) stability is investigated for a class of delay switched systems with mixed time-varying discrete and constant neutral delays and nonlinear perturbation. Based on the Lyapunov-Krasovskii functional theory, new BIBO stabilization criteria are established in terms of delay-dependent linear matrix inequalities. The numerical simulation is carried out to demonstrate the effectiveness of the results obtained in the paper.

1. Introduction

Time delay is a source of instability and poor performance and appears in many dynamic systems, for example, biological systems, chemical systems, metallurgical processing systems, nuclear reactor systems, and electrical networks [1]. Since the existence of time delays may lead to oscillation, divergence, or instability, considerable effort has been devoted to this area. As an important system performance index, BIBO stability means that any bounded input yields a bounded output and can be considered in many aspects, such as the free system dynamics, the basic single or double loop modulators, and the issues connected with bilinear input/output maps. Consequently, bounded-input bounded-output (BIBO) stability analysis of dynamical systems has attracted many scholars’ attention. For instance, in [2], BIBO stability criterion is derived for a three-dimensional fuzzy two-term control system, in [3], the problem on BIBO stabilization for a system with nonlinear perturbations is studied by discussing the existence of the positive definite solution to an auxiliary algebraic Riccati matrix equation, in [4], based on linear matrix inequality techniques, the stabilization criterion for uncertain time-delay system is presented to guarantee that bounded input can lead to bounded output, and in [5], BIBO stability for feedback control systems with time delay is studied through investigating the boundedness of the solutions for a class of nonlinear Volterra integral equations.

Recently, switched system becomes a research hotspot. Its motivation comes from the fact that many practical systems are inherently multimodal and the fact that some of intelligent control methods are based on the idea of switching between different controllers. Up till now, many investigations about stability of multiform switched systems have been carried out; see, for instance, [6–19] and references therein. Hence, it is our intention in this paper to tackle such an important yet challenging problem for BIBO stability analysis of delay switched systems. In addition, perturbations [20–26] and time delays [27–29] exist in many kinds of systems, and this makes the practical control problem complicated and has received much attention from scholars. Hence, in this paper, the BIBO stability for delay switched system with mixed time-varying discrete and constant neutral delays and nonlinear perturbation is concerned, and some original BIBO stability criteria are established in terms of linear matrix inequalities (LMIs). Finally, some simulation results are given to illustrate the effectiveness of our results. The main contributions of the paper are of two folds: (1) a delay-dependent technique is applied successfully into the analysis results process; (2) a Lyapunov-Krasovskii functional is constructed to derive a new form of the bounded real lemma (BRL) for the system under consideration.

The remainder of this paper is organized as follows. The model under consideration and some preliminaries are provided in Section 2. Section 3 presents the results on stability analysis. Section 4 gives an illustrative example. At last we conclude the paper in Section 5.

Notations used in this paper are fairly standard. Let Rⁿ be the n-dimensional Euclidean space, R^n×m represents the set of n × m real matrices, the symbol ^* denotes the elements below the main diagonal of a symmetric block matrix, A > 0 means that A is a real symmetric positive definitive matrix, and I denotes the identity matrix with appropriate dimensions. diag {⋯} denotes the diagonal matrix. E{·} refers to the expectation operator with respect to some probability measure P. ∥·∥ refers to the Euclidean vector norm or the induced matrix 2-norm. The superscript T stands for matrix transposition. L_n,h = L([−h, 0], Rⁿ) denotes the Banach space of continuous functions mapping the interval [−h, 0] into Rⁿ with the topology of uniform convergence.

2. Model Description and Preliminaries

First, consider the following delay switched system with nonlinear perturbation:

()

where x(t) ∈ Rⁿ is the state vector, d is the neutral delay, 0 ≤ τ(t) ≤ h is the time-varying discrete delay, φ(θ) ∈ L_n,h is the initial condition, σ(t) : [0, +∞) → M = {1,2, …, m} is the switching signal, u(t) ∈ R^l is the control input, Y(t) ∈ R^m is the system output, r(t) ∈ R^l is the reference input, and f(t) ∈ Rⁿ is the nonlinear time-varying perturbation, which satisfies ∥f(t, x(t))∥ ≤ β∥x(t)∥, where β is a positive scalar.

Model (1) can be represented as follows:

()

In this paper, the following well-known lemmas and definitions are needed.

Lemma 1 (see [30].)For any constant matrices E, G, and F with appropriate dimensions with F^TF ≤ kI, then

()

where x ∈ Rⁿ and y ∈ Rⁿand c and k are positive scalars.

Lemma 2 (see [31].)For any positive definite matrix Φ ∈ R^n×n, a positive scalar γ, and the vector function w : [0, γ] → Rⁿ such that the integrations concerned are well defined, then

()

Definition 3 (see [32].)A real-valued vector , if .

Definition 4 (see [32].)The control system with reference input r(t) is BIBO stable, if there exist some positive constants θ₁, θ₂, satisfying

()

for any reference input

Assumption 5. We assume that for system (1) there exist Hurwitz linear convex combinations of A_i; that is,

()

3. Main Results

In this section, we will establish some BIBO stability criteria using Lyapunov-Krasovskii functional theory and linear matrix inequalities.

Theorem 6. For given positive scalars h and k, switched system (1) is BIBO stable, if there exist ,,,,,, positive scalars ε, σ, matrices P₂, P₃, U, V, W, and symmetric positive definite matrices P, R, M, S, Q, satisfying

()

where

()

Proof. Since

()

there exist α_i ∈ [0,1], i = 1, …, m, satisfing

()

From (7), we can obtain

()

where

()

Let

()

We obtain

()

Construct a set as

()

We get

()

Construct the switching rule (SR): σ = i, for all

. The ith subsystem is activated when

. Choose the following Lyapunov-Krasovskii functional candidate:

()

with

()

where

()

The derivative of V(t) along the trajectory of the ith subsystem is given by

()

where

()

According to Leibniz-Newton formula, we have

()

From the obtained derivative terms in (21)–(26) and adding the left-hand side of (27) into (20), we obtain the following result:

()

where

()

When

, we can obtain

()

According to (7), we have

()

Hence,

()

Integrating the previous inequality from t₀ to t yields

()

Then, we have

()

Define

()

According to (17), we have

()

Hence, the following inequality can be concluded:

()

where

()

Then,

()

with

()

Therefore, switched system (1) is BIBO stable. This completes the proof.

4. Simulation Results

As an example, let us consider system (1) with the following parameters:

()

Remark 7. When the BIBO parameter k and the constant parameter β are given, the upper bound of time delay h of system (1) can be determined by solving the following optimization problem:

()

Now we consider the influence of parameters k and β on the maximal allowable delay in Tables 1 and 2.

Table 1. The maximal allowable delay for different parameters k when β is 0.1.

k = 0	k = 0.1	k = 0.2	k = 0.5
h_max = 3.3395	h_max = 2.5482	h_max = 2.1313	h_max = 1.5197

Table 2. The maximal allowable delay for different nonlinear parameters β when k is 0.1.

β = 0	β = 0.1	β = 0.2	β = 0.5
h_max = 2.6608	h_max = 2.5482	h_max = 2.4370	h_max = 2.1385

Remark 8. From Tables 1 and 2, it can be seen that the maximal allowable delay decreases with the rise of the parameter k and increases as the parameter β is reduced.

Then, we carry out some numerical simulation to verify the proposed methodology. The numerical simulation is with initial value φ(θ) = [−1.5; 1] ^T, t ∈ (−1.5,0), and following parameters

()

The switching signals are produced randomly with switching interval 0.2 seconds.

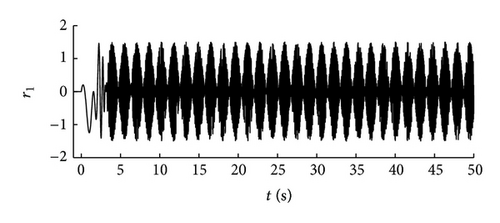
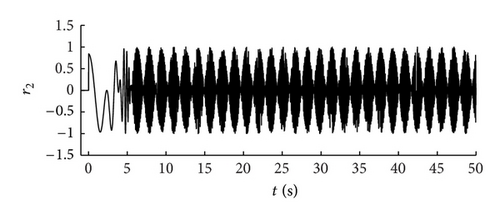
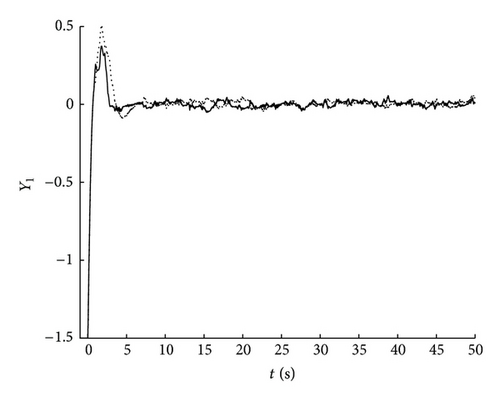
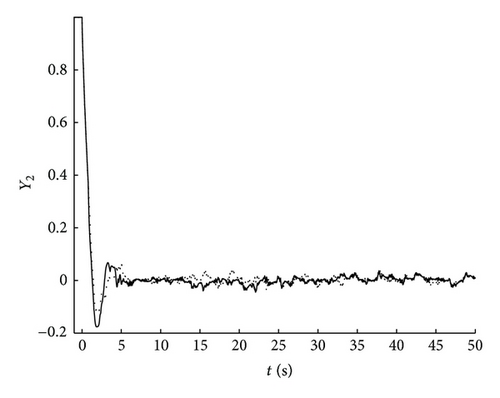
Remark 9. Figure 1 depicts the time response of system reference input variable r(t), and Figure 2 depicts the time response of switching signals. sw₁ denotes the switching signal added to the system for the first time, and sw₂ denotes the switching signal added to the system for the second time; Figure 3 depicts the time response of system output variable Y₁(t), and Figure 4 depicts the time response of system output variable Y₂(t). The solid line denotes the output variable of the switched system with the switching signal sw₁, and the dashed line denotes the output variable of the switched system with the switching signal sw₂. From the figures it can be seen that the system output jitters in a range with a given bounded input after a period of time, which means that the system is BIBO stable and demonstrates the effectiveness of our theoretical results.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Time response of the reference input variable r(t).

5. Conclusions

We have studied bounded-input bounded-output stability for a class of delay switched systems with nonlinear perturbation. Based on the Lyapunov-Krasovskii functional theory, new BIBO stabilization criteria were established in terms of delay-dependent linear matrix inequalities. Some numerical simulations have been conducted to demonstrate the effectiveness of the theoretical results obtained in this paper. Future work will investigate fault detection for delay switched systems.

Acknowledgments

This work was partially supported by the Key Projects of Xihua University (Z1120946), the National Key Basic Research Program, China (2012CB215202), the 111 Project (B12018), and the National Natural Science Foundation of China (61174058 and 61134001).

References

1 Kolmanovskiĭ V. and Myshkis A., Applied Theory of Functional-Differential Equations, 1992, 85, Kluwer Academic, Dordrecht, The Netherlands, MR1256486.
10.1007/978-94-015-8084-7
Google Scholar
2 Zhang X., Li S., and Li H., Structure and BIBO stability of a three-dimensional fuzzy two-term control system, Mathematics and Computers in Simulation. (2010) 80, no. 10, 1985–2004, https://doi.org/10.1016/j.matcom.2010.02.009, MR2665314.
10.1016/j.matcom.2010.02.009
Web of Science® Google Scholar
3 Li P. and Zhong S.-M., BIBO stabilization for system with multiple mixed delays and nonlinear perturbations, Applied Mathematics and Computation. (2008) 196, no. 1, 207–213, https://doi.org/10.1016/j.amc.2007.05.046, MR2382604.
10.1016/j.amc.2007.05.046
Web of Science® Google Scholar
4 Li P., Zhong S.-M., and Cui J.-Z., Delay-dependent robust BIBO stabilization of uncertain system via LMI approach, Chaos, Solitons and Fractals. (2009) 40, no. 2, 1021–1028, https://doi.org/10.1016/j.chaos.2007.08.059, MR2527843.
10.1016/j.chaos.2007.08.059
Web of Science® Google Scholar
5 Awwad E., Győri I., and Hartung F., BIBO stabilization of feedback control systems with time dependent delays, Applied Mathematics and Computation. (2012) 219, no. 8, 3664–3676, https://doi.org/10.1016/j.amc.2012.09.065, MR2996807.
10.1016/j.amc.2012.09.065
Web of Science® Google Scholar
6 Mahmoud M. and Shi P., Asynchronous H_∞ filtering of discrete-time switched systems, Signal Processing. (2012) 92, no. 10, 2356–2364.
10.1016/j.sigpro.2012.02.007
Web of Science® Google Scholar
7 Zhao X., Zhang L., Shi P., and Liu M., Stability of switched positive linear systems with average dwell time switching, Automatica. (2012) 48, no. 6, 1132–1137, https://doi.org/10.1016/j.automatica.2012.03.008, MR2917523.
10.1016/j.automatica.2012.03.008
Web of Science® Google Scholar
8 Zhao X., Zhang L., Shi P., and Liu M., Stability and stabilization of switched linear systems with mode-dependent average dwell time, IEEE Transactions on Automatic Control. (2012) 57, no. 7, 1809–1815, https://doi.org/10.1109/TAC.2011.2178629, MR2945945.
10.1109/TAC.2011.2178629
Web of Science® Google Scholar
9 Du D., Jiang B., and Shi P., Sensor fault estimation and compensation for time-delay switched systems, International Journal of Systems Science. (2012) 43, no. 4, 629–640, https://doi.org/10.1080/00207721.2010.517867, MR2889677.
10.1080/00207721.2010.517867
Web of Science® Google Scholar
10 Wu Z., Shi P., Su H., and Chu J., Delay-dependent stability analysis for switched neural networks with time-varying delay, IEEE Transactions on Systems, Man, and Cybernetics B. (2011) 41, no. 6, 1522–1530.
10.1109/TSMCB.2011.2157140
PubMed Web of Science® Google Scholar
11 Lian J., Feng Z., and Shi P., Observer design for switched recurrent neural networks: an average dwell time approach, IEEE Transactions on Neural Networks. (2011) 22, no. 10, 1547–1556.
10.1109/TNN.2011.2162111
PubMed Web of Science® Google Scholar
12 Wang D., Wang W., and Shi P., Delay-dependent model reduction for continuous-time switched state-delayed systems, International Journal of Adaptive Control and Signal Processing. (2011) 25, no. 9, 843–854, https://doi.org/10.1002/acs.1246, MR2837234.
10.1002/acs.1246
Web of Science® Google Scholar
13 Du D., Jiang B., and Shi P., Fault estimation and accommodation for switched systems with time-varying delay, International Journal of Control, Automation and Systems. (2011) 9, no. 3, 442–451.
10.1007/s12555-011-0303-3
Web of Science® Google Scholar
14 Ahn C. K. and Song M. K., L₂-L_∞ filtering for time-delayed switched hopfield neural networks, International Journal of Innovative Computing, Information and Control. (2011) 7, no. 4, 1831–1843, 2-s2.0-79952541604.
Web of Science® Google Scholar
15 Wu Z. G., Shi P., Su H., and Chu J., Delay-dependent exponential stability analysis for discrete-time switched neural networks with time-varying delay, Neurocomputing. (2011) 74, no. 10, 1626–1631, 2-s2.0-79954425822, https://doi.org/10.1016/j.neucom.2011.01.015.
10.1016/j.neucom.2011.01.015
Web of Science® Google Scholar
16 Zong G., Hou L., and Li J., A descriptor system approach to L₂-L_∞ filtering for uncertain discrete-time switched system with mode-dependent time-varying delays, International Journal of Innovative Computing, Information and Control. (2011) 7, no. 5A, 2213–2224, 2-s2.0-79956149569.
Web of Science® Google Scholar
17 Wang Y., Wang W., and Wang D., LMI approach to design fault detection filter for discrete-time switched systems with state delays, International Journal of Innovative Computing, Information and Control. (2010) 6, no. 1, 387–397, 2-s2.0-76549095061.
PubMed Web of Science® Google Scholar
18 Zhang L. and Jiang B., Stability of a class of switched linear systems with uncertainties and average dwell time switching, International Journal of Innovative Computing, Information and Control. (2010) 6, no. 2, 667–676, 2-s2.0-77649292084.
Web of Science® Google Scholar
19 Long F., Li C., and Cui C., Dynamic output feedback H_∞ control for a class of switched linear systems with exponential uncertainty, International Journal of Innovative Computing, Information and Control. (2010) 6, no. 4, 1727–1736, 2-s2.0-77951860599.
Web of Science® Google Scholar
20 Karimi H. R., Robust synchronization and fault detection of uncertain master-slave systems with mixed time-varying delays and nonlinear perturbations, International Journal of Control, Automation and Systems. (2011) 9, no. 4, 671–680.
10.1007/s12555-011-0408-8
Web of Science® Google Scholar
21 Karimi H. R., Adaptive H_∞ synchronization problem of uncertain master-slave systems with mixed time-varying delays and nonlinear perturbations: an LMI approach, International Journal of Automation and Computing. (2011) 8, no. 4, 381–390.
10.1007/s11633-011-0595-z
Google Scholar
22 Shi P., Luan X., and Liu F., H_∞ filtering for discrete-time systems with stochastic incomplete measurement and mixed delays, IEEE Transactions on Industrial Electronics. (2012) 59, 2732–2739.
10.1109/TIE.2011.2167894
Web of Science® Google Scholar
23 Karimi H. R., Zapateiro M., and Luo N., Stability analysis and control synthesis of neutral systems with time-varying delays and nonlinear uncertainties, Chaos, Solitons and Fractals. (2009) 42, no. 1, 595–603, https://doi.org/10.1016/j.chaos.2009.01.028, MR2543060.
10.1016/j.chaos.2009.01.028
Web of Science® Google Scholar
24 Basin M., Shi P., and Soto P., Central suboptimal H_∞ filtering for nonlinear polynomial systems with multiplicative noise, Journal of the Franklin Institute. (2010) 347, no. 9, 1740–1754, https://doi.org/10.1016/j.jfranklin.2010.08.006, MR2729483.
10.1016/j.jfranklin.2010.08.006
Web of Science® Google Scholar
25 Karimi H. R., Luo N., Zapateiro M., and Zhang L., H_∞ control design for building structures under seismic motion with wireless communication, International Journal of Innovative Computing, Information and Control. (2011) 7, 5269–5284.
Web of Science® Google Scholar
26 Karimi H. R., A sliding mode approach to H_∞ synchronization of master-slave time-delay systems with Markovian jumping parameters and nonlinear uncertainties, Journal of the Franklin Institute. Engineering and Applied Mathematics. (2012) 349, no. 4, 1480–1496, https://doi.org/10.1016/j.jfranklin.2011.09.015, MR2909498.
10.1016/j.jfranklin.2011.09.015
Web of Science® Google Scholar
27 Li X. and Gao H., A new model transformation of discrete-time systems with time-varying delay and its application to stability analysis, IEEE Transactions on Automatic Control. (2011) 56, no. 9, 2172–2178, https://doi.org/10.1109/TAC.2011.2146850, MR2865776.
10.1109/TAC.2011.2146850
Web of Science® Google Scholar
28 Li X., Gao H., and Yu X., A unified approach to the stability of generalized static neural networks with linear fractional uncertainties and delays, IEEE Transactions on System, Man, and Cybernetics B. (2011) 41, no. 5, 1275–1286.
10.1109/TSMCB.2011.2125950
PubMed Web of Science® Google Scholar
29 Gao H. and Li X., H_∞ filtering for discrete-time state-delayed systems with finite frequency specifications, IEEE Transactions on Automatic Control. (2011) 56, no. 12, 2935–2941, https://doi.org/10.1109/TAC.2011.2159909, MR2906681.
10.1109/TAC.2011.2159909
Web of Science® Google Scholar
30 Boyd S., El Ghaoui L., Feron E., and Balakrishnan V., Linear Matrix Inequalities in System and Control Theory, 1994, 15, Society for Industrial and Applied Mathematics, Philadelphia, Pa, USA, https://doi.org/10.1137/1.9781611970777, MR1284712.
10.1137/1.9781611970777
Google Scholar
31 Gu K., An integral inequality in the stability problem of time-delay systems, Proceedings of the 39th IEEE Confernce on Decision and Control, December 2000, Sydney, Australia, 2805–2810, 2-s2.0-0034439996.
Google Scholar
32 Wu H. S. and Mizukami K., Robust stabilization of uncertain linear dynamical systems, International Journal of Systems Science. (1993) 24, no. 2, 265–276, https://doi.org/10.1080/00207729308949487, MR1205273.
10.1080/00207729308949487
Web of Science® Google Scholar

Citing Literature

All articles

BIBO Stability Analysis for Delay Switched Systems with Nonlinear Perturbation

Abstract

1. Introduction

2. Model Description and Preliminaries

3. Main Results

4. Simulation Results

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

BIBO Stability Analysis for Delay Switched Systems with Nonlinear Perturbation

Abstract

1. Introduction

2. Model Description and Preliminaries

3. Main Results

4. Simulation Results

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information