Abstract and Applied Analysis
Volume 2013, Issue 1 735128
Research Article
Open Access

A Numerical Method for Fuzzy Differential Equations and Hybrid Fuzzy Differential Equations

K. Ivaz, 

K. Ivaz

Islamic Azad University, Shabestar Branch, Shabestar 5381637181, Iran iau.ac.ir

Department of Applied Mathematics, University of Tabriz, Tabriz 5166616471, Iran tabrizu.ac.ir

Search for more papers by this author
A. Khastan, 

Corresponding Author

A. Khastan

Mathematics Department, Institute for Advanced Studies in Basic Sciences, Zanjan 45137-66731, Iran iasbs.ac.ir

Search for more papers by this author
Juan J. Nieto, 

Juan J. Nieto

Departamento de Análisis Matemático, Facultad de Matemáticas, Universidad de Santiago de Compostela (USC), 15782 Santiago de Compostela, Spain usc.es

Department of Mathematics, Faculty of Science, King Abdulaziz University, P.O. Box 80203, Jeddah 21589, Saudi Arabia kau.edu.sa

Search for more papers by this author
First published: 08 October 2013
https://doi.org/10.1155/2013/735128
Citations: 8
Academic Editor: Marcia Federson

Abstract

Numerical algorithms for solving first-order fuzzy differential equations and hybrid fuzzy differential equations have been investigated. Sufficient conditions for stability and convergence of the proposed algorithms are given, and their applicability is illustrated with some examples.

1. Introduction

Hybrid systems are devoted to modeling, design, and validation of interactive systems of computer programs and continuous systems. That is, control systems that are capable of controlling complex systems which have discrete event dynamics as well as continuous time dynamics can be modeled by hybrid systems. The differential systems containing fuzzy valued functions and interaction with a discrete time controller are named hybrid fuzzy differential systems.

The Hukuhara derivative of a fuzzy-number-valued function was introduced in [1]. Under this setting, the existence and uniqueness of the solution of a fuzzy differential equation are studied by Kaleva [2, 3], Seikkala [4], and Kloeden [5]. This approach has the disadvantage that it leads to solutions which have an increasing length of their support [2]. A generalized differentiability was studied in [6–8]. This concept allows us to resolve the previously mentioned shortcoming. Indeed, the generalized derivative is defined for a larger class of fuzzy-number-valued functions than the Hukuhara derivative. Some applications of numerical methods in FDE and hybrid fuzzy differential equation (HFDE) are presented in [9–19]. Some other approaches to study FDE and fuzzy dynamical systems have been investigated in [20–22].

In engineering and physical problems, Trapezoidal rule is a simple and powerful method to solve numerically related ODEs. Trapezoidal rule has a higher convergence order in comparison to other one step methods, for instance, Euler method.

In this work, we concentrate on numerical procedure for solving FDEs and HFDEs, whenever these equations possess unique fuzzy solutions.

In Section 2, we briefly present the basic definitions. Trapezoidal rule for solving fuzzy differential equations is introduced in Section 3, and convergence and stability of the mentioned method are proved. The proposed algorithm is illustrated by solving two examples. In Section 4 we present Trapezoidal rule for solving hybrid fuzzy differential equations.

2. Preliminary Notes

In this section the most basic definition of ordinary differential equations (ODEs) and notation used in fuzzy calculus are introduced. See, for example, [23].

Consider the first-order ordinary differential equation
()
where f : [t0, tN] × ℝn → ℝn and t0 ∈ ℝ. A linear multistep method applied to (1) is
()
with αi, βi ∈ ℝ, αk ≠ 0, given starting values y0, y1, …, yk−1. In the case βk = 0, the corresponding methods (2) are explicit and are implicit otherwise. The constant step size h > 0 leads to time discretizations with respect to the grid points tm : = t0 + mh. The value ym+i is an approximation of the exact solution at tm+i. The special case of explicit methods, m = 2, α0 = −1, α1 = 0, α2 = 1, β0 = β2 = 0, and β1 = 2, corresponds to the Midpoint rule:
()
and the especial case of implicit methods, m = 1, α0 = −1, α1 = 1, and β0 = β1 = 1/2, corresponds to the Trapezoidal rule:
()
For an explicit method, (2) yields the current value ym+k directly in terms of ym+j, fm+j, j = 0,1, …, k − 1, which, at this stage of the computation, have already been calculated. An implicit method will call for the solution, at each stage of computation, of the the equation
()
where g is a known function of previously calculated values ym+j, fm+j, j = 0,1, …, k − 1. When the original differential equation in (1) is linear, then (5) is linear in ym+k, and there is no problem in solving it. When f is nonlinear, for finding solution of (1), we can use the following iteration:
()

Definition 1. Associated with the multistep method (2), we define the first characteristic polynomial as follows:

()

Theorem 2. A multistep method is stable if the first characteristic polynomial satisfies the root condition, that is, the roots of ρ(ξ) lie on or within the unit circle, and further the roots on the unit circle are simple.

According to Theorem 2, we know the Midpoint rule and Trapezoidal rule are stable.

Definition 3. The difference operator

()
and the associated linear multistep method (2) are said to be of order p if for the following equation:
()
we have C0 = C1 = ⋯ = Cp = 0, Cp+1 ≠ 0, where and , for i ≥ 1.

According to Definition 3, Midpoint rule and Trapezoidal rule are second-order methods.

We now recall some general concepts of fuzzy set theory; see, for example, [2, 24].

Definition 4. Let X be a nonempty set. A fuzzy set u in X is characterized by its membership function  u : X → [0,1], and u(x) is interpreted as the degree of membership of an element x in fuzzy set u for each x ∈ X.

Let us denote by ℝF the class of fuzzy subsets of the real axis, that is,
()
satisfying the following properties:
  • (i)

    u  is normal, that is, there exists s0 ∈ ℝ such that u(s0) = 1,

  • (ii)

    u is a convex fuzzy set (i.e., u(ts + (1 − t)r) ≥ min  {u(s), u(r)}, ∀t ∈ [0,1],   s, r ∈ ℝ),

  • (iii)

    u is upper semicontinuous on ℝ,

  • (iv)

    cl {s ∈ ℝ∣u(s) > 0} is compact, where cl  denotes the closure of a subset.

The space ℝF is called the space of fuzzy numbers. Obviously, ℝ ⊂ ℝF. For 0 < α ≤ 1, we denote
()
Then from (i)–(iv), it follows that the α-level set [u] α is a nonempty compact interval for all 0 ≤ α ≤ 1. The notation
()
denotes explicitly the α-level set of u. The following remark shows when is a valid α-level set.

Remark 5. The sufficient conditions for to define the parametric form of a fuzzy number are as follows:

  • (i)

    is a bounded monotonic increasing (nondecreasing) left-continuous function on (0,1] and right-continuous for α = 0,

  • (ii)

    is a bounded monotonic decreasing (nonincreasing) left-continuous function on (0,1] and right-continuous for α = 0.

  • (iii)

    , 0 ≤ α ≤ 1.

For u, v ∈ ℝF and λ ∈ ℝ, the sum u + v and the product λu are defined by [u + v] α = [u] α + [v] α, [λu] α = λ[u] α, ∀α ∈ [0,1], where [u] α + [v] α means the usual addition of two intervals (subsets) of ℝ, and λ[u] α means the usual product between a scaler and a subset of ℝ.

The metric structure is given by the Hausdorff distance
()
by
()
The following properties are well known:
  •  

    D(u + w, v + w) = D(u, v), ∀u, v, w ∈ ℝF,

  •  

    D(ku, kv) = |k|D(u, v), ∀k ∈ ℝ, u, v ∈ ℝF,

  •  

    D(u + v, w + e) ≤ D(u, w) + D(v, e), ∀u, v, w, e ∈ ℝF,

and (ℝF, D) is complete metric spaces.
Let I be a real interval. A mapping y : I → ℝF is called a fuzzy process and its α-level set is denoted by
()
A triangular fuzzy number N is defined by an ordered triple (xl, xc, xr) ∈ ℝ3 with xl ≤ xc ≤ xr, where the graph of N(s) is a triangle with base on the interval [xl, xr] and vertex at s = xc. An α-level of N is always a closed, bounded interval. We write N = (xl, xc, xr); then
()
for any 0 ≤ α ≤ 1.

Definition 6. Let x, y ∈ ℝF. If there exists z ∈ ℝF such that x = y + z, then z is called the H-difference of x and y, and it is denoted by x ⊖ y.

In this paper the sign “⊖” stands always for H-difference, and let us remark that x ⊖ y ≠ x + (−1)y. Usually we denote x + (−1)y by x − y, while x ⊖ y stands for the H-difference.

Definition 7. Let F : I → ℝF be a fuzzy function. We say F is Hukuhara differentiable at t0 ∈ I if there exists an element F′(t0) ∈ ℝF such that the limits

()
exist and are equal to F′(t0). Here the limits are taken in the metric space (ℝF, D).

Definition 8. Let [a, b] ⊂ I. The fuzzy integral is defined by

()
provided the Lebesgue integrals on the right exist.

Remark 9. Let [a, b] ⊂ I. If F : I → ℝF is Hukuhara differentiable and its Hukuhara derivative F′ is integrable over [a, b], then

()
for all values of t0, t, where a ≤ t0 ≤ t ≤ b.

Theorem 10. Let (ti, ui), i = 0,1, …, n, be the observed data, and suppose that each of the is a triangular fuzzy number. Then for each t ∈ [t0, tn], the fuzzy polynomial interpolation is a fuzzy-value continuous function f : ℝ → ℝF, where f(ti) = ui,  f(t) = (fl(t), fc(t), fr(t)) ∈ ℝF, and

()
such that .

Proof. See [25].

3. Fuzzy Differential Equations

Consider the first-order fuzzy differential equation y′ = f(t, y), where y is a fuzzy function of t, f(t, y) is a fuzzy function of crisp variable t and fuzzy variable y, and y′ is Hukuhara fuzzy derivative of y. If an initial value y(t0) = y0 ∈ ℝF is given, a fuzzy Cauchy problem of first order will be obtained as follows:
()
By Theorem 5.2 in [11] we may replace (21) by equivalent system
()
The parametric form of (22) is given by
()
for 0 ≤ α ≤ 1. In some cases the system given by (23) can be solved analytically. In most cases analytical solutions may not be found, and a numerical approach must be considered. Some numerical methods such as the fuzzy Euler method, Nyström method, and predictor-corrector method presented in [7, 10, 11, 13, 15]. In the following, we present a new method to numerical solution of FDE.

3.1. Trapezoidal Rule for Fuzzy Differential Equations

In the interval I = [t0, T] we consider a set of discrete equally spaced grid points t0 < t1 < t2 < ⋯<tN = T. The exact and approximate solutions at tn, 0 ≤ n ≤ N, are denoted by and , respectively. The grid points at which the solution is calculated are
()
Let , 0 ≤ p < N which f(tp, yp) is triangular fuzzy number. We have
()
By fuzzy interpolation, Theorem 10, we get
()
()
()
where , interpolates f(t, y(t)) with the interpolation data given by the value f(tp, yp), and l0(t) = (t − tp+1)/(tp − tp+1), l1(t) = (t − tp)/(tp+1 − tp).
For tp ≤ t ≤ tp+1 we have
()
From (16) and (25) it follows that
()
where
()
()
According to (25), if (26) and (27) are situated in (31), (27) and (28) in (32), we obtain
()
By integration we have
()
By (16) deduce
()
Similarly we obtain
()
Therefore, Trapezoidal rule is obtained as follows:
()
for 0 ≤ p < N.

3.2. Convergence and Stability

Suppose the exact solution is approximated by some . The exact and approximate solutions at tn,   0 ≤ n ≤ N, are denoted by and , respectively. Our next result determines the pointwise convergence of the Trapezoidal approximates to the exact solution. The following lemma will be applied to show convergence of these approximates; that is,
()

Lemma 11. Let a sequence of numbers satisfy

()
for some given positive constant A and B. Then
()

Proof. See [15].

Let F(t, u, v) and G(t, u, v) be the functions F and G of (22), where u and v are constants and u ≤ v. The domain where F and G are defined is therefore
()

Theorem 12. Let F(t, u, v) and G(t, u, v) belong to C2(K), and let the partial derivatives of F, G be bounded over K. Then for arbitrary fixed α : 0 ≤ α ≤ 1, the Trapezoidal rule approximate of (37) converges to the exact solutions , uniformly in t, for .

Proof. It is sufficient to show that

()
By using Taylor’s theorem, we get
()
where , . Consequently,
()
Denote and . Then
()
()
where and , and L1, L2 > 0 is a bound for partial derivatives of F and G in tp, tp+1. Thus,
()
If we put |up| = |wp| + |vp| and L = max  {L1, L2} < 1/2h, then
()
Then by Lemma 11 and w0 = v0 = 0, we have
()
If h → 0, then wn → 0, vn → 0 which concludes the proof.

Remark 13. According to Definition 3, Trapezoidal rule is a second-order method. In fact we may consider the definition of convergence order given in Definition 3 for system of ODEs.

Theorem 14. Trapezoidal rule is stable.

Proof. For Trapezoidal rule exists only one characteristic polynomial ρ(ξ) = ξ − 1, and it is clear that satisfies the root condition. Then by Theorem 2, the Trapezoidal rule is stable.

3.3. Numerical Results

In this section we apply Trapezoidal rule for numerical solution of two linear fuzzy differential equations. We compare our results with Midpoint rule. The authors in [13] have presented the Midpoint rule for numerical solution of FDEs as follows:
()
The Midpoint rule is a second-order and stable method [13].

In the following two examples, the implicit nature of Trapezoidal rule for solving linear fuzzy differential equation is implemented by solving a linear system at each stage of computation.

Example 15 (see [13].)Consider the initial value problem

()
The exact solution at t = 0.1 for 0 ≤ α ≤ 1 is given by
()
A comparison between the exact solution, Y(t; α), and the approximate solutions by Midpoint method [13], yMid(t; α), and Trapezoidal method, y(t; α), at t = 0.1 with N = 10, is shown in Table 1 and Figure 1.

α
0 0.9636348 0.9686955 0.9636356 1.0188934 1.0138372 1.0188941
0.1 0.9677550 0.9723098 0.9677558 1.0174878 1.0129374 1.0174885
0.2 0.9718752 0.9759241 0.9718760 1.0160820 1.0120376 1.0160828
0.3 0.9759954 0.9795385 0.9759961 1.0146763 1.0111377 1.0146772
0.4 0.9801155 0.9831529 0.9801163 1.0132707 1.0102379 1.0132715
0.5 0.9842358 0.9867672 0.9842365 1.0118650 1.0093381 1.0118657
0.6 0.9883559 0.9903815 0.9883567 1.0104593 1.0084382 1.0104601
0.7 0.9924761 0.9939959 0.9924769 1.0090537 1.0075384 1.0090544
0.8 0.9965963 0.9976103 0.9965971 1.0076480 1.0066386 1.0076487
0.9 1.0007164 1.0012246 1.0007173 1.0062424 1.0057387 1.0062431
1 1.0048367 1.0048389 1.0048374 1.0048367 1.0048389 1.0048374
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
(-) Exact solution, (∘) Trapezoidal, and (+) Midpoint approximated points.

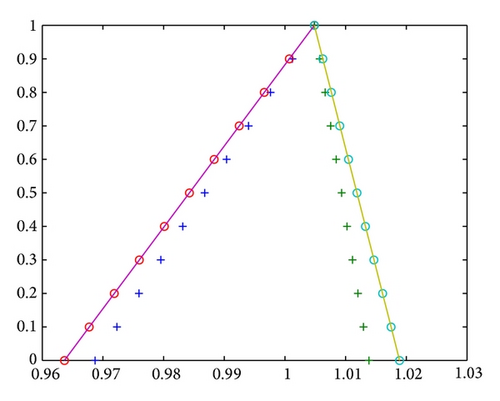
Example 16. Let us consider the first-order fuzzy differential equation

()
where y0 = [0.96 + 0.04α, 1.01 − 0.01α].

The exact solution at t = 0.1 is given by

()
A comparison between the exact solution, Y(t; α), and the approximate solutions by Midpoint method, yMid(t; α), and Trapezoidal method, y(t; α), at t = 0.1 with N = 10, is shown in Table 2 and Figure 2.

α
0 0.8636348 0.8686954 0.8636356 0.9188934 0.9138373 0.9188941
0.1 0.8677550 0.8723098 0.8677558 0.9174877 0.9129374 0.9174885
0.2 0.8718752 0.8759242 0.8718759 0.9160821 0.9120376 0.9160828
0.3 0.8759954 0.8795385 0.8759961 0.9146764 0.9111378 0.9146771
0.4 0.8801156 0.8831528 0.8801163 0.9132707 0.9102379 0.9132714
0.5 0.8842357 0.8867672 0.8842365 0.9118651 0.9093381 0.9118658
0.6 0.8883559 0.8903816 0.8883567 0.9104593 0.9084383 0.9104601
0.7 0.8924761 0.8939959 0.8924769 0.9090537 0.9075384 0.9090545
0.8 0.8965963 0.8976102 0.8965970 0.9076480 0.9066386 0.9076487
0.9 0.9007165 0.9012246 0.9007173 0.9062423 0.9057388 0.9062431
1 0.9048367 0.9048389 0.9048374 0.9048367 0.9048389 0.9048374
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
(-) Exact solution, (∘) Trapezoidal, and (+) Midpoint approximated points.

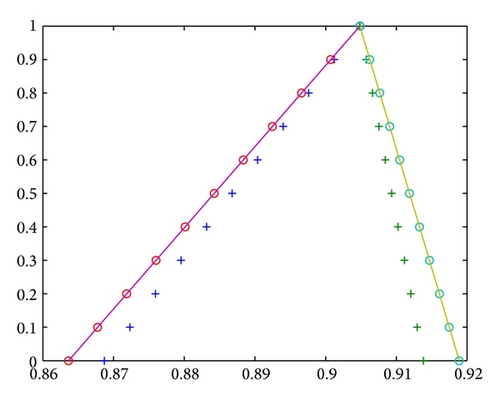
4. Hybrid Fuzzy Differential Equations

Consider the hybrid fuzzy differential equation
()
where is strictly increasing and unbounded, yk denotes y(tk), f : [t0, ∞) × ℝF × ℝF → ℝF is continuous, and each λk : ℝF → ℝF is a continuous function. A solution y to (55) will be a function y : [t0, ∞) → ℝF satisfying (55). For k = 0,1, 2, …, let fk : [tk, tk+1] × ℝF → ℝF, where fk(t, yk(t)) = f(t, y(t), λk(yk)). The hybrid fuzzy differential equation in (55) can be written in expanded form as
()
and a solution of (55) can be expressed as
()
We note that the solution y of (55) is continuous and piecewise differentiable over [t0, ∞) and differentiable on each interval (tk, tk+1) for any fixed yk ∈ ℝF and k = 0,1, 2, ….

Theorem 17. Suppose for k = 0,1, 2, … that each fk : [tk, tk+1] × ℝF → ℝF is such that

()
If for each k = 0,1, 2, … there exists Lk > 0 such that
()
for all α ∈ [0,1], then (55) and the hybrid system of ODEs
()
are equivalent.

Proof. See [19].

4.1. Trapezoidal Rule for Hybrid Fuzzy Differential Equations

For each α ∈ [0,1], to numerically solve (55) in [t0, t1], [t1, t2], …, [tk, tk+1], …, replace each interval [tk, tk+1], k = 0,1, … by a set of Nk+1 regularly spaced grid points (including the endpoints). The grid point on [tk, tk+1] will be tk,n = tk + nhk, hk = (tk+1 − tk)/Nk, 0 ≤ n ≤ Nk at which the exact solution will be approximated by some . We set , and , if k ≥ 1.

According to Section 3, by similar computation we obtain the Trapezoidal rule for solving (60) as follows:
()
for 0 ≤ n < Nk, k = 0,1, 2, ….

Next, we give the algorithm to numerically solve (55) in [t0, t1], [t1, t2], …, [tk, tk+1], ….

First Step. will be a numerical solution generated by (61) for k = 0 as follows:
()
is a numerical solution of (60) over [t0, t1].
Second Step. For each k ≥ 1, will be numerical solution generated by (61) for
()
where , is a numerical solution of (60) over [tk, tk+1] for each k ≥ 1.
For arbitrary fixed α ∈ [0,1] and k, we can prove that the numerical solution of (55) converges to the exact solution; that is,
()
The Trapezoidal rule is a one-step method as the Euler method. Therefore, the proof of the convergence closely follows the idea of the proof of Theorem 3.2 in [18] and Theorem 4.1 in [19].

Theorem 18. Consider the system of (55). Suppose for some fixed k and α ∈ [0,1] that , where 0 ≤ ni ≤ Ni is obtained by (61). Then

()

Proof. See [19].

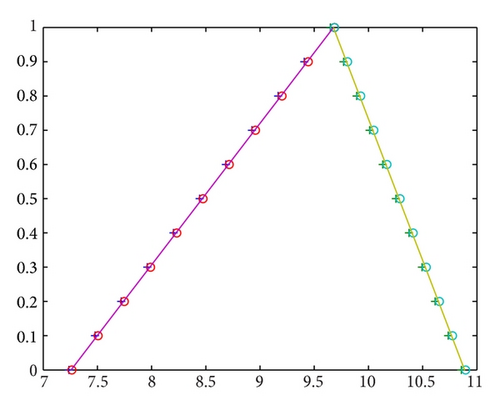
Example 19. Consider the following hybrid fuzzy system:

()
where γ is a triangular fuzzy number having α-level sets [γ] α = [0.75 + 0.25α, 1.125 − 0.125α],
()
By [19, Example 1], we know (66) has a unique solution and the exact solution on [0,2] is given by
()
To numerically solve the hybrid fuzzy initial value problem (66) we apply the Trapezoidal rule for hybrid fuzzy differential equations.

A comparison between the exact solution and the approximate solutions by Midpoint method and Trapezoidal method at t = 2 with N = 10 is shown in Table 3 and Figure 3.

α
0 7.2644238 7.2370696 7.2577319 10.8966360 10.8556042 10.8865976
0.1 7.5065713 7.4783049 7.4996562 10.7755623 10.7349863 10.7656355
0.1 7.7487187 7.7195406 7.7415805 10.6544886 10.6143684 10.6446733
0.1 7.9908662 7.9607763 7.9835048 10.5334148 10.4937506 10.5237112
0.1 8.2330141 8.2020121 8.2254295 10.4123411 10.3731327 10.4027491
0.1 8.4751616 8.4432478 8.4673538 10.2912674 10.2525148 10.2817869
0.1 8.7173090 8.6844835 8.7092781 10.1701937 10.1318970 10.1608248
0.1 8.9594564 8.9257193 8.9512024 10.0491199 10.0112791 10.0398626
0.1 9.2016039 9.1669550 9.1931267 9.9280462 9.8906612 9.9189005
0.1 9.4437513 9.4081898 9.4350510 9.8069725 9.7700434 9.7979374
1 9.6858988 9.6494255 9.6769753 9.6858988 9.6494255 9.6769753
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
(-) Exact solution, (∘) Trapezoidal, and (+) Midpoint approximated points.

5. Conclusion

We have presented Trapezoidal rule for numerical solution of first-order fuzzy differential equations and hybrid fuzzy differential equations. Also convergence and stability of the method are studied. To illustrate the efficiency of the new method, we have compared our method with the Midpoint rule in some examples. We have shown the global error in Trapezoidal rule is much less than in Midpoint rule.

For future research, we will apply Trapezoidal rule to fuzzy differential equations and hybrid fuzzy differential equations under generalized Hukuhara differentiability. Also one can apply Trapezoidal rule and Midpoint rule as a predictor-corrector method to solve FDE and HFDE.

Acknowledgments

The first author would like to thank the financial support of the Islamic Azad University, Shabestar Branch. The research of the third author has been partially supported by Ministerio de Economia y Competitividad (Spain), Project MTM2010-15314, and cofinanced by the European Community fund FEDER. This research was completed during the visit of the second author to the USC.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.