Single Peak Solitons for the Boussinesq-Like B(2,2) Equation
Abstract
The nonlinear dispersive Boussinesq-like B(2,2) equation , which exhibits single peak solitons, is investigated. Peakons, cuspons and smooth soliton solutions are obtained by setting the B(2,2) equation under inhomogeneous boundary condition. Asymptotic behavior and numerical simulations are provided for these three types of single peak soliton solutions of the B(2,2) equation.
1. Introduction
2. Asymptotic Behavior of Solutions
In this section, we first introduce some notations. Let Ck(Ω) denote the set of all k times continuously differential functions on the open set Ω. refers to the set of all functions whose restriction on any compact subset is Lp integrable. stands for .
Definition 1. A function u(x, t) = U(x − ct) is said to be a single peak soliton solution for the B(2,2) equation (3) if U(ξ) satisfies the following conditions.
- (A1)
U(ξ) is continuous on R and has a unique peak point ξ0, where u(ξ) attains its global maximum or minimum value.
- (A2)
U(ξ) ∈ C4(R − {ξ0}) satisfies (8) on R − {ξ0}.
- (A3)
limξ→±∞U(ξ) = A.
Definition 2. A wave function U is called peakon if U is smooth locally on either side of ξ0 and .
Definition 3. A wave function U is called cuspon if U is smooth locally on either side of ξ0 and .
Without any loss of generality, we choose the peak point ξ0 as vanishing, ξ0 = 0.
Theorem 4. Suppose that U(ξ) is a single peak soliton solution for the B(2,2) equation (3) at the peak point ξ0 = 0. Then one has the following.
- (i)
If A < −2c2/3, then U(0) = 0.
- (ii)
If A ≥ −2c2/3, then U(0) = 0 or U(0) = B1 or U(0) = B2.
Proof. If U(0) ≠ 0, then U(ξ) ≠ 0 for any ξ ∈ R since U(ξ) ∈ C4(R − {0}). Differentiating both sides of (9) yields U(ξ) ∈ C∞(R).
- (i)
For A < −2c2/3, if U(0) ≠ 0, then U ∈ C∞(R). By the definition of single peak soliton, we have U′(0) = 0. However, by (9) we must have U(0) = A, which contradicts the fact that 0 is the unique peak point.
- (ii)
For A ≥ −2c2/3, if U(0) ≠ 0, by (9) we know that U′(0) exists. According to the definition of peak point, we have U′(0) = 0. Thus we obtain U(0) = B1 or U(0) = B2 from (10) since U(0) = A contradicts the fact that 0 is the unique peak point.
Theorem 5. Suppose that U(ξ) is a single peak soliton solution for the B(2,2) equation (3) at the peak point ξ0 = 0. Then one has the following solutions classification and asymptotic behavior.
- (i)
If U(0) ≠ 0, then U(ξ) is a smooth soliton solution.
- (ii)
If U(0) = 0 and A = −2c2/3, then U(ξ) gives the peaked soliton solution (−2c2/3)(1 − e−|x−ct|/2).
- (iii)
If U(0) = 0 and A ≠ −2c2/3, then U(ξ) is a cusped soliton solution and
()
Proof. (i) If U(0) ≠ 0, then U(ξ) ∈ C∞(R) for any ξ ∈ R, and so U(ξ) is a smooth soliton solution.
(ii) If U(0) = 0 and A = −2c2/3, then (9) becomes
(iii) If U(0) = 0 and A ≠ −2c2/3, then by the definition of single peak soliton solution we have A ≠ 0; thus, 3U2 + (6A + 4c2)U + 3A2 + 2Ac2 does not contain the factor U. From (9), we obtain
3. Peakons, Cuspons, and Smooth Soliton Solutions
Theorem 5 gives a classification for all single peak soliton solutions for the B(2,2) equation (3). In this section, we will present all possible single peak soliton solutions. We should discuss three cases: A > −2c2/3, A = −2c2/3, and A < −2c2/3.
- (1)
α < −1.
- (2)
α = −1.
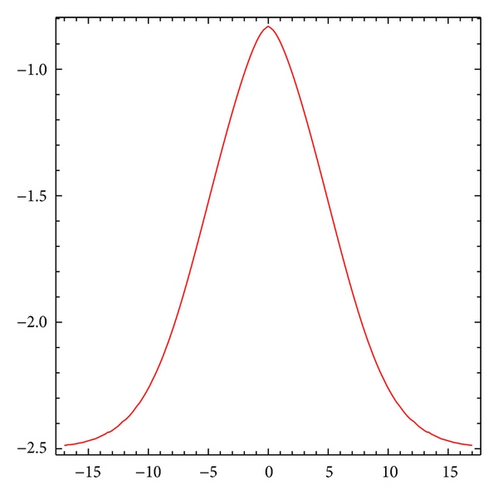
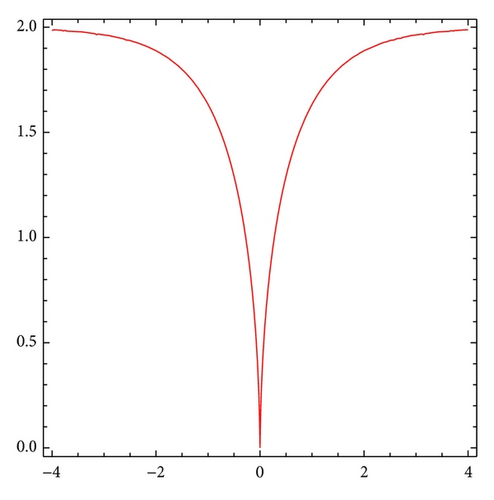
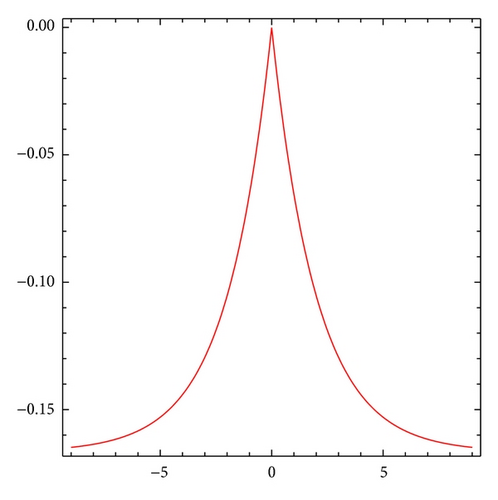
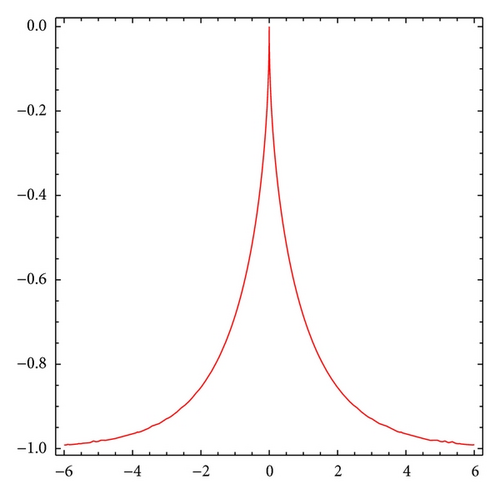
- (3)
α = 0.
- (4)
α > 0.
The profile of peaked soliton is shown in Figure 1(c).
Let us summarize our results in the following theorem.
Theorem 6. Suppose that U(x − ct) is a single peak soliton solution for the B(2,2) equation (3) at the peak point ξ0 = 0, which satisfies the inhomogeneous boundary condition (8). Then one has the following.
- (1)
For 3A + 2c2 ≠ 0, let α = A/(3A + 2c2); then
- (i)
if −1 ≤ α ≤ 0, there is no soliton for the B(2,2) equation (3);
- (ii)
if α < 0 and A < 0, the B(2,2) equation (3) has the smooth soliton solution
() -
with the following properties:
() - (iii)
if α > 0, the B(2,2) equation (3) has the cusped soliton solution
() -
with the following properties:
() - (iv)
if α < 0 and A > 0, the B(2,2) equation (3) has the cusped soliton solution
() -
with the following properties:
()
- (i)
- (2)
When 3A + 2c2 = 0, then U is the peakon
()
Acknowledgments
This work is supported by the National Natural Science Foundation of China (no. 11071222) and the Natural Science Foundation of Huzhou University (no. KX21061). The authors would like to thank the anonymous referees for their suggestions and comments which made the presentation of this work better. And the first author also wants to express her sincere gratitude to Professor Zhijun Qiao for his kind help.




