We characterize a broad class of semilinear dense range operators G_H : W → Z given by the following formula, G_Hw = Gw + H(w), w ∈ W, where Z, W are Hilbert spaces, G ∈ L(W, Z), and H : W → Z is a suitable nonlinear operator. First, we give a necessary and sufficient condition for the linear operator G to have dense range. Second, under some condition on the nonlinear term H, we prove the following statement: If , then and for all z ∈ Z there exists a sequence {w_α ∈ Z : 0 < α ≤ 1} given by w_α = G^*(αI + GG^*) ⁻¹(z − H(w_α)), such that . Finally, we apply this result to prove the approximate controllability of the following semilinear evolution equation: z^′ = Az + Bu(t) + F(t, z, u(t)), z ∈ Z, u ∈ U, t > 0, where Z, U are Hilbert spaces, A : D(A) ⊂ Z → Z is the infinitesimal generator of strongly continuous compact semigroup {T(t)} _t≥0 in Z, B ∈ L(U, Z), the control function u belongs to L²(0, τ; U), and F : [0, τ] × Z × U → Z is a suitable function. As a particular case we consider the controlled semilinear heat equation.

1. Introduction

It is well known from functional analysis that continuous linear surjective operators form an open set in the space of such operators; that is to say, if a surjective linear continuous operator is added to a linear continuous operator with a small enough norm, the resulting operator is still surjective; moreover, if a linear continuous surjective operator is perturbed by a nonlinear Lipschitz operator with a Lipschitz constant small enough, then the resulting operator is still surjective. This result is not true anymore for continuous linear operators that only have dense range; for instance, if a dense range continuous linear operator is perturbed by another linear operator with norm infinitely small, the resulting operator may not have dense range; in other words, the property of having dense range is not robust enough to be surjective. However, in this paper we proved the following statement: if a continuous linear operator with dense range is perturbed by a compact nonlinear operator with bounded range, then the resulting operator also has dense range. This result can have an unlimited number of applications, not only in the study of control theory for semilinear evolution equations, but it can also be used to find the approximate solution of functional equations in Hilbert spaces giving a formula for the error of this approximation, which is very important from the standpoint of numerical analysis. In addition, it is well known that approximate controllability is much more natural and common than exact controlabilidad, since most of the mechanical processes are diffusive, which implies that these systems can never be exactly controllable; and many years have passed to present a general result on semilinear operators with dense range to facilitate the study of the approximate controlabilidad for a large class of semilinear evolution equations whose dynamics are given by compact semigroups. However, in this work, by way of illustration, we only show how this result can be applied to study the approximate controllability of control systems governed by the semilinear heat equation.

Specifically, in this paper we characterize a broad class of semilinear dense range operators.

G_H : W → Z given by the following formula:

()

where Z, W are Hilbert spaces, G : W → Z is a bounded linear operator (continuous and linear), and H : W → Z is a suitable nonlinear operator. First, we give a necessary and sufficient condition for the linear operator G to have dense range (

). Second, we prove the following statement: If

and H is smooth enough and

is compact, then

and for all z ∈ Z there exists a sequence {w_α ∈ W : 0 < α ≤ 1} given by

()

such that

()

and the error of this approximation E_αz is given by

()

This result can be viewed as a generalization of the work done in [1–8].

We apply these results to prove the approximate controllability of the following semilinear evolution equation:

()

where Z, U are Hilbert spaces, A : D(A) ⊂ Z → Z is the infinitesimal generator of strongly continuous compact semigroup {T(t)} _t≥0 in Z, B ∈ L(U, Z), the control function u belongs to L²(0, τ; U), and F : [0, τ] × Z × U → Z is a smooth enough function.

Remark 1 (see [2]–[4].)The function F is smooth enough if

(a)
the mild solutions z(u) = z_u of (5) are unique,
(b)
the mild solutions z(u) = z_u depends continuously on u,
(c)
and if F is a Lipschitz function, then z(u) = z_u, as a function of u, is also a Lipchitz function.

As an application we consider the following example of controlled semilinear heat equation.

Example 2 (the interior controllability of the nD heat equation). The semilinear heat equation was studied in [8] where the authors prove the interior controllability of the following control system:

()

where Ω is a bounded domain in ℝ^N (N ≥ 1), z₀ ∈ L²(Ω), ω is an open nonempty subset of Ω, 1_ω denotes the characteristic function of the set ω, the distributed control u belongs to ∈L²([0, τ]; L²(Ω)), and the nonlinear function f : [0, τ] × 𝔑 × 𝔑 → 𝔑 is smooth enough and there are constants a, c ∈ 𝔑, with c ≠ −1, such that

()

where q_τ = [0, τ] × 𝔑 × 𝔑.

We note that the interior approximate controllability of the linear heat equation,

()

has been study by several authors, particularly by [9], and in a general fashion in [10].

The approximate controllability of the heat equation under nonlinear perturbation f(z) independents of t and u variables,

()

has been studied by several authors, particularly in [11–13], depending on conditions imposed to the nonlinear term f(z). For instance, in [12, 13] the approximate controllability of the system (9) is proved if f(z) is sublinear at infinity; that is,

()

Also, in the above reference, they mentioned that when f is superlinear at the infinity, the approximate controllability of the system (9) fails.

Our result can be applied also to the semilinear Ornstein-Uhlenbeck equation, the Laguerre equation, and the Jacobi equation. Specifically, in [8], the following well-known example of reaction diffusion equations is studied.

Example 3 (see [14], [15].)

(1)
The interior controllability of the semilinear Ornstein-Uhlenbeck equation
()
where u ∈ L²(0, τ; L²(𝔑^d, μ)), is the Gaussian measure in 𝔑^d, ω is an open nonempty subset of 𝔑^d, and the nonlinear function f : [0, τ] × 𝔑 × 𝔑 → 𝔑 is smooth enough and there are constants a, c ∈ 𝔑, with c ≠ −1, such that
()
where q_τ = [0, τ] × 𝔑 × 𝔑.
(2)
The interior controllability of the semilinear Laguerre equation
()
where , is the Gamma measure in , ω is an open nonempty subset of , and nonlinear function f : [0, τ] × 𝔑 × 𝔑 → 𝔑 is smooth enough and there are constant a, c ∈ 𝔑, with c ≠ −1, such that
()
where q_τ = [0, τ] × 𝔑 × 𝔑.
(3)
The interior controllability of the semilinear Jacobi equation
()
where t > 0, x ∈ [−1,1] ^d, u ∈ L²(0, τ; L²([−1,1] ^d, μ_α,β)), is the Jacobi measure in [−1,1] ^d, ω is an open nonempty subset of [−1,1] ^d, and the nonlinear function f : [0, τ] × 𝔑 × 𝔑 → 𝔑 is smooth enough and there are constants a, c ∈ 𝔑, with c ≠ −1, such that
()
where q_τ = [0, τ] × 𝔑 × 𝔑.

2. Dense Range Linear Operators

In this section we shall present a characterization of dense range bounded linear operators. To this end, we denote by L(W, Z) the space of linear and bounded operators mapping W to Z, endowed with the uniform convergence norm, and we will use the following lemma from [16] in Hilbert space.

Lemma 4. Let G^* ∈ L(Z, W) be the adjoint operator of G ∈ L(W, Z). Then the following statements hold:

(i)
Rang (G) = Z⇔∃γ > 0 such that
()
(ii)
.
The following lemma follows from Lemma 4 (ii).

Lemma 5 (see [1], [7], [8], [16]–[22].)The following statements are equivalent:

(a)
,
(b)
Ker (G^*) = {0},
(c)
〈GG^*z, z〉>0, z ≠ 0 in Z,
(d)
,
(e)
for all z ∈ Z we have Gw_α = z − α(αI + GG^*) ⁻¹z, where
()
So, lim _α→0Gw_α = z and the error E_αz of this approximation is given by the formula
()

Remark 6. Lemma 5 implies that the family of linear operators Γ_α : Z → W, defined for 0 < α ≤ 1 by

()

is an approximate inverse for the right of the operator G, in the sense that

()

in the strong topology.

Proposition 7. If the , then

()

Proof. If , then from Lemma 4(ii) we have that

()

Therefore,

()

Then, using the Cauchy Schwartz inequality, we obtain

()

which is equivalents to

()

Consequently,

()

Proposition 8. If for some β ∈ (0,1] one has that

()

then

()

Proof. Suppose that ∥β(βI + GG^*) ⁻¹∥<1. Then, from the following identity:

()

we get that

()

Since ∥β(βI + GG^*) ⁻¹∥<1, we obtain that GG^*(βI + GG^*) ⁻¹ is a homeomorphism. Consequently, Rang (GG^*(βI + GG^*) ⁻¹) = Z, which implies that Rang (G) = Z.

Corollary 9. If and Rang (G) ≠ Z, then

()

Moreover,

()

3. Dense Range Semilinear Operators

In this section we shall look for conditions under which the semilinear operator

G_H : W → Z, given by

()

has dense range.

Theorem 10. If , H is continuous, and is compact, then , and for all z ∈ Z there exists a sequence {w_α ∈ Z : 0 < α ≤ 1} given by

()

such that

()

and the error of this approximation E_αz is given by

()

Proof. For each z ∈ Z fixed we shall consider the following family of nonlinear operators K_α : W → W given by

()

First, we shall prove that for all α ∈ (0,1] the operator K_α has a fix point w_α. In fact, since H is a continuous function, the set

is compact, and G is a linear bounded operator, then there exists a constant M > 0 such that

()

Therefore, the operator K_α maps the ball B_r(0) ⊂ W of center zero and radio r ≥ ∥Γ_α∥(∥z∥+M) into itself. Hence, applying the Schauder fixed point theorem, we get that the operator K_α has a fixed point w_α ∈ B_r(0) ⊂ W.

Since is compact, without loss of generality, we can assume that the sequence H(w_α) converges to y ∈ Z as α → 0. So, if we consider

()

then,

()

Hence,

()

To conclude the proof of this theorem, it is enough to prove that

()

From Lemma 5(d) we get that

()

On the other hand, from Proposition 7 we get that

()

Therefore, since H(w_α) converges to y as α → 0, we get that

()

Consequently,

()

4. Controllability of Nonlinear Evolution Equations

In this section we shall apply the foregoing results to characterize the approximate controllability of the semilinear evolution equation

()

where Z_τ = [0, τ] × Z × U and B₁ : U → Z is a linear and bounded operator.

We observe that the controllability of semilinear systems has been studied by several authors, particularly interesting is the work done by [18–26].

Definition 11 (exact controllability). The system (48) is said to be exactly controllable on [0, τ] if for every z₀, z₁ ∈ Z there exists u ∈ L²(0, τ; U) such that the mild solution z(t) of (48) corresponding to u verifies

()

as shown in Figure 1.

Description unavailable — **Figure 1**
Open in figure viewer PowerPoint

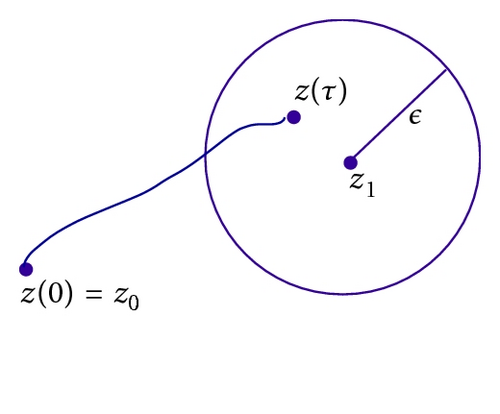
Definition 12 (approximate controllability). The system (48) is said to be approximately controllable on [0, τ] if for every z₀, z₁ ∈ Z, ε > 0 there exists u ∈ L²(0, τ; U) such that the solution z(t) of (48) corresponding to u verifies

()

as shown in Figure 2.

Definition 13 (controllability to trajectories). The system (48) is said to be controllable to trajectories on [0, τ] if for every and there exists u ∈ L²(0, τ; U) such that the mild solution z(t) of (48) corresponding to u verifies:

()

as shown in Figure 3.

Definition 14 (null controllability). The system (48) is said to be null controllable on [0, τ] if for every z₀ ∈ Z there exists u ∈ L²(0, τ; U) such that the mild solution z(t) of (48) corresponding to u verifies:

()

as shown in Figure 4.

Remark 15. It is clear that exact controllability of the system (48) implies approximate controllability, null controllability, and controllability to trajectories of the system. But, it is well known [27] that due to the diffusion effect or the compactness of the semigroup generated by −Δ, the heat equation can never be exactly controllable. We observe also that the linear case controllability to trajectories and null controllability are equivalent. Nevertheless, the approximate controllability and the null controllability are in general independent. Therefore, in this paper we will concentrated only on the study of the approximate controllability of the system (48).

Now, we shall describe the strategy of this work:

First, we characterize the approximate controllability of the auxiliary linear system

()

After that, we write the system (48) in the form

()

where G(t, z, u) = F(t, z, u) − az − cB₁u is a smooth enough and bounded function.

Finally, the approximate controllability of the system (55) follows from the controllability of (54), the compactness of the semigroup generated by the operator A, the uniform boundedness of the nonlinear term G, and applying Schauder fixed point theorem.

Remark 16. If c ≠ 1 and B = B₁, then the system z^′ = Az + Bu(t) is approximately controllable if and only if the system (55) is approximately controllable.

4.1. The Linear System

First, we shall characterize the approximate controllability of the linear system (54), and to this end, for all z₀ ∈ Z and u ∈ L²(0, τ; U) the initial value problem

()

admits only one mild solution given by

()

Definition 17. For the system (54) we define the following concept: the controllability map (for τ > 0) G_a : L²(0, τ; U) → Z is given by

()

whose adjoint operator

()

The following lemma follows from Lemma 5.

Lemma 18. Equation (54) is approximately controllable on [0, τ] if and only if one of the following statements holds:

(a)
,
(b)
,
(c)
, z ≠ 0 in Z,
(d)
,
(e)
, ∀t ∈ [0, τ], ⇒z = 0,
(f)
for all z ∈ Z one has , where
()
So, lim _α→0G_au_α = z and the error E_αz of this approximation is given by the formula
()

Remark 19. Lemma 5 implies that the family of linear operators Γ_α : Z → L²(0, τ; U), defined for 0 < α ≤ 1 by

()

is an approximate inverse for the right of the operator G_a, in the sense that

()

in the strong topology.

4.2. The Semilinear System

Now, we are ready to characterize the approximate controllability of the semilinear system (48), which is equivalent to proof of the approximate controllability of the system (55). To this end, we notice that, for all z₀ ∈ Z and u ∈ L²(0, τ; U) the initial value problem

()

admits only one mild solution given by

()

Definition 20. For the system (55) we define the following concept: the nonlinear controllability map (for τ > 0) G_g : L²(0, τ; U) → Z is given by

()

where H : L²(0, τ; U) → Z is the nonlinear operator given by

()

The following lemma is trivial.

Lemma 21. Equation (55) is approximately controllable on [0, τ] if and only if .

Definition 22. The following equation will be called the controllability equations associated to the nonlinear equation (55)

()

Now, we are ready to present a result on the approximate controllability of the semilinear evolutions equation (48).

Theorem 23. If the linear system (54) is approximately controllable, then system (55) is approximately controllable on [0, τ]. Moreover, a sequence of controls steering the system (55) from initial state z₀ to an ϵ neighborhood of the final state z₁ at time τ > 0 is given by the formula

()

and the error of this approximation E_α is given by

()

Proof. From Theorem 10, it is enough to prove that the function H given by (103) is continuous and is a compact set, which follows from the compactness of the semigroup {T(t)} _t≥0, the smoothness and the boundedness of the nonlinear term G (see [8, 27]).

So, putting z = z₁ − e^aτT(τ)z₀ and using (65), we obtain the desired result

()

5. Application to the Nonlinear Heat Equation

As an application of this result we shall prove the controllability of the semilinear nD heat equation (6). To this end, we shall use the following strategy:

first, we prove that the auxiliary linear system

()

is approximately controllable.

After that, we write the system(6) as follows:

()

where g(t, z, u) = f(t, z, u) − az − cu is a smooth and bounded function.

Then to prove the controllability of the linear equation (72), we use the classical Unique Continuation Principle for Elliptic Equations (see [28]) and the following results.

Lemma 24 (see Lemma 3.14 from [16], page 62.)Let {α_j} _j≥1 and {β_i,j : i = 1,2, …, m} _j≥1 be two sequences of real numbers such that: α₁ > α₂ > α₃⋯. Then

()

iff

()

Finally, the approximate controllability of the system (73) follows from the controllability of (72), the compactness of the semigroup generated by the Laplacean operator Δ, and the uniform boundedness of the nonlinear term g by applying Theorem 23.

5.1. Abstract Formulation of the Problem

In this part we choose a Hilbert space where system (6) can be written as an abstract differential equation; to this end, we consider the following notations.

Let us consider the Hilbert space Z = L²(Ω) and 0 = λ₁ < λ₂ < ⋯<λ_j → ∞ the eigenvalues of −Δ, each one with finite multiplicity γ_j equal to the dimension of the corresponding eigenspace. Then we have the following well-known properties.

(i)
There exists a complete orthonormal set {ϕ_j,k} of eigenvectors of A = −Δ.
(ii)
For all z ∈ D(A) we have
()
where 〈·, ·〉 is the inner product in Z and
()
So, {E_j} is a family of complete orthogonal projections in Z and .
(iii)
−A generates a compact analytic semigroup {T(t)} given by
()

Consequently, systems (6), (72), and (73) can be written, respectively, as an abstract differential equations in Z:

()

where u ∈ L²([0, τ]; U), U = Z, B_ω : U → Z, B_ωu = 1_ωu is a bounded linear operator, f^e : [0, τ] × Z × U → Z is defined by f^e(t, z, u)(x) = f(t, z(x), u(x)), ∀x ∈ Ω, and g^e(t, z, u) = f^e(t, z, u) − az − cu.

On the other hand, the hypothesis (7) implies that

()

where Z_τ = [0, τ] × Z × U. Therefore, g^e : [0, τ] × Z × U → Z is bounded and smooth enough.

5.2. The Linear Heat Equation

In this part we shall prove the interior controllability of the linear system (80). To this end, we notice that for all z₀ ∈ Z and u ∈ L²(0, τ; U) the initial value problem,

()

admits only one mild solution given by

()

Definition 25. For the system (80) we define the following concept: the controllability map (for τ > 0) G_a : L²(0, τ; U) → Z is given by

()

whose adjoint operator

is given by

()

As a consequence of Lemma 18 and (101) one can prove the following result.

Lemma 26. Equation (80) is approximately controllable on [0, τ] if and only if one of the following statements holds:

(a)
,
(b)
,
(c)
, z ≠ 0 in Z,
(d)
,
(e)
, ∀t ∈ [0, τ], ⇒z = 0,
(f)
for all z ∈ Z one has , where
()
So, lim _α→0G_au_α = z and the error E_αz of this approximation is given by
()

Theorem 27. The system (80) is approximately controllable on [0, τ]. Moreover, a sequence of controls steering the system (80) from initial state z₀ to an ϵ neighborhood of the final state z₁ at time τ > 0 is given by

()

and the error of this approximation E_α is given by

()

Proof. It is enough to show that the restriction of G_a to the space L²(0, τ; L²(ω)) has range dense; that is, or . Consequently, G_a,ω : L²(0, τ; L²(ω)) → Z takes the following form:

()

whose adjoint operator

is given by

()

To this end, we observe that

and T^*(t) = T(t). Suppose that

()

Then, since 1 + c ≠ 0, this is equivalent to

()

On the other hand,

()

Hence, from Lemma 24, we obtain that

()

Now, putting

, ∀x ∈ Ω, we obtain that

()

Then, from the classical Unique Continuation Principle for Elliptic Equations (see [28]), it follows that f(x) = 0, ∀x ∈ Ω. So,

()

On the other hand, {ϕ_j,k} is a complete orthonormal set in Z = L²(Ω), which implies that 〈z, ϕ_j,k〉 = 0. Hence, z = 0. So,

, and consequently

. Hence, the system (80) is approximately controllable on [0, τ], and the remainder of the proof follows from Lemma 26.

5.3. The Semilinear Heat Equation

In this part we shall prove the interior controllability of the semilinear nD heat equation given by (6), which is equivalent to the proof of the approximate controllability of the system (81). To this end, for all z₀ ∈ Z and u ∈ L²(0, τ; U) the initial value problem,

()

admits only one mild solution given by

()

Definition 28. For the system (81) we define the following concept: the nonlinear controllability map (for τ > 0) G_g : L²(0, τ; U) → Z is given by

()

where H : L²(0, τ; U) → Z is the nonlinear operator given by

()

The following lemma is trivial.

Lemma 29. Equation (81) is approximately controllable on [0, τ] if and only if .

Definition 30. The following equation will be called the controllability equations associated to the nonlinear equation (81):

()

Now, we are ready to present a result on the interior approximate controllability of the semilinear nD heat equation (6).

Theorem 31. The system (81) is approximately controllable on [0, τ]. Moreover, a sequence of controls steering the system (81) from initial state z₀ to an ϵ neighborhood of the final state z₁ at time τ > 0 is given by

()

and the error of this approximation E_α is given by

()

6. Conclusion

We believe that these results can be applied to a broad class of reaction diffusion equation like the following well-known systems of partial differential equations.

Example 32. The thermoelastic plate equation

()

where α ≠ 0, β > 0, Ω is a sufficiently regular bounded domain in 𝔑³, ω is an open nonempty subset of Ω, 1_ω denotes the characteristic function of the set ω, the distributed control u_i ∈ L²([0, τ]; L²(Ω)), i = 1, 2, w, θ denote the vertical deflection and the temperature of the plate, respectively, and the nonlinear terms f_i(t, z, u), i = 1,2, are smooth enough and there are constants a_i, c_i ∈ 𝔑, with c_i ≠ −1, i = 1,2, such that

()

where q_τ = [0, τ] × 𝔑 × 𝔑 × 𝔑.

Example 33. The equation modelling the damped flexible beam:

()

where α > 0, u ∈ L²([0, r]; L²[0,1]), ω is an open nonempty subset of [0,1], ϕ₀, ψ₀ ∈ L²[0,1], and nonlinear function f : [0, τ] × 𝔑 × 𝔑 → 𝔑 is smooth enough and there are constant a, c ∈ 𝔑, with c ≠ −1, such that

()

where q_τ = [0, τ] × 𝔑 × 𝔑 × 𝔑.

Example 34. The strongly damped wave equation with Dirichlet boundary conditions:

()

where Ω is a sufficiently smooth bounded domain in 𝔑^N, u ∈ L²([0, r]; L²(Ω)), ω is an open nonempty subset of Ω, ϕ₀, ψ₀ ∈ L²(Ω), and nonlinear function f : [0, τ] × 𝔑 × 𝔑 → 𝔑 is smooth enough and there are constants a, c ∈ 𝔑, with c ≠ −1, such that

()

where q_τ = [0, τ] × 𝔑 × 𝔑 × 𝔑.

Acknowledgments

This work has been supported by CDCHT-ULA-C-1796-12-05-AA and BCV.

References

1 Iturriaga E. and Leiva H., A necessary and sufficient condition for the controllability of linear systems in Hilbert spaces and applications, IMA Journal of Mathematical Control and Information. (2008) 25, no. 3, 269–280, https://doi.org/10.1093/imamci/dnm017, MR2442923, ZBL1162.93007.
10.1093/imamci/dnm017
Web of Science® Google Scholar
2 Leiva H., Exact controllability of the suspension bridge model proposed by Lazer and McKenna, Journal of Mathematical Analysis and Applications. (2005) 309, no. 2, 404–419, https://doi.org/10.1016/j.jmaa.2004.07.025, MR2154124, ZBL1142.93317.
10.1016/j.jmaa.2004.07.025
Web of Science® Google Scholar
3 Leiva H., Exact controllability of a non-linear generalized damped wave equation: application to the sine-Gordon equation, 13, Proceedings of the Electronic Journal of Differential Equations, 2005, 75–88, MR2312907, ZBL1144.34354.
Google Scholar
4 Leiva H., Exact controllability of semilinear evolution equation and applications, International Journal of Communication Systems. (2008) 1, no. 1.
Google Scholar
5 Leiva H. and Uzcategui J., Exact controllability for semilinear difference equation and application, Journal of Difference Equations and Applications. (2008) 14, no. 7, 671–679, https://doi.org/10.1080/10236190701726170, MR2431868, ZBL1146.93012.
10.1080/10236190701726170
Web of Science® Google Scholar
6 Leiva H., Appxoximate controllability of semilinear cascade systems in H = L²(Ω), International Mathematical Forum. (2012) 7, no. 57, 2797–2813.
Google Scholar
7 Leiva H., Merentes N., and Sanchez J. L., Interior controllability of the nD semilinear heat equation, African Diaspora Journal of Mathematics. (2011) 12, no. 2, 1–12, MR2847300, ZBL1243.93020.
Google Scholar
8 Leiva H., Merentes N., and Sánchez J. L., Approximate controllability of semilinear reaction diffusion equations, Mathematical Control and Related Fields. (2012) 2, no. 2, 171–182, https://doi.org/10.3934/mcrf.2012.2.171, MR2929444, ZBL1250.93032.
10.3934/mcrf.2012.2.171
Web of Science® Google Scholar
9 Zhang X., A remark on null exact controllability of the heat equation, SIAM Journal on Control and Optimization. (2001) 40, no. 1, 39–53, https://doi.org/10.1137/S0363012900371691, MR1855304, ZBL1002.93025.
10.1137/S0363012900371691
Web of Science® Google Scholar
10 Leiva H. and Quintana Y., Interior controllability of a broad class of reaction diffusion equations, Mathematical Problems in Engineering. (2009) 2009, 8, 708516, https://doi.org/10.1155/2009/708516, MR2530079, ZBL1206.93017.
10.1155/2009/708516
Web of Science® Google Scholar
11 Díaz J. I., Henry J., and Ramos A. M., On the approximate controllability of some semilinear parabolic boundary-value problems, Applied Mathematics and Optimization. (1998) 37, no. 1, 71–97, https://doi.org/10.1007/s002459900069, MR1485063, ZBL0936.93010.
10.1007/s002459900069
Web of Science® Google Scholar
12 Fernandez-Cara E., Remark on approximate and null controllability of semilinear parabolic equations, 4, Proceedings of the Controle et Equations AUX Derivees Partielles, ESAIM, 1998, 73–81.
Google Scholar
13 Fernández-Cara E. and Zuazua E., Controllability for blowing up semilinear parabolic equations, Comptes Rendus de l′Académie des Sciences I. (2000) 330, no. 3, 199–204, https://doi.org/10.1016/S0764-4442(00)00115-4, MR1748308, ZBL0952.93061.
10.1016/S0764-4442(00)00115-4
Google Scholar
14 Bárcenas D., Leiva H., and Urbina W., Controllability of the Ornstein-Uhlenbeck equation, IMA Journal of Mathematical Control and Information. (2006) 23, no. 1, 1–9, https://doi.org/10.1093/imamci/dni016, MR2212258, ZBL1106.93007.
10.1093/imamci/dni016
Web of Science® Google Scholar
15 Barcenas D., Leiva H., Quintana Y., and Urbina W., Controllability of Laguerre and Jacobi equations, International Journal of Control. (2007) 80, no. 8, 1307–1315, https://doi.org/10.1080/00207170701294581, MR2354345, ZBL1133.93007.
10.1080/00207170701294581
Web of Science® Google Scholar
16 Curtain R. F. and Pritchard A. J., Infinite Dimensional Linear Systems Theory, 1978, 8, Springer, Berlin, Germany, Lecture Notes in Control and Information Sciences, MR516812, https://doi.org/10.1007/BFb0006761, ZBL0444.60046.
10.1007/BFb0006761
Google Scholar
17 Curtain R. F. and Zwart H., An Introduction to Infinite-Dimensional Linear Systems Theory, 1995, 21, Springer, New York, NY, USA, Texts in Applied Mathematics, https://doi.org/10.1007/978-1-4612-4224-6, MR1351248, ZBL0852.93033.
10.1007/978-1-4612-4224-6
Google Scholar
18 Balachandran K., Park J. Y., and Trujillo J. J., Controllability of nonlinear fractional dynamical systems, Nonlinear Analysis: Theory, Methods & Applications. (2012) 75, no. 4, 1919–1926, https://doi.org/10.1016/j.na.2011.09.042, MR2870885.
10.1016/j.na.2011.09.042
Web of Science® Google Scholar
19 Bashirov A. E. and Mahmudov N. I., On Concepts of controllability for deterministic and stochastic systems, SIAM Journal on Control and Optimization. (1999) 37, no. 6, 1808–1821, https://doi.org/10.1137/S036301299732184X, MR1720139, ZBL0940.93013.
10.1137/S036301299732184X
Web of Science® Google Scholar
20 Dauer J. P. and Mahmudov N. I., Approximate controllability of semilinear functional equations in Hilbert spaces, Journal of Mathematical Analysis and Applications. (2002) 273, no. 2, 310–327, https://doi.org/10.1016/S0022-247X(02)00225-1, MR1932491, ZBL1017.93019.
10.1016/S0022-247X(02)00225-1
Web of Science® Google Scholar
21 Dauer J. P. and Mahmudov N. I., Controllability of some nonlinear systems in Hilbert spaces, Journal of Optimization Theory and Applications. (2004) 123, no. 2, 319–329, https://doi.org/10.1007/s10957-004-5151-3, MR2101408.
10.1007/s10957-004-5151-3
Web of Science® Google Scholar
22 Mahmudov N. I., Approximate controllability of semilinear deterministic and stochastic evolution equations in abstract spaces, SIAM Journal on Control and Optimization. (2003) 42, no. 5, 1604–1622, https://doi.org/10.1137/S0363012901391688, MR2046377, ZBL1084.93006.
10.1137/S0363012901391688
Web of Science® Google Scholar
23 de Teresa L., Approximate controllability of a semilinear heat equation in ℝ^N, SIAM Journal on Control and Optimization. (1998) 36, no. 6, 2128–2147, https://doi.org/10.1137/S036012997322042, MR1638956, ZBL0935.93011.
10.1137/S036012997322042
Web of Science® Google Scholar
24 de Teresa L. and Zuazua E., Approximate controllability of a semilinear heat equation in unbounded domains, Nonlinear Analysis: Theory, Methods & Applications. (1999) 37, no. 8, 1059–1090, https://doi.org/10.1016/S0362-546X(98)00085-6, MR1689285, ZBL0946.93006.
10.1016/S0362-546X(98)00085-6
Web of Science® Google Scholar
25 Naito K., Controllability of semilinear control systems dominated by the linear part, SIAM Journal on Control and Optimization. (1987) 25, no. 3, 715–722, https://doi.org/10.1137/0325040, MR885194, ZBL0617.93004.
10.1137/0325040
Web of Science® Google Scholar
26 Naito K., Approximate controllability for trajectories of semilinear control systems, Journal of Optimization Theory and Applications. (1989) 60, no. 1, 57–65, https://doi.org/10.1007/BF00938799, MR981945, ZBL0632.93007.
10.1007/BF00938799
Web of Science® Google Scholar
27 Barcenas D., Leiva H., and Sívoli Z., A broad class of evolution equations are approximately controllable, but never exactly controllable, IMA Journal of Mathematical Control and Information. (2005) 22, no. 3, 310–320, https://doi.org/10.1093/imamci/dni029, MR2160210, ZBL1108.93014.
10.1093/imamci/dni029
Web of Science® Google Scholar
28 Protter M. H., Unique continuation for elliptic equations, Transactions of the American Mathematical Society. (1960) 95, 81–91, MR0113030, https://doi.org/10.1090/S0002-9947-1960-0113030-3, ZBL0094.07901.
10.1090/S0002-9947-1960-0113030-3
Google Scholar

Citing Literature

All articles

A Characterization of Semilinear Dense Range Operators and Applications

Abstract

1. Introduction

2. Dense Range Linear Operators

3. Dense Range Semilinear Operators

4. Controllability of Nonlinear Evolution Equations

4.1. The Linear System

4.2. The Semilinear System

5. Application to the Nonlinear Heat Equation

5.1. Abstract Formulation of the Problem

5.2. The Linear Heat Equation

5.3. The Semilinear Heat Equation

6. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Characterization of Semilinear Dense Range Operators and Applications

Abstract

1. Introduction

2. Dense Range Linear Operators

3. Dense Range Semilinear Operators

4. Controllability of Nonlinear Evolution Equations

4.1. The Linear System

4.2. The Semilinear System

5. Application to the Nonlinear Heat Equation

5.1. Abstract Formulation of the Problem

5.2. The Linear Heat Equation

5.3. The Semilinear Heat Equation

6. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Related

Information