Volume 2013, Issue 1 725495

Research Article

Open Access

Traveling Wavefronts of Competing Pioneer and Climax Model with Nonlocal Diffusion

Xiaojing Yu,

Xiaojing Yu

School of Mathematics, South China Normal University, Guangzhou 510631, China scnu.edu.cn

Search for more papers by this author

Peixuan Weng,

Corresponding Author

Peixuan Weng

[email protected]

School of Mathematics, South China Normal University, Guangzhou 510631, China scnu.edu.cn

Search for more papers by this author

Yehui Huang,

Yehui Huang

School of Mathematics, South China Normal University, Guangzhou 510631, China scnu.edu.cn

Search for more papers by this author

Xiaojing Yu,

Xiaojing Yu

School of Mathematics, South China Normal University, Guangzhou 510631, China scnu.edu.cn

Search for more papers by this author

Peixuan Weng,

Corresponding Author

Peixuan Weng

[email protected]

School of Mathematics, South China Normal University, Guangzhou 510631, China scnu.edu.cn

Search for more papers by this author

Yehui Huang,

Yehui Huang

School of Mathematics, South China Normal University, Guangzhou 510631, China scnu.edu.cn

Search for more papers by this author

First published: 23 April 2013

https://doi.org/10.1155/2013/725495

Citations: 2

Academic Editor: Dumitru Baleanu

Share a link

Email
Wechat
Bluesky

Abstract

We study a competing pioneer-climax species model with nonlocal diffusion. By constructing a pair of upper-lower solutions and using the iterative technique, we establish the existence of traveling wavefronts connecting the pioneer-existence equilibrium and the coexistence equilibrium. We also discuss the asymptotic behavior of the wave tail for the traveling wavefronts as s = x + ct → −∞.

1. Introduction

As we know, the interactions among species are important in determining the process of evolution for the ecosystem, and the modeling accompanied with the mathematical analysis of the models can help people to understand and control the propagation of species. In general, the per capital growth rate (i.e., fitness) for a species in the model is assumed to be a function of a weighted total density of all interacting species. A well-known example is the standard Lotka-Volterra model; its fitness of a species is a linear function. It is natural to consider other kinds of fitness functions other than the linear one, because of the various species and interaction rules. In this paper, we will analyze a reaction-diffusion model describing pioneer and climax species. This model describes interaction among species with peculiar fitness functions.

A species is called a pioneer species if it thrives best at lower density but its fitness decreases monotonically with total population density for overcrowded. Thus, the fitness function of a pioneer species is assumed to be a decreasing function. Pine and yellow poplar are the species of this type. A species is called a climax species if its fitness increases up to a maximum value and then decreases of its total density. Hence, a climax population is assumed to have a nonmonotone, “one-humped” smooth fitness function. Oak and maple are the climax species.

A typical reaction-diffusion model for a pioneer-climax species is given by the following system:

()

where u and v represent densities of the pioneer and climax species, respectively. f and g denote the pioneer fitness function and climax fitness function, respectively, c_ij > 0 (i, j = 1,2). By making changes of variables

, system (1) changes into the form (the tildes of

and

are dropped out)

()

where we still use c₁₁ and c₂₂ as the new coefficients without confusing.

From the previous introduction, we assume that the pioneer fitness function f satisfies

()

for some z₀ > 0, and the climax fitness function g satisfies

()

Ricker [1] used the fitness function f(u) = e^r(1−u) − a, Hassell and Comins [2] used the fitness function f(u) = (r/(1 + bu) ^p) − a, and Cushing [3] used the fitness function g(u) = ue^r(1−u) − a. It is obvious that these f and g have the curves in Figure 1.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Typical fitness functions for pioneer species and climax species.

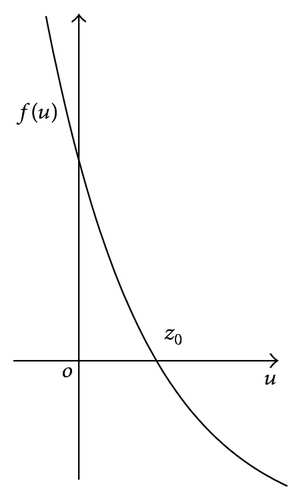
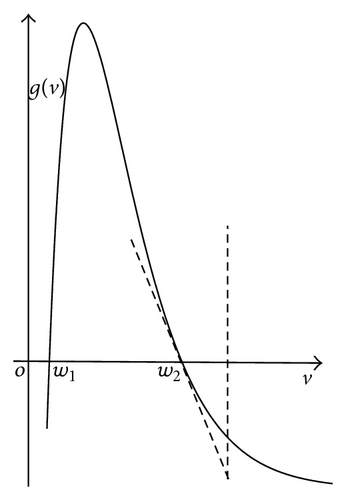
There are some existing results about the stability and traveling wave solutions for (2) ([4–6]). About traveling wave solutions, Brown et al. [4] studied the traveling wave of (1) connecting two boundary equilibria by singular perturbation technique, and Yuan and Zou [6] obtained the existence of traveling wave solutions connecting a monoculture state and a coexistence state by upper-lower solution method combined with the Schauder fixed point theorem. Also see van Vuuren [7] for the existence of traveling plane waves in a general class of competition-diffusion systems and Murray [8] for more biological description of traveling wave solutions.

For system without spatial diffusion, the model will be

()

Selgrade and Roberds [9], Sumner [10] analyzed the Hopf bifurcation of (5), and Selgrade and Namkoong [11], Sumner [12] considered the stable periodic behavior of (5). Because of the existence of rich equilibria and the various ranges of parameters, the dynamics of ordinary differential system (5) are complex, and a detailed review of all equilibrium types can be found in Buchanan [13, 14].

Although the Laplacian operator Δ : = ∂²/∂x² is always used to model the diffusion of the species, it suggests that the population at the location x can only be influenced by the variation of the population near x. As we know that the individuals can move freely, then the movement of individuals is bounded to affect the other individuals. So, the Laplacian operator may have some shortage to describe the diffusion. One way to deal with this problem is to replace the Laplacian operator with a convolution diffusion term This implies that the probability distribution function for the population at location y moving to the location x is J(x − y). At time t, the total individuals that move from the whole space into the location x will be . Therefore, one may call it as a nonlocal diffusion, and, correspondingly, call ∂²u(t, x)/∂x² as a local diffusion. During the recent years, the models with the nonlocal diffusion have been attracted much more attentions (see [15–18]).

In this paper, instead of (2), we will concentrate on the following pioneer-climax species with nonlocal diffusion:

()

where d₁, d₂ are positive constants accounting for the diffusivity, J(z) is a kernel function which is continuous on ℝ satisfying

We are interested in traveling wavefronts accounting for a mildinvasion of the two species (traveling wavefronts connecting a boundary equilibrium and the coexistence equilibrium). For system (2), the sufficient condition for (2) to have a mildinvasion is d₂/d₁ ≥ 1/2 (see [6]), but our condition in this paper for system (6) is d₂/d₁ ≥ 1, which reveals a fact that the nonlocal diffusion of either the pioneer species or the climax species did affect the climax invasion and wave propagation. Please see Section 5 for the discussion.

The remaining of this paper is organized as follows. In Section 2, there are some preliminaries about the equilibria and the system is transformed into a cooperative one. In Section 3, we prove the existence of traveling wavefronts by using an iteration scheme combined with a pair of admissible upper and lower solutions, which can be constructed obviously, and thus a criterion of the existence for traveling wavefronts is obtained. We also give a discussion on asymptotic behavior for the traveling wavefront tail as s = x + ct → −∞ in Section 4. At last, we give some concluding discussions in Section 5.

2. Preliminaries

It is evident that (0,0) is a trivial equilibrium of (6). The system (6) has at least four equilibria and at most six equilibria. The existence of nonnegative steady states depends on the locations of the three nullclines:

()

The long-term behavior of solutions to (6) can be qualitatively different caused by the different number, distribution, and types of equilibria. The dynamics of the system (6) are of course very rich and complex. However, in this paper, we will only consider the following case:

()

The condition c₁₁c₂₂ > 1 follows as a sequence. Under the previous assumption, (6) has four nontrivial equilibria: (z₀/c₁₁, 0), (0, w₁/c₂₂), (0, w₂/c₂₂), and (u^*, v^*) except for (0,0), where

()

It is obvious that u^* < z₀/c₁₁. We further assume that

()

for the technical reason. See Figure 2 for this situation.

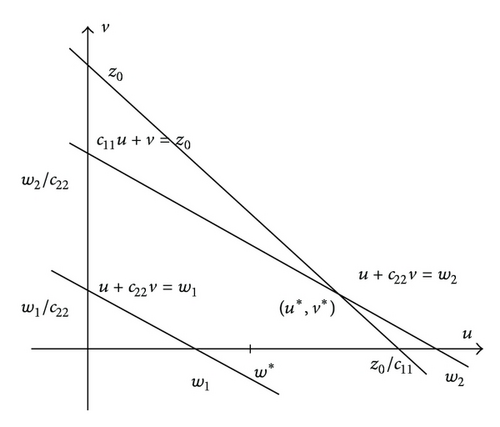
As mentioned in the introduction, we are interested in the coexistence of the two species. That means that we will seek traveling wavefronts connecting equilibrium (z₀/c₁₁, 0) and equilibrium (u^*, v^*).

By making changes of variables

and dropping the tildes, system (6) becomes

()

and the equilibria (z₀/c₁₁, 0), (u^*, v^*) are changed into (0,0), (u⁺, v⁺), respectively, where u⁺ = z₀/c₁₁ − u^*, v⁺ = v^*.

3. Existence of Traveling Wavefronts

A traveling wavefront of (6) connecting equilibria (z₀/c₁₁, 0) and (u^*, v^*) can be changed into a traveling wavefront of (11) connecting (0,0) and (u⁺, v⁺). Therefore, we consider the system (11) hereby.

A traveling wave solution of (11) is a solution with the form u(t, x) = ϕ(x + ct) = ϕ(s) and v(t, x) = φ(x + ct) = φ(s), where s = x + ct and c > 0 is a wave speed. A traveling wavefront is a traveling wave solution (ϕ(s), φ(s)) which has finite limits (ϕ(±∞), φ(±∞)). Denoting the traveling wave coordinate x + ct still by t, we derive the wave profile system from (11):

()

Associated with (12), we consider its solutions subject to the following boundary value conditions:

()

For a = (a₁, a₂), b = (b₁, b₂) ∈ ℝ², a ≤ b implies a_i ≤ b_i (i = 1,2); a < b implies a ≤ b but a ≠ b; a ≪ b implies a_i < b_i (i = 1,2). Furthermore, the norm ∥·∥ in ℝ² is the Euclidean norm. Define

()

For some constants β₁, β₂, letting b₁ = β₁ − d₁, b₂ = β₂ − d₂, we define an operator H = (H₁, H₂) : 𝔻 → C(ℝ, ℝ²) by

()

Then, (12) can be written as an equivalent form:

()

Denote Q = (Q₁, Q₂) by

()

It is obvious that a traveling wave solution of the problem (12) and (13) is a fixed point of Q and vice verse.

The following lemma states the monotone property of H.

Lemma 1. Assume that (A1) holds, for sufficiently large β₁, β₂ > 0 and (ϕ_i, φ_i) ∈ 𝔻, i = 1,2 with ϕ₁(s) ≤ ϕ₂(s) and φ₁(s) ≤ φ₂(s), s ∈ ℝ; one has

(i)
H₁(ϕ₂, φ₁)(t) ≥ H₁(ϕ₁, φ₁)(t),
H₂(ϕ₁, φ₂)(t) ≥ H₂(ϕ₁, φ₁)(t),
(ii)
H₁(ϕ₁, φ₂)(t) ≥ H₁(ϕ₁, φ₁)(t),
H₂(ϕ₂, φ₁)(t) ≥ H₂(ϕ₁, φ₁)(t)

for all t ∈ ℝ.

Proof. In order to prove (i), let f₁(x, y) = (x − z₀/c₁₁)f(z₀ − c₁₁x + y) + b₁x, g₁(x, y) = yg(z₀/c₁₁ − x + c₂₂y) + b₂y. Then

()

For 0 ≤ x ≤ u⁺, 0 ≤ y ≤ v⁺ and sufficiently large β₁, β₂ > 0, it follows that ∂f₁/∂x ≥ 0, ∂g₁/∂y ≥ 0. Thus, if ϕ₁(s) ≤ ϕ₂(s) and φ₁(s) ≤ φ₂(s) for s ∈ ℝ, we have

()

For (ii), we know that 0 ≤ ϕ₁(t) ≤ u⁺ = z₀/c₁₁ − u^* ≤ z₀/c₁₁ and f^′(y) < 0 for y ∈ ℝ. It follows that

()

From 0 ≤ φ₁(t) ≤ v⁺ = v^*, 0 ≤ ϕ₁(t) ≤ ϕ₂(t) ≤ u⁺ = z₀/c₁₁ − u^*, we have

()

Note that g^′(w) < 0 for w > w^*. This leads to

()

The proof is complete.

The conclusion of the following lemma is direct.

Lemma 2. Assume that β₁ > 0, β₂ > 0 are sufficiently large. For (ϕ, φ) ∈ 𝔻 with ϕ(t), φ(t) nondecreasing on t ∈ ℝ, H₁(ϕ, φ)(t), H₂(ϕ, φ)(t) are also nondecreasing on t ∈ ℝ.

We can easily see that Q = (Q₁, Q₂) also enjoys the same properties as those for H = (H₁, H₂) settled in Lemmas 1 and 2.

Let μ ∈ (0, min {β₁/c, β₂/c}) and

()

It is clear that (B_μ(ℝ, ℝ²), |·|_μ) is a Banach space equipped with the norm |·|_μ defined by |ϕ|_μ = sup _t∈ℝ |ϕ(t)|e^−μ|t|.

Definition 3. A pair of continuous functions , is called an upper solution and a lower solution of (12), respectively, if there exists a set Γ = {T_i ∈ ℝ, i = 1, …, k} such that and are differentiable in ℝ∖Γ and the essential bounded functions satisfy

()

for t ∈ ℝ∖Γ.

In what follows, we assume that (12) has an upper solution

and a lower solution

, such that

(P1)
for t ∈ ℝ;
(P2)
, ;
(P3)
and are nondecreasing.

Define the following profile set

()

It is obvious that

is nonempty.

For t ∈ ℝ and n ≥ 2, define

and

()

Lemma 4. For n ≥ 2, the functions , and , defined by (26) satisfy

(i)
;
(ii)
for t ∈ ℝ;
(iii)
and is a pair of upper and lower solutions of (12);
(iv)
and are continuously differentiable on t ∈ ℝ.

Proof. We only give the argument for n = 2, and the situation for n ≥ 3 can be obtained by mathematical induction. From Definition 3, we obtain

()

Let T₀ = −∞, T_k+1 = +∞. For any t ∈ ℝ, there exists some i such that t ∈ (T_i−1, T_i] (i = 1,2, ·, k) or t ∈ (T_k, ∞). We then derive

()

where i = 1, 2, …, k + 1.

By similar arguments, we can get

()

The previous arguments implies that the conclusion (ii) holds.

From the monotone property of Q, we can easily obtain that , are nondecreasing for t ∈ ℝ, and therefore the conclusion (i) holds.

For , by Lemma 1, we have

()

In a similar way, we can prove that

()

for t ∈ ℝ∖Γ. This indicates that

and

are a pair of upper and lower solutions of (12).

The conclusion (iv) is obvious. The proof is complete.

Lemma 5. , and the convergence is uniform with respect to the decay norm |·|_μ.

Proof. We have from Lemma 4 that the following limit exists:

()

It is easy to know that Λ is a closed and convex set. By the nondecreasing property of

, we have (ϕ^*(t), φ^*(t)) ∈ Λ. In the following, we prove that the convergence is uniform with respect to the decay norm.

Since

()

for any ε > 0, there exists a T = T(ε) > 0, such that for all n ≥ 1,

()

Now, we consider the sequences

for t ∈ [−T, T]. Note

is nondecreasing on t, and thus

()

, there exists a positive constant M₁, such that

for t ∈ [−T, T]. Similarly, we can prove that there exists a positive number M₂, such that

for t ∈ [−T, T].

From the previous estimates, we know that is equicontinuous on [−T, T] with respect to the supremum norm. On the other hand, we have from Lemma 4 (ii) that is uniformly bounded. By Arzéla-Ascoli theorem, there exist subsequences of which are uniformly convergent in t ∈ [−T, T]. Without loss of generality, we still express this subsequence as . Thus, there exists a positive integer N^* > 2, such that

()

Furthermore, we have

()

Summarizing the previous arguments, for n > N^* we have

()

The proof is complete.

Theorem 6. Assume that (A1) holds; if (12) has a pair of upper and lower solutions that satisfy (P1)–(P3), then the system (11) has a traveling wavefront satisfying (13).

Proof. By the Lebesgue′s dominated convergence theorem and the iteration scheme (26), we have

()

Therefore, (ϕ^*(t), φ^*(t)) is a fixed point of Q, which also satisfies (12). Furthermore, (P2) indicates that (ϕ^*(t), φ^*(t)) satisfy lim _t→−∞ (ϕ^*(t), φ^*(t)) = (0,0). On the other hand, we have from the monotonicity of (ϕ^*(t), φ^*(t)) that

exists. Furthermore, since

, we know that

. By using L’Hôspital’s rule, we obtain

()

Similarly, one can obtain

. That is,

is an equilibrium of (12). Note that the assumption (10) implies that there is only one positive equilibrium (u⁺, v⁺) of (12) satisfying (0,0) < (u, v) ≤ (u⁺, v⁺). Therefore,

and (ϕ^*(t), φ^*(t)) is a traveling wavefront satisfying (13). The proof is complete.

In order to construct a pair of admissible upper-lower solutions for (12), we linearize (12) at (0,0) and obtain

()

Thus, we consider the following characteristic equation:

()

Note that

()

The convex property of F leads to F(+∞, c) = +∞ for any c > 0. In view of the previous observation, we have the following lemma directly.

Lemma 7. The following conclusions are true.

(i)
There exists a (λ^*, c^*), λ^* > 0, c^* > 0 such that
()
(ii)
For 0 < c < c^*, F(λ, c) > 0 for λ ∈ ℝ.
(iii)
For c > c^*, the equation F(λ, c) = 0 has two zeros 0 < λ₁ < λ₂ such that
()

Now we are ready to construct the upper solution of (12).

Lemma 8. Define

()

Then for d₂ ≥ d₁,

is an upper solution of (12).

Proof. Let t₁, t₂ be such that

()

Notice that v⁺ = c₁₁u⁺, we have t₀ : = t₁ = t₂ = (1/λ₁)ln (v⁺/c₁₁).

If t < t₀, , , we have from the fact for t ∈ ℝ and w₁ < w^* ≤ u^* < z₀/c₁₁ < w₂ that

()

Similarly, we have from the fact

for t ∈ ℝ, c₁₁c₂₂ > 1 and g^′(w) < 0 for w > w^* that

()

If t > t₀, , , we have

()

The proof is complete.

Let η ∈ (1, min {2, λ₂/λ₁}) satisfying λ₁ < ηλ₁ < λ₂, we can obtain from (45) that

()

Lemma 9. Define

()

where q > 1 is a constant to be chosen later. Then

is a lower solution of (12). Furthermore,

()

is a lower solution of (12) satisfying

()

Proof. Let t₃ be such that , it follows that

()

If t < t₃ < 0, , , and for t ∈ ℝ, we have

()

Let By the fact that

()

we have

()

Note that (58) leads to

for t < t₃; it follows that

()

and thus

()

Therefore,

()

Let q > 1 sufficiently large; we can have

()

hence,

()

If t > t₃, , , and for t ∈ ℝ, we have

()

From the previous arguments, we obtain that is a lower solution of (12). By Lemma 4, we can get that is also a lower solution. Furthermore, for t < t₃, , by direct calculation, we have for t < t₃. Therefore, for t ∈ ℝ. Similarly, we have for t ∈ ℝ. The proof is complete.

Theorem 10. Assume that (A1) and d₂ ≥ d₁ hold. Then for any c ≥ c^*, the system (11) has a traveling wavefront with speed c, which connects (0,0) and (u⁺, v⁺).

Proof. The conclusion for c > c^* can be obtained from the previous discussions. We only need to establish the existence of wave fronts when c = c^*.

Let c_k ⊂ (c^*, c^* + 1) with lim _k→∞ c_k = c^*. For c_k > c^*, (12) with c = c_k admits a nondecreasing solution (ϕ_k(t), φ_k(t)) such that

()

Without loss of generality, we assume that (ϕ_k(0), φ_k(0)) = (u⁺/2, v⁺/2). Obviously, |ϕ_k(t)| ≤ u⁺, |φ_k(t)| ≤ v⁺, and ϕ_k(t), φ_k(t) satisfy

()

As the same argument in Lemma 5, we can obtain that {(ϕ_k(t), φ_k(t))} is uniformly bounded and equicontinuous on ℝ; using Arzéla-Ascoli theorem and the standard diagonal method, we can obtain a subsequence of {(ϕ_k(t), φ_k(t))}, still denoted by {(ϕ_k(t), φ_k(t))}, such that (ϕ_k(t), φ_k(t)) → (ϕ^*(t), φ^*(t)) uniformly for t in any bounded subset of ℝ, as k → ∞. Clearly, (ϕ^*(t), φ^*(t)) is nondecreasing and (ϕ^*(0), φ^*(0)) = (u⁺/2, v⁺/2).

By the dominated convergence theorem and (67), it follows that

()

Since lim _t→±∞ϕ^*(t) and lim _t→±∞φ^*(t) exist, using L’Hôspital rule leads to

()

Thus, (ϕ^*(t), φ^*(t)) is a traveling wavefront of the system (11) connecting (0,0) and (u⁺, v⁺).

Remark 11. We say that the c^* is the minimal wave speed in the sense that (11) has no traveling wavefront with c ∈ (0, c^*). We could briefly explain this in the following. In fact, the linearization of (12) at zero solution is (41), and the function F(λ, c) is obtained by substituting e^λt in the second equation of (41). For 0 < c < c^*, we know from (ii) of Lemma 7 that F(λ, c) > 0 for any λ ∈ ℝ. We have from the second equation of (12) and the second equation of (41) that (12) cannot have a solution (ϕ(t), φ(t)) that satisfies lim _t→−∞ (ϕ(t), φ(t)) = (0,0).

Theorem 12. Assume that (A1) and d₂ ≥ d₁ hold. Then for any c ≥ c^*, the system (6) has a traveling wavefront with speed c, which connects (z₀/c₁₁, 0) and (u^*, v^*).

4. Asymptotic Behavior for Traveling Wavefronts

In this section, we discuss the asymptotic behavior for the traveling wavefronts obtained in the previous section as t → −∞.

Theorem 13. Let (ϕ(t), ψ(t)) be a traveling wavefront of (11) decided by Theorem 10; then

()

where λ₁ is the smallest root of the characteristic equation (42).

Proof. Note that

()

Then we have

()

which implies that

()

Note that we have from and (A1) that

()

which is uniformly on t. By the second equation of (12), we have from (73), F(λ₁, c) = 0 and convergence theorem that

()

Since ϕ(t) = Q₁(ϕ, φ)(t), by (17), we know that

()

On the other hand, by (76), (15), (42), and (75), noting f(z₀) = 0 and using L’Hôspital’s rule, we get

()

By the first equation of (12), we have from (75) and F(λ₁, c) = 0 that

()

Combining (77) and (78), and noting that β₁ = b₁ + d₁, we obtain from a direct calculation that

()

Now, letting (ζ(t), ς(t)) be a traveling wavefront of (6) decided by Theorem 12, by the equivalence between (6) and (11), we know that (ζ(t), ς(t)) = (z₀/c₁₁ − ϕ(t), φ(t)) and thus obtain the following theorem.

Theorem 14. Let (ζ(t), ς(t)) be a traveling wavefront of (6) decided by Theorem 12; then

()

where λ₁ is the smallest root of the characteristic equation (42).

5. Concluding Discussions

We have considered a reaction model with nonlocal diffusion for competing pioneer-climax species. Some recent works (see Brown et al. [4], Yuan and Zou [6]) showed that the model with local diffusion (expressed by Laplacian operator) supports traveling wavefronts connecting two boundary equilibria or one boundary equilibrium and the coexisting equilibrium under some restrictions on the parameters. In Yuan and Zou [6], the sufficient condition for (2) to have the traveling wavefront connecting (z₀/c₁₁, 0) and (u^*, v^*) is d₂/d₁ ≥ 1/2, but ours for (6) with nonlocal diffusion is d₂/d₁ ≥ 1. For a fixed d₂, to shift d₂/d₁ ≥ 1/2 to d₂/d₁ ≥ 1, one needs a smaller d₁. But for a fixed d₁, to shift d₂/d₁ ≥ 1/2 to d₂/d₁ ≥ 1, one needs a larger d₂. These facts imply that the nonlocal diffusion of the pioneer species accelerates the mild wave propagation, while the nonlocal diffusion of the climax species defers the mild wave propagation. That is to say, the nonlocal diffusion did affect the wave propagation of these two competitive species.

The generalized boundary conditions,

()

lead to an explanation that the climax species starts its invasion after that the pioneer species has achieved its steady state, and also the competition between the two species was not intense; they can achieve a coexistence state finally. See [19] for the significance of biological invasion.

We believe that this is the first time that the dynamics of the pioneer-climax competition model with nonlocal diffusion are studied. This model has complicated equilibrium structure, and we only considered one possible case about the traveling wavefront connecting one boundary equilibrium and the coexisting equilibrium. Some other situations about the species invasions and propagation of waves would be of great interest for further research.

Acknowledgments

The authors are very grateful to the anonymous referees for careful reading and helpful suggestions which led to an improvement of their original paper. Research is supported by the Natural Science Foundation of China (11171120), the Doctoral Program of Higher Education of China (20094407110001), and the Natural Science Foundation of Guangdong Province (10151063101000003).

References

1 Ricker W. E., Stock and recruitment, Journal of the Fisheries Research Board of Canada. (1954) 11, 559–623.
10.1139/f54-039
Google Scholar
2 Hassell M. P. and Comins H. N., Discrete time models for two-species competition, Theoretical Population Biology. (1976) 9, no. 2, 202–221, MR0421737, https://doi.org/10.1016/0040-5809(76)90045-9, ZBL0338.92020.
10.1016/0040-5809(76)90045-9
CAS PubMed Web of Science® Google Scholar
3 Cushing J. M., Nonlinear matrix models and population dynamics, Natural Resource Modeling. (1988) 2, no. 4, 539–580, MR973818, ZBL0850.92069.
10.1111/j.1939-7445.1988.tb00046.x
Google Scholar
4 Brown S., Dockery J., and Pernarowski M., Traveling wave solutions of a reaction diffusion model for competing pioneer and climax species, Mathematical Biosciences. (2005) 194, no. 1, 21–36, https://doi.org/10.1016/j.mbs.2004.10.001, MR2139975, ZBL1063.92050.
10.1016/j.mbs.2004.10.001
CAS PubMed Web of Science® Google Scholar
5 Buonomo B. and Rionero S., Linear and nonlinear stability thresholds for a diffusive model of pioneer and climax species interaction, Mathematical Methods in the Applied Sciences. (2009) 32, no. 7, 811–824, https://doi.org/10.1002/mma.1068, MR2507934, ZBL1173.35350.
10.1002/mma.1068
Web of Science® Google Scholar
6 Yuan Z. and Zou X., Co-invasion waves in a reaction diffusion model for competing pioneer and climax species, Nonlinear Analysis: Real World Applications. (2010) 11, no. 1, 232–245, https://doi.org/10.1016/j.nonrwa.2008.11.003, MR2570543, ZBL1180.35159.
10.1016/j.nonrwa.2008.11.003
Web of Science® Google Scholar
7 van Vuuren J. H., The existence of travelling plane waves in a general class of competition-diffusion systems, IMA Journal of Applied Mathematics. (1995) 55, no. 2, 135–148, https://doi.org/10.1093/imamat/55.2.135, MR1358463, ZBL0841.35050.
10.1093/imamat/55.2.135
Web of Science® Google Scholar
8 Murray J. D., Mathematical Biology. I, 2002, 17, 3rd edition, Springer, New York, NY, USA, Interdisciplinary Applied Mathematics, MR1908418.
10.1007/b98868
Google Scholar
9 Selgrade J. F. and Roberds J. H., Lumped-density population models of pioneer-climax type and stability analysis of Hopf bifurcations, Mathematical Biosciences. (1996) 135, no. 1, 1–21, https://doi.org/10.1016/0025-5564(95)00109-3, MR1393845, ZBL0847.92021.
10.1016/0025-5564(95)00109-3
CAS PubMed Web of Science® Google Scholar
10 Sumner S., Hopf bifurcation in pioneer-climax competing species models, Mathematical Biosciences. (1996) 137, no. 1, 1–24, https://doi.org/10.1016/S0025-5564(96)00065-X, MR1410043, ZBL0859.92025.
10.1016/S0025-5564(96)00065-X
CAS PubMed Web of Science® Google Scholar
11 Selgrade J. F. and Namkoong G., Stable periodic behavior in a pioneer-climax model, Natural Resource Modeling. (1990) 4, no. 2, 215–227, MR1065079, ZBL0850.92060.
10.1111/j.1939-7445.1990.tb00098.x
Google Scholar
12 Sumner S., Stable periodic behavior in pioneer-climax competing species models with constant rate forcing, Natural Resource Modeling. (1998) 11, no. 2, 155–171, MR1634320.
10.1111/j.1939-7445.1998.tb00306.x
Google Scholar
13 Buchanan J. R., Asymptotic behavior of two interacting pioneer/climax species, Differential Equations with Applications to Biology (Halifax, NS, 1997), 1999, 21, American Mathematical Society, Providence, RI, USA, 51–63, Fields Institute Communications, MR1662602, ZBL0913.92026.
Google Scholar
14 Buchanan J. R., Turing instability in pioneer/climax species interactions, Mathematical Biosciences. (2005) 194, no. 2, 199–216, https://doi.org/10.1016/j.mbs.2004.10.010, MR2142488, ZBL1065.92051.
10.1016/j.mbs.2004.10.010
PubMed Web of Science® Google Scholar
15 Bates P. W., Chen X., and Chmaj A. J. J., Heteroclinic solutions of a van der Waals model with indefinite nonlocal interactions, Calculus of Variations and Partial Differential Equations. (2005) 24, no. 3, 261–281, https://doi.org/10.1007/s00526-005-0308-y, MR2174426.
10.1007/s00526-005-0308-y
Web of Science® Google Scholar
16 Chen X., Existence, uniqueness, and asymptotic stability of traveling waves in nonlocal evolution equations, Advances in Differential Equations. (1997) 2, no. 1, 125–160, MR1424765, ZBL1023.35513.
10.57262/ade/1366809230
Web of Science® Google Scholar
17 Pan S., Traveling wave fronts of delayed non-local diffusion systems without quasimonotonicity, Journal of Mathematical Analysis and Applications. (2008) 346, no. 2, 415–424, https://doi.org/10.1016/j.jmaa.2008.05.057, MR2431537, ZBL1149.35301.
10.1016/j.jmaa.2008.05.057
Web of Science® Google Scholar
18 Yu X., Wu C., and Weng P., Traveling waves for a SIRS model with nonlocal diffusion, International Journal of Biomathematics. (2012) 5, no. 5, 26, 1250036, https://doi.org/10.1142/S1793524511001787, MR2944181.
10.1142/S1793524511001787
Web of Science® Google Scholar
19 Shigesada N. and Kawasaki K., Biological Invasions: Theory and Practice, 1997, Oxford University Press, Oxford, UK.
10.1093/oso/9780198548522.001.0001
Google Scholar

All articles

Traveling Wavefronts of Competing Pioneer and Climax Model with Nonlocal Diffusion

Abstract

1. Introduction

2. Preliminaries

3. Existence of Traveling Wavefronts

4. Asymptotic Behavior for Traveling Wavefronts

5. Concluding Discussions

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Traveling Wavefronts of Competing Pioneer and Climax Model with Nonlocal Diffusion

Abstract

1. Introduction

2. Preliminaries

3. Existence of Traveling Wavefronts

4. Asymptotic Behavior for Traveling Wavefronts

5. Concluding Discussions

Acknowledgments

References

Figures

References

Related

Information